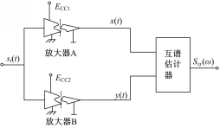
通常互谱估计需要两个相关时间序列。为了对信号进行互谱估计运算,首先要通过独立双通道放大器测量方法将其转化为互谱估计问题^{[ 5]}。图1为相互独立的双通道互谱估计器原理图。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 相互独立的双通道互谱估计器原理图Fig.1 Independent cross spectral estimator diagram

图1中,放大器A和放大器B各采用两个相互独立电源 E_CC1和 E_CC2供电,所以这两个放大器在电气上相互隔离,从而所产生的噪声也是相互独立的。设两个放大器的放大倍数分别为k₁和k₂,则两个放大器输出信号x(t)和y(t)分别为:

x(t)=k₁s_i(t)+n₁(t) (1)

y(t)=k₂s_i(t)+n₂(t) (2)

式中:n₁(t)、n₂(t)为两个相互独立的零均值观测噪声。

根据式(1)(2)能够求出x(t)和y(t)的互相关函数r_xy(τ)为:

r_xy(τ)=E{x(t)y(t+τ)} (3)

E{[k₁s_i(t)+n₁(t)][k₂s_i(t+τ)+n₂(t+τ)]}=k₁k₂r_si(τ) (4)

式中:τ为随机时间变量。

显然这种方法可以抑制放大器噪声,从而实现对信号的互谱估计。

现代互谱估计方法成立首先需要满足以下两个条件:①通过两个随机序列的线性模型可直接求得其互功率谱(互谱计算问题);②两个线性模型可通过互功率谱的分解求得(互谱分解问题)^{[ 6]}。针对互谱计算问题,有以下定理:

定理1 设时间序列x(k)、y(k)均为平稳的自回归滑动平均模型(ARMA),且联合平稳,即:

x(k)= ω_x(k) (5)

y(k)= ω_y(k) (6)

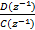
式中:

=

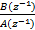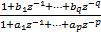(7)

=

(8)

式中:A(z^-1)、C(z^-1)的零点都处于单位圆内;ω_x(k)、ω_y(k)均为零均值白噪声;ω_x(k)、ω_y(k)的互功率谱密度为:

(ω)=σ (9)

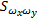
可得x(k)、y(k)的互功率谱密度为

Sxy(ω)=σ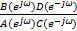

(10)

如果式(10)采用Z变换形式表示,那么可得

Sxy(z)=σ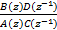

(11)

式中:σ为一个标量因子;S_xy(z)为互功率谱S_xy(ω)的Z变换,该互功率谱分解是唯一的。

关于互谱分解问题,有以下相关定义和定理:

定义1 S_xy(ω)存在且不为零,且为e^jωT的有理函数(T为采样周期),则称S_xy(ω)为有理谱。

定理2(互功率谱分解定理) 若联合平稳的两个随机过程的互功率谱S_xy(ω)具有有理谱形式,且其互相关函数r_xy(m)(m=0,1,…)均为实数,则必存在两个零极点均在单位圆内的实系数有理函数:

Hx(z-1)==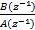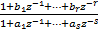

(12)

Hy(z-1)==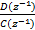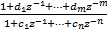

(13)

满足:

Sxy(z)=σHx(z)Hy(z-1)=σ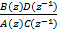

(14)

目前,很多自谱估计法都是在自相关函数的Yule-Walker方程基础上提出的,要构造互谱估计法,需先创立互相关函数的Yule-Walker方程。

定理3(互相关函数的Yule-Walker方程) 设时间序列x(k)、y(k)均为零均值、平稳且联合平稳的实AR过程,即:

x(k)=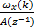

(15)

y(k)=

(16)

A(z^-1)=1+a₁z^-1+…+a_pz^-p;a_p≠0 (17)

B(z^-1)=1+b₁z^-1+…+b_qz^-q;b_q≠0 (18)

式中:A(z^-1)和B(z^-1)的根都处于单位圆内;ω_x(k)和ω_y(k)均为零均值噪声序列,且E[ω_x(k)ω_y(k+n)]=σ_xyδ(n),δ(n)为Kronecker Delta函数,则互相关函数序列r_xy(k)、r_yx(k)(k=0,1,…)满足下列Yule-Walker方程:

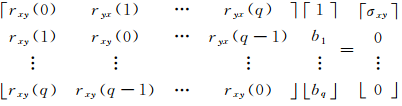(19)

简写为:

R _xy B = σ(20)

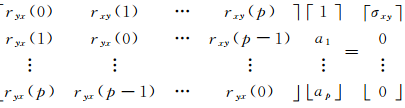(21)

简写为:

R _yx A = σ(22)

由式(20)(22)可知,求取参数 A和 B需要做矩阵求逆,运算量很大。

定理4 设矩阵 R _xy、 R _yx分别如式(19)和(21)中所定义,且 R _xy、 R _yx维数相同,则对于矩阵方程:

(23)

有:

(24)

根据定理4,可以推导出 AR模型参数估计的 Levinson算法,算法递推步骤如下。

首先初始化:

=-

(25)

=-

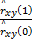(26)

= (0) + (1) (27)

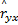
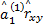
对 n=1,2,…,取:

= ( n-i+1), =1 (28)

= ( n-i+1), =1 (29)

=-

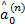
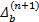
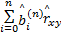
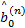
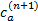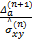(30)

=-

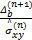(31)

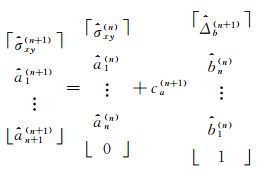(32)

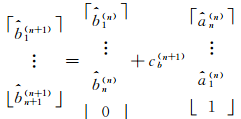(33)

由此可以计算出 σ _xy、 A和 B,进而得到时间序列 x( k)、 y( k)的互功率谱估计。

为了验证Levinson算法的谱估计性能,应用下面两个数字仿真模型:

x(k)=1.585 66x(k-1)-2.557 3x(k-2)+1.554 11x(k-3)-0.960 596x(k-4)+ω(k)+n_x(k)

y(k)=1.545 15y(k-1)-2.476 66y(k-2)+1.483 97y(k-3)-0.922 368y(k-4)+ω(k)+n_y(k)

式中:时间序列x(k)和y(k)的AR模型的极点均在单位圆附近,分别为:

[0.99 exp(±j0.9)] [0.99 exp(±j0.2)]

[0.98 exp(±j0.95)] [0.98 exp(±j0.1)]

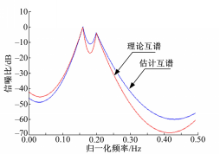
n_x(k)、n_y(k)均为测量噪声,由方差为1的ω_x(k)和ω_y(k)通过两个带通滤波器产生,取x(k)、y(k)的信噪比为0 dB,数据长度为512,Levinson算法的互谱估计图如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 Levinson算法的互谱估计Fig.2 Cross spectral estimation of the Levinson algorithm

由图2可知:在测量噪声和信噪比为0 dB的情况下,基于互谱AR模型参数估计的Levinson算法也具有良好的谱估计性能,能够有效地抑制测量噪声。

试验条件:无测量噪声和干扰,收发端一致;信噪比E _b/N₀取0,1,2,…,8 dB;随机相位范围是:e^jθ(ω)={ |θ_i(ω)∈[0, ,…, ]};信道模型是加性高斯白噪声信道选用随机二进制数作为数据源^{[ 7]}。

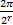
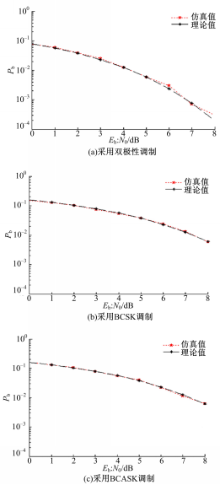
试验方法:采用9阶的m序列作为随机序列,分别选用双极性调制、二元循环移位键控(BSCK)调制和二元循环翻转移位键控(BCASK)调制。仿真结果如图3~5所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 采用不同调制方法的TDCS误码率Fig.3 The TDCS error rate under different modulation method

仿真结果表明:TDCS的误码率随着信噪比的增加而减小。采用三种调制方法得到的TDCS误码率接近理论值,其中采用BCSK和BCASK调制方法取得的效果均好于采用双极性调制方法。

试验条件:

(1)采用随机二进制数作为数据源。

(2)测量噪声ω_x(n)、ω_y(n)采用方差为1的白噪声,通过一带通滤波器生成,其表达式为:

H(z)= 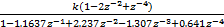其功率谱密度曲线如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 测量噪声的功率谱Fig.4 Power spectrum of the measurement noise

(3)干扰分别选用单音干扰、多音干扰、10%窄带干扰和70%窄带干扰。

(4)信噪比 E_b/ N₀=4 dB,干信比 J/E为0,1,2,…,30 dB。

(5)随机相位的范围是:

e^jθ(ω)={ 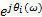|θ_i(ω)∈[0, ,…, ]}

(6)选用直接序列扩频的抗干扰性能作为比较对象。

试验方法:

(1)应用本文提出的基于互谱AR模型参数估计的Levinson算法作为信道谱估计法。

(2)采用9阶的m序列作为随机序列,周期是2⁹-1=511。

(3)调制方法分别选用双极性调制、二元循环移位键控(BSCK)调制和二元循环翻转移位键控(BCASK)调制。

仿真结果如图5~图7所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
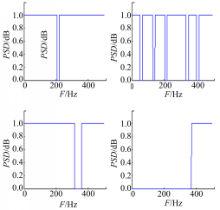
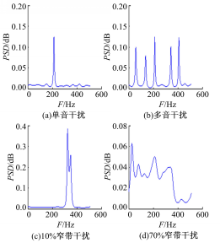	图5 基于互谱AR模型参数估计的Levinson算法在不同干扰下信道的功率谱Fig.5 Channel power spectrum under different interference of the Levinson algorithm based on the parameter estimation of cross spectral AR model

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 测量噪声背景下生成的幅度谱图Fig.6 The amplitude spectrum in the measurement of noise background

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 测量噪声背景下基于BCASK调制的不同在不同干扰下的误码率Fig.7 The TDCS error rate of different modulation in different interference in the measurement of noise background

从图5可以看出:本文提出的方法能够有效地抑制测量噪声,功率谱的分辨率也较高。从图6可以看出:应用幅度谱成型法可以很好地抑制信道中的单音干扰、多音干扰、10%窄带干扰和70%窄带干扰。从图7(a)可以看出:在有测量噪声的背景下,基于双极性调制的TDCS在不同干扰下的误码率与理论值非常接近,后期随着信噪比增加,虽然误码率有所增加,但整体上远低于理论最小误码率。从图7(b)可以看出:在有测量噪声的背景下,基于BCSK调制的TDCS在不同干扰下的误码率前期与理论值非常接近,后期对10%的窄带干扰随信噪比的增大而增加,误码率明显增加,但对其他干扰仍非常接近理论值。从图7(c)可以看出:在有测量噪声的背景下,基于BCASK调制在不同干扰下的误码率前期与理论值非常接近,后期对单音干扰随信噪比的增大而增加,误码率有明显增加,对于其他干扰仍非常接近理论值。

由以上结果可知,在有测量噪声的背景下,本文提出的基于互谱AR模型参数估计的Levinson算法的TDCS能够有效地抑制测量噪声,而且TDCS有很强的抗干扰能力,同直接序列扩频相比,大大降低了误码率。