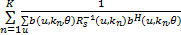杨巍(1983),女,博士研究生.研究方向:阵列信号处理.E-mail:weiyang09@mails.jlu.edu.cn
利用分数傅里叶变换(Fractional Fourier transform,FRFT)时频面旋转的特性,将Chirp信号的能量集中,并在分数阶傅里叶域内接收含宽带Chirp信号参数的方向矩阵,然后再通过窄带DOA(Direction of arrival)算法进行波达方向角估计。理论分析和仿真试验证明了该算法的有效性,并且很大程度地提高了信噪比。
We consider the problem of estimating the Directions of Arrival (DOA) of broadband Chirp signal sources using a sensor array. Since the Fractional Fourier Transform (FRFT) can rotate the time-frequency plane, the frequencies of Chirp signals are concentrated by a properly chosen rotational angle, and the direction array is also obtained in FRFT domain. By this way, the broadband DOAs estimation is then successfully processed using the well existing narrowband DOA estimation algorithms. Simulation results demonstrate that the proposed method is quite simple and has much better performance compared to the methods such as the Coherent Signal Subspace method.
Chirp信号是比较典型的非平稳信号,宽带Chirp信号的波达方向角(Direction of arrival,DOA)估计一直都是研究的热点。宽带DOA在应用时常常面临着与中心频率和瞬时频率相关的问题。为了解决这一问题,相干信号子空间法(Coherent signal subspace method,CSSM)[ 1, 2, 3]提出了聚焦矩阵和聚焦频率的概念,然后通过窄带DOA进行波达方向角估计。该算法中初始角度的选取影响CSSM的估计能力。为了提高CSSM算法的估计精度,Valaee和Kabal提出了双边相关变换(Two-sided correction transform)[ 4, 5],该算法通过计算出每个频率的噪声功率和使用无噪声的相关矩阵估计到达角,并且在聚焦频率搜索时最大限度地减少空间拟合误差。而在计算无噪声的相关矩阵时,该算法需要预先估计信源数,才能最大限度地减少错误[ 6, 7, 8]。因此需要一种可以减少预估计和提高信噪比的算法。
本文提出了一种基于分数阶傅里叶变换(Fractional Fourier transform,FRFT)的方向角估计方法。这种算法根据信号和FRFT的旋转角度确定方向矩阵,并应用窄带DOA估计方法估计波达方向角。该算法可以减少预估计,并提高信噪比。
分数阶傅里叶变换的定义形式可以解释为对时频面的旋转,这非常利于Chirp信号的分析。首先FRFT[ 9, 10, 11]的表示式为:
F α( u)= 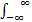
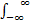
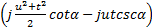
式中: A α= 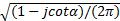
假设 M个间隔为 d的均匀线阵接收 Chirp信号,参考点接收的 Chirp信号 s( t)的表达式为:
s0( t)=exp[ jπ(2 f0 t2 +kt)] (2)
式中: f0、 k分别为 Chirp信号的初始频率和调频斜率。
对式(2)进行 FRFT,得到:
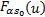 =ρ·exp =ρ·exp 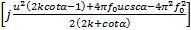 | (3) |
式中: ρ= 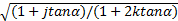
相对于参考阵元,对第 m个阵元接受的 Chi rp信号 x m( t)进行 FRFT,则有:
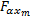

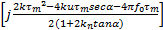
式中: τ m为 Chirp信号到达第 m个阵元时相对参考阵元的时延, τ m =mdsin θ/c, θ为 Chirp信号的入射方向角, c为速度; F αnoise( u)为加性高斯白噪声 n( t)的 FRFT变换式, n( t)的均值为零。
从式(4)可以得出阵列流形为:
b( u, α, θ)=
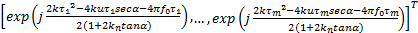 | (5) |
x( u, α)= B( u, α) s( u, α)+ n( u, α) (6)
式中: s( u, α)、 n( u, α)分别为信号和噪声的 FRFT向量。
s( u, α)=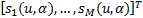 | (7) |
n( u, α)=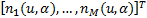 | (8) |
在 FRFT域内,得到的 FRFT矩阵表示为:
B( u, α)= | (9) |
式(4)的数学期望表示为:
E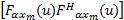 | (10) |
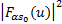
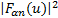
式中:
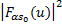 = = 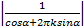 | (11) |
在波达方向角估计中,FRFT的协方差矩阵为:
R x( u) =E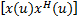 | (12) |
式(12)中第(i,j)元素为:
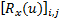 =E =E 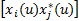 | (13) |
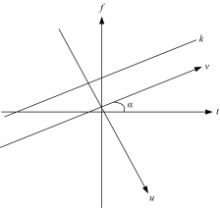
为了使Chirp信号能量在FRFT域集中,从式(11)可以得到: cotα=-k(14) 为了更直观,利用图1表示新时频轴与原时频轴的关系。
Chirp信号的斜率是计算频率集得到的,这使误差大大降低,而且在DOA估计前也无需预估计。将式(14)代入式(5)可以得到:
b(u,α,θ)=[ exp[j( cotατ1+2ku secα+2 πf0)τ1],…, exp[j( cotατm+2ku secα+2πf0)τm]] Τ (15)
通过式(15)可以看出:二维搜索降低为一维搜索,大大降低了运算量。
本文中,利用分数傅里叶变换提出的宽带Chirp信号到达角估计方法,同样可以应用到发射不同斜率的宽带Chirp信号。同一信源发射多个Chirp信号,只需检测其中一个Chirp信号的斜率,并决定旋转角度,就可得到该信源的波达方向角。该算法的优势主要表现在两个方面:①与其他算法相比较无需预估计,如信源数;②在FRFT域内Chirp信号的能量集中,远远大于噪声能量,提高了信噪比。
假设在水下5个阵元的均匀线阵接收两个信源发送的传播速度为1500 m/s[ 14]的 Chirp信号,信源分别位于-20 °和40 °,快拍数为2048。设阵元噪声的方差为 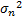
SNR=20log10 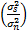
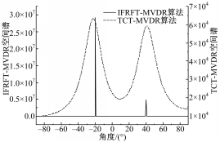
来自两个信源的 Chirp信号频率分别为1 Hz~1 kHz和1 Hz~0 .8 kHz。图2为 IFRFT-MVDR和 TCT-MVDR算法的试验结果。图中左侧纵轴代表 IFRFT-MVDR空间谱;右侧纵轴代表 TCT-MVDR空间谱。从纵轴可以看出: IFRFT-MVDR的数量级远远高于 TCT-MVDR。从图2中可以看出: IFRFT-MVDR峰值比较尖锐,分辨率高。
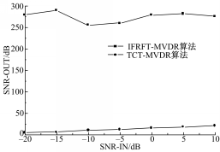
在相同的情况下,做100次Monte Carlo试验观测输入输出信噪比比率。在FRFT域内,噪声分量为| F αn( u) |2,则:
SNRout=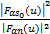 | (18) |
式中:| 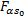
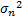
根据 Chirp信号的斜率选择旋转角度,提出了宽带 Chirp信号的 DOA估计。同时角度的选取将二维估计降到一维估计,至此将宽带估计问题变成窄带估计问题,相应的窄带算法也可以应用到 DOA估计中。并且此算法使 Chirp信号的能量比时频面 Chirp信号的能量集中,大大提高了估计精度和信噪比。试验结果证明了该算法的有效性。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| 11 |
|
| [12] |
|
| [13] |
|
| [14] |
|