引用本文
查长军, 韦穗, 杨海蓉, 丁大为. 基于稀疏表示的多类融合样本中特定目标识别. 2014, 44(3): 822-827
ZHA Chang-jun, WEI Sui, YANG Hai-rong, DING Da-wei. Special object recognition based on sparse representation in multiclass fusion sample. 吉林大学学报(工学版), 2014, 44(3): 822-827  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于稀疏表示的多类融合样本中特定目标识别
查长军1,2, 韦穗1, 杨海蓉3, 丁大为1
1.安徽大学 计算智能与信号处理教育部重点实验室,合肥 230039
2.合肥学院 机器视觉与智能控制技术重点实验室,合肥 230601
3.合肥师范学院 数学系,合肥 230061
韦穗(1946),女,教授,博士生导师.研究方向:压缩感知,图像处理与三维全息显示.E-mail:swei@ahu.edu.cn

查长军(1980),男,博士研究生.研究方向:光学成像与信号处理.E-mail:zcj_longman@sina.com

基金:NSFC-广东联合基金项目(U1201255); 高等学校博士学科点专项科研基金项目(20113401130001); 国家自然科学青年基金项目(61201227); 安徽省自然科学基金青年项目(1208085QF114); 安徽省高校省级自然科学一般项目(KJ2011B131,KJ2013B224);
摘要

针对WSN及轮廓检测系统的特点,给出了一种基于WSN的数据处理方法。该方法首先通过主分量分析提取样本特征,然后采用叠加方式对不同样本的特征进行融合,给出数学模型;并以此模型为基础,提出一种新的基于稀疏表示的多类融合样本中特定目标识别算法,该算法根据超完备字典下主要非零系数的分布情况识别出特定目标;数值仿真与实验结果验证了本文算法的有效性,综合性能优于传统方法。

关键词: 信息处理技术; 无线传感器网络; 稀疏表示; 轮廓识别; 无人值守地面传感器
中图分类号:TN911.74 文献标志码:A 文章编号:1671-5497(2014)03-0822-06
Special object recognition based on sparse representation in multiclass fusion sample
ZHA Chang-jun1,2, WEI Sui1, YANG Hai-rong3, DING Da-wei1
1. Key Laboratory of Intelligent Computing and Signal Processing, Ministry of Education, Anhui University, Hefei 230039,China
2. Key Laboratory of Machine Vision and Intelligence Control Technology, Hefei University, Hefei 230601,China
3. Department of Mathematics, Hefei Normal University,Hefei 230061,China
Fund:
Abstract

According to the characteristics of Wireless Sensor Network (WSN) and the profile detecting system, a data processing method based on WSN is proposed. In this method, first, the sample features are extracted by principal component analysis; then, the features of different samples were fused using accumulate mode. A mathematical model was given and on the basis of this model, a novel algorithm of special object recognition based on sparse representation in multiclass fusion sample was proposed. This algorithm recognizes the special target according to distribution of the main non-zero coefficients under an over-complete dictionary. Numerical simulation and experimental results demonstrate the effectiveness of the proposed algorithm, the comprehensive performance is better than the traditional methods.

Keyword: information processing; wireless sensor network; sparse representation; profiling recognition; unattended ground sensor
0 引言

一般而言,跨越边境和特定监控区的除了动物就是人,利用人和动物外形轮廓存在较大差异的特征实现对特定目标(人)的识别与监控已证明切实可行[ 1, 2, 3];但这些研究更多的是关注物体轮廓样本的获取及采用传统的方法进行识别,如:K最近邻(K-nearest neighbor classifier,KNN)、支持向量机(Support vector machines,SVM)等[ 4, 5, 6];并没有进一步探讨构成无线传感器网络(Wireless sensor network,WSN)所涉及的数据融合、降低传输数据量等问题。

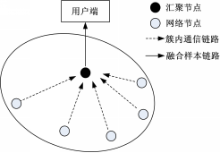
本文的主要工作是将前期研究中的轮廓检测系统作为网络节点[ 7],构成一个WSN;网络中汇聚节点接收各网络节点发送过来的样本特征向量后,对样本特征向量进行融合,然后将融合后样本发送给用户端;在用户端采用本文算法对融合样本进行识别,以判断该区域是否有特定目标(人)经过。

为了尽可能地减少WSN中传输的数据量、降低数据融合复杂度,本文给出了一种较简单的数据处理方法及其融合模型;由于该模型下的融合样本中包含多个类别的有效样本,采用经典的稀疏表示分类(Sparse representation-based classification,SRC)算法[ 8, 9, 10]并不能准确地判别样本中是否存在某一个或多个类别。针对这一不足,本文提出了一种基于稀疏表示的多类别融合样本中特定目标识别算法;与SRC方法不同的是,该算法是利用稀疏表示系数向量中主要非零系数的分布情况,识别出融合样本中特定目标;实验验证了该算法的有效性。

1 样本特征提取与数据融合
1.1 特征提取

根据文献[ 7]可知,作为WSN中网络节点的轮廓检测系统,每次采集到的物体轮廓样本信号 P是大小为 S×L的矩阵;但由于每个样本矩阵的列数 L不同,且存在很大的冗余信息;如果将该矩阵信号通过网络直接发送出去,不仅数据量较大、浪费网络资源,而且由于矩阵维数不同,不便于数据处理。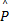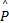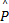为了解决以上问题,本文采用主分量分析( Principle component analysis, PCA)[11 - 12]对样本数据进行预处理,具体过程如下: ①输入:采集到的物体轮廓样本 P∈ R S×L; ②计算协方差矩阵:令 X= PT∈ R L×S,计算协方差矩阵 C XX =E[( X -E( X))( XT -E( XT))]; ③求解特征值和特征向量:采取任意方法求解 C XX的特征值 λ1, λ2,…, λ L和相应的特征向量 μ1, μ2,…, μ L; ④构造变换矩阵:按照从大到小顺序排列,选取前 k( k≤ L)个较大特征值(即: λ1≥ λ2≥…≥ λ k)所对应的特征向量构造变换矩阵 U∈ R L×k,即: U=[ μ1, μ2,…, μ k]; ⑤降维处理:利用变换矩阵 U对原始样本 P进行变换,得到变换后矩阵为 ∈ R k×S,即: = UT X= UT PT; ⑥矩阵向量化:将矩阵 所有列排成一列,并归一化得到向量 p∈ R c( c=k×S)。

通过预处理后,将得到的归一化向量 p作为样本的特征向量,发送到汇聚节点进行数据融合。

1.2 数据融合

假设 WSN中含有 N个网络节点,第 j个网络节点采集到物体轮廓样本为 Z j∈ 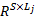(1≤ j≤ N);在本地通过预处理提取到的样本特征向量表示为 y j∈ R c(1≤ j≤ N);汇聚节点收到各网络节点的特征向量后进行数据融合,如图1所示。为降低数据融合过程中的计算复杂度,本文采取叠加方式实现融合,得到融合后样本为 r,即:

r= y1+ y2+…+ y N= 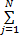y j (1)

图1 数据融合示意图Fig.1 Schematic diagram of data fusion

若考虑到各网络节点的信号发射功率、传输信道衰落以及噪声干扰等因素,式(1)可改写为:

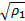
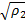
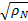
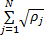
r=( α1 y1+ α2 y2+…+ α N y N)+ n= α j y j+ n(2)

式中: r∈ R c;参数 ρ j和 α j(1≤ j≤ N)分别为第 j个网络节点信号发射功率和传输路径的链路增益; n为加性高斯白噪声。当各网络节点样本特征向量维数较大时,若需要进一步降低传输数据的数据量,可通过测量矩阵 A∈ R d×c( d<c)将样本特征信息投影到低维空间,由此进一步得到融合样本数学模型:

= α j Ay j+ n= α j + n(3)

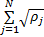
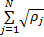
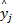
式中: 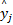= Ay j∈ R d 。

2 稀疏性分析与字典构造

为了便于分析融合后样本的稀疏性,假设融合样本 r由两个不同类别的样本特征向量 y1和 y2组成,即:

r= y1+ y2(4)

进一步,假设 x1和 x2分别为样本特征向量 y1和 y2在超完备字典 A1和 A2下的稀疏表示系数,则:

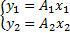(5)

结合式(4)得到:

r= y1+ y2= A1 x1+ A2 x2=[ A1, A2] 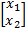= A a x a (6)

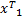
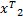
式中: A a=[ A1, A2]; x a=[ , ]T。

从式(6)中可以看出融合后样本 r在字典 A a下能够稀疏表示,且可通过计算以下最小化问题估计系数[ 13],即:

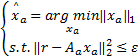(7)

式中:参数ε为允许误差。

同理,当融合样本 r由 k个类别的样本特征向量叠加而成时,同样能够稀疏表示,此时超完备字典应为 A a=[ A1, A2,…, A k], A j(1≤ j≤ k)表示第 j类特征样本字典。

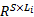
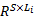
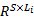
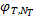
根据稀疏表示理论可知,要想稀疏表示融合后样本,则需要构造一个有效的超完备字典[14 - 15]。由于通过训练样本构造字典相对灵活,故本文采用这种方式[ 7]。假设有 T类训练样本,每类训练样本数为 N1, N2,…, N T,第 j(1≤ j≤ T)类中第 i(1≤ i≤ N j)个训练样本表示为 P j, i∈ ,则构造字典的具体步骤如下:①输入:训练样本 P j, i∈ ;②构造原子:对所有的训练样本 P j, i∈ 进行预处理,将处理后得到的样本特征向量 φ j, i∈ R c( c=S×k)作为字典原子;③构造字典:将所有原子按列组合在一起得到的矩阵即为字典: A a=[ φ1,1, φ1,2,…, ]∈ R c×n( c<n),其中: n=N1 +N2+… +N T。

3 多类融合样本中特定目标识别

通过以上稀疏性分析可知,当融合样本中存在某一类别特征样本时,通过 l1模最小化问题求解得到的稀疏系数向量中主要非零系数就分布在对应类别的原子上,而其他类别原子上的系数为零或很小;如果融合样本中包含多个类别,稀疏系数向量中的主要非零系数就分布在这几个类别原子上。

基于这一特征,本文提出了一种多类别融合样本中特定目标识别算法,该算法流程如下:

(1)输入:字典 A a∈ R c×n和融合样本 r∈ R c,其中: r由式(2)得到。

(2)稀疏表示:利用正交匹配追踪算法求解式(7)最小化问题,得到融合样本 r在字典 A a下的估计系数向量 。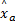

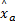
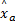
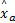
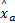
(3)计算系数向量 中分布于各类别的系数 l1模: s j=‖ δ j( )‖1,其中:1≤ j≤ T, δ j( )表示系数向量 中分布在第 j类所有原子上的系数。

(4)多类判别准则:满足以下条件判为融合样本中包含此类,即: s j /‖ ‖1≥ τ,其中: τ∈[0,1]阈值。

(5)特定目标检测输出:根据步骤(4)多类别判别结果,检测是否包含特定目标类别。

4 实验仿真与结果分析

本文实验是基于轮廓检测系统,该系统采用 S=16个开关式光电传感器 E3 F-R2 NK组成信号感知单元,传感器有效作用距离为2 m。轮廓检测系统在自然环境下主要收集了人(包括:单人和双人)、单人蹲下经过及动物(狗)三类物体轮廓样本进行训练与测试;每类训练样本数各为50,总数为150;测试样本数各为47,一共有141个样本。对所有样本进行预处理时,将样本维数为16 ×L(L为变量)的矩阵投影到维数为16 ×1的空间。

在以下实验中,融合样本由人和动物(狗)两类组成,并将人作为特定目标。在不同的实验条件下,能够判断出融合样本中存在特定目标(人)视为正确识别。实验循环测试20次,取其平均值作为该条件下的识别率或虚警率。

为了便于分析与比较,假设各网络节点的信号发射功率相同,信道链路增益为常数1,并与传统的最近邻( Nearest neighbor clas sifier, NN)[ 16]、 KNN、 SVM 和 SRC方法进行了性能比较。实验软硬件配置:操作系统为 Windows XP;仿真软件为 Matlab( R2009 a); CPU为3.4 GHz;内存为1.92 GB。

实验一 验证融合后样本的稀疏性

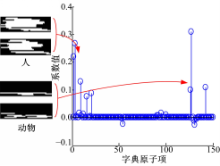
假设 WSN在某一个时段内有4个网络节点检测到物体经过,其中:2个节点为单人;2个节点为动物(狗)。各节点在本地提取样本特征信息后进行数据融合,对融合后样本进行稀疏表示,求解得到的稀疏表示系数分布如图2所示。

图2 融合样本系数分布Fig.2 Coefficients distribution of fusion sample

从图2可以看到,融合样本通过字典得到的系数仍然稀疏,且主要的非零系数分布在人和动物两个类别原子项上,而其他类别(即单人蹲下经过)上的系数几乎都为零。

该实验结果表明:由多个类别融合得到的样本在字典下能够稀疏表示;根据系数向量中主要非零系数的分布情况能够判别出融合样本中的类别组合,进而可判断存在特定目标(人)。

实验二 验证信噪比(SNR)一定时,检测到动物的节点数与识别率的关系

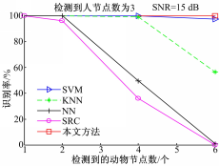
假设在某一时间段内检测到人的节点数为3,检测到动物的节点数分别为1、2、4、6,实验仿真结果如图3所示。

对于待识别的特定目标(人),受到的干扰随着检测到的动物的节点数的增加而变大;从图3中可以看到,传统的NN、KNN和SRC方法的识别率下降明显,本文方法与SVM方法基本无下降;当检测到的动物的节点数增加到6个时,本文方法识别率几乎达到100%,略高于SVM方法,表现出良好的鲁棒性。

图3 检测到动物节点数与识别率的关系Fig.3 Relationship between node number of detection animal and recognition rate

实验三 验证信噪比与识别率的关系

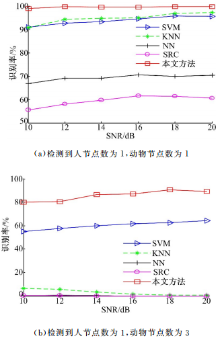
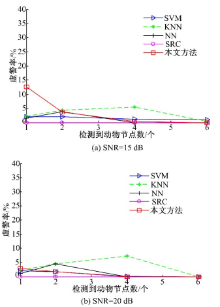
对于WSN来说,在保证需求的前提下,降低信号的发射功率可以有效地延长网络生存时间。本实验假设检测到人和动物的节点数一定,分析不同信噪比对识别性能的影响,仿真实验结果如图4所示。

图4 信噪比与识别率的关系Fig.4 Relationship between SNR and recognition rate

从图4(a)中可以看到,当检测到动物的节点数为1个时,随着信噪比的增加,本文方法识别率趋于100%;当动物节点数为3个时,尽管各方法识别率都有所下降,但本文方法仍优于传统识别方法,且随着信噪比的增加,识别性能有所改善;而传统的NN、KNN和SRC方法识别率几乎为零。

该实验结果表明:通过适当地增大节点发射功率、提高信噪比,能够有效地改善本文方法的识别性能;在一定程度上弥补其他类别样本的影响。

实验四 验证检测到的动物节点数与虚警率的关系

对于边境或特定监控区域来说,在很长的一段时间内可能只有动物而无人经过,因此能够正确判断无人经过、降低系统虚警率就显得非常重要。仿真实验结果如图5所示。

图5 检测到动物的节点数与虚警率的关系Fig.5 Relationship between node number of detection animal and recognition rate

从图5(a)中可以看到,当信噪比为15 dB时,本文方法虚警率略大于SRC方法,但随着检测到动物节点数的增加,融合样本中动物类别信息也就有所增加,这就降低了虚警的可能,因此本文方法虚警率能逐渐与SRC方法趋于一致;当信噪比增大为20 dB时,本文方法虚警率能明显得到改善,接近零虚警。

该实验结果表明:①随着检测到动物节点数的增加,融合样本中有用信息也随之增大,有利于降低本文方法的虚警率;②当检测到的动物节点数一定时,网络节点通过增大信号发射功率、提高信噪比,可以有效降低虚警率。

综上分析:传统的NN、KNN 、SVM和SRC识别方法,主要是针对单一类别的有效测试样本进行识别,当样本由多个类别融合而成时,融合样本中其他类别相对来说就是一个干扰,从而影响它们的正确识别率;而本文方法是基于稀疏表示理论,当样本由多个类别组成时,通过稀疏表示可以有效地将多类融合样本在稀疏域分离开来,进而根据系数分布情况可以判断出融合样本中类别组合,检测出特定目标。实验结果验证了本文方法的有效性。

5 结束语

针对轮廓检测系统特点,结合WSN及稀疏表示理论,给出了以轮廓检测系统为网络节点的数据处理方法及其数学模型,并以此为基础提出了一种基于稀疏表示的多类融合样本中特定目标的识别算法。仿真实验结果表明:与传统方法相比,本文方法在多方面具有更好的性能;而且在实际应用中,可以根据需要调整系统参数(如网络节点发射功率等)以满足实际需求;但对采用何种易于实现的测量矩阵将信号投影到低维空间等问题,在今后的工作中需要进一步探讨。

The authors have declared that no competing interests exist.

参考文献
[1] Russomanno David J, Chari Srikan, Emmanuel Kenny, et al. Testing and evaluation of profiling sensors for perimeter security[J]. ITEA, 2010, 31(1): 121-130. [本文引用:1] [JCR: 0.349]
[2] Sartain Ronald B, Aliberti Keith, Alexand er Troy, et al. Long-wave infrared profile feature extractor (PFx) sensor[C]∥Proc of SPIE, Unattended Ground, Sea, and Air Sensor Technologies and Applications XI, Orland o, FL, 2009. [本文引用:1]
[3] Russomanno David J, Chari Srikant, Jacobs Eddie L, et al. Near-IR sparse detector sensor for intelligent electronic fence applications[J]. IEEE Sensors Journal, 2010, 10(6): 1106-1107. [本文引用:1] [JCR: 1.475]
[4] Chari Srikant, Halford Carl, Jacobs Eddie, et al. Classification of humans and animals using an infrared profiling sensor[C]∥Proc of SPIE, Unattended Ground, Sea, and Air Sensor Technologies and Applications XI, Orland o, FL, 2009. [本文引用:1]
[5] Russomanno David, Chari Srikan, Halford Carl. Sparse detector imaging sensor with two-class silhouette classification[J]. Sensors, 2008(8): 7996-8015. [本文引用:1] [JCR: 1.953]
[6] Reynolds R K, Chari S, Russomanno D J. Embedded real-time classifier for profiling sensors and custom detector configuration[C]∥Proc of SPIE, Ground/Air Multisensor Interoperability, Integration, and Networking for Persistent ISR II, 2011. [本文引用:1]
[7] 查长军, 孙南, 张成, 等. 基于稀疏表示的特定目标识别[J]. 吉林大学学报: 工学版, 2013, 43(1): 256-260.
Zha Chang-jun, Sun Nan, Zhang Cheng, et al. Special object recognition based on sparse representation[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(1): 256-260. [本文引用:3] [CJCR: 0.701]
[8] Chen S, Donoho D, Saunders M. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129-159. [本文引用:1] [JCR: 5.952]
[9] Li Yu-long, Feng Ju-fu. Sparse represention shape model[C]∥Proceedings of 2010 IEEE 17th ICIP, 2010: 2733-2736. [本文引用:1]
[10] Wright John, Yang Allen Y, Ganesh Arvind, et al. Robust face recognition via sparse representation[J]. IEEE Transactions, PAMI, 2009, 31(2): 1-18. [本文引用:1]
[11] Yang Jian, Zhang David, Frangi Alejand ro F, et al. Two-dimensional PCA: a new approach to appearance-based face representation and recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(1): 131-137. [本文引用:1] [JCR: 4.795]
[12] Russomanno D, Yeasin M, Jacobs E, et al. Sparse detector sensor: profiling experiments for broad-scale classification[C]∥Proc of SPIE, Unattended Ground, Sea, and Air Sensor Technologies and Applications XI, Orland o, FL, 2008. [本文引用:1]
[13] Donoho D L, Elad M, Temlyakov V N. Stable recovery of sparse overcomplete representations in the presence of noise[J]. IEEE Transactions on Information Theory, 2006, 52(1): 6-18. [本文引用:1] [JCR: 2.621]
[14] Rubinstein R, Bruckstein A M, Elad M. Dictionaries for sparse representation modeling[J]. Proceedings of the IEEE, 2010, 98(6): 1045-1057. [本文引用:1] [JCR: 6.911]
[15] Smith Leslie N, Elad Michael. Improving dictionary learning: multiple dictionary updates and coefficient reuse[J]. IEEE Signal Processing Letters, 2013, 20(1): 79-82. [本文引用:1] [JCR: 1.674]
[16] Hastie Trevor, Tibshirani Robert, Friedman Jerome. The Elements of Statistical Learning[M]. New York: Springer-Verlag, 2001: 14-18. [本文引用:1]