基于特征加权模块双方向二维主成分分析的人脸识别

引用本文

顾播宇, 孙俊喜, 李洪祚, 刘红喜, 刘广文. 基于特征加权模块双方向二维主成分分析的人脸识别. 2014, 44(3): 828-833
GU Bo-yu, SUN Jun-xi, LI Hong-zuo, LIU Hong-xi, LIU Guang-wen. Face recognition based on eigen weighted modular two-directional two-dimensional PCA. 吉林大学学报(工学版), 2014, 44(3): 828-833 复制到剪切板

Permissions

基于特征加权模块双方向二维主成分分析的人脸识别

顾播宇, 孙俊喜, 李洪祚, 刘红喜, 刘广文

长春理工大学电子信息工程学院,长春 130022

孙俊喜(1971),男,教授,博士生导师.研究方向:图像处理与模式识别.E-mail:junxi_sun@126.com

顾播宇(1984),男,博士研究生.研究方向:通信与信息系统.E-mail:guboyu1101@163.com

基金:国家自然科学基金项目(60977052); 吉林省科技发展计划项目(20100312);

摘要

对模块双方向二维主成分分析(Two-directional two-dimensional principal component analysis, (2D)2PCA)人脸识别算法进行了改进,提出了基于特征加权模块(2D)2PCA的人脸识别算法。首先对图像进行分块及(2D)2PCA特征提取。然后依据每一子图像块的特征对识别的贡献程度分配特征权重。最后对测试样本采用加权距离进行最近邻分类。该算法无需任何先验知识,依据子图像块在特征空间中的信息比重确定其贡献程度,从而实现自适应权重分配。试验结果表明:本文算法能够有效地提高人脸识别的正确率。

关键词: 信息处理技术; 模式识别; 人脸识别; 主成分分析; 特征加权; 特征提取

中图分类号:TN911.73 文献标志码:A 文章编号:1671-5497(2014)03-0828-06

Face recognition based on eigen weighted modular two-directional two-dimensional PCA

GU Bo-yu, SUN Jun-xi, LI Hong-zuo, LIU Hong-xi, LIU Guang-wen

School of Electronic and Information Engineering, Changchun University of Science and Technology, Changchun 130022, China

Fund:

Abstract

An improved modular Two-directional Two-dimensional Principle Component Analysis (2D(PCA)) with eigen weight for face recognition is proposed. First, the image is divided into sub-blocks and the features are extracted by modular 2D(PCA). Then, the feature weight is assigned to each sub-block of every image according to the contribution for recognition of the sub-block. Finally, the testing samples are classified by nearest neighborhood classification of weighted distance. The contribution of each sub-block is determined self-adaptively according to the proportion of local feature information in eigen space. This algorithm does not need any prior knowledge. Experimental results show that the recognition rate of the proposed algorithm is effectively improved.

Keyword: information processing; pattern recognition; face recognition; principal component analysis(PCA); eigen weighted; feature extraction

Show Figures

0 引言

目前,基于学习的统计识别已成为人脸识别的主流方法,然而统计识别面对的特征维数往往较高,导致算法的时间复杂度和空间复杂度都大大增加,而且高维特征空间的参数估计也变得困难,因此,人们常常需要对原始高维特征集合进行特征提取或特征变换以便获得有效的人脸识别特征^{[ 1, 2]}。作为最小均方误差意义上的数据最优特征变换方法——主成分分析(Principal component analysis,PCA)被广泛应用于人脸识别领域^{[ 3, 4, 5]}。但是,PCA对表情和姿态等条件变化缺乏稳健性,为此,Gottumukkal等^{[ 6]}提出模块PCA(Modular PCA)人脸识别算法,该算法将图像分为若干子图像块并分别进行PCA特征提取,获得了良好的效果。在特征提取过程中,PCA算法需要将图像矩阵转化成维数较高的图像向量,计算量庞大,为此,Yang等^{[ 7]}提出2DPCA(Two-dimensional PCA)方法,该方法直接利用图像矩阵,从而构造出维数较低的协方差矩阵,降低了计算强度并提高了稳健性,文献[8]将其拓展,提出了模块2DPCA,进一步提高了识别率。

随后,许多一维算法被扩展至二维,目前,二维方法已成为研究的热点。文献[9]指出,2DPCA可看作按行(或列)分块的模块PCA,而为了进一步降低图像维数并加快识别速度,Zhang等^{[ 10]}提出(2D)²PCA,该算法在行列两个方向上对图像进行2DPCA特征提取。在此基础上,针对单样本条件下的人脸识别问题,文献[11]于2010年提出将加权和分块与(2D)²PCA算法相结合的MW(2D)²PCA算法,该算法对各投影轴赋予不同权值,从而提高了稳健性。然而,在模块(2D)²PCA算法中,各子图像块对识别结果的贡献程度被认为是等价的。考虑到人类常常能够根据某一具有代表性的物理特征(如眼睛、鼻子、嘴等)来进一步辨识人脸^{[ 12]},对于同一人脸图像,其不同的局部特征对最终识别结果的贡献程度应不相同。PCA的本质是一种数据重组变换,而人脸图像中对识别贡献较大的物理空间特征,在变换过程中应以某种抽象形式在特征空间中得到体现。因此,通过贡献程度对不同子图像块分配不同权重应是提升稳健性的有效方法。

基于此,本文提出了基于特征加权模块(2D)²PCA的人脸识别算法,该算法首先对图像进行分块并提取模块(2D)²PCA特征,再根据人脸图像的各部分在特征空间中的信息比重进行特征加权,最后通过加权距离完成人脸分类。

1 模块(2D)²PCA人脸识别算法

1.1 训练过程

若训练样本数为p个,将每个样本分为m×n个子图像块,则样本空间中的某一样本可表示为:

(1)

样本空间 I中共含 p×m×n个图像矩阵,若图像分辨率为 M×N,则每个图像矩阵大小为 M/m×N/n。

样本空间均值可表示为:

μ = I _ijk (2)

样本空间中任意图像矩阵 I _l( l=ijk)及均值 μ可分别表示为由列向量或行向量所构成的形式:

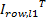
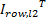
I _l ={ I_col, _l₁, I_col, _l₂,…, I_col, _lh} ={ , ,…, }^T;

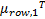
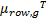
μ ={ μ_col,1, μ_col,2,…, μ_col, _h} ={ , ,…, }^T;

h=N/n; g=M/m。

通过样本均值对所有图像向量进行中心化,并分别按行列两个方向计算样本空间的协方差矩阵:

(3)

式中: Γ_col, _lt和 Γ_row, _lt分别为列方向和行方向上的中心化图像向量, Γ_col, _lt = I_col, _lt - μ_col, _t; Γ_row, _lt = I_row, _lt - μ_row, _t。

计算列方向协方差矩阵 C_col的全部特征值 λ_col =diag{ λ_col,1, λ_col,2,…, λ_col, _h},将特征值按降序排列,选取前 σ个( σ≤ h)大于零的特征值所对应的单位正交特征向量构成特征向量组 E_col ={ E_col,1, E_col,2,…, E_col, _σ}, θ确定如下:

(4)

式中: θ为预先设置的阈值,当θ≈0.9时效果最佳。

同样,选取 C_row的 δ( δ≤ g)个特征值,得到特征向量组 E_row ={ E_row,1, E_row,2,…, E_row, _δ}。每个特征向量即为特征空间中的一个投影轴。通过 E_col和 E_row,将第 i个样本的第 jk块向特征空间中投影:

η _ijk= ( I _ijk- μ) E_row(5)

1.2 分类过程

任意测试样本的第 jk个子图像块,可由一图像矩阵 I_test, _jk表示,将其由样本空间向特征空间投影:

η_test, _jk= ( I_test, _jk- μ) E_row(6)

在特征空间中,计算测试样本与第i个训练样本的距离:

d _i= 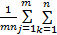‖ η_test, _jk- η _ijk‖ (7)

式中:‖·‖为Frobenius范数。

与测试样本距离最小的训练样本所属类别 ρ即为识别结果:

ρ= 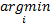d _i( I _i∈ I _ρ) (8)

2 特征加权模块(2 D)² PCA

2.1 特征加权

首先对样本空间中每一图像矩阵进行中心化:

Z _ijk= I _ijk- μ(9)

将每个中心化图像矩阵看作一个由 r维随机变量构成的列向量, r=M/m×N/n。所有中心化图像向量构成中心化样本集 Z,而每个随机变量可看作一个 p×m×n维行向量,因此 Z可看作所有 p×m×n个图像向量的集合,同时,也可将其看作所有 r个随机变量向量的集合:

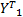
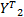
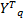
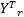
Z ={ Z₁₁₁, Z₁₁₂,…, Z₁ _mn,…, Z _ijk,…, Z _pmn}={ , ,…, ,…, }^T(10)

式中: Z _ijk为第 i个训练样本中第 jk个子图像块的中心化图像向量; Y _q为第 q个随机变量向量。

通过所有随机变量的统计信息计算训练样本集的协方差矩阵:

V = 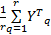Y _q (11)

计算 V的所有特征值 ε={ ε₁, ε₂,…, ε _pmn}及其对应的特征向量组 e={ e₁, e₂,…, e _pmn}。

特征值表示特征空间中,图像向量在其对应特征向量方向上的形变程度(即能量大小),通过特征值可计算训练样本集中第 l个图像向量在特征空间中的信息比重:

Λ _l = 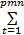ε _t( e _tl /v _ll)² l=1,2,…, pmn (12)

式中: e _tl为第 t个特征向量的第 l个元素; v _ll为协方差矩阵 V对角线上的相应元素。

在样本空间中,人类可根据人脸图像某一部分具有代表性的物理特征进行人脸辨识。而特征空间中,对于某一人脸图像不同子图像块的投影,其抽象特征同样体现出不同的信息比重,信息比重越大,则其对识别的贡献程度越高。

特征加权分配是将每一子图像块在整个图像中所占的信息比重量化为权重。在样本 i中,对 m×n个子图像块进行权重归一化处理,使其满足:

w _ijk =1(13)

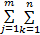
则第 i个训练样本中第 jk块的权重为

w _ijk =Λ _ijk / Λ _ilt(14)

2.2 加权距离

将训练样本和测试样本分别向模块2 DPCA特征空间投影,并计算测试样本与第 i个训练样本在第 jk个子图像块上的距离:

d _ijk =‖ η_test, _jk -η _ijk‖(15)

将测试样本与第 i个训练样本相应各子图像块的权重与距离相乘,得到加权距离矩阵:

(16)

将加权距离矩阵各元素相加,可得测试样本与该训练样本的加权距离:

Ω _i= 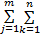ω _ijk (17)

通过最近邻分类进行识别,将测试样本归为与其加权距离最近的测试样本所属类别 ρ:

ρ= 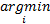Ω _i( I _i∈ I _ρ) (18)

3 试验结果及分析

试验采用 ORL人脸数据库对本文算法性能进行测试。图1为该库中来自某一对象的部分人脸图像。 ORL人脸库包含400幅分辨率为92 ×112的灰度图像,来自40个具有不同性别、种族、年龄的对象,对每人采集10幅不同表情和姿态的人脸图像,其人脸深度旋转和平面旋转达20 %,尺度变化达10 %。将该数据库分为40类,每类训练及测试样本总和为10幅。试验中未对图像进行任何预处理。

	Figure Option View Download New Window
	图1 ORL人脸库中部分图像Fig.1 Images from ORL database

3.1 本文算法与模块(2D)²PCA算法性能对比

图2为ORL人脸库中的一幅测试样本分别通过传统模块(2D)²PCA算法和本文算法的识别结果。试验中,将样本分为2×2个46×56大小的子图像块,并由式(9)~(13)计算各子图像块的特征权重,图2(c)为训练样本;(d)中参数为训练样本各子图像块所对应的权重系数。

	Figure Option View Download New Window
	图2 某一测试样本的识别结果对比Fig.2 Result comparison of a test sample

如图2所示,测试样本的姿态变化以及图2(b)和(c)中两个对象较为相近的外貌特征,共同导致传统模块(2D)²PCA识别错误。而本文算法通过细微调整各块的特征权重,强调了图像的局部差异,并降低形变造成的干扰,缩小测试样本与正确对象的距离,使其被正确分类。

在ORL人脸库中统计本文算法在选择不同投影轴数量(1~12个)时的识别率,并与传统模块(2D)²PCA进行对比,其结果如图3所示,坐标横轴上的ALL表示选取全部大于零的特征值对应的特征向量作为投影轴。试验中从每类中随机选择6幅图像构成训练样本集,其余用作测试,识别率为重复10次试验的平均结果。

图3中,两种算法的识别率均随投影轴数量的增加呈上升趋势,当投影轴增加至4个以后,识别率趋于稳定,在投影轴数量为6时识别率达到最高,此时,传统模块(2D)²PCA的识别率为96.06%,而本文算法可达96.82%,式(4)中的阈值 θ=0.904。

	Figure Option View Download New Window
	图3 两种算法的识别率对比Fig.3 Comparison of the two algorithms

试验结果表明,在投影轴数量达到4个后,本文算法始终有着更高的识别率(正确率提升了0.5%~0.94%),因此,与传统模块(2D)²PCA算法相比,本文算法表现出更强的稳健性。

由图3可知,当投影轴超过10个后,识别率出现小幅下降,这是由于图像中的某些冗余信息被引入特征空间。当投影轴数量小于4时,本文算法识别率低于传统模块(2D)²PCA算法,其原因为:在特征提取过程中,特征空间的维数过低会使许多重要的图像信息丢失,导致权重系数的置信度大幅降低。可见,选择适当数量的投影轴能够在完整的表示图像信息的同时降低冗余。

3.2 单样本条件下的性能对比

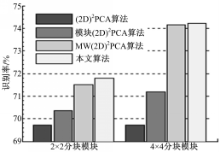
为了验证在模块(2D)²PCA中,基于特征空间中的信息比重对各子图像块进行特征加权的可靠性,以及本文算法针对单样本问题的有效性,在ORL人脸库中将本文算法与(2D)²PCA算法、模块(2D)²PCA算法及MW(2D)²PCA算法进行对比,其结果如图4所示。

	Figure Option View Download New Window
	图4 单样本条件下的识别率对比Fig.4 Comparison of single training sample

试验中,每类任取1幅图像用作训练,构成单样本问题,其余用作测试,识别率为10次试验的平均结果。在2×2分块模式下时,投影轴数量取6, θ=0.904;在4×4分块模式下时, θ=0.929,选择4个投影轴进行特征提取。

如图4所示,(2D)²PCA算法的识别率为69.72%。在2×2分块模式下,模块(2D)²PCA算法的识别率为70.36%,MW(2D)²PCA算法的识别率达71.5%,本文算法识别率相对略高,为71.78%。在4×4分块模式下,模块(2D)²PCA算法的识别率为71.19%,MW(2D)²PCA算法的识别率可达74.14%,本文算法为74.22%。可见,在单样本条件下,相对于(2D)²PCA和模块(2D)²PCA算法,本文算法识别率有明显提高,而本文算法与MW(2D)²PCA算法的识别率基本持平。虽然相对于MW(2D)²PCA算法,本文算法并没有显著地提升正确率,但其依然存在一个明显的优势:在MW(2D)²PCA算法中,最佳权值系数是通过多次试验得出的,而本文算法的权重分配过程则完全是自适应的。

3.3 算法速度分析

在许多人脸识别的实际应用中,算法的运行速度直接影响其实用性。表1为本文算法与模块(2D)²PCA算法在Matlab 7.6中的时间消耗对比,其测试环境为主频2.6 GHz的AMD双核PC机,时间消耗为10次测试的平均结果。

表1 时间消耗对比 Table 1 Comparison of time consumption

如表1所示,在训练过程中,本文算法由于引入特征加权的计算,导致时间消耗略有上升(约为9.3%)。而分类过程中,本文算法耗时与传统模块(2D)²PCA算法几乎一致。在实际应用中,训练过程并不对识别速率产生影响,因此本文算法在有效提升识别率的同时,其速度与传统模块(2D)²PCA算法保持一致,特征加权的引入并未造成识别速率和实用性的降低。

4 结束语

对模块(2D)²PCA算法进行扩展,提出了一种基于特征加权模块(2D)²PCA的人脸识别算法。在ORL人脸库上进行测试,结果表明:相对于传统模块(2D)²PCA算法,本文算法能够有效提高人脸识别的正确率,并且在单样本条件下同样表现出较强的稳健性。证实了基于各子图像块在特征空间中的信息比重进行自适应权重分配的可靠性。在特征权重分配的过程中,本文算法无需任何先验知识以及人为干预,以各子图像的抽象特征为依据,在特征空间中计算权重系数,从而实现自适应特征加权,并有效地强调对识别贡献程度较高的图像局部特征。本文通过加权描述图像局部所包含的特征信息量,通过(2D)²PCA进行人脸识别,文中所提出的局部特征加权方法同样可与其他算法,如kernel-PCA、ICA等算法相结合使用。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Jafri R, Arabnia H R. A survey of face recognition techniques[J]. Journal of Information Processing Systems, 2009, 5(2): 41-68. [本文引用:1]
[2]	Tan X, Chen S, Zhou Z H, et al. Face recognition from a single image per person: A survey[J]. Pattern Recognition, 2006, 39(9): 1725-1745. [本文引用:1] [JCR: 2.632]
[3]	Kirby M, Sirovich L. Application of the KL procedure for the characterization of human faces[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(1): 103-108. [本文引用:1] [JCR: 4.795]
[4]	Turk M A, Pentland A P. Face recognition using eigenfaces[C]∥1991 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1991: 586-591. [本文引用:1]
[5]	宋怀波, 史建强. 应用PCA理论进行多人脸姿态估计的方法[J]. 吉林大学学报: 工学版, 2013, 43(增刊1): 43-46. Song Huai-bo, Shi Jian-qiang. Pose estimation of varied human faces based on PCA method[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(Sup. 1): 43-46. [本文引用:1] [CJCR: 0.701]
[6]	Gottumukkal R, Asari V K. An improved face recognition technique based on modular PCA approach[J]. Pattern Recognition Letters, 2004, 25(4): 429-436. [本文引用:1] [JCR: 1.266]
[7]	Yang J, Zhang D, Frangi A F, et al. Two-dimensional PCA: a new approach to appearance-based face representation and recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(1): 131-137. [本文引用:1] [JCR: 4.795]
[8]	陈伏兵, 陈秀宏, 张生亮, 等. 基于模块 2DPCA 的人脸识别方法[J]. 中国图象图形学报, 2006, 11(4): 580-585. Chen Fu-bing, Chen Xiu-hong, Zhang Sheng-liang, et al. A human face recognition method based on modular 2DPCA[J]. Journal of Image and Graphics, 2006, 11(4): 580-585. [本文引用:1] [CJCR: 0.758]
[9]	Gao Q. Is two-dimensional PCA equivalent to a special case of modular PCA?[J]. Pattern Recognition Letters, 2007, 28(10): 1250-1251. [本文引用:1] [JCR: 1.266]
[10]	Zhang D, Zhou Z H. ( 2D)2PCA: Two-directional two-dimensional PCA for efficient face representation and recognition[J]. Nerocomputing, 2005, 69(1): 224-231. [本文引用:1]
[11]	李欣, 王科俊, 贲晛烨. 基于MW(2D)2PCA的单训练样本人脸识别[J]. 模式识别与人工智能, 2010(1): 77-83. Li Xin, Wang Ke-jun, Ben Xian-ye. MW(2D)2PCA Based face recognition with single training sample[J]. Pattern Recognition and Artificial Intelligence, 2010(1): 77-83. [本文引用:1] [CJCR: 0.7855]
[12]	张翠平, 苏光大. 人脸识别技术综述[J]. 中国图象图形学报, 2000, 5(11): 885-894. Zhang Cui-ping, Su Guang-da. Human face recognition: a survey[J]. Journal of Image and Graphics, 2000, 5(11): 885-894. [本文引用:1] [CJCR: 0.758]

2009

0.0

... 0 引言目前,基于学习的统计识别已成为人脸识别的主流方法,然而统计识别面对的特征维数往往较高,导致算法的时间复杂度和空间复杂度都大大增加,而且高维特征空间的参数估计也变得困难,因此,人们常常需要对原始高维特征集合进行特征提取或特征变换以便获得有效的人脸识别特征^[1,2] ...

2006

2.632

0.0

1990

4.795

0.0

... 主成分分析(Principal component analysis,PCA)被广泛应用于人脸识别领域^[3,4,5] ...

1991

0.0

... 主成分分析(Principal component analysis,PCA)被广泛应用于人脸识别领域^[3,4,5] ...

2013

0.0

0.701

. 2013, 43(增刊1):43-46

Pose estimation of varied human faces based on PCA method

1. College of Mechanical and Electric Engineering, Northwest A&F University, Yangling 712100, China;<br />2. School of Mechanical Engineering, Xi'an Jiaotong University, Xi'an 710049, China

Pose estimation of different human faces is a key technology of varied human face recognitions which has not been well resolved yet.In order to get the mapping between face poses and feature spaces,an algorithm based on PCA was presented to realize the face pose estimations.Firstly,the subspaces and eigenvectors of different poses was built and selected by using PCA theory.Secondly,the Euclidean distance classifier was chosen to estimate the multi-poses of human faces.Lastly,the relationship between PCA's Variance contribution rates and pose estimation accuracy rates was investigated in detail.The algorithm was validated by means of experimental tests of human face pose database,which contains 23 kinds of poses and 630 samples in detail;experimental results show that the precision of this algorithm is above 84%.It also shows that the PCA based pose estimation method is feasible and valid for varied human face recognition.

多人脸姿态估计是多姿态人脸识别的关键问题,至今尚未很好地解决。本文提出了一种基于PCA(Principal Component Analysis)算法的多人脸姿态估计方法,以获得人脸姿态与人脸图像在特征空间投影间的对应关系。算法首先利用PCA理论构建训练样本集的姿态子空间与特征向量,然后利用欧氏投影距离进行姿态估计,最后对方差贡献率与姿态估计准确率间的关系进行了研究。为了验证算法的有效性,利用23类姿态,共690个样本进行了实验,实验结果表明,该方法的姿态估计准确率为84%。说明将该方法应用与多姿态人脸估计是有效的,可行的。

... 主成分分析(Principal component analysis,PCA)被广泛应用于人脸识别领域^[3,4,5] ...

2004

1.266

0.0

. 2004, 25(4):429-436 DOI:10.1016/j.patrec.2003.11.005

An improved face recognition technique based on modular PCA approach

Abstract

A face recognition algorithm based on modular PCA approach is presented in this paper. The proposed algorithm when compared with conventional PCA algorithm has an improved recognition rate for face images with large variations in lighting direction and facial expression. In the proposed technique, the face images are divided into smaller sub-images and the PCA approach is applied to each of these sub-images. Since some of the local facial features of an individual do not vary even when the pose, lighting direction and facial expression vary, we expect the proposed method to be able to cope with these variations. The accuracy of the conventional PCA method and modular PCA method are evaluated under the conditions of varying expression, illumination and pose using standard face databases.

... 但是,PCA对表情和姿态等条件变化缺乏稳健性,为此,Gottumukkal等^[6]提出模块PCA(Modular PCA)人脸识别算法,该算法将图像分为若干子图像块并分别进行PCA特征提取,获得了良好的效果 ...

2004

4.795

0.0

... 在特征提取过程中,PCA算法需要将图像矩阵转化成维数较高的图像向量,计算量庞大,为此,Yang等^[7]提出2DPCA(Two-dimensional PCA)方法,该方法直接利用图像矩阵,从而构造出维数较低的协方差矩阵,降低了计算强度并提高了稳健性,文献[8]将其拓展,提出了模块2DPCA,进一步提高了识别率 ...

2006

0.0

0.758

2007

1.266

0.0

. 2007, 28(10):1250-1251 DOI:10.1016/j.patrec.2007.02.005

Is two-dimensional PCA equivalent to a special case of modular PCA

Abstract

In this note, we point out that 2D-PCA is not a special case of MPCA. 2D-PCA views the rows of images as training samples that constitute m sub-training sets instead of original images, where m is equivalent to the row of images. It then uses these sub-training sets to evaluate the covariance matrix for images. Finally, the main difference between these two methods is shown.

2005

0.0

... 文献[9]指出,2DPCA可看作按行(或列)分块的模块PCA,而为了进一步降低图像维数并加快识别速度,Zhang等^[10]提出(2D)²PCA,该算法在行列两个方向上对图像进行2DPCA特征提取 ...

2010

0.0

0.7855

. 2010, 2010(1):77-83

MW(2D)2PCA Based face recognition with single training sample

传统的人脸识别方法在单训练样本条件下性能会急剧下降,因此,研究出适合于单样本情况下的识别算法是人脸识别问题面临的巨大挑战.针对两个方向的二维主成分分析((2D)~2PCA)算法进行改进,文中提出将加权和分块与(2D)~2PCA相结合的方法称为分块加权(2D)~2PCA,以便更有效地提取人脸的局部特征.同时把模糊理论引入分类决策,应用于单训练样本人脸识别问题.在ORL人脸库以及部分CAS-PEAL人脸库中的实验结果表明,文中方法能取得较好的识别效果.

Abstract：

Traditional methods get low recognition accuracy in the condition of only one training sample,therefore,it is a great challenge for face recognition.In this paper,a two-directional two-dimensional principal component analysis((2D)~2PCA)is developed to solve this problem.An improved arithmetic combining weight and block called modular weighted(2D)~2PCA is proposed for efficient local feature extraction.Besides,the fuzzy theory is introduced to classify the single sample face recognition.Experimental results on ORL and a subset of CAS-PEAL face databases show that the presented method achieves a high recognition accuracy.

2000

0.0

0.758

... 考虑到人类常常能够根据某一具有代表性的物理特征(如眼睛、鼻子、嘴等)来进一步辨识人脸^[12],对于同一人脸图像,其不同的局部特征对最终识别结果的贡献程度应不相同 ...