张金果(1971),男,副教授.研究方向:计算机应用,控制理论与控制工程.E-mail:505227895@qq.com
利用一维属性直方图改进交叉Tsallis熵,在此基础上提出了一种基于一维属性直方图的对称最小交叉Tsallis熵水下小目标声呐图像分割方法。该方法的主要步骤是:①抑制水下小目标声呐图像的散斑噪声;②根据图像像素的灰度值和该像素邻域的灰度平均值的大小建立属性集,在属性集上建立与该属性集约束对应的一维属性直方图;③根据一维属性直方图的对称交叉最小Tsallis熵法确定灰度二值化阈值;④对二值化后的图像去除孤立区。实验结果表明:该方法适用于直方图为复杂非双峰形状的水下小目标声呐图像,而且与现有的属性直方图上的一维最大熵阈值化法比较,具有更强的抗噪能力。
A segmentation method on the sonar image of a small underwater target is proposed. In this method, the gray-level threshold for segmentation is acquired via the minimum symmetric Tsallis cross entropy that is based on one-dimensional bound histogram. In this method, first, the speckle noise of the sonar image is suppressed. Second, the bound set is constructed according to the restriction in the gray-level values of both pixels and their neighborhood averages, and the one-dimensional bound histogram corresponding to that bound set is established. Third, the gray-level threshold for segmentation is determined according to the minimum symmetric Tsallis cross entropy based on the one-dimensional bound histogram. Finally, the isolated areas in the threshold image are removed. Experimental results show that the proposed method is well adequate for the images with a nonideal bimodal histogram; it has better antinoise performance than the existing methods based on the entropy of the one-dimensional bound histogram.
在众多的图像分割方法中,阈值法是一类最重要最基本的图像分割方法。在阈值法中,基于熵的阈值法占有重要的地位。较常用的基于熵的阈值法主要有Pun[ 1]提出的最大后验熵上限法、Kapur[ 2]提出的一维最大熵法、Abutaleb[ 3]提出的二维熵阈值法、Li[ 4]提出的最小交叉熵方法、Brink[ 5]提出的对称交叉熵方法、Pal[ 6]提出的最小交叉熵方法等。这些基于熵的阈值法均采用Shannon熵,Shannon熵满足可加性(即广延性)[ 7]。Shannon熵的可加性没有考虑两个子系统间的相互作用。这样,基于Shannon熵的阈值法得到的阈值有时是不正确的[ 7]。而Tsallis熵具有非可加性,它考虑了两个子系统之间的相互作用,具有普适性且更为有效[ 7, 8]。文献[ 9]提出基于一维Tsallis熵的阈值法,文献[ 10]将这种方法推广到二维情况。文献[ 7, 8]在文献[ 9, 10]的基础上提出了两种最小交叉Tsallis熵阈值法。这些方法对于某些图像阈值化问题效果较好,但如果图像的一维灰度直方图呈复杂的非理想双峰形状,用这些方法通常无法得到正确的分割阈值。
属性直方图[ 11]概念是直方图概念的推广,作为一种受约束的直方图,属性直方图可以使问题简化。文献[ 12]根据二维属性直方图的最大熵法分割声呐图像。并根据声呐图像像素的灰度值和该像素邻域的灰度平均值的大小建立属性集,该方法具有较强的抗干扰能力,但计算耗时长。文献[ 13]利用一维属性直方图的最大熵进行海底小目标声呐图像分割,它利用文献[ 12]中的思路建立属性集,但它与文献[ 12]中的方法又不完全相同,它是基于一维属性直方图的。实验证明文献[ 13]提出的方法具有较强的抗干扰能力和较小的计算量。基于属性直方图的这些阈值化方法适用于其直方图不是理想的双峰形状的图像,鉴于此,本文利用一维属性直方图改进交叉Tsallis熵,得到一种基于一维属性直方图的最小交叉Tsallis熵水下小目标声呐图像分割方法。由于利用交叉Tsallis熵,本文方法与文献[ 13]方法不同。另外,散斑噪声严重影响水下小目标声呐图像的分割,因此本文的分割方法中含有散斑噪声抑制环节。而文献[13]的方法中不含有散斑噪声抑制环节。
作者曾将直方图的概念推广,提出属性直方图的概念[ 11, 13]。一维属性直方图的概念简述如下。
将图像的全体像素视为论域X={(i,j)├|:┤0≤i<M,0≤j<N},其中M为图像的宽度,N为图像的高度。Q为论域(或图像)X上的一个属性集, 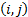

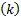
pQ = = 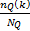 | (1) |
式中:nQ 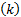
由于它只考察图像中遵循约束Q或具备属性Q的像素,一维属性直方图是一种残缺的直方图。这种残缺性使一维属性直方图具有这样的特性:不考虑通常直方图中遵循一定约束的干扰或具体实际问题中不关心的子图或像素。这样就可以使待处理的问题简化。根据一维属性直方图解决具体实际问题时首要的问题是创建一维属性直方图,而这一问题的核心与基础是建立属性集Q。
设P1=(p11,p12,…,p1N)和P2=(p21,p22,…,p2N)表示任意两个概率分布,满足p1i≥0,p2i≥0, 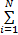
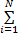
D(P1∶P2)= p1i p1i 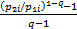 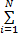 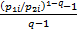 | (2) |
式中:q>0为某一常数。
Tsallis熵考虑了两个概率分布之间Tsallis熵意义下的信息量差异,当两个分布完全相同时,其取最小值。
假定用t作为阈值将图像X分割为目标Co={(i,j)|X(i,j)=0,1,…,t}和背景Cb={ (i,j)|X(i,j)=t+1,t+2,…,L-1}。基于属性集与属性直方图的目标先验概率PQo、背景先验概率PQb如下:
PQo=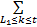 pQ pQ  | (3) |
PQb= pQ pQ  | (4) |
由式(3)(4)得到基于属性集和属性直方图的目标灰度均值μQo、背景灰度均值μQb如下:
μQo=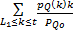 | (5) |
μQb=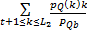 | (6) |
式中:L1、L2分别为属性集中像素灰度的最小值和最大值。
由式(1)得基于属性集和属性直方图的总体均值为:
μ= 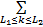

令
pi,j=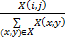 | (8) |
qi,j=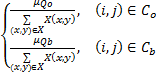 | (9) |
由式(8)(9)知:pij,qij≥0; 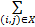
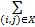
D(P1∶P2)=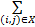 pi,j pi,j  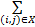 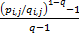 | (10) |
由式(5)~(10)得:
D(P1∶P2)= 

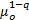
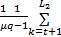
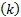
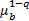
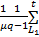


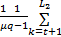
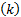
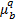
D(P1∶P2)反映了分割前后图像之间的差异,当其取最小值时,目标和背景内部灰度均匀,分割效果最佳。分割阈值t为:
t=argmin[D(P1∶P2)] (12)
声呐系统的换能器向水底探测区域发射超声波,经过水底和水底目标区的反射,换能器接收回波,经过多波束形成等处理后采样各波束数据,构成一幅距离方位的二维水下小目标声呐图像。图1是一个柱形目标不同成像条件下的两幅二维声呐图像。图1中较大的亮区与回波较强的区域相对应,是小目标本身回波形成的,称为目标亮区;与目标亮区相邻的其后面的暗区与水下小目标声学阴影相对应,称为目标暗区。目标暗区的形状与水下小目标的形状有关。图1中其余大部分是面积更小的或亮或暗区域,其平均灰度介于目标亮区与目标暗区的平均灰度之间,该部分是海(或河、湖)底混响形成的,称为海(或河、湖)底混响区。与通常的可见光学图像相比,水下小目标声呐图像总体来看对比度低,分辨率低,干扰强,目标暗区像素少,边缘恶化。
水下小目标声呐图像中含有严重的散斑噪声影响了分割的准确性,因此分割前首先抑制水下小目标声呐图像的散斑噪声。由于阈值化后的图像中通常含有多个独立的干扰区域,因此阈值化后还需去除图像孤立区。
3.2.1 散斑噪声抑制
先将图1所示的两幅图像(a)(b)实施同态变换,再实施模糊加权均值滤波[ 14];然后实施指数变换,得到抑制散斑噪声后的水下小目标声呐图像,分别见图2(a)(b)。
3.2.2 构造属性集Q和建立一维属性直方图
水下小目标声呐图像分割目的是分离出目标暗区。考虑水下小目标声呐图像的灰度值和噪声特点,结合其分割的目的,这样构造属性集Q:
Q=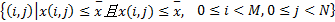 | (13) |
式中:x(i,j)、x(i,j)分别为像素(i,j)的灰度值、像素(i,j)邻域内灰度的平均值; 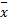
由于水下小目标声呐图像中目标亮区、水底混响区、目标暗区的灰度均值呈现由大到小的变化规律,所以在排除噪声的情况下,水下小目标声呐图像中的目标暗区的像素灰度值与邻域均值应该小于整幅声呐图像的灰度均值,而目标亮区和部分水底混响区的像素灰度值将大于整幅声呐图像的灰度均值,所以由式(13)建立的属性集Q由目标暗区和部分水底混响区组成,即这样建立的属性集Q已经排除了目标亮区和部分水底混响区。
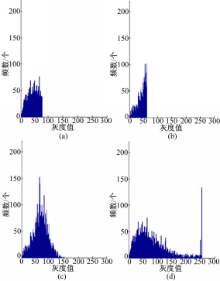
由式(1)和(13)建立如图3(a)和(b)所示的属性集Q上的一维属性直方图。图中横坐标表示灰度值,纵坐标表示频数(下文同)。作为比较,也给出通常意义下的一维直方图,分别见图3(c)与(d)。通过比较易见,一维属性直方图中的干扰较少,而通常意义下的一维直方图中存在过多的干扰成分,不是理想的双峰形状。
3.2.3 阈值化
利用式(12)计算图2(a)和2(b)所示图像的分割阈值分别为44,51。利用这两个分割阈值二值化图2(a)和2(b)的图像,其结果对应于图4(a)(b)。作为比较,也给出文献[13]方法二值化后的图像,分别见图5(a)(b)。可见,图4(a)的干扰较图5(a)小,图4(b)的干扰较图5(b)小,即本文方法较文献[13]方法的抗干扰能力更强。
如果不利用一维属性直方图,而是利用通常意义下的一维直方图,应用对称交叉最小Tsallis熵阈值化方法对水下小目标声呐图像进行阈值化,则无法得到正确的结果,因为通常意义下的一维直方图中存在过多的干扰成分,不是理想的双峰形状。
另外,由于本文方法采用一维属性直方图,其计算量也小于直接利用通常意义下的一维直方图的对称交叉最小Tsallis熵阈值化方法,其计算量大约为后者的(L2-L1)/L倍(这里L为图像的灰度级)。
3.2.4 去孤立区
图4(a)(b)所示图像中含有若干个称之为孤立区的小的黑色区域。这些孤立区面积一般远小于目标暗区面积。根据这个特点,可以借助于区域标记法将各个孤立区去掉而保留目标暗区,去除孤立区后的图像如图6所示。图6(a)(b)分别与图4(a)(b)对应。
本文利用一维属性直方图对对称交叉最小Tsallis熵阈值化方法进行改进,拓展了对称交叉最小Tsallis熵阈值化方法的适用范围,改进后的方法适用于直方图为复杂非双峰形状的水下小目标声呐图像。
与作者在文献[13]中提出的基于一维属性直方图的水下小目标声呐图像二值化方法相比,本文方法抗干扰能力更强,计算量处于同一量级。另外,本文的分割方法中含有抑制散斑噪声的环节,也使本文方法的适用性更强。
本文方法适用于有一定约束或先验知识的水下小目标声呐图像的分割,也适用于有一定约束或先验知识的其他图像的分割。如果图像本身无约束或先验知识,这里提出的方法将退化变成为一般意义下的对称交叉最小Tsallis熵阈值化方法。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|