富爽(1982),女,博士研究生.研究方向:认知无线电.E-mail:fushuang_dq@163.com
根据信号和噪声频域Sevcik分形维数特征的不同,计算接收信号的频域Sevcik分形维数,通过与预先设定的门限值进行比较,判断主用户的存在与否。该方法具有对噪声不确定性不敏感、不需要主用户信号先验知识以及在低信噪比时能够达到较高的检测概率的优点,且运算时间短,可用于噪声具有不确定性、低信噪比情况下的快速盲频谱感知。Monte Carlo仿真结果表明:在噪声不确定度为±5 dB的情况下,当信噪比大于-12 dB时,该方法对于7种不同调制类型的信号的平均检测概率能够达到100%。
A fast blind spectrum sensing method using Sevcik fractal dimension in frequency domain is proposed. First, the Sevcik fractal dimension in frequency domain of the received signal is calculated. Then according to the difference of Sevcik fractal dimension characters between signal and noise, the calculation result is compared with the predefined threshold to determine whether the primary user exists. Compared with existing spectrum sensing methods, the proposed method has some advantages, such as insensitive to noise uncertainty, not requiring priori knowledge, and high detection probability in low SNR situation. Furthermore, it consumes less calculation time. This method can be applied to fast blind spectrum sensing in the situation of low SNR and noise uncertainty. Monte Carlo simulation results show that its average detection probability of signals with 7 modulation types can reach 100% when SNR is larger than -12 dB with ±5 dB noise uncertainty.
认知无线电技术[ 1]的出现为目前频谱资源日益紧张的问题提供了一种有效的解决方案,是未来无线通信发展的必然趋势。其实现的关键和前提是准确、有效的频谱感知技术[ 2, 3, 4]。目前的单节点频谱感知技术主要有匹配滤波检测、循环平稳特征检测和能量检测[ 5, 6, 7]。匹配滤波检测能够达到较好的检测效果,但需要主用户信号的先验知识。循环特征检测利用信号的循环平稳性进行频谱感知,但该方法计算复杂,运算量大。能量检测是目前广泛采用的方法,但该方法在低信噪比下检测性能较差,另外由于信噪比墙[ 8]的存在,在噪声具有不确定性的情况下,其检测性能会急剧下降。而认知无线电技术要求检测器必须能够检测非常微弱的主用户信号,因此寻找快速、准确的频谱感知技术是目前认知无线电发展亟待解决的问题。
分形维数是信号复杂度和随机性的一种度量手段。Kordan提出使用Higuchi分形维数进行盲频谱感知的方法[ 9],但该方法在低信噪比下的准确度较低。赵春晖提出了基于分形盒维数的频谱感知方法[ 10]。陈小波提出了基于分形盒维数的双门限合作频谱感知方法[ 11]和基于双门限的盒维数与信息维数的协作感知方法[ 12]。但以上利用时域盒维数进行频谱感知的方法存在一定的局限性,如对于一些调制类型中某些调制参数的信号无法检测,此外在低信噪比下检测效果较差。Zhang利用频域熵进行频谱感知,取得了较好的检测效果[ 13]。Sevcik提出了一种计算波形分形维数的方法[ 14],即Sevcik分形维数,该方法能够快速估算波形的Hausdorff维数,度量波形的复杂性和随机性。
本文根据信号和噪声的频域Sevcik分形维数特征的不同,区分信号和噪声,进行快速盲频谱感知。该方法不需要主用户的先验知识,运算简单,在低信噪比下具有较高的检测性能,且对噪声不确定不敏感,可以用于噪声具有不确定性、低信噪比环境下的快速盲频谱感知。
Sevcik分形维数源于Hausdorff维数的计算方法,具体如下[ 14]:
设波形信号由一系列点(xi,yi)组成,长度为N,即0≤i≤N-1。首先对信号进行归一化,归一化后的一系列点( 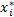
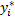
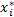 = = 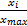 | (1) |
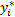 = = 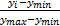 | (2) |
式中:x max为xi的最大值;y max、y min分别为yi的最大值和最小值。
则Sevcik分形维数D可由式(3)得出:
D=1+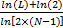 | (3) |
式中:L为波形的长度,其表达式为:
L=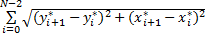 | (4) |
对于通信信号序列而言,x=0,1,2,…,N-1;x max=N-1; 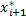
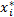
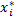 = = 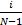 | (5) |
L=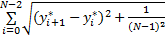 | (6) |
假设噪声ω(n)为独立同分布的加性高斯白噪声,其均值为0,方差为σ02;s(n)为主用户的发射信号,s(n)和ω(n)相互独立。则单节点的频谱感知可以抽象为一个二元假设检验模型:
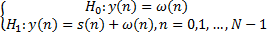 | (7) |
式中:y(n)为认知节点接收信号;H0代表主用户不存在;H1代表主用户存在。
s(n)可以是确定性信号(高斯白噪声信道),也可以是随机信号(衰落和多径效应信道)[ 15]。若为随机信号,假设s(n)服从均值为μ,方差为 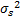
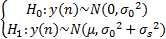 | (8) |
分形维数是一种度量信号复杂度和随机性的有效手段。在认知无线电频谱感知技术中,由于主用户信号为通信信号,其时域和频域的随机性和复杂度低于噪声,因此可以利用Sevcik分形维数度量接收信号的随机性,来判断主用户信号的有无。
本文以AM信号为例,研究信号的时域和频域Sevcik分形维数的特性。设信号s AM(t)= 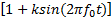
利用频域Sevcik分形维数进行频谱感知的方法的系统框图如图2所示。
具体计算方法如下:
对式(7)进行N点离散傅里叶(DFT)变换,得:
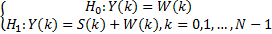 | (9) |
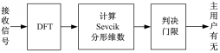 | 图2 利用频域Sevcik分形维数进行频谱感知方法的系统框图Fig.2 System chart of the fast blind spectrum sensing using Sevcik fractal dimension in frequency domain |
式中:Y(k)、W(k)和S(k)分别为y(n)、ω(n)和s(n)的离散傅里叶变换。
设 Y( k)、 W( k)和 S( k)分别为 Y( k)、 W( k)和 S( k)的模,利用式(2)对 Y( k)进行归一化,由于 Y( k)为 y( n)的 DFT,因此 Ymin可设为0,得:
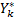 = = 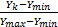 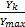 | (10) |
利用式(3)和式(6)计算 Y *( k)的 Sevcik分形维数 D,并将 D与预先设定的门限 λ比较,以判断主用户的存在与否:
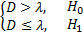 | (11) |
在假设H0时,即主用户不存在时, y( n) ~N(0, σ02)。对 y( n)进行 N点 DFT,得:
Y( k)= 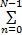

由于高斯分布的线性组合仍然是线性分布,故 Y( k)也服从高斯分布,计算其均值与方差为:
E[ Y( k)]= 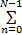
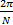
D[ Y( k)]=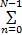 | (14) |
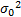
由于 Y( k)为复数, Y( k) =Yr( k) +jYi( k),因此实部 Yr( k)和虚部 Yi( k)分别满足高斯分布[ 15]:
Yr( k) ~N(0, 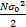
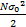
由 Y( k)= 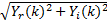
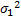
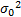
f Y( Y)= 
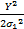
F Y( Y)= 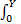
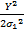
可得 Y( k)的均值 E[ Y]和方差 D[ Y]分别为:
E[ Y]=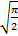 = = 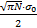 | (18) |
D[ Y]=(2- ) ) 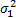  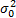 | (19) |
利用式(10)对 Y( k)进行归一化得 Y *( k) =Y( k) /Ymax,其中 Ymax可视为一个常数。 Y *( k)的期望和方差分别为:
E[ Y *] =E[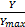 ]= ]= 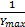 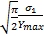 | (20) |
D[ Y *] =D[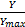 ]= ]= 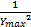  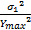 | (21) |
则式(6)中的 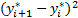
E[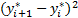 ]=2 E[ ]=2 E[ 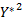 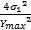 | (22) |
在以上分析中,一直将 Ymax看作是一个常数,但对于特定分布, Ymax为一个与 σ1有关的量。由概率论理论可得, Ymax的数学期望 E[ Ymax]为:
E[ Ymax] =NCσ1(23)
式中: C为一常数, C= 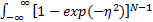
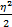
这样由式(3)(6)(22)(23)可得假设H0时 Sevcik分形维数的期望值为:
E[ D]=1+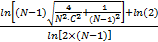 | (24) |
由式(24)可见,高斯白噪声的频域 Sevcik分形维数的数学期望与噪声功率 σ02无关,为一个常数,因此对噪声不确定性不敏感。
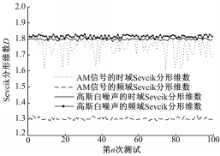
设序列长度N=5000。使用 Matlab对高斯白噪声在不同噪声功率下的频域 Sevcik分形维数进行仿真和计算,结果如图3所示。由图3可以看出:当噪声功率在-30 ~20 dBm内变化时,高斯白噪声的频域 Sevcik分形维数在均值1.814附近随机浮动,与噪声功率无关,因此不受噪声不确定性的影响,与式(24)所得结果一致。
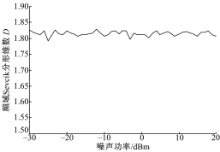 | 图3 噪声强度对高斯白噪声频域Sevcik分形维数的影响Fig.3 Effect of the noise intensity on Sevcik fractal dimension in frequency domain of white Gaussian noise |
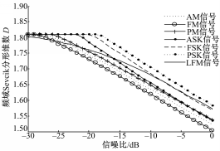
下面以载波频率为100 MHz的AM、FM、PM、ASK、FSK、PSK信号以及单位脉冲带宽为30 MHz的LFM信号为例,分析在不同噪声强度时信号的频域Sevcik分形维数特性。采样频率设为1 000 MHz。图4为7种不同调制类型信号在不同信噪比下的频域Sevcik分形维数。由图4可以看出:7种信号的频域Sevcik分形维数随着信噪比的增加而呈下降趋势。这是由于随着信噪比的增加,信号的随机性和复杂性也随之降低,因此,其分形维数也随之减少。将图3与图4比较可知,即使在主用户调制类型未知时的盲感知情况下,只要选取合适的门限,当信噪比大于一定值时,便可以将信号与噪声区分出来,以此判别主用户的存在与否。
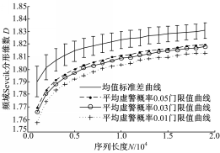
由式(24)可知,高斯白噪声的频域Sevcik分形维数只与序列长度N有关。因此,只要N确定,分形维数的期望便可确定,再根据虚警概率要求,式(11)中的门限值λ即可确定。门限值越高,主用户信号的检测概率和虚警概率越高,反之亦然,具体应根据对检测概率和虚警概率的要求而设定。图5为当N在1000~19 000之间变化时,其频域Sevcik分形维数的均值标准差曲线以及门限值曲线。所有结果均为10 000次计算后得到的平均值。其中,平均虚警概率0.05门限值曲线即第5百分位数曲线,由该曲线确定的门限值能够保证在该值以下的概率小于0.05,即平均虚警概率小于0.05,以此类推。由图5可以看出:随着N的增加,分形维数值也随之增加,且变化比较平稳。因此,只要序列长度N和虚警概率确定,门限值λ便随之确定。
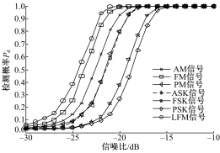
本文以AM、FM、PM、ASK、FSK、PSK和LFM七种不同调制类型信号为例,使用Monte Carlo方法对本文提出的利用频域Sevcik分形维数进行频谱感知的方法进行分析,Monte Carlo仿真次数为10 000次,每次仿真中各类型调制信号参数均在一定范围内随机变化。采样频率为1000 MHz。图6给出了7种不同调制类型信号在不同信噪比下的检测概率 Pd变化曲线。设平均虚警概率等于0.03,由图5可得门限值 λ=1.797。设 N=5000。由图6可以看出,当信噪比大于-15 dB时,7种信号均能够获得100%的检测概率,在低信噪比情况下能够达到较高的检测性能。
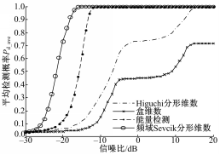
本文以AM、FM、PM、ASK、FSK、PSK和LFM七种调制类型信号的平均检测概率 Pd_ave为指标,对本文提出的利用频域Sevcik分形维数进行频谱感知的方法与文献[9]中的基于Higuchi分形维数进行盲频谱感知的方法、文献[ 10]提出的基于盒维数的频谱感知技术和能量检测方法进行比较。设 N=5000, λ=1.797,使平均虚警概率等于0.03。结果如图7所示。由图7可以看出:在同等情况下,本文方法明显优于能量检测、Higuchi分形维数法和盒维数法,在低信噪比下能够达到更高的检测性能。
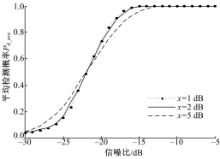
噪声不确定性广泛存在于实际的通信系统中,对噪声不确定性不敏感是检测器的基本要求。目前被广泛使用的能量检测方法,由于信噪比墙的存在,在噪声具有不确定性时检测性能严重下降。当存在x dB的噪声不确定性时,对于信噪比低于信噪比墙SNR wall=10 log10 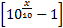
使用Matlab软件对本文方法、Higuchi分形维数法[ 9]、盒维数法[ 10]、能量检测以及循环平稳特征检测的运算时间进行比较。以本文方法 N=1000时进行1000次运算的时间为标准,对各算法时间进行归一化,结果如表1所示。由表1可以看出:本文方法的运算时间明显小于Higuchi分形维数法、盒维数法和循环平稳特征检测。在序列长度 N=1000时,其运算时间约为Higuchi分形维数法的1/5、盒维数法的1/8、循环平稳特征检测的1/800。频谱感知时间的减少,对减少感知开销、提高网络吞吐量都具有重要意义。相比以简单著称的能量检测方法,本文方法的运算时间虽然高于能量检测, 却能克服能量检测对噪声不确定性敏感和低信噪比下检测性能差的问题。
| 表1 归一化运算时间比较 Table 1 Comparison of the normalized computation time |
根据信号和噪声频域Sevcik分形维数特性的不同,提出了一种利用频域Sevcik分形维数进行快速盲频谱感知的方法。理论分析和仿真结果表明:高斯白噪声的频域Sevcik分形维数与噪声功率无关,因此利用频域Sevcik分形维数进行频谱感知的方法对噪声不确定性不敏感。该方法不需要主用户的先验知识,对噪声不确定性不敏感,运算速度快,在低信噪比下能具有较高的检测性能,可以用于噪声具有不确定性、低信噪比环境下的快速盲频谱感知。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|