高敬鹏(1980),男,博士研究生,讲师.研究方向:同步,信道估计与信号检测.E-mail:gjpmcu@126.com
针对最大似然检测算法复杂度高,最小二乘信道估计性能较差等缺陷,提出了一种SAGE-IGQS联合估计检测算法,该算法使用LS算法进行信道初始化,采用SAGE算法进行信道迭代估计,并结合改进的Grover量子搜索算法进行信号检测,从而提高了系统的有效性。理论研究和仿真结果表明:该算法在降低系统复杂度的情况下,误比特率性能优于传统的联合检测算法,与理想信道估计下的最大似然检测算法相接近。
To overcome the disadvantages of high computational complexity of maximum likelihood detection algorithm and the poor performance of the Least Square (LS) channel estimation, a new joint estimation and detection algorithm is proposed. In order to improve the system effectiveness, LS algorithm is applied to initialize channel and Space-alternating Generalized Expectation-maximization (SAGE) algorithm is employed to process channel iterative estimation. The proposed algorithm combines the improved Grover quantum search algorithm in signal detection. Theoretical study and simulation results show that bit error rate performance of proposed algorithm is better than that of traditional joint detection algorithm. Ideal channel estimation under the maximum likelihood algorithm can be approached by the proposed algorithm with low complexity.
MIMO(Multiple input multiple output)技术充分利用空间资源,实现多个天线并发并收,在不增加频谱资源和天线发送功率的情况下,可以成倍地提高信道容量。OFDM(Orthogonal frequency division multiplexing)技术是多载波窄带传输的一种,其子载波之间相互正交,使其高效利用频谱资源。MIMO-OFDM技术已成为未来无线宽带通信最有效的传输技术之一[ 1, 2]。在MIMO-OFDM系统的接收端,为了抵消信道对发射信号的影响,就必须了解各天线对之间的信道状态信息(Channel state information,CSI),因此对信道的精确估计和对信号的可靠、有效检测是系统检测的重要环节[ 3],是进行译码的基础。
目前,在MIMO-OFDM系统的信道估计研究领域中,信道估计方法一般分为基于导频的估计、半盲信道估计和盲信道估计方法[ 4, 5, 6]三种。近年来,联合半盲信道估计的检测技术[ 5]因在信道状态信息不够准确的条件下具有优越性能而得到迅速发展,其通过发送已知的训练导频序列在接收端进行初始的信道估计,再通过迭代校正信道估计值。当发送有用的数据信息时,利用校正的信道估计结果和信道接收信号进行联合迭代判决更新,最终完成信道估计和检测信息输出。文献[7]的研究结果表明:多天线系统的最大似然(ML)检测算法的复杂度随发送天线数呈指数增长,连续干扰抵消算法(Successive interference cancellation,SIC)虽然降低了复杂度,但其性能较差。文献[8]给出了球形译码算法能取得比垂直贝尔实验室分层空时检测更好的性能。虽然球形译码算法可以用较少的计算量来获得最大似然检测性能,但是也存在着如初始半径的选择、更新半径的选择和迭代次数的确定等问题。文献[9]对基于MMSE(Minimum mean square error)的信道估计算法进行了研究。基于MMSE的信道估计算法虽然可以获得很好的性能,但是其运算复杂度仍很高。文献[10-11]提出了基于期望最大化算法的半盲信道估计算法,其利用算法的叠加信号处理思路来分离和估计出每个收发天线对之间的信道状态信息,然后通过迭代得到估计值,虽然该算法避免了矩阵求逆运算,但在每次迭代时需要更新整个参数集信息,其算法复杂度较高,同时对迭代初值要求也较高。
本文将改进的Grover量子搜索算法与SAGE算法相结合,提出了一种基于量子计算的联合信道估计检测算法,该算法在信道状态信息不够准确的情况下利用已解码信息,通过联合迭代更新,实现信道估计和检测,避免了经典的最大似然检测算法需要搜索格内所有格点对信号检测复杂度的影响,提高了信号检测的有效性。仿真结果表明:该算法性能优于传统的联合估计算法。
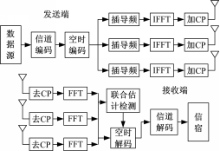
MIMO-OFDM系统模型如图1所示。
MIMO-OFDM系统有NT根发射天线和NR根接收天线,假设信道最大多径时延路径数为L,OFDM符号的子载波数为N,在发射端,信源数据经信道编码后,进行串并转换,分解成多个子数据流,每个子数据流进行映射编码和插入导频,经过IFFT变换后成为时域信号,并插入大于L的循环前缀(CP)以消除ISI。再进行上变频,最后由多根发射天线同时发送出去。在接收端,通过下变频后去除时域信号的循环前缀,并对其进行FFT变换,再经过联合估计检测处理,最终空时解码数据经信道解码后送至信宿,则第m根接收天线接收信息可以表示为:
Y m= XH m+ W m (1)
式中: X为发送向量, X=[ X1, X2,…, 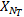


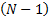
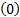
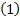
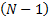

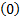
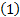
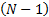
令 F( k)=[ 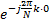

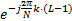
Y j, m(k)=X j(k) F( k) h j, m+W j, m(k) j∈[1, NT] (2)
式中: h j, m为从发射天线j到接收天线m的信道时域响应, h j, m=[ h j, m(0), h j, m(1),…, h j, m( L-1)]T。
则第 m根接收天线接收的信号可表示为不同发射天线发射信号的叠加,即:
Y m( k)= 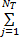
MIMO-OFDM系统中最优检测技术是最大似然( Maximum likelihood, ML)译码检测[ 12],它是将接收信号和所有可能的发射信号的状态进行比较,根据最大似然原理估计出发射信号,但其检测复杂度随着发射天线个数的增加呈指数上升,只适用于理论分析。为了解决这个问题, Grover量子搜索算法被引入到系统检测中,它能够逼近最大似然检测算法的检测性能,其检测复杂度有较大的改善。
1996年, Grover提出了一种用量子计算机搜寻无序数据的快速算法,称为 Grover量子搜索算法[ 13]。该算法在没有关于其结构信息的先验条件下,利用了量子态的叠加性和量子计算的并行性,可以在给定大小为 N的搜索空间中找到满足特定性质的一个元素,算法使搜索问题从经典计算的 O 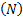
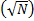
Grover量子搜索算法包括以下5个步骤。
Step1 初始化,产生一个等幅度的叠加态。使 n位量子寄存器的初始状态为 |0 n,0 >,然后对其前 n个分量并行执行量子 Fourier变换,使得 N=2 n个初始态的概率幅一致。
 | (4) |
Step2 完成对判决函数进行受控非门量子比特门计算。
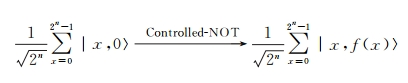 | (5) |
式中: Controlled-NOT量子比特门运算实现 |x, b>→ |x, b f( x) >计算。
Step3 对式(5)结果中的第2个分量做 Z变换操作,从叠加态中标记问题的解:
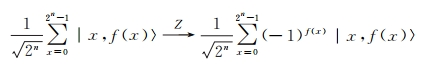 | (6) |
式中: Z变换实现 α|0 >+β|1 >→ α|0 >-β|1 >运算。
Step4 对式(6)结果的第1个分量执行 D变换操作,从叠加态中将问题解的几率幅度进行放大,进行降低非解的几率幅度,其中 D变换的变换矩阵 D= 
d ij=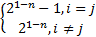 | (7) |
量子态的幅度变化为:
a' i= 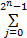
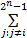
S tep5 重复执行 k=(π 
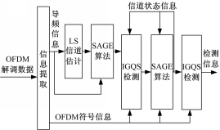
联合估计检测模型如图2所示。联合估计检测技术是将OFDM解调数据进行信息提取,将提取出的导频数据经过LS估计输出初始信道估计信息和SAGE算法的内部迭代环,当达到收敛条件时输出更新后的信道状态信息,然后将其与提取OFDM符号一起进行改进的Grover量子搜索算法(Improved Grover's quantum search algorithm,IGQS)检测和SAGE算法内部迭代环处理,达到收敛条件时输出更新后的信道状态信息,最终经过IGQS检测输出检测数据信息,并将更新后的信道状态信息作为下一符号的初始信道估计信息。循环操作直至整帧数据检测操作完成。
MIMO-OFDM系统在发送数据时,以帧为单位进行数据传输,在每帧帧头都存在一个训练符号子块,接收时将接收码符号分成n+1个子块,第1个子块为已知训练符号子块,其他子块为n个OFDM符号子块。MIMO-OFDM系统经过OFDM解调后,根据每一帧前端已知的块状导频数据,对接收信号进行LS信道估计得到:
H m= X -1 Y m (9)
则接收天线 m的信道时域响应为:
h m= F -1 H m (10)
式中: F为归一化 FFT变换矩阵, F( u, s)= 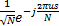
根据SAGE算法原理[ 13, 14],接收信号 Y为不完全数据,发送数据 X为潜在数据, h为待估计量,对于第 k个子载波,在第 m根接收天线上基于 SAGE算法的信道估计如下:
初始化,分别对 j∈ 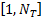
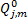 ( k) =X j( k) F( k) ( k) =X j( k) F( k) 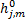 | (11) |
当第r步迭代时,计算j=1+r mod NT,
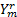
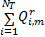
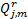
然后更新计算信道冲激响应:
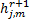 =argmin =argmin 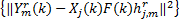 | (13) |
根据最小二乘准则,求解可得:
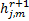
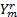
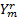
由于系统为恒模调制,将式(14)简化,可以得到更新后的第 j个发射天线和第 m个接收天线之间的信道冲激响应为:

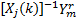
更新中间变量:
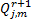 =X j( k) F( k) =X j( k) F( k)  | (16) |
最后对于其他 
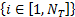
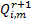 = = 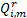 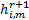 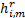 | (17) |
重复SAGE算法的操作,直到达到最大迭代次数时完成迭代过程,至此完成了第0个子块的信道状态信息跟踪,将其作为第1个子块的信道状态信息初值。
首先,在信号检测之前,需要先构建2个量子寄存器,将发送端所有可能发送的序列存储到量子寄存器a,并更新其量子基态的概率幅,使其初值为1/ 

其次,迭代 int( π 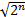
最终迭代完成后,在量子寄存器a的量子基态概率幅中寻找逼近概率1的量子基态,输出对应序列得到结果。
改进Grover量子搜索算法就可以得到第1个子块初始符号估计检测值,再次通过上述的SAGE迭代算法,输出更新后的第1个子块的校正信道状态信息,利用改进的Grover量子搜索算法得到第1个子块符号检测值。循环操作,最终完成n个子块的信道估计和信号检测,即完成整个帧数据的信号检测。
对本文提出的SAGE-IGQS联合估计检测算法设计方案进行系统性能仿真,系统仿真模型参照SCME信道标准,具体参数如表1所示。假设发送天线和接收天线都相互独立,并且一帧内信道参数基本保持不变,分别对系统检测的复杂度、误比特率进行对比。
| 表1 MIMO-OFDM系统仿真参数 Table 1 MIMO-OFDM system simulation parameters |
图3给出了调制方式为QPSK,改进的Grover量子搜索算法和最大似然检测算法在进行单次MIMO-OFDM系统检测过程中搜索次数的比较曲线。仿真结果表明:随着发射天线的增加,似然检测算法搜索次数的增加明显快于改进的Grover量子搜索算法,尤其是在发射天线很多的情况下,这种次数上的增长更加显著。可以看出,基于改进的Grover量子搜索算法在MIMO-OFDM系统检测方案中可以明显改善最大似然检测的复杂度。
 | 图3 单次MIMO-OFDM系统检测中搜索次数的比较曲线Fig.3 Compare of the search numbers in MIMO-OFDM system for single detection |
图4给出了基于理想信道估计的ML检测算法、基于LS信道估计的ML检测算法、基于LMMSE信道估计的ML检测算法、基于MMSE信道估计的ML检测算法和本文提出的SAGE-IGQS联合估计检测算法在设定的仿真参数为表1所示的情况下不同信噪比的误比特率性能曲线。仿真结果表明:在相同LS信道估计下,SAGE-IGQS算法通过SAGE迭代算法对LS估计的信道状态信息进行了校正,使MIMO-OFDM系统检测性能得到了提高,与未结合SAGE算法的ML算法相比,性能有了很大程度的改善。同时,在相同误比特率情况下,本文所提SAGE-IGQS联合估计检测算法性能优于传统的基于LMMSE的ML检测算法;与基于MMSE信道估计的ML检测算法相比,性能有一定改善,但是由于引入了IGQS算法,复杂度显著降低;与理想信道估计下的最大似然检测算法仅平均相差1 dB。
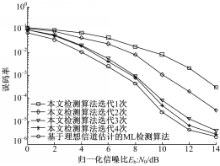
图5给出了在仿真参数设置如表1的情况下,SAGE-IGQS算法误比特率随SAGE算法数的变化曲线图。仿真结果表明,随着迭代次数的增加,系统的误比特率有了明显的下降,其中以前3次迭代所取得的性能增益最为明显。迭代次SAGE算法迭代检测技术在四次迭代后,算法基本趋于收敛。
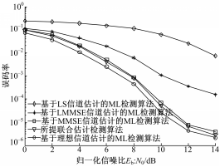 | 图4 不同检测算法下的误比特率性能比较Fig.4 Bit error rate performance of the system with different detection algorithms |
提出了一种基于Grover量子搜索算法结合SAGE算法的联合估计检测算法。算法的主要思想是采用LS对信道进行初估计,利用SAGE迭代过程获得信道状态信息,联合改进的Grover量子搜索算法进行检测,从而达到在MIMO-OFDM系统信道状态信息不够准确的情况下能精确检测的目的。在所设定的仿真参数条件下,对提出的算法进行了仿真分析和性能比较。仿真结果表明:提出的联合估计检测算法优于传统的基于LMMSE和MMSE信道估计的ML检测算法,其性能接近于理想信道估计条件下的最大似然信号检测算法,信噪比损失在1 dB左右。同时,该算法由于引入了改进的Grover量子搜索算法,使检测复杂度有了明显的降低,具有一定的工程实用价值。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|