引用本文
毕晓君, 王珏, 李博. 基于生物地理学优化的雷达正交波形设计算法. 2014, 44(3): 867-873
BI Xiao-jun, WANG Jue, LI Bo. Orthogonal waveform design for radar based on biogeography-based optimization. 吉林大学学报(工学版), 2014, 44(3): 867-873  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于生物地理学优化的雷达正交波形设计算法
毕晓君, 王珏, 李博
哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001

毕晓君(1964),女,教授,博士生导师.研究方向:信息智能处理技术,数字图像处理.E-mail:bixiaojun@hrbeu.edu.cn

基金:国家自然科学基金项目(61175126); 中央高校基本科研业务费专项基金项目(HEUCFZ1209); 高等学校博士学科点专项科研基金项目(20112304110009);
摘要

为了提高MIMO雷达发射信号多相序列的正交性能,提出了基于改进生物地理学优化的雷达正交波形设计算法(POBBO)。该算法首先对生物地理学优化算法(BBO)进行改进,直接采用个体的栖息地适宜度指数(HSI)值来确定迁入迁出率,对其原始确定机制进行大幅简化,在实时反映个体优劣程度的同时,缩短由排序带来的时间损耗。另外,引入分段Logistic混沌映射改进原变异机制,实现对新个体的有效开采。POBBO算法利用改进后BBO算法的栖息地间物种迁移和变异进行信息交互,改善栖息地的HSI值,从而得到具有较好正交性能的多相序列波形。仿真试验结果表明:POBBO算法比其他多相序列波形设计算法在整体上具有明显优势,可以有效地兼顾搜索精度和速度。

关键词: 信息处理技术; 生物地理学优化; 正交波形设计; 分段logistic混沌映射; 迁入迁出率
中图分类号:TN911.73 文献标志码:A 文章编号:1671-5497(2014)03-0867-07
Orthogonal waveform design for radar based on biogeography-based optimization
BI Xiao-jun, WANG Jue, LI Bo
College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China
Fund:
Abstract

To improve the orthogonal performance of polyphase sequences of transmitting signals for Multiple-Input Multiple-Output (MIMO) radar, a modified biogeography-based optimization algorithm, POBBO, is proposed for designing orthogonal waveform of polyphase sequences for radar. In this proposed algorithm, the Biogeography-based Optimization algorithm (BBO) is improved. The Habitat Suitability Index (HSI) for individuals is directly adopted to determine the immigration rate and the emigration rate, which significantly simplifies the original method. This reflects the real-time quality for individuals meanwhile shortens the time loss by sorting. Simultaneously, the piecewise logistic chaotic map is introduced to improve the variation mechanism and achieve the effective exploitation for new individuals. In order to obtain the waveform of polyphase sequences with better orthogonal performance, POBBO utilizes the migration and the mutation among the habitats of BBO to interact and improve the HSI. Numerical experiments show that POBBO is competitive with other waveform design algorithms in terms of search accuracy and speed.

Keyword: information processing; biogeography-based optimization; orthogonal waveform design; piecewise logistic chaotic map; the immigration rate and the emigration rate
0 引言

多输入多输出(multiple input multiple output,MIMO)雷达[ 1]作为一种新兴的有效探测技术,可以有效地提高雷达抗截获性能和对目标的探测性能。如何成功设计良好的自相关和互相关正交码集是MIMO雷达探测技术实现的关键。

为了使多相序列满足正交信号要求,Khan[ 2]利用正交变换对多相序列进行设计,但是该方法不适用于信号个数超过3个或信号码较长时的情况。Deng等[ 3]和刘波等[ 4]分别利用混合模拟退火算法和遗传算法来搜索正交多相信号,但由于在针对该问题的搜索中,无法充分体现原算法的进化特性,致使搜索结果在性能和效率上均未达到较好效果。刘伟等[ 5]提出用混合离散粒子群算法进行正交多相码设计,但算法的结构复杂,可执行性较差且搜索效率提高得不明显。胡亮兵等[ 6]以最小化峰值相关旁瓣为优先准则,采用约束非线性规划设计雷达正交波形,虽然获取了较好的正交性能,但牺牲了搜索速度。Zeng等[ 7]将自相关旁瓣、互相关峰值以及自相关旁瓣总能量和互相关总能量拆分为4个目标,提出了一种多目标正交码信号设计算法,但加大了对信号码集最后的选择复杂度。

生物地理学优化算法(Biogeography-based optimization,BBO)[ 8]是目前求解全局优化问题效果最好的群智能优化算法之一,在收敛精度、速度及稳定性等方面均优于遗传算法等优化算法。其个体采取整数编码且进化过程中采用离散迁移机制,使其在求解离散空间内的优化问题时较粒子群、差分进化等适用于连续问题的优化算法更具有优势,目前在图像识别[ 9]、生产调度[ 10]、运动估计[ 11]、心脏疾病诊断[ 12]、阵列天线综合[ 13]等领域已获得了较为成功的应用。然而,BBO算法自身对个体信息的有效开采和利用能力仍有待提高。为此,本文对BBO算法迁入迁出率的确定机制和变异机制进行了改进,并首次将其应用于MIMO雷达正交多相序列的波形设计中,提出了一种基于改进生物地理学优化的MIMO雷达正交多相序列的波形设计算法(POBBO),可以在有效提高发射信号正交性能的同时兼顾搜索速度。

1 MIMO雷达正交波形设计原理

假设MIMO雷达系统有L根发射天线,每根天线发射正交多相码集中的一个信号,每个信号包含N个子脉冲(即信号的码元长度为N),则信号 s l可表示为如式(1)所示的多相序列。

s l={ s l( n)= 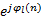, n=1,2,…, N} φ l( n)∈{ φ1, φ2,…, φ M}={0, ,…,( M-1) }, l=1,2,…, L (1)

式中: φ l( n)为信号集中第 l个信号的第 n个子脉冲; M为每个子脉冲可选的相位个数。

对于码元长度为 N,信号数为 L的信号集,可由如式(2)所示的 L×N的相位码矩阵 S表示:

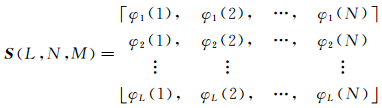(2)

多相序列 s p与 s q间的非周期相关函数可表示为:

C p, q( k)= 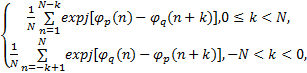p, q=1,2,…, L(3)

式中: k为离散时间符号;当 p=q时, C p, q( k)为多相序列 s p(或 s q)的非周期自相关函数,是信号 p(或 q)经自身匹配滤波器的脉冲压缩输出; C p, q(0)为脉压峰值, C p, q( k, k≠0)为脉压旁瓣;当 p≠ q时, C p, q( k)为 s p和 s q的非周期互相关函数,是信号 p经过信号 q的匹配滤波器后对 q的干扰输出。设计正交多相码等效于在满足 C p, q( k)=0的条件下构建多相码矩阵 S。

2 本文算法

BBO算法通过模拟栖息地之间的物种迁移机制实现寻优过程。其中,栖息地( Habitat)表示优化问题的可能解,栖息地指数变量( Suitability index variabl e, SIV)为解变量,栖息地的优劣程度可以由栖息地适宜度指数( Habitat suitability index, HSI)来衡量。由于 BBO算法仍存在易陷入局部最优及未对个体信息进行充分利用等不足,本文从迁入迁出率的确定机制和变异机制2个方面对 BBO算法进行改进。

在正交多相波形设计问题中,将改进后 BBO算法的栖息地,栖息地指数变量和 HSI分别映射成多相码矩阵、阵内码和正交码优化准则。随机构造多个栖息地作为初始多相码矩阵,通过栖息地之间的物种迁移变异进行信息交互,提高栖息地的物种多样性,改善栖息地的 HSI,进而得到近似正交的多相序列集。

2.1 种群的初始化

为了满足多相序列编码的要求,本文将原BBO的初始个体扩展为矩阵,在可行解空间中随机产生NP个栖息地个体作为初始种群,每个栖息地个体 x中包含 L×N个 SIV,即:

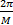
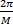
分别对应多相码矩阵中 L×N个子脉冲相位。为了便于编码,提取各子脉冲相位的公因子2 π/M,使 SIV的取值范围为[0, M-1]间的整数,即(0,1,…,( M-1))分别表示多相码相位(0, ,…,( M-1) )。初始栖息地个体的产生方式如下

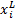
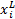
: x i=floor( +random(0,1) ×( - +1)), i=1,2,…, NP (4)

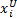
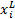
式中: x i为第 i个栖息地个体; 为个体 x i的上界,即 中所有 SIV均取值为 M-1; 为 x i的下界,即所有 SIV均取0; floor(·)为向下取整运算。

2.2 栖息地适应度指数的确定

对于MIMO雷达正交多相序列的波形设计问题,在实际构建多相码矩阵时,只可能近似满足Cp,q(k)=0的条件。通常以自相关旁瓣、互相关峰值以及自相关旁瓣总能量和互相关总能量共同作为衡量多相码正交性能的优化准则,将4项指标的加权总能量作为HSI,如式(5)所示:

E=ω1×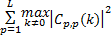+ω2× +ω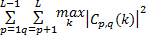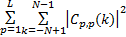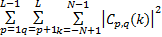3× +ω4× (5)

式中:E为加权总能量;ωi(i=1,2,…,4)为各指标的加权系数。

确定L、M、N后,加权总能量E越小,HSI越高,多相码正交性能越好。

2.3 栖息地迁入率和迁出率的确定

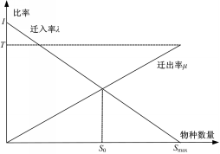
原BBO算法根据迁入迁出率分别确定待迁入栖息地和待迁出栖息地,进而进行物种迁移。其中,栖息地的HSI与其物种数量成正比,且栖息地的物种数量亦与其迁入迁出率间存在如图1所示的线性关系。

图1 BBO算法物种迁移模型Fig.1 Species migration model of BBO

通过对NP个栖息地 x i按照 HSI高低降序排序,可确定 x i的迁入率 λ i和迁出率 μ i,如式(6)所示:

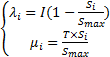(6)

式中:栖息地 x i的物种数量 S i =Smax -i, i=1,2,…, NP; Smax为最大物种数量; I、 T分别为每个栖息地的最大迁入率和迁出率。

然而,通过对栖息地个体的 HSI值进行排序并结合物种迁移模型而获得的迁入迁出率,只能够反映出个体的优劣顺序,而无法有效地获得个体的优劣程度,直接影响对待迁入、迁出栖息地的判断。当个体优劣差距较大或分布不均衡时,原迁入迁出率确定机制很容易对个体的优劣程度造成错误的评估,致使较优个体信息无法得到保留或较差个体过早参与进化。

针对上述问题,在本文提出的 POBBO算法中,直接采用个体的 HSI值来简化确定迁入迁出率,以保证对当前种群中个体信息进行有效利用为前提,在实时反映个体的优劣程度的同时,缩短由对整个栖息地排序而带来的时间损耗。迁入率和迁出率的确定如式(7)所示:

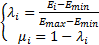(7)

式中: E i为栖息地 x i的 HSI;E min、E max分别为当前种群中 HSI的最高值和最低值。

2.4 迁移机制

在迁移操作中,对于每个栖息地个体 x i,可根据迁入率 λ i决定其是否进行迁移。其中,栖息地 x i的迁入率 λ i越大,表明其 HSI值越低,对应的多相码正交性越差,故被选取为待迁入栖息地的概率越高;反之,若 x i的 λ i越小,其 HSI值越高,当前个体的信息越有机会被保留。

若栖息地 x i被选定进行迁移,则对于 x i中的每个 SIV,根据迁入率 μ i轮盘赌选取待迁出的栖息地 x k,之后从 x k中选取对应的 SIV代替 x i中的 SIV。

2.5 变异机制

栖息地 x i的变异率 m i为:

m i =mmax(1- ) (8)

式中: mmax为栖息地的最大变异率; P i为栖息地 x i的物种概率,可由迁入率 λ i和迁出率 μ i通过式(9)确定; Pmax=arg max P i。

P i=(9)

式中: S i为 x i的物种数量; Smax为最大物种数量。

对于栖息地 x i的每个 SIV,原 BBO算法根据变异率 m i进行随机单点变异。然而,这种简单的变异方式对新个体的开采能力十分有限,具有一定的盲目性和赌博性。尤其是在进化后期当前栖息地个体的 HSI值较高(即 E值较小)的情况下,用随机变异很难勘探出更优个体,反而容易生成更差个体,无疑造成了资源浪费,影响了算法的搜索效率。为此,本文借鉴分段 Logistic混沌映射[ 14]思想,提出分段 Logistic混沌变异机制,利用其高度遍历和随机能力,在局部最优个体的周围生成多个邻域点,帮助当前个体跳出局部最优,实现对新个体的有效开采,努力突破由随机变异带来的搜索瓶颈。 POBBO算法根据变异率 m i,按照式(10)生成混沌序列,之后按照式(11)进行变异操作。

z1( l, j)=floor( M×random(0,1))

z g+1( l, j)=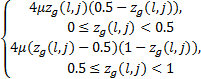(10)

x i( l, j)=(2-2 z i( l, j)) ×x i( l, j)+(2 z i( l, j)-1) ×xbest( l, j), i=1,2,…, NP; l=1,2,…, L; j=1,2,…, N (11)

式中: μ=4; g为迭代次数; x i( l, j)为栖息地个体 x i矩阵中第 l×j个 SIV; xbest( l, j)为当前最好个体的第 l×j个 SIV。

2.6 POBBO算法的实现流程

步骤1 初始化参数NP,L,N,M,m max,S max。按照式(4)随机产生NP个栖息地个体 x i作为初始种群 U={ x i, i=1,2,…, NP},每个 x i中包含 L×N个 SIV。

步骤2 按照式(5)计算每个栖息地 x i的 HSI值。

步骤3 按照式(7)确定栖息地物种的迁入率 λ i和迁出率 μ i。

步骤4 根据 λ i和 μ i,按2.4节方法对栖息地 x i进行物种迁移操作,产生新的栖息地个体 x ' i。

步骤5 按照式(8)确定其变异率 m i,按照式(9)计算栖息地 x ' i的物种概率 P i。

步骤6 按照式(10)生成混沌序列,之后按照式(11)对栖息地 x ' i进行物种变异操作。

步骤7 对变异后新产生的栖息地个体 x ' i与原始栖息地 x ' i进行比较。若 x ' i < x i,则用 x ' i代替原始 x i;否则保留 x i。

步骤8 判断是否满足终止条件,若不满足转到步骤2,否则输出最优栖息地个体 x。

3 仿真试验及结果分析

为了验证本文算法的有效性和先进性,进行了仿真试验,并与文献[ 2, 3, 4, 5, 6]方法进行了比较。试验在 Intel® Pentium® CPU G620 @ 2.60 GHz,内存4.00 GB,主频2.60 GHz的计算机上进行,开发环境为 Matlab R2011 a。

试验参数设置为:发射天线个数 L=4,子脉冲相位个数 N=40,可选相位个数 M=4,种群规模 NP=100, ω i( i=1,2,…,4)的设置参见文献[ 3]。 POBBO算法中最大物种数量 Smax =NP,最大突变率 mmax=0.005。其他算法参数设置分别参见文献[ 2, 3, 4, 5, 6]。

3.1 POBBO算法的有效性验证

用本文的POBBO算法生成的多相码序列集如表1所示。表2为该序列集的非周期自相关旁瓣峰值(Autocorrelation sidelobe peak,ASP)和序列间的非周期互相关峰值(Cross-correlation peak,CP)。

表1 多相序列集 Table 1 Designed polyphase sequence set
表2 序列自相关旁瓣峰值和互相关峰值 Table 2 ASP and CP of the designed sequences

由表2可以得出:采用本文提出的POBBO算法设计的多相序列平均自相关旁瓣峰值为0.1233(-18.18 dB),平均互相关峰值为0.1967(-14.12 dB)。该多相序列集的自相关和互相关函数曲线分别如图2和图3所示。

图2 多相序列的自相关函数Fig.2 Autocorrelation functions of polyphase sequences

图3 多相序列的互相关函数Fig.3 Cross-correlation functions of polyphase sequences

从图2和图3中分别可以看出:由POBBO算法生成的多相序列非周期自相关旁瓣值较低,分布较为均匀,表明信号自身具有良好的脉冲压缩性能;序列之间亦取得较低的互相关值,表明信号之间的脉冲干扰较小。从而证明了POBBO算法设计的多相序列可以获得较好的正交性能。

3.2 本文算法与文献[ 3, 4, 5]中算法的比较

为了验证本文提出的POBBO算法的先进性,将其分别与文献[ 3, 4, 5]中给出的基于群智能(包括SA,GA,PSO算法)的多相序列波形设计算法进行比较。表3为POBBO算法分别与其他3种算法设计生成序列的ASP和序列间的CP的最大值及平均值对比结果,且平均ASP和平均CP随函数评价次数变化的曲线如图4所示。

表3 四种算法生成序列的自相关旁瓣峰值和互相关峰值的最大值和平均值 Table 3 Maximum values and average values of ASP and CP of sequences by 4 algorithms

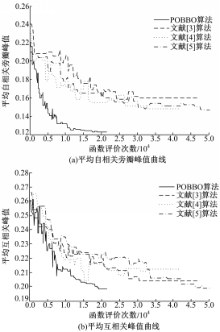图4 四种算法生成序列的平均自相关旁瓣峰值和互相关峰值随函数评价次数变化曲线Fig.4 Average ASP and CP curves of sequences varied with numbers of function Evaluations with 4 algorithms

由表3可以看出:相对于3种算法,POBBO算法无论是在最大值上,还是在平均值上,均可取得最低的ASP和CP。特别是在保证取得较低CP的同时,POBBO算法在ASP上具有明显优势。因此,将ASP和CP两者结合来看,POBBO算法在搜索精度上明显优于其他3种基于群智能的多相序列波形设计算法。

由图4(a)可以看出:在相同函数评价次数下,POBBO算法较其他3种算法能够始终取得较低的平均ASP。由图4(b)可以看出:虽然在进化前期,4种算法的平均CP波动幅度较大,趋势不是很明显,但当函数评价达到17 000次后,POBBO算法较其他3种算法体现出较为明显的优势,能够且最先取得最低的CP值。因此,相对于其他3种算法,POBBO算法能够在最短时间内取得最低的ASP和CP,具有较高的搜索效率,在搜索速度上明显快于其他3种算法。

3.3 与其他多相序列波形设计算法的比较

为了进一步验证POBBO算法的先进性,将POBBO算法与文献[2,6]中给出的目前效果较好的其他多相序列波形设计算法进行了比较,生成的序列自相关旁瓣和互相关峰值如表4所示。

就搜索精度而言,从表4可以看出:POBBO算法与文献[ 2]算法相比取得的平均CP相差无几,但平均ASP明显低于文献[ 2]算法;与文献[ 6]算法相比,POBBO算法可以取得较低的平均ASP,而对于平均CP,POBBO算法不如优化变量自由度较大的文献[ 6]。就搜索速度而言,由文献[ 6]可知,对于相同信号数目和码长的正交波形设计,文献[ 2, 6]算法的计算时间慢于文献[ 4]中GA算法,而由图3和图4可以看出:POBBO算法的搜索速度较文献[4]算法要快很多,故可以得出,POBBO算法在搜索速度上要优于文献[ 2, 6]这两种算法。综合搜索精度和速度两方面指标,POBBO算法较文献[ 2, 6]算法均体现一定程度上的性能优势。

表4 POBBO与其他2种算法生成序列的平均自相关旁瓣峰值和互相关峰值 Table 4 Average ASP and CP of sequences by POBBO and other 2 algorithms dB
4 结束语

通过直接利用个体的HSI值确定迁入迁出率及采用分段Logistic混沌变异机制改进了原BBO算法,并将其引入到MIMO雷达正交多相序列的设计中,提出了一种基于改进生物地理学优化的MIMO雷达正交多相波形设计算法(POBBO)。利用栖息地个体间物种的迁移和变异机制实现信息交互,改善栖息地的HSI,从而搜索全局最优解。试验结果表明:POBBO与目前效果较好的其他多种多相序列波形设计算法相比,在搜索精度和速度上均具有明显优势,可以使雷达发射信号得到较低的自相关旁瓣和互相关值,从而获得较好的正交性能,在实际应用中具有一定的推广价值,且在成功解决雷达正交波形设计问题的同时,使原BBO算法的应用领域得到了扩展。

The authors have declared that no competing interests exist.

参考文献
[1] He H, Stoica P, Li J. Designing unimodular sequence sets with good correlations-Including an application to MIMO radar[J]. IEEE Transactions on Signal Processing, 2009, 57(11): 4391-4405. [本文引用:1] [JCR: 2.813]
[2] Khan H A, Zhang Y Y, Ji C L, et al. Optimizing polyphase sequences for orthogonal netted radar[J]. IEEE Signal Processing Letters, 2006, 13(10): 589-592. [本文引用:8] [JCR: 1.674]
[3] Deng H. Polyphase code design for orthogonal netted radar systems[J]. IEEE Transactions on Signal Processing, 2004, 52(11): 3126-3135. [本文引用:6] [JCR: 2.813]
[4] 刘波, 何子述. 基于遗传算法的正交多相码设计[J]. 电子测量与仪器学报, 2008, 22(2): 62-66.
Liu Bo, He Zi-shu. Genetic algorithm based MIMO radar polyphase code design[J]. Journal of Electronic Measurement and Instrument, 2008, 22(2): 62-66. [本文引用:6] [CJCR: 3.5328]
[5] 刘伟, 贺正洪, 张启亮, 等. 基于混合离散粒子群算法的正交多相码设计[J]. 现代防御技术, 2009, 37(6): 77-82.
Liu Wei, He Zheng-hong, Zhang Qi-liang, et al. Polyphase orthogonal code design based on hybrid particle swarm optimization[J]. Modern Defence Technology, 2009, 37(6): 77-82. [本文引用:5] [CJCR: 0.1747]
[6] 胡亮兵, 刘宏伟, 吴顺君. 基于约束非线性规划的MIMO雷达正交波形设计[J]. 系统工程与电子技术, 2011, 33(1): 64-68.
Hu Liang-bing, Liu Hong-wei, Wu Shun-jun. Orthogonal waveform design for MIMO radar via constrained nonlinear programming[J]. Systems Engineering and Electronics, 2011, 33(1): 64-68. [本文引用:9] [CJCR: 0.499]
[7] Zeng X N, Zhang Y S, Guo Y D. Polyphase coded signal design for MIMO radar using MO-MicPSO[J]. Journal of Systems Engineering and Electronics, 2011, 22(3): 381-386. [本文引用:1] [JCR: 0.384] [CJCR: 0.4318]
[8] Simon D. Biogeography-based optimization[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(6): 702-713. [本文引用:1] [JCR: 4.81]
[9] Chatterjee A, Siarry P, Nakib A, st al. An improved biogeography based optimization approach for segmentation of human head CT-scan images employing fuzzy entropy[J]. Engineering Applications of Artificial Intelligence, 2012, 25(8): 1698-1709. [本文引用:1] [JCR: 1.625]
[10] Roy P K. , Ghoshal S P, Thakur S S. Biogeography based optimization for multi-constraint optimal power flow with emission and non-smooth cost function[J]. Expert Systems with Applications, 2010, 37(12): 8221-8228. [本文引用:1] [JCR: 1.854]
[11] Zhang P, Wei P, Yu H Y. Biogeography-based optimization search algorithm for block matching motion estimation[J]. IET Image Processing, 2012, 6(7): 1014-1023. [本文引用:1] [JCR: 0.895]
[12] Ovreiu M, Simon D. Biogeography-based optimization of neuro-fuzzy system parameters for diagnosis of cardiac disease[C]∥Proceedings of the 12th annual conference on Genetic and evolutionary computation, New York, USA, 2010: 1235-1242. [本文引用:1]
[13] Singh U, Kamal T S. Synthesis of thinned planar concentric circular antenna arrays using biogeography-based optimization[C]∥2012 1st International Conference on Emerging Technology Trends in Electronics, Communication and Networking, Surat, Gujarat, India, 2012: 1-5. [本文引用:1]
[14] 范九伦, 张雪峰. 分段Logistic混沌映射及其性能分析[J]. 电子学报, 2009, 37(4): 720-725.
Fan Jiu-lun, Zhang Xue-feng. Piecewise Logistic chaotic map and its performance analysis[J]. Acta Electronica Sinica, 2009, 37(4): 720-725. [本文引用:1] [CJCR: 0.686]