张洁(1981),女,博士研究生.研究方向:地震勘探信号处理.E-mail:z_jie@jlu.edu.cn
针对传统时频峰值滤波(TFPF)算法在消减地震勘探资料中的随机噪声时,容易引起有效信号波峰和波谷处的误差问题,提出了平行径向道TFPF方法。该方法将地震信号从炮检距-双程旅行时域变换到视速度-双程旅行时域后,沿时空域径向道方向进行TFPF。讨论了不同径向道轨线对TFPF无偏估计的影响,并对人工合成的地震记录进行了仿真试验,将沿不同轨线的平行径向道TFPF与传统TFPF结果进行比较。结果表明:所选轨线平行于同相轴或与之夹角很小时,可使信号在一个TFPF时窗内更好地满足无偏估计的条件,从而减小了滤波后波峰及波谷处的误差,使本文方法具有更好的保幅性,其信噪比较传统TFPF算法提高了5 dB左右,通过对实际地震记录的仿真,证明了该方法的实用性。
Traditional Time-frequency Peak Filtering (TFPF) usually causes errors at peaks and valleys of valid signal. This study proposed a parallel Radial Trace Transform (RTT)-TFPF with x-interpolation method to reduce these errors. The proposed method uses TFPF to eliminate noise after mapping seismic signals from coordinates of offset and traveltime to those of apparent velocity and traveltime, namely filtering the signals along the direction of the radial trace in the time-space domain. The effect of the different slope of radial trace on the unbiased estimation of TFPF was discussed. Simulation experiments of synthetic seismogram were carried out to compare the traditional TFPF and the RTT-TFPF with different slopes. The results show that when the selected radial traces and events are parallel or the angles between them are small, the proposed method can make the signals better meet the condition of unbiased estimation in one window length, reduce the errors of the peaks and valleys of filtered signal, and improve the property of amplitude-preservation, the SNR of the proposed method can increase about 5 dB.
在地震勘探资料中,有效信号往往被湮没在强随机噪声中,阻碍信号中有效信息的恢复,影响偏移成像和解释工作。因此,将有效信号从低信噪比的地震资料中无损失地恢复出来具有重要意义。
时频峰值滤波(Time-frequency peak filtering,TFPF)算法是Boashash和Mesbah于2004年提出的一种新的基于时频分析理论的信号增强算法[ 1]。该方法是一种瞬时频率估计算法,其原理是将含有噪声的信号通过频率调制,使其成为解析信号的瞬时频率,并利用Wigner-Ville分布(Wigner-Ville distribution,WVD)的峰值估计出有效信号。在实际信号处理过程中,由于信号的非线性,通常采用伪Wigner-Ville分布(Pseudo wigner-ville distribution,PWVD),即加窗的Wigner-Ville分布进行估计。时频峰值滤波后,有效信号得到增强,随机噪声得以抑制。TFPF算法已成功地应用于新生儿的脑电信号处理,并能够从低信噪比的记录中恢复出有效信号。
2005年金雷等[ 2]首次将TFPF应用于地震资料噪声的抑制中,其结果表明,增强了反射信号,有效抑制了随机噪声。林红波等[ 3]将该算法应用于实际地震资料随机噪声的抑制中,也取得了较好的滤波效果,并指出TFPF滤波能够将有效信号从信噪比较低的地震勘探记录中恢复出来[ 4]。而在TFPF滤波中,无偏窗长的选择影响信号的恢复和去噪的效果。林红波等又讨论研究了时窗函数,提出了最优窗长[ 5]和可变窗长时频峰值滤波算法[ 6],在抑制数据中随机噪声的同时,减小了TFPF的滤波误差。然而,这些传统的TFPF滤波是一维的抑制噪声算法,在处理二维地震勘探记录时,其输入信号只是时间的函数,即对每道信号作一维TFPF,忽略了有效信号和随机噪声道与道之间的空间特性差异。为此,吴宁等[ 7]提出了一种径向道时频峰值滤波算法,可以处理二维地震信号,将径向道与TFPF相结合,取得了较好的滤波效果。
本文在此基础上提出了平行径向道TFPF算法,并对不同径向道TFPF结果与传统TFPF结果进行了比较。结果表明:选择与同相轴平行或夹角很小的径向道轨线进行TFPF,可使一个窗长内信号更好地满足线性的条件,从而提高滤波后信号的振幅保真度。
地震记录中的有效信号通常是非平稳的确定性信号,其地震记录模型可表示为[ 1]:
s(t)=x(t)+n(t)=∑xk(t)+n(t) (1)
式中:xk(t)为带限的确定性信号,其频谱可以是重叠的;n(t)为加性的随机噪声。
对含噪记录s(t)进行频率调制,使s(t)成为调制后的解析信号z(t)的瞬时频率,z(t)可表示为:
z(t)= exp(j2 πμ 
式中:μ为调制系数。
再进行瞬时频率(Instantaneous frequency,IF)估计。为了方便实现,采用信号的WVD峰值进行IF估计。根据解析信号WVD的峰值恢复出待测信号:
 (t)= (t)= 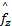 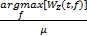 | (3) |
式中:Wz(t,f)为z(t)的WVD,可表示为[ 1]:
Wz(t,f)= 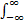


由WVD的性质可知,z(t)的WVD峰值是解析信号瞬时频率的无偏估计。为了满足TFPF的无偏估计,瞬时频率必须是时间的线性函数。而地震信号并非是时间的线性函数,因此,采用加窗的PWVD进行TFPF,以保证TFPF对有效信号的无偏估计[ 1, 8]。
PWVD可表示为[ 1]:
Wz(t,f)= 


式中:h(τ)为矩形窗函数,其大小的选择由信号的线性程度和随机噪声的强度决定,最优窗长的选择在文献[ 4]中已有研究,其公式如下:
L≤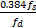 | (6) |
式中: fs为采样频率; fd为有效信号的主频。
对给定的采样频率,其最优L只由 fd确定,主频不同,其窗长的大小也不同[ 6]。由于地震信号的非线性,即使选择最优窗长,窗内的信号也无法完全达到理想的线性,所以引入了径向道变换,以提高窗内信号的线性度。
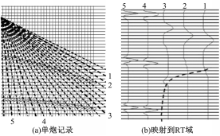
径向道变换(Radial trace transform,RTT)最早主要用于偏移成像[ 9],随后被应用于地震记录相干噪声的去除中[ 10, 11, 12, 13, 14, 15]。它是一种地震道集的映射算法,该算法将地震道振幅从炮检距-双程旅行时域变换到视速度-双程旅行时域。其原理如图1所示。
图1(a)是在地震的单炮记录中(包含3条同相轴)建立的扇形径向道轨线,其中选取了5条有代表性的轨线,并将其映射到RT域中(见图1(b))。
由图1可知,当所选取的轨线平行穿过地震同相轴(轨线1),或与其夹角很小时(轨线2),其映射到RT域时,地震波波形的延续时间变长,频率降低;当所选轨线与同相轴的夹角较大时,其RT域的波形延续时间变化不大,频率几乎不变(见图1(a)中轨线4和轨线5)[ 12, 13];而对随机噪声却不存在这种变化。根据变换域的这一特性,若沿轨线1和轨线2进行TFPF,能使信号更好地满足最优窗长内近似线性程度,减小因信号的非线性而导致的误差。
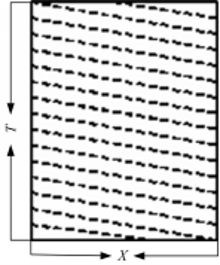
在径向道变换中,根据噪声的不同,存在3种径向道类型:扇型、倾角型和反倾角型[ 10]。但是,这3种径向道类型都是径向道变换原点一旦确定,其径向道就被确定,而在这些类型的径向道变换中,大多数径向道与同相轴夹角较大,根据径向道变换原理可知,只有沿轨线1和轨线2进行径向道变换,才能最大限度地满足在变换域中沿径向道变换后,信号呈低频、信号的线性度得到最大限度提升的要求,因此,在笔者的算法中采用平行的径向道进行TFPF滤波(见图2)。即在炮检距-双程旅行时域中根据同相轴的走向选定一条与其平行的径向道轨线,并按一定的步长,平行移动轨线并采样。
平行径向道TFPF算法步骤如下:
(1)对给定的地震资料进行识别并预估其同相轴大致的斜率,确定径向道轨线斜率。
(2)设定步长,对地震资料进行平行扫描,并采样。
(3)对采样后的信号进行调制,并估计瞬时频率,用PWVD的峰值估计出待测信号。
(4)对TFPF后的信号进行径向道反变换。
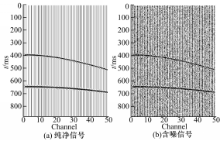
采用两个水平界面的人工合成共炮点地震记录进行仿真试验。记录选用25 Hz的Ricker子波,最小偏移距为零,最大偏移距为500 m,道间距为10 m,实际采样间隔为2 ms,记录长度为1 s(见图3)。图3(a)为具有两个同相轴的纯净信号记录,图3(b)为加入-5 dB噪声的含噪记录。
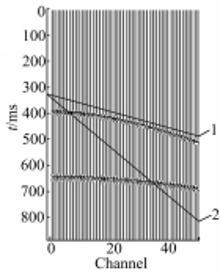
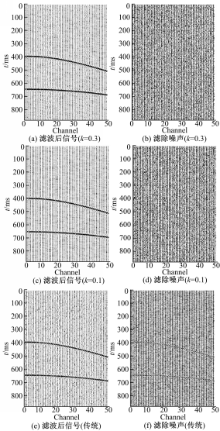
利用边缘检测估计出同相轴大致的倾斜角度,根据人工合成地震记录中浅层同相轴的方向,选择与浅层同相轴大致平行的轨线以及与同相轴存在较大角度的轨线(见图4)。图4中,轨线1的斜率k=0.3,轨线2的斜率k=0.1,分别以这两条斜率的轨线对地震记录进行平行扫描并采样,采样后的信号经TFPF,其结果如图5(a)和图5(c)所示。根据式(6)可得最优窗长为7,因此,滤波所选窗长均为7,设定的扫描步长为时间采样间隔。图5(e)为传统TFPF结果。图5(b)(d)(f)均为滤波后去除的噪声。
从图5中可以看出,图5(a)(c)(e)的去噪效果区别不大,但在传统TFPF后的噪声中能够明显看到残留的信号(见图5(f)),沿斜率为0.1的径向道TFPF后的噪声中也能看到少许的信号残留(见图5(d)),而在斜率为0.3的径向道TFPF后的噪声中几乎看不到信号(见图5(f)),这说明,传统的TFPF对信号的能量有一定的衰减,径向道变换后TFPF能改善信号能量的衰减问题。由于径向道轨线为射线,同相轴为双曲线,因此,在合成地震记录的前几道与轨线有一定的夹角,信号仍有部分能量的衰减。
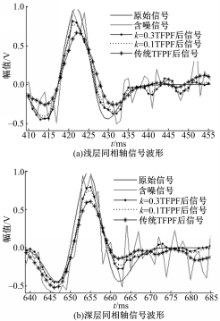
图6为单道信号波形的比较。其中图6(a)和图6(b)分别为第22道信号浅、深两个同相轴上的信号波形图。
由图6可以看出:与传统TFPF相比,采用径向道TFPF的信号,其滤波后的波形幅值有较大的提高。而且当所选径向道轨线( k=0.3)与同相轴近似平行或夹角很小时,其滤波后的信号幅值保持较好,能量损失较少,而所选轨线( k=0.1)与同相轴存在较大的夹角时,幅值的衰减较大,能量的损失也较大。由此可以看出:选择合适的径向道轨线进行TFPF,能够更好地满足线性瞬时频率的条件,其滤波后波形幅值比传统TFPF及沿轨线与同相轴夹角较大的轨线TFPF有较大的提高。
本文对信噪比(Signal-to-noise ratio,SNR)不同的人工合成共炮点地震记录,分别采用传统TFPF和平行径向道( k=0.3)TFPF进行处理,并对滤波后地震记录的SNR进行比较(见表1)。
| 表1 不同TFPF后的SNR Table 1 SNR of different TFPF dB |
由表1可知:对于不同SNR的地震记录,采用平行径向道TFPF后记录的信噪比均比采用传统TFPF后记录的信噪比提高5 dB左右,有效信号得到了较好的恢复。
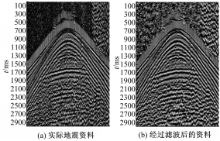
再将平行径向道TFPF方法应用于实际地震资料的处理中(见图7),图7(a)为3 s及168道实际共炮点地震资料;图7(b)为经平行径向道TFPF处理后的结果。从图7(b)可以看出:反射同相轴变得连续、清晰,一些被湮没在噪声中的同相轴也被恢复出来。对于实际地震资料,平行径向道TFPF能得到较好的效果。
利用信号和噪声的空间特性差异,提出了一种平行径向道TFPF算法。试验结果表明:当选择平行或与同相轴夹角很小的径向道轨线进行TFPF时,使径向道变换后的有效信号线性度提高,能更好地满足TFPF无偏估计的条件,与传统TFPF相比,平行径向道TFPF降低了滤波后有效信号在波峰和波谷处的偏差,具有更好的保幅性,使含噪记录中的噪声得到了抑制,有效信号得到增强,在实际的地震资料处理中,该方法也得到了较好的处理效果。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|