汽车轨迹规划及智能决策是实现汽车智能化的关键技术之一,其主要任务是依据环境感知系统处理后的环境信号以及先验地图信息,在满足汽车行驶诸多约束的前提下,以某性能指标最优为目的,规划出车辆的运动轨迹^{[ 1, 2]}。

目前,国内外学者和工程技术人员从许多不同的角度对汽车轨迹规划问题进行了广泛的研究。基于搜索思想的规划方法是其中之一,这类方法源自机器人学,思路是首先建立服务于不同规划方法的环境描述,称之为工作空间(Working space),如位置空间^{[ 3]}或者是速度空间^{[ 4]}。在工作空间中,不被障碍物占据的空间为自由空间。算法在自由空间上进行搜索并根据约束条件以及优化目标决策出最终轨迹。文献[3]提出了一种“状态-时间-空间”法。已知静态以及动态障碍物速度,在以时间为第三维的工作空间中,以规定时间间隔为步长进行搜索。在每个时间点上,均以二维平面处理规划问题。文献[5]加入了运动学和动力学约束条件,使得该算法可以应用在汽车上。该类方法对不同动态环境适应性强,但每个周期得到的轨迹均为局部最优轨迹。另一类是基于设计思想的规划方法。该类方法通常以参数化的曲线,如螺旋线^{[ 6]}、多项式^{[ 7]}表达轨迹,用初始点、终止点状态以及其他约束条件(如碰撞规避)来确定参数选择范围,最后根据优化目标确定参数的值。文献[8]提出的基于六次多项式的轨迹规划方法为这类方法的典型代表。文献[6-8]所述方法优点在于可以在满足汽车动力学和运动学约束并在已知终点状态的前提下得到全局最优轨迹。但该算法对终点处汽车速度、加速度等信息的需求通常情况是不能被满足的。先前研究^{[ 9]}利用简单动力学模型为轨迹发生器,解决未知终点状态的局部动态轨迹规划问题,但每个动态规划周期决策出的局部最优轨迹并不一定为全局最优解。

先前研究^{[ 10]}利用三次多项式生成全局最优轨迹,获得最优前轮转角,据此进行局部动态规划与决策。但存在如下主要问题:①只针对直道,对弯道不具有适用性;②对换道过程后半段进行直线近似,没有考虑当前状态对换道后半程车辆动力学的影响。本文在先前研究^{[ 10]}的基础上,针对问题①利用不同终点约束表征不同道路条件下的换道行为,具有普遍适应性,并以此为对象进行研究;针对问题②利用三次多项式表征速度不变情况下换道过程的完整路径,将当前时刻车辆状态对后续换道过程车辆动力学的影响考虑进来。最后通过在Matlab/Simulink环境下对本文算法的有效性进行了验证。

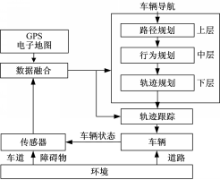
汽车自主行驶技术是实现汽车无人驾驶的关键技术之一。通常情况下,汽车自主行驶任务可以分为三层,如图1所示,每层执行不同任务,包括宏观路径规划,中观行驶行为规划和微观轨迹规划。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 车辆分层决策架构Fig.1 Architecture of hierarchical decision-making framework

宏观路径规划在已知电子地图、路网以及宏观交通信息等先验信息下,根据某优化目标得到两点之间的最优路径。完成路径规划的传感信息主要来自于GPS定位信息以及电子地图。中观行驶行为规划是指根据主车感兴趣区域内道路、交通车等环境信息,决策出当前时刻满足交通法规、结构化道路约束的最优行驶行为。动态规划的行驶行为序列组成宏观路径。行为规划的传感信息主要来自车载传感器如雷达、照相机等,用以识别道路障碍、车道线、道路标识信息和交通信号灯信息等。

微观轨迹规划是指在当前时刻,以完成当前行车行为为目标,考虑周围交通环境并满足不同约束条件,根据最优目标动态规划决策出的最优轨迹。同时,车辆的动力学约束也会在下层得到体现。微观轨迹规划除了必要的外部环境信息外,还需要对主车状态信息进行测量或估计。

在该分层决策架构下,上层规划是面向宏观交通的离线规划,不同优化目标下的宏观规划已经得到比较好的研究,本文不做赘述。本文研究重点是在给定离线规划路径下,对中观行驶行为进行抽象,并针对微观轨迹规划问题提出了考虑全局最优性的动态规划算法。

完成路径需要一系列的行驶行为。常见行驶行为包括换道、保持车道、减速避让、超车、道路交叉口、停车等。实际上,在结构化道路上发生的安全、合法的行车行为,根据该行驶行为与车道的关系可以分为换道和车道保持两种基本驾驶行为:换道指换入不同车道;车道保持指保持在当前车道。

在车道保持命令下,汽车不离开当前所在车道。该情况下的轨迹规划问题仅针对纵向的速度进行规划,不涉及横向规划,其横向轨迹由道路线决定。车辆纵向轨迹规划相对比较简单,现已被广泛应用,如自适应巡航系统。综上,本文提出将微观轨迹规划的研究抽象为不同道路条件下的换道行为研究。

对任意换道行为,终点约束由目标航向角和目标偏移量两部分组成。理想换道结束时,汽车应处于车道中心线位置且汽车航向角与目标车道中心线方向相同。即换道行为结束时目标航向角与目标偏移量均必须满足相应的约束。

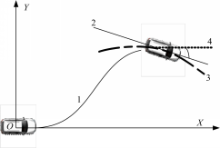
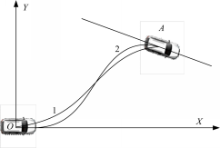
以汽车当前时刻质心为原点,建立以汽车行驶方向为 X轴的大地坐标系 XOY,如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 目标航向角Fig.2 Target orientation

曲线1为完成换道行为的诸多轨迹之一。直线2是目标车道中心线(直道)或者是车道中心线切线(弯道),曲线3为弯道车道中心线。目标航向角为直线2与当前时刻所建立的大地坐标系 X轴的夹角。满足目标航向角的含义是完成换道行为时汽车航向与目标车道方向保持一致。

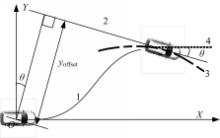
如图3所示,原点(汽车质心所在点)到直线2的距离为目标偏移量。满足目标偏移量的含义是完成换道行为时,汽车质心位置处于目标车道中心线上。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 目标偏移量Fig.3 Target offset

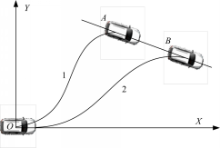
定义完成换道时刻,汽车质心与车道中心线的重合点为换道切入点。显然,换道切入点不唯一。以直道为例,如图4所示,轨迹1、轨迹2的切入点分别是 A、 B,但轨迹1、2均可以实现换道行为。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 不同切入点Fig.4 Different entry points

另外,能够到达同一换道切入点的轨迹也不唯一。同样以直道为例,如图5所示,轨迹1、2的换道切入点都为 A,但轨迹1、2为不相同轨迹。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 同一切入点、不同轨迹Fig.5 Different trajectories under the same entry point

动态轨迹规划中,传统方法通常是基于局部最优目标决策出当前周期的最优轨迹。但是,汽车动力学响应可以表述为如下所示的一般形式:

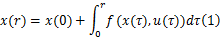
式中: x(0)为当前时刻车辆状态; f为车辆动力学特性方程; u为系统输入。

可见,汽车在未来 r时刻的动力学响应 x( r)与当前时刻的状态 x(0)是有直接关系的,所以局部最优轨迹并不一定是全局最优轨迹,但传统方法并没有考虑这点。为了解决该问题,本文将规划过程分为两步:①全局最优参考轨迹生成;②考虑全局最优性的局部轨迹规划及决策。本文以换道过程中最大侧向加速度表征汽车舒适性;以换道行为耗费时间表征汽车效率;以“时间-空间”坐标系下预估轨迹是否碰撞表征安全性。全局最优参考轨迹以舒适性和效率为评价指标;而局部轨迹规划将结合安全性决策出最终轨迹。

3.1 全局最优参考轨迹生成

换道行为中汽车轨迹由行驶路径和行驶速度两部分组成。若假设换道过程行驶速度不变或变化较小,则换道行为完全由行驶路径决定。汽车具有连续的侧向加速度,固可用三次多项式表达行驶路径:

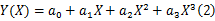
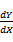
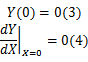
由此多项式确定的坐标( X, Y)表征汽车质心坐标,而( X, )则表征质心坐标为 X时汽车航向角的正切坐标。在所建立坐标系 XOY下,汽车初始的质心坐标和航向均为零,即需要满足如下约束条件:

由式(4)(5)可以确定:

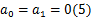
另外,设完成换道行为瞬时,在坐标系 XOY下汽车质心坐标为( X_f, Y_f)。根据终点目标航向角约束可以得到:

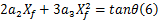
根据终点偏移量约束,可以得到:

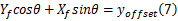
( X_f , Y_f)为汽车行驶轨迹上的点,故满足:

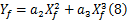
根据先验电子地图信息和任务信息,在微观决策层,目标航向角和目标偏移量均为已知量。联立方程(7)(8)(9),有4个未知数、3个方程,则可用 X_f表示 Y_f、 a₂、 a₃,可得:

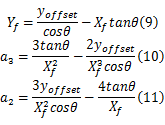
这样式(3)变化为由终点坐标 X_f确定的三次多项式。于是,在速度一定的情况下,三次多项式表达路径由终点坐标 X_f唯一确定,不同 X_f会产生换道切入点不同的轨迹。

显然,最大侧向加速度越大,汽车舒适性越差;而耗费时间越久,则汽车效率越低。为了弥补两个指标在数量级上的差异,对两者均进行无量纲归一化处理,得最终评价指标为:

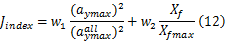
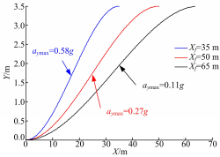
本文中取 w₁ =w₂ =0 .5,图6为在完整直道换道(目标偏移量为3.75 m,目标航向角为0)工况、不同车速下,评价指标在变量 X_f下的变化曲线。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 评价指标与换道纵向距离 XfFig.6 Index and longitudinal lane change distance Xf

在车速确定(以 u=20 m/s为例)时,不同 J_index对应轨迹如图7所示,图中 g=9.8 m/s²。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 不同评价指标的轨迹Fig.7 Different trajectories according to different indexes

3.2 局部轨迹规划

上节已得出全局最优轨迹,但没有考虑交通车对主车的影响。如果按照最优轨迹行驶,主车和交通车有可能发生碰撞,安全性无法保证。本节以先前研究^{[ 10]}为基础,首先根据交通车轨迹预估建立包含“时间”“空间”信息的搜索空间;随后以二自由度车辆动力学模型为轨迹发生器,得到当前状态、不同输入所产生的轨迹簇;最后以全局最优轨迹为参考轨迹,决策出最终轨迹。

3.2.1 交通车轨迹预估以及搜索空间建立

对汽车行驶交通环境中交通参与物位置和运动状态的估计是进行汽车轨迹规划的前提,也是保障汽车安全行驶的关键。交通车的动力学方程同样可用式(1)表达。

虽然通过适当传感可以获取交通车当前时刻的初始状态值 x(0),且状态方程 f也可通过经验获得,但状态方程的输入 u是无法确定的,所以未来的行驶轨迹并不确定,因此估算交通车的行驶轨迹只有概率学和统计学上的意义。然而在实际情况下,大多数车在大多数时候都遵循基本的交通行驶模式,因此本文中合理地假定,在较短的动态规划周期内,交通车保持当前状态(速度和方向)不变,并在此前提下对其未来轨迹进行估算。如式(13)所示,很显然轨迹估算的周期越短,该假设也就越合理。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 安全轨迹示意图Fig.8 Illustration of safe trajectory

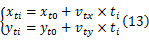
建立以主车规划时刻质心为坐标原点,主车行驶方向为 x轴的笛卡尔坐标系。通过“采样”将不同时刻不同交通车的位置投影到坐标平面中,如图8所示,所有预估轨迹共同组成同时包含“时间”与“空间”信息的搜索空间。通过这样的方式,在一个规划周期内,将动态环境的时间变量转化为静态环境的空间变量。

对于主车任一轨迹 L,若任意时刻、任意交通车,均有:

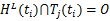
则轨迹 L为安全轨迹。其中 H^L( t_i)与 T_j( t_i)分别为主车和交通车 j在 t_i占据空间的集合。所有安全轨迹组成“待决策轨迹簇”。

3.2.2 基于车辆稳态转向特性的轨迹描述及验证

基于精确和高效相结合原则,本文采用稳态车辆运动学解析表达式的方法表达车辆的行驶轨迹簇。根据文献[11]中的二自由度车辆稳态转向模型得到车辆稳态横摆角速度:

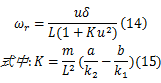
若车辆初始位置为 X₀、 Y₀、 θ₀,那么在 t时刻后,车辆的状态可以解析地表达为:

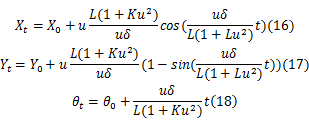
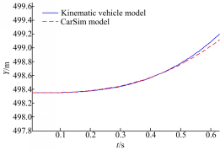
该解析表达式表达的是汽车在给定速度下,对应于不同的转角输入其运动学的响应,可以较为准确地反映车辆的运动轨迹,而且计算效率高、实时性好。基于该理论生成轨迹并与CarSim模型进行对比,对比结果如图9所示。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 行驶轨迹对比Fig.9 Trajectory comparison

图9表明,在0.5 s以前,稳态动力学模型与CarSim模型保持较高的一致性,满足轨迹规划的精度要求。

3.2.3 轨迹决策

根据3.2.2所述的轨迹发生器,可以得到在当前状态不同输入下的待决策轨迹簇。利用指标 J_opt表征每条轨迹与全局最优轨迹的相近程度。其中:

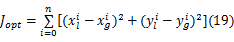
式中:下角标l代表局部规划轨迹;下脚标g代表全局最优轨迹;上角标 i代表不同的离散时刻。

显然,指标 J_opt最小时,局部规划轨迹与全局最优轨迹最接近,即为最优轨迹。由于交通车的位置、速度是动态变化的,所以上述规划算法也为动态规划。

特别地,本文中每个动态规划周期中规划轨迹的时间长度与实际跟踪轨迹的时间长度并不相等,如图10所示。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 规划轨迹与跟踪轨迹Fig.10 Planned trajectories and tracked trajectories

规划轨迹时间长度 t_p越长,完整轨迹的跟踪难度越低,且安全性越高;但若交通情况复杂,周围交通车较多,则不易找到解,规划方法完备性不好。规划轨迹时间长度 t_p越短,规划方法完备性越好,局部最优性越强,但对未来影响考虑不足,全局最优性差。另外,本文中 t_p大小还受限于稳态动力学模型描述轨迹精度。 t_p太大会导致规划轨迹与实际轨迹相比误差太大,是没有意义的。跟随轨迹时间长度 t_track越长,轨迹跟踪式累计误差越大, t_track越短,跟踪精度越高,但计算代价较大,实时性不好。

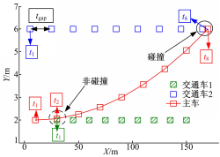
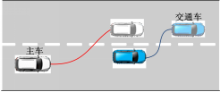
仿真场景如图11所示,仿真中主车以50 km/h速度行驶,交通车以较慢的速度(36 km/h)行驶,显然主车换道过程会受到交通车行驶行为的影响。

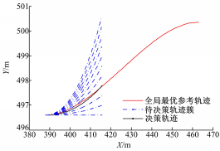
图12为某周期动态规划、决策仿真结果。在待决策轨迹簇中,与全局最优参考轨迹最为接近的为最终决策轨迹。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 仿真场景示意图Fig.11 Illustration of simulation scenario

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 单周期轨迹规划、决策仿真结果Fig.12 Simulation result of trajectory planning and decision in one period

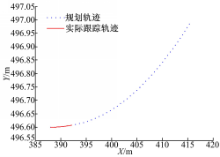
图13为汽车实际轨迹与全局最优参考轨迹的对比。实验结果表明,仿真开始主车不受交通车影响,实际轨迹与参考轨迹重合度很高;但后半段,由于交通车影响,两者出现差异,证明局部动态规划可以规避对交通车的碰撞。

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 仿真轨迹与全局最优参考轨迹Fig.13 Optimal reference trajectory

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 动态规划轨迹与轨迹跟随Fig.14 Dynamically planned trajectory and trajectory tracking

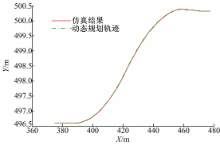
图14为实际轨迹与规划轨迹的对比,仿真结果不仅表明轨迹跟随控制算法有效,而且表明基于车辆动力学方法产生的轨迹能够被很好地跟踪。

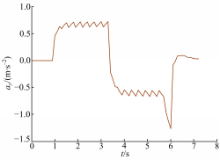
图15为换道过程中车辆侧向加速度的变化。仿真结果表明整个换道过程其值均在合理范围内。

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 侧向加速度Fig.15 Lateral acceleration

(1)针对智能车轨迹规划问题,提出一种车辆行驶轨迹规划的分层决策架构。在该架构下,利用终点约束表征任意道路条件下的行车行为。在假设速度不变的前提下,利用三次多项式描述完整换道轨迹,并根据评价指标决策出全局最优轨迹。以简单车辆动力学模型作为轨迹发生器,在交通车轨迹预估基础上,基于“时间-空间”理论进行了局部轨迹规划,确保了轨迹的安全性。在Matlab/Simulink环境下对本文方法进行了仿真验证。仿真结果表明该方法能够有效地实现预期的轨迹规划功能。

(2)相比于传统方法,本文方法在保证动态规划换道过程的全局最优性的基础上进行了补充。

(3)本文中没有讨论中观行车行为的动态规划方法,未来针对该领域的研究可围绕此内容展开。