车辆换挡离合器在接合过程中,伴随着大量机械能转化为内能,较高的温升引起摩擦副材料受热变形较大,这就导致了摩擦元件经常工作在高温、高压的恶劣环境中,容易出现摩擦因数热衰退、表面高温烧蚀、震动噪声等问题。这些问题将导致车辆传动系统整体性能下降甚至失效。

国外学者对于离合器温度场的非均匀分布问题研究主要以由Barber^{[ 1]}提出的热弹性不稳定(TEI)理论为基础。研究发现^{[ 2, 3]},在摩擦副滑摩过程中,非均匀接触压力会导致非均匀摩擦热,进而导致非均匀的温度场,随之产生的非均匀热弹性变形会进一步影响接触压力的分布。这个过程循环往复,当摩擦副相对速度超过临界速度时,各种扰动均随时间呈指数增长,最终形成局部高温区(热点),此时系统处于热弹性不稳定状态。

Du等^{[ 4]}采用有限元方法计算由热导体和热绝缘体组成的摩擦系统的热弹性模型,将求解系统热弹性不稳定临界速度问题转化为求解系统矩阵特征值问题。Yi等^{[ 5]}利用有限元法建立了由有限厚度热导体组成的离合器接合过程的三维模型,采用特征值方法求解了扰动增长系数,利用扰动增长系数计算系统临界速度;Ahn等^{[ 6]}通过建立瞬态二维有限元模型分析摩擦副的热弹塑性不稳定性,发现在摩擦副相对速度低于临界速度时,其塑性变形与初始扰动幅值无关,初始扰动幅值仅影响出现非均匀接触的间隔时间。

本文建立了离合器接合过程的三维有限元模型,求解离合器在不同转速下的扰动增长系数,并根据扰动增长系数计算系统发生TEI时的临界速度。通过计算和分析离合器结构参数与临界速度的关系,得到改善离合器热弹性稳定性的途径,为离合器结构优化设计提供参考和依据。

Lee等^{[ 2]}与Decuzzi等^{[ 3]}通过建立二维理论模型分析摩擦元件的热弹性不稳定性问题,得到了系统发生TEI的临界速度。因为由TEI引起的热点主要沿离合器圆周方向分布,所以二维模型中不考虑离合器半径方向,只考虑圆周方向和厚度方向,得到了较准确的临界速度。

利用二维模型,无法研究离合器半径尺寸、内外径比等结构参数对TEI的影响,所以,本文将建立离合器接合过程三维有限元模型,通过编程求解不同滑摩速度下的扰动增长系数,通过分析扰动增长系数的变化规律,求解系统发生TEI时的临界速度,并研究不同结构参数对临界速度的影响。

选取一对由摩擦片与对偶片构成的摩擦副建立三维模型,其中材料1代表摩擦片,材料2代表对偶片,摩擦片、对偶片分别以速度ω₁、ω₂旋转运动,如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 离合器有限元模型原理图Fig.1 Schematic diagram of clutch’s finite element model

由于离合器摩擦片和对偶片存在表面粗糙度、安装误差、加载系统不稳定性等原因,摩擦副接触压力在圆周方向上存在扰动。接触压力可以分解为稳态压力和扰动压力,假设扰动压力为余弦形式,幅值随时间呈指数变化^{[ 1]}的表达式为:

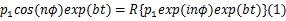
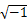
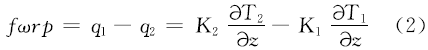
式中: n表示盘片表面热点数; ϕ表示角坐标; b表示扰动增长系数;R表示复数取实部,i = 。接触压力扰动会引起摩擦热的非均匀性,进而影响温度场分布。摩擦副处的能量平衡方程为:

式中: f、 ω、 r、 p、 q、 K、 T、 z分别表示摩擦因数、角速度、离合器半径、接触压力、热流密度、导热系数、温度和 z-柱坐标的 z方向。

根据方程(2),材料温度场存在如下余弦扰动:

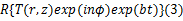
摩擦片与对偶片温度场均符合柱坐标系下的固体瞬态热传导方程:

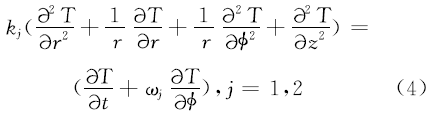
式中: k表示材料热扩散系数:

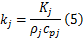
式中: ρ、 c_p分别表示材料密度和比热。

将温度场扰动表达式(3)代入热传导方程(4)得:

（6）

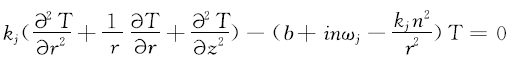
采用伽辽金法将瞬态热传导偏微分方程问题转化为线性方程组问题,温度场扰动幅值转化为:

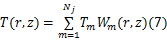
式中: N、 T_m、 W_m分别表示节点数、节点温度和形函数。

根据伽辽金法中权函数与形函数相同,将温度扰动幅值方程(7)代入热传导方程(6)并积分可得:

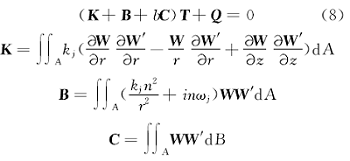
式中: A表示摩擦副接触面积; W'表示形函数矩阵的转置,即权函数。热流密度矩阵 Q为:

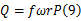
式中: P表示接触压力矩阵。假设 P与温度矩阵 T的关系为:

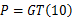
转换矩阵 G可以通过两种方法求解。方法1是利用Abaqus、Ansys等大型有限元软件,仿真模拟离合器滑摩过程,求解节点接触压力与温度,从而得到矩阵 G;方法2是通过编写有限元计算程序,求解矩阵 G。方法2的优点是计算效率高,计算过程可控。本文采用方法2,有限元程序由丹佛大学的Yi Y B教授^{[ 5]}编写。将方程(9)(10)代入方程(8)可得:

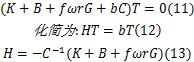
通过求解矩阵 H的特征值与特征向量,即可得到不同角速度下的扰动增长系数 b与温度场扰动矩阵 T,当扰动增长系数为零时,对应的转速 ω即为临界速度。

研究对象选取车辆换挡离合器,对偶片材料选取65^#Mn钢,摩擦材料分别选取铜基粉末冶金材料与纸基摩擦材料,如表1所示。结构参数选取某液力机械综合传动装置中的换挡离合器,对偶片(摩擦片)内、外径分别为86 mm、125 mm;摩擦片、对偶片的半厚度分别为0.6 mm、2 mm。摩擦因数取0.13。

表1

Table 2

表1(Table 2)

表1 换挡离合器材料参数 Table 2 Material properties of shift clutch 参数 铜基粉末材料 65#Mn钢 弹性模量 E/GPa 2.26 160 泊松比ν 0.29 0.29 热膨胀系数α/10-5K-1 1.21 1.27 导热系数 K/(W·m·K-1) 9.3 45.9 密度 ρ/(kg·m-3) 5500 7800 比热容 cp/(J·kg-1·K-1) 460 487

表1 换挡离合器材料参数 Table 2 Material properties of shift clutch

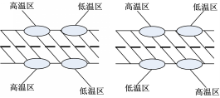
根据Lee的研究,摩擦系统发生TEI时,摩擦片发生对称热弹性变形,对偶片发生反对称热弹性变形^{[ 2]},不同变形模式的高温区与低温区如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 热弹性变形高温区分布图(a) 对称变形 (b) 反对称变形Fig.2 Distribution map of thermoelastic hot spots

对称变形下材料中线处的边界条件为:

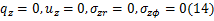
反对称变形下材料中线处的边界条件为:

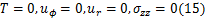
式中: u、 σ分别表示材料的热弹性变形与热弹性应力。

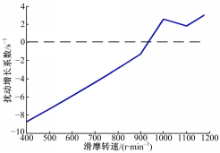
根据表2、表3,以及边界条件(11)(12),计算铜基材料离合器在不同滑摩转速下的扰动增长系数如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 扰动系数变化图Fig.3 Variation diagram of growth rate

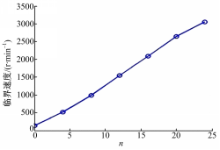
由图3可知,随着滑摩转速的增大,扰动增长系数基本呈上升趋势,当扰动系数为零时,对应的滑摩转速即为临界速度,当热点数 n=8时,临界速度为920 r/min。通过类似方法,可以求解不同热点数下的系统临界速度。计算铜基材料离合器的TEI临界速度,如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 离合器临界速度曲线图Fig.4 Critical speed of clutches

由图4可知,不同热点数 n对应不同临界速度,热点数 n与系统内扰动空间频率 m的关系为:

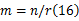
所以,不同空间频率的扰动对应的临界速度不同。临界速度曲线下方表示稳定区域,上方表示热弹性不稳定区域。当离合器滑摩速度超过临界速度时,只有在一定频率的扰动激励下,摩擦副表面才会出现热点。例如,采用铜基材料的离合器接合速度为1000 r/min,如果滑摩时间足够长,盘片可能出现0~7个热点。

同时,系统临界速度曲线上的最低点是判断热弹性稳定性的主要标准。离合器最小临界速度越小,离合器稳定性越差,更容易在接合过程中出现局部高温而失效。所以,在离合器设计中,应当优化设计离合器结构参数,提高离合器临界速度,特别是最小临界速度。可优化的结构参数包括半径参数(内径、外径、内外径比),厚度参数(摩擦片厚度、对偶片厚度、摩擦片与对偶片厚度比)等。

2.1 离合器半径

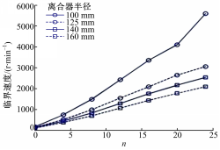
离合器摩擦片和对偶片半径是影响其热弹性稳定性的重要因素,改变半径尺寸会引起功率密度以及滑摩线速度的改变。首先,保持离合器内外径比0.688不变,外径分别取100、125、140、160 mm,对应内径分别为68.8、86、96、110 mm,临界速度变化曲线如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 离合器半径对临界速度的影响Fig.5 Effect of clutches radius on critical speed

根据图5,离合器半径增大引起临界速度降低,说明系统热弹性稳定性下降。原因是在相同角速度条件下,离合器半径增大,引起摩擦副的相对运动线速度增大,从而导致离合器稳定性下降。

离合器内外径之比会影响离合器传递功率与转矩的能力,也是影响系统稳定性的重要因素。保持离合器外径125 mm不变,内外径比分别取0.4、0.5、0.688、0.8,对应内径分别取50、62.5、86、100 mm,绘制内外径比与临界速度的关系曲线如图6(a)所示。

根据图6(a)可知,当离合器内外径比值较小时,随着内外径比值的减小,临界速度明显增大;当内外径比值较大时,临界速度随内外径比变化而产生的变化较小。当内外径比由0.688增大到0.8时,在热点数小于17时,临界速度减小,热点数大于17时,临界速度增大,二者对应的临界速度差值较小。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 离合器内外径比对临界速度的影响Fig.6 Effect of ratio of inner radius to outer radius on critical speed

产生这种现象的原因有两方面:①在离合器外径尺寸不变的条件下,离合器内外径比值减小,摩擦副接触面积增大,功率密度减小,降低了接合过程的稳态温升和温度扰动,有利于提高离合器热弹性稳定性;②离合器内外径比值减小,会造成内外径滑摩线速度差值增大,内外半径处的摩擦热流密度差别增大,从而导致离合器温度场在半径方向上的非均匀性增大,离合器热弹性稳定性降低。

根据图6(b)可知,当离合器内外径比值小于0.6时,功率密度对稳定性的影响占主导地位,即减小内外径比,临界速度增大,稳定性提高。当内外径比值大于0.6时,功率密度因素与内外径线速度因素对稳定性的影响基本相互抵消,即临界速度基本不随内外径比值变化。

传统离合器设计中,考虑使用原因和制造工艺以及经济性,一般摩擦片内外径比值不能小于0.7。过大的摩擦片宽度会引起离合器在使用过程中出现烧结以及蝶形变形和扭曲^{[ 7]}。所以,在离合器设计中,适当增大内外径比值,既可以保证热弹性稳定性,又可以降低成本,减少离合器盘片烧结和扭曲变形。

2.2 离合器对偶片与摩擦片厚度

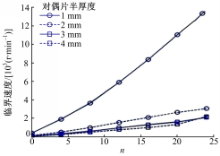
离合器对偶片与摩擦片厚度会影响其热容量,从而影响离合器接合过程的温度场分布和热弹性稳定性。首先,保持其他结构参数和材料参数不变,对偶钢片半厚度分别取1、2、3、4 mm,绘制临界速度与对偶片厚度关系的完整曲线,如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 对偶片厚度对临界速度的影响Fig.7 Effect of thickness of mating disk on critical speed

由图7可知,当离合器对偶片半厚度小于2 mm时,随着其厚度的减小,临界速度明显增大。当对偶片半厚度大于2 mm时,临界速度基本不随对偶片厚度的变化而改变。引起这种现象的因素有3方面:

(1)在硬度不变的条件下,对偶片厚度减小,在相同温度场和接触压力作用下,对偶片更容易发生热弹性变形,有助于减小对偶片内部应力,从而提高稳定性。

(2)对偶片厚度减小,在降低内部热弹性应力的同时,会引起摩擦热和温度场的非均匀性增大,降低系统的稳定性。

(3)在离合器半径尺寸不变的前提下,离合器对偶片厚度增加,其体积增大,系统热容量相应增大。在相同摩擦热作用下,对偶片温度降低,温度场的非均匀性也相应降低,系统热弹性稳定性提高。

根据图7,当对偶片半厚度小于2 mm时,因素(1)起主导作用,即减小对偶片厚度提高系统稳定性。当对偶片半厚度大于2 mm时,因素(1)与因素(2)(3)基本相互抵消,即临界速度基本不随对偶片厚度变化。离合器设计中,应当在保证对偶片具有一定热容量的前提下,尽量减小其厚度,以提高系统热弹性稳定性。

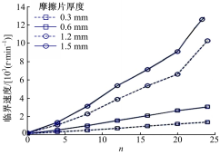
保持其他参数不变,钢片半厚度选取2 mm,摩擦片半厚度分别取0.3、0.6、1.2、1.5 mm,摩擦片厚度与临界速度关系如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 摩擦片厚度对临界速度的影响Fig.8 Effect of thickness of frictional disk on critical speed

根据图8可知,临界速度随离合器摩擦片厚度的增大而增大,其原因是当摩擦片厚度增大时,摩擦片与对偶片厚度比增大,同时对偶片热容量不变,所以由于因素(1)的影响,系统热弹性稳定性提高。同时,由于摩擦片导热性相对较差,仅有少量摩擦热传导进入摩擦片,所以因素(2)(3)的影响在摩擦片中基本可以忽略。为验证此分析,可在保持对偶片厚度不变的条件下,计算不同厚度比时的临界速度,如图9所示。

图9中,临界速度随摩擦片与对偶片厚度比的增大而增大,反应的趋势与图8一致,说明离合器设计中,在制造工艺和成本允许的前提下,应当增大摩擦片与对偶片厚度比,以提高系统热弹性稳定性。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 摩擦片与对偶片厚度比对临界速度的影响Fig.9 Effect of thickness ratio of frictional disk to mating disk on critical speed

(1)离合器接合过程中,不同转速对应不同扰动增长系数。当扰动增长系数为正时,系统进入热弹性不稳定状态,温度场和接触压力扰动随时间的延长呈指数增长。扰动系数恰好等于零时,

对应的滑摩速度为临界速度。

(2)不同频率扰动对应不同临界速度,临界速度曲线的最小值是衡量系统热弹性稳定性的重要指标。

(3)减小离合器半径尺寸,有利于提高离合器热弹性稳定性。

(4)离合器内外径比值小于0.6时,减小内外径比值有利于提高临界速度和稳定性;内外径比值大于0.6时,临界速度与内外径比值基本无关。

(5)离合器对偶片半厚度小于2 mm时,减小对偶片厚度有利于提高临界速度和稳定性;对偶片半厚度大于2 mm时,临界速度基本与对偶片厚度无关。

(6) 增大离合器摩擦片厚度,有利于提高临界速度和系统稳定性。