引用本文
方志刚, 过学迅, 左磊, 徐琳, 张晗. 液电馈能式减振器阻尼特性理论及试验. 2014, 44(4): 939-945
[FANG Zhi-gang, GUO Xue-xun, ZUO Lei, XU Lin, ZHANG Han. Theory and experiment of damping characteristics of hydraulic electromagnetic energy-regenerative shock absorber. Journal of Jilin University Engineering and Technology Edition, 2014, 44(4): 939-945]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
液电馈能式减振器阻尼特性理论及试验
方志刚1, 过学迅1, 左磊2, 徐琳1, 张晗1
1.武汉理工大学 现代汽车零部件技术湖北省重点实验室,武汉 430070
2.纽约州立大学石溪分校 机械工程系,石溪 11794
通信作者：过学迅（1956-）,男,教授.研究方向:汽车传动系统理论与汽车节能技术.E-mail:guo6531@163.com

作者简介：方志刚（1984-）,男,讲师,博士.研究方向:汽车动力学与汽车节能技术.E-mail:zuoleng136@163.com

基金:国家自然科学基金项目（51075312）; 中央高校基本科研业务费专项项目（2014-Ⅳ-036）;
摘要

提出了液电馈能式减振器(HESA)的简化模型,从液压整流桥、液压马达以及管路的损失等方面分析了液压回路的压降,推导了HESA的理论阻尼力;试制了HESA的样机并建立了相应的试验台架,对HESA的样机进行了台架试验,对比分析了试验数据以及理论数据。结果表明,在激励频率为1.67 Hz、激励幅值为12.5 mm时,HESA的理论阻尼力与试验阻尼力吻合很好,具有很高的准确性,随着激励幅值的增大,试验阻尼力与理论阻尼力的偏差增大;相比伸张行程,压缩行程的试验阻尼力与理论阻尼力吻合得更好。

关键词: 车辆工程; 馈能减振器; 振动分析; 阻尼特性
中图分类号:U461.4 文献标志码:A 文章编号:1671-5497(2014)04-0939-07
Theory and experiment of damping characteristics of hydraulic electromagnetic energy-regenerative shock absorber
FANG Zhi-gang1, GUO Xue-xun1, ZUO Lei2, XU Lin1, ZHANG Han1
1.Hubei Key Laboratory of Advanced Technology of Automotive Parts, Wuhan University of Technology, Wuhan 430070, China
2.Department of Mechanical Engineering, State University of New York at Stony Brook, Stony Brook 11794, USA
Abstract

A simplified model of Hydraulic Electromagnetic energy-regenerative Shock Absorber (HESA) was proposed. The pressure drop of the hydraulic circuit was analyzed from the loss in the hydraulic rectifier, the hydraulic motor and pipeline. The theoretical damping force of HESA was deduced. A HESA prototype was manufactured, the corresponding test bench was built. The experiment of the prototype was carried out, and the experimental data was compared with the theoretical data. Results indicate that, under the condition of excitation frequency of 1.67 Hz and excitation amplitude of 12.5 mm, the experimental damping force of HESA is in good agreement with the theoretical value. The deviation of the experimental data from the theoretical value increases with the amplitude. The deviation of the experimental data from the theoretical value in the compression stroke is smaller than that in the extension stroke.

Keyword: vehicle engineering; regenerative shock absorber; vibration analysis; damping characteristic
0 引 言

汽车的能量回收主要有发动机热能回收、制动能量回收以及减振器能量回收。馈能式减振器的主要类型有直线电机式[ 1, 2]、滚珠丝杠式[ 3, 4, 5]、齿轮齿条式[ 6, 7]以及液压传动式[ 8, 9, 10],本文的研究对象为液压传动式,即液电馈能式减振器。国内外许多学者对馈能式减振器的馈能特性进行了大量研究,Wendel等[ 11]提出通过能量回收马达来回收部分能量,从而最小化悬架主动控制所需能量,并且分析了可行的液压马达的方案和对应方案的控制策略。Okada等[ 12]提出了利用一个电机作动器在减振器高速运动时回收振动能量。在低速运动,运用主动控制算法来控制电机作动器以提供良好的阻尼性能。通过仿真与简易试验证明了这套系统的性能在优于被动悬架系统的同时还可回收能量。

能量回收固然重要,但若在能量回收过程中引起减振器的减振性能降低,不仅会降低乘坐舒适性,还可能会影响车辆的操纵稳定性,进而导致车辆安全性的下降,因此馈能式减振器设计的第一要素为减振。许多学者也对馈能式减振器的减振特性进行了研究,Suda等[ 13]对馈能式减振器进行了深入的研究,从理论上分析了减振性能与能量回收的平衡,完善了馈能减振器的主动控制策略,仿真结果表明:当车辆以80 km/h的速度行驶在C级路面上时,若系统激励频率小于2 Hz,系统耗散能量,若激励频率大于2 Hz,系统回收能量。Tang等[ 2]从理论上分析了齿轮齿条式馈能减振器的阻尼特性,重点考虑齿隙与摩擦的影响,并通过台架试验验证了阻尼力模型的正确性。本文的研究重点为在理论推导HESA的阻尼力理论模型的同时,结合台架试验,验证模型的正确性,并充分运用试验数据分析HESA的固有特性。

1 简化的HESA模型

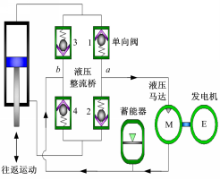
HESA的原理在文献[8-10]中已经进行了叙述,简化的HESA模型去掉了液压马达前端蓄能器,其原理图如图1所示。将液压缸安装在原减振器的位置,当液压缸受到外部激励时,其高压腔内的高压油受挤压而流入液压整流桥。经液压整流桥整流后,高压油液从其出口 a流出,进而驱动液压马达,液压马达带动发电机进行发电。而从液压马达流出的油液则继续向前流动,经蓄能器稳压后从液压整流桥的入口 b流回液压整流桥,最后到达液压缸的低压腔,这样就完成了一次油液的循环,同时也完成了能量的回收。

图1 简化的HESA原理图Fig.1 Schematic diagram of simplified HESA

对比HESA的模型,简化的HESA模型去掉了液压整流桥出口 a处与液压马达之间的蓄能器,该蓄能器的作用主要是用于稳定液压马达的转速,提高发电机的工作效率。然而蓄能器在储能的同时亦会消耗能量[ 14],且该蓄能器的开启压力、容积以及刚度的设计不仅受路面激励、车辆类型的影响,还受其与马达后端蓄能器共同克服液压缸容积变化的影响。因此,为简化模型以及便于理论设计计算,去掉了马达前端蓄能器。

2 模型阻尼特性的理论分析
2.1 普通减振器

图2 减振器自由体受力图Fig.2 Free body diagram of shock absorber

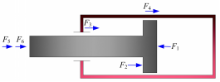
普通减振器无论是单筒式还是双筒式,其自由体受力图如图2所示。图中 F1为压缩腔油液作用在活塞底部上的压力; F2为复原腔油液作用在活塞杆一侧活塞环面上的压力; F3为活塞杆油封作用在活塞杆上的摩擦力,它的方向始终与相对运动方向相反; F4为活塞与缸筒上的机械摩擦力,它的方向也始终与相对运动的方向相反; F5为外部连接件作用在活塞杆上的机械压缩力; F6为大气压作用在活塞杆截面上的压力,当油液系统压力用表压表示时, F6 =0。

减振器的阻尼力为:

∑ F=F2 +F3 +F4 +F5 +F6 -F1

2.2 简化的HESA

简化的HESA的原理图如图1所示,作为一种新型减振器,其阻尼力的特性以及组成均与普通的双筒作用减振器不同,因此有必要对液电馈能式减振器的阻尼力进行推导与分析。在进行分析之前需要进行适当的简化与假设,文中忽略了油液在管路中由于管路局部扩张或收缩而形成的局部损失以及与图2中的 F3与 F4处形成的类似机械摩擦力,主要考虑液压回路中由于压降而形成的阻尼力,即液压整流桥的压降、液压管路的沿程压力损失以及液压马达的压降。

现假设HESA方案中液压缸活塞的直径为 D,活塞杆的直径为 Dr。则可得液压缸中活塞的面积 A与活塞杆的面积 Ar分别为:

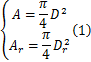
所以,复原腔一侧活塞环面面积 Aa为:

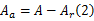
由于活塞杆的存在,当活塞作等振幅运动时,减振器压缩行程与伸张行程排出的高压油流量不等。现假定减振器受到正弦位移激励,激励的频率为 f,振幅为 l,则减振器的位移为:

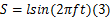
对应地,减振器的速度为:

在压缩行程时,系统的阻尼力可表示为:

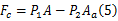
式中: P1为压缩腔内的压强; P2为伸张腔内的压强。

此时,压缩腔为高压腔,不考虑油液的局部损失以及液压缸的内泄漏,则系统的油液存在如下压力平衡方程:

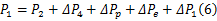
式中: ΔPp为管路的沿程压力损失; ΔPe为液压马达的压降; ΔPi为第 i个单向阀的压降, i=1、2、3、4。

由于HESA方案中液压缸两腔分别为有杆腔与无杆腔,因此液压缸存在容积变化的现象。双筒减振器为降低其系统容积变化的不利影响,常在其气腔中充入压力为(4~6)×105 Pa的氮气,起到在平衡系统容积变化的同时使低压腔及时回油的作用。在HESA中,可以通过外接液压泵站的方式,使液压缸活塞在其平衡位置附近时,液压回路中的油液压力 Po约为5×105 Pa。HESA与双筒减振器类似,在受到高频激励时系统可能出现空程畸变的现象。因为低压腔的回油不及时,导致低压腔的压力迅速降低至油液的蒸发压力,油液蒸发形成空穴而产生空程畸变现象[ 15]。为防止空程畸变现象的发生,要求蓄能器能有效稳定系统的回油压力,并使回油管路的表压不低于0 Pa。所以蓄能器的开启压力应设计为尽可能小,当回油管路油液压力低于一个大气压时,蓄能器不再具有稳压的作用。设计时还要求单向阀3和4的阻抗尽可能地小,以减小低压腔压力的进一步降低。

假设蓄能器与减振器低压腔之间的管路较短,其沿程压力损失可忽略(在实际的HESA的样机中,蓄能器集成在液压缸上方,其最长管路也仅为液压缸上腔至下腔的长度),则蓄能器的压力为:

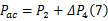
将式(6)(7)代入式(5)中可得:

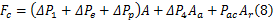
从式(8)中可以看出,对于简化的HESA,其压缩行程的阻尼力由三项组成:液压整流桥中单向阀1的压降、液压马达的压降以及管路压力损失作用在活塞端面上的力;单向阀4的压降作用在活塞环面上的力;蓄能器压力作用在活塞杆截面积的力。

2.2.1 压力

从式(8)中还可发现,在简化的HESA方案中,若液压缸确定,即液压缸活塞端面直径、活塞杆径确定后,HESA的阻尼力仅与液压回路各组成部件的压降以及蓄能器的压力相关,因此若确定回路中各处的压降以及蓄能器的压力,便可推导出简化的HESA的理论阻尼力。

(1)单向阀的压降

单向阀工作时的压降常采用薄壁小孔公式来计算[ 16]:

式中: Qi为第 i个单向阀的流量; Aci为第 i个单向阀的开口面积; cq为油液的流量系数,计算时设为定值0.6; ρ为油液的密度。

单向阀的压降为:

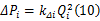
式中: kΔi为单向阀的阻抗, kΔi= 。

(2)液压马达的压降

高压油液驱动液压马达时,马达的转速与输出力矩满足:

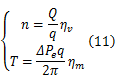
式中: q为液压马达的排量; ηv为液压马达的容积效率; ΔPe为液压马达出入口油液的压差; ηm为液压马达的机械效率。

马达驱动发电机,则可得到发电机的电压与力矩满足:

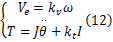
式中: Ve为感应电动势, Ve =IR,其中 R为电路中的总电阻; kv为反电动势常数; ω为发电机转子的转速, ω=2 πn; J为发电机转子的惯量; 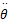为发电机转子的角加速度; kt为发电机的力矩常数; I为电流。

感应电动势与文献[17]类似,忽略转子的转动惯量,则综合式(11)与(12)可得:

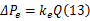
式中: ke为液压马达的阻抗, ke = 。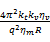

(3)管路的压降

在此小节中,管路的压降指的是管路的沿程损失,暂不考虑其局部损失。根据达西公式[ 16],管路的沿程损失水头不仅与管段的长度成正比,还与管道的直径成反比。所以管路的沿程损失水头为:

式中: λ为沿程损失系数; L为管路的长度; vc为管路中油液的流速; g为重力加速度; d为管路的直径。

沿程损失系数与雷诺数存在如下关系:

式中: υv为油液的运动黏度。

最终可得沿程压力损失方程:

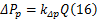
式中: kΔp为管路沿程压降, kΔp = 。

(4)蓄能器的压力

弹簧蓄能器的刚度与尺寸很难满足HESA液压回路中系统压力变化的要求,因此选取气囊式蓄能器。而气囊内气体压力与体积存在如下关系:

Po 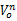=Pac

式中: Po为液压回路的保压压力; Vo为气囊在其气体压力为 Po时的容积; Vac为蓄能器吸收油液的体积; n为绝热指数。

蓄能器的容积变化实际上是时间的函数,它与液压缸的容积变化存在如下关系:

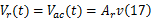
根据液压缸的容积变化特性,当活塞运动至压缩腔一侧时,蓄能器相对其平衡位置的状态一定,为油液吸收状态。为保证蓄能器的工作可靠性要求,其吸收的油液量小于 Vo。当活塞运动至复原腔一侧时,蓄能器相对其平衡位置的状态一定,为油液释放状态,为保证蓄能器能有效稳定回油管路油液压力,要求其释放的油液量应不大于其初始的储油量。所以蓄能器的设计存在如下约束条件:

式中: VT为蓄能器的额定容积。

综合可得蓄能器的压力满足:

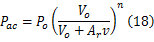
从式(18)可以看出,蓄能器的压力(即液电馈能式减振器中低压腔的回油压力)由系统的保压压力、气囊在保压压力下的容积、活塞杆截面积以及减振器速度决定。

2.2.2 流量

在液压系统中,油液的压力与流量密不可分,因此有必要对HESA液压回路中各部件的流量进行分析。当减振器处于压缩行程时,若不考虑油液的可压缩性以及微小的内、外泄漏,液压整流桥中单向阀1与液压马达的流量为:

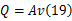
油液从马达流出后,经过蓄能器,蓄能器吸收部分油液稳压,然后油液继续向前流动,流向液压整流桥中的单向阀4,则单向阀4的流量为:

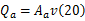
2.2.3 阻尼力

综合以上分析可得,在压缩行程时液电馈能式减振器的阻尼力为:

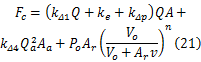
同理,可得伸张行程时HESA的阻尼力为:

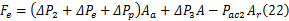
综合可得液电馈能式减振器的阻尼力为:

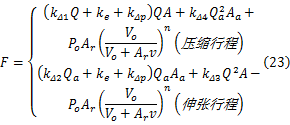
对应的阻尼系数为:

3 模型阻尼特性台架试验

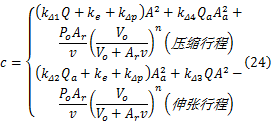
按照HESA的原理图试制了相应的原理样机,并建立了相应的试验台架,如图3所示。其中减振器的样机集成了液压缸、液压整流桥以及蓄能器,而液压马达、发电机以及各连接管路等则布置在台架的面板上。试验按照标准QC/T545-1999汽车筒式减振器台架试验方法进行[ 18]。在标准QC/T545-1999中,要求减振器的台架试验有示功特性试验、速度特性试验、温度特性试验以及耐久性试验。在本小节中主要进行的试验仅有示功特性试验,HESA研究的现阶段为样机的原理验证、性能验证与探索阶段,速度特性试验主要用于悬架匹配,温度特性试验与耐久性试验用于验证产品的鲁棒性。因此,暂不对HESA的速度特性试验、温度特性试验以及耐久性试验进行研究。

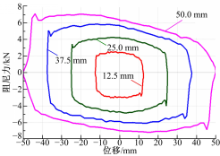
图3 简化的HESA试验台架Fig.3 Test bench of simplified HESA

在试验台架中,各组成零部件的参数如表1所示。其中发电机连接电子负载,且控制负载电路为稳流电路,台架试验的激励为正弦位移激励,激励频率为 f,激励的幅值 l分别选取为12.5、25、37.5和50 mm,得到简化的HESA的试验示功图如图4所示。

表1 HESA参数 Table 1 Parameters of HESA

图4 简化的HESA示功图Fig.4 Indicator diagram of simplified HESA

在图4中,阻尼力为正时表示拉伸力,阻尼力为负时为压缩力。从图4可以看出,简化的HESA现阶段样机存在如下特性:

(1)在阻尼力每次变换方向即阻尼力由正变为负或由负变为正时均存在力的突变,其原因为HESA的样机与试验台架存在安装间隙,该现象在最终装车时是可以消除的。

(2)HESA的样机在压缩行程的阻尼力相比伸张行程要大,但相差甚微,而要实现传统减振器要求的伸张行程阻尼力大于压缩行程的阻尼力,可以通过式(23)对HESA的相关参数进行有针对性的设计,从而增大伸张行程阻尼力或减小压缩行程的阻尼力,使其尽可能达到与双筒减振器类似的阻尼特性。

(3)在1.67 Hz的激励下,当激励的幅值不大于25 mm时,HESA的示功图非常饱满亦非常理想,但随着激励幅值的增大,如达到50 mm时,HESA的示功图发生了形变,阻尼力的极值不在 Y轴上,而是出现在第二与第四象限,出现该现象的原因可能为,随着激励幅值的增大,试验台架自身发生同频率的沿龙门方向的摆振,而激励源输入的位移激励始终与重力方向保持一致,这使得减振器活塞与缸筒的摩擦阻力增大,从而影响了HESA的示功特性。

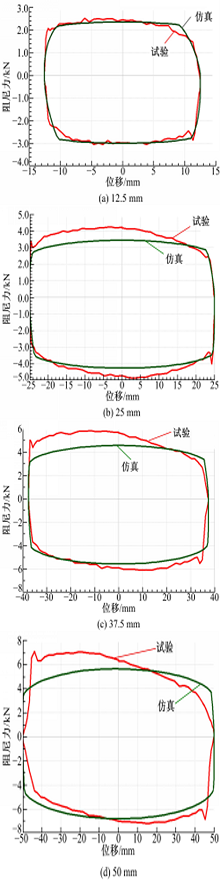
根据式(23)以及表1中的参数,可通过理论计算得到HESA的理论阻尼力,对比试验数据与理论计算的结果如图5所示。

图5 理论示功特性与试验示功特性对比Fig.5 Comparison between theoretical data and experimental data

从图5中可以看出,在激励频率为1.67 Hz时,可以得到如下结论:

(1)在激励幅值较小(如12.5 mm)时,HESA的理论计算结果与试验数据吻合很好。

(2)无论激励的幅值如何变化,压缩行程阻尼力的理论值与试验值吻合比伸张行程要好。

(3)随着激励幅值的增大,伸张行程阻尼力的理论值与试验值偏差增大。

另外在相同激励频率下,随着激励幅值的增大,减振器的最大速度也相应的增大,这也增大了油液在传递过程中的局部损失,而在理论计算时未考虑局部损失的影响。

4 结束语

提出了简化的液电馈能式减振器模型,对其阻尼力的组成(包括液压整流桥、马达与管路的压降以及蓄能器的压力)进行了理论计算,通过样机的台架试验得出了样机的阻尼特性,并对比分析了理论数据与试验数据,得出在1.67 Hz激励频率、12.5 mm位移激励下理论数据与试验数据吻合很好;随着激励幅值的增大,理论数据与试验数据的偏差增大;相比伸张行程,压缩行程时理论数据与试验数据吻合得较好。造成理论数据与试验数据存在偏差的主要原因为油液的局部损失随着激励幅值的增大而增大,且当激励幅值较大时,台架自身的摆振也增大了其偏差。液电馈能式减振器理论模型的建立,不仅可以用于指导其性能参数的匹配设计,还可以为能量回收提供参考依据。采用性能更好的台架、适当考虑油液的局部损失,并增加其他激励频率以及激励幅值的试验来验证理论模型,将使理论模型更具说服力。

The authors have declared that no competing interests exist.

参考文献
[1] Jones W, Bose Corp. Uses speaker technology to give cars adaptive suspension[J]. IEEE Spectrum, 2005, 42(5): 12-14. [本文引用:1] [JCR: 1.322]
[2] Tang Xiu-dong, Zuo Lei. Towards MESO and Macro scale energy harvesting of vibration[C]∥Proceedings of the ASME 2009 International Mechanical Engineering Congress & Exposition, Florida, USA, 2009: 885-896. [本文引用:2]
[3] Nakano K, Suda Y. Combined type self-powered active vibration control of truck cabins[J]. Vehicle System Dynamics, 2004, 41(6): 449-473. [本文引用:1] [JCR: 0.766]
[4] 曹民, 刘为, 喻凡. 车辆主动悬架用电机作动器的研制[J]. 机械工程学报, 2008, 44(11): 224-228.
Cao Min, Liu Wei, Yu Fan. Development on electromotor actuator for active suspension of vehicle[J]. Chinese Journal of Mechanical Engineering, 2008, 44(11): 224-228. [本文引用:1] [CJCR: 1.505]
[5] 王庆年, 刘松山, 王伟华, 等. 滚珠丝杠式馈能型减振器的结构设计及参数匹配[J]. 吉林大学学报: 工学版, 2012, 42(5): 1100-1106.
Wang Qing-nian, Liu Song-shan, Wang Wei-hua, et al. Structure design and parameter matching of ball-screw regenerative damper[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(5): 1100-1106. [本文引用:1] [CJCR: 0.701]
[6] Li Zhong-jie, Brindak Zachary, Zuo Lei. Modeling of an electromagnetic vibration energy harvester with motion magnification[C]∥Proceedings of the ASME 2011 International Mechanical Engineering Congress & Exposition, Denver, USA, 2011: 285-293. [本文引用:1]
[7] 于长淼, 王伟华, 王庆年. 馈能悬架阻尼特性及其影响因素[J]. 吉林大学学报: 工学版, 2010, 40(6): 1482-1486.
Yu Chang-miao, Wang Wei-hua, Wang Qing-nian. Damping characteristic and its influence factors in energy regenerative suspension[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(6): 1482-1486. [本文引用:1] [CJCR: 0.701]
[8] Xu Lin. Structure designs and evaluation of performance simulation of hydraulic transmission electromagnetic energy-regenerative active suspension[C]∥SAE Paper, 2011-01-0760. [本文引用:1]
[9] Xu Lin. Controlling methods study on damping force of hydraulic electromagnetic energy-regenerative absorber[C]∥SAE Paper, 2011-01-0761. [本文引用:1]
[10] Fang Zhi-gang, Guo Xue-xun, Xu Lin. Energy dissipation and recovery of vehicle shock absorbers[C]∥SAE Paper, 2012-01-2037. [本文引用:1]
[11] Wendel G R, Stecklein G L. A regenerative active suspension system[C]∥SAE Paper, 910659. [本文引用:1]
[12] Okada Y, Harada H, Suzuki K. Active and regenerative control of an electro dynamic-type suspension[J]. Japan Society of Mechanical Engineers, 1997, 40(2): 272-278. [本文引用:1]
[13] Kawamoto Y, Suda Y, Inoue H, et al. Modeling of electromagnetic damper for automobile suspension[J]. Journal of System Design and Dynamics, 2007, 1(3): 524-536. [本文引用:1]
[14] 权凌霄, 孔祥东, 高英杰, 等. 不考虑进口特性的蓄能器吸收冲击理论及试验[J]. 机械工程学报, 2007, 43(9): 28-32.
Quan Ling-xiao, Kong Xiang-dong, Gao Ying-jie, et al. Theory and experiment of accumulator absorbing pressure pulsation without regard to its entrance characteristics[J]. Chinese Journal of Mechanical Engineering, 2007, 43(9): 28-32. [本文引用:1] [CJCR: 1.505]
[15] 俞德孚, 李晓雷, 马彪. 车辆悬架减振器的理论和实践[M]. 北京: 兵器工业出版社, 1988. [本文引用:1]
[16] 赵汉中. 工程流体力学[M]. 武汉: 华中科技大学出版社, 2011. [本文引用:2]
[17] Stephen N G. On energy harvesting from ambient vibration[J]. Journal of Sound and Vibration, 2006, 293(1-2): 409-425. [本文引用:1] [JCR: 1.613]
[18] QC/T545-1999. 汽车筒式减振器台架试验方法[S]. 1999. [本文引用:1]