作者简介:徐洪峰(1978-),男,副教授,博士.研究方向:中微观交通组织,管理与控制. E-mail:xu_hong_feng@126.com
面向四路环形交叉口,以安全、高效地实施单进口轮流放行方式的交通信号控制为基本目的,采用非优化建模的思想,建立了具有4个进口道机动车相位、4个环道机动车相位和4个行人相位的相位结构设计方法,提取了4项通行权供给的时间特性,建立了有条件地满足所有道路使用者的通行时间资源需求的信号配时设计方法。仿真实验结果表明,本文方法能够在机动车交通高峰时段有效遏制环形交叉口整体性能的显著恶化,分时段实施让行规则控制和交通信号控制是十分必要的。
Regarding fully signalized four-leg roundabouts, a single-approach-entering operation can be safely and efficiently performed. By using a kind of non-optimization methodology, a phase scheme with four entering vehicle phases, four circulating vehicle phases, and four pedestrian phases is established. Four temporal characteristics of right-of-way assignment are extracted from the design of phase scheme, based on which optimal cycle length and green splits can be determined to conditionally satisfy the temporal demands of different road users on right-of-way. Simulation experimental results indicate that the proposed signal timing plans will substantially prevent the test-bed roundabout performance from seriously deteriorating during peak periods. Also, it is recommended to integrate yield rule and traffic signalization at larger roundabouts on a time-of-day basis.
环形交叉是道路平面交叉的常见形式。作为城市道路网络的重要节点,环形交叉口可以采用两种交通控制方法:让行规则控制和交通信号控制。按照国际惯例,机动车行经让行规则控制环形交叉口时,应遵循“入环车辆让环内车辆先行、环内车辆让出环车辆先行”的规则通行。实践证明,在较低或中等机动车交通负荷水平下,与普通平面交叉口相比,让行规则控制环形交叉口更加安全、高效[ 1, 2, 3]。然而,随着机动车交通负荷水平的提高,环道车流趋于密集,车辆进出环道的难度加大,违反让行规则的现象越来越频繁,由此导致交通事故频发、通行效率降低、行人和非机动车过街难等交通问题。机动车交通高峰时段,将环形交叉口的交通控制等级由让行规则控制提升至交通信号控制成为一种必然的选择。
就环形交叉口的交通信号控制模式而言,根据交通信号灯设置方式的不同分为:①个别进口道控制;②进口道和环道全控制;根据信号配时方案生成方式的不同分为:①预设时间控制;②交通响应控制。目前,国外学者的研究多聚集于“个别进口道控制+交通响应控制”[ 4, 5, 6];国内学者的研究多聚集于“进口道和环道全控制+预设时间控制”[ 7, 8, 9, 10]。
进口道和环道全控制的四路环形交叉口可以采用2种交通组织方式:①多进口同步放行;②单进口轮流放行。多进口同步放行方式下,本向与对向的入环车辆同步获得通行权,进入环道后,直行车辆可以顺利出环,左转车辆由于受到环道信号灯的阻滞,必须在环道停止线后等待第二次通行机会方能出环。一旦环道停止线后的排队车辆过多,将严重干扰出环车辆的正常通行,导致局部环道乃至整个交叉口陷入死锁状态,进而引发区域性的全面交通拥堵。因此,多进口同步放行方式仅适用于环道排队空间较大或左转车辆较少的环形交叉口。单进口轮流放行方式下,按照顺时针的顺序依次为各个进口方向的入环车辆赋予通行权,进入环道后,左转车辆不会由于受到环道信号灯的阻滞而对直行车辆的正常通行造成干扰,基本消除了局部环道死锁的可能性。因此,单进口轮流放行方式具有普遍的适用性。此外,与多进口同步放行方式相比,单进口轮流放行方式的环形交叉口在信号配时设计时只需获取各个进口方向、各条进口道的机动车到达交通量,无需进一步区分机动车的通行方向比例,大大降低了机动车到达交通量调查工作的复杂程度,进一步增强了单进口轮流放行方式的适用性。
就通行空间资源和通行时间资源的结构性特征而言,环形交叉口明显区别于普通平面交叉口,这意味着传统的交通信号控制方法无法直接应用于环形交叉口。本文面向机动车交通高峰时段采用“进口道和环道全控制+预设时间控制”的四路环形交叉口,从相位结构设计和信号配时设计两个层面,提出一种适用于单进口轮流放行方式的交通信号控制方法,期望为环形交叉口的交通管理与控制工程实践提供理论依据和技术支持。
本文的研究环境包括:①在环形交叉口的适当位置安装有机动车信号灯和行人信号灯;②机动车交通低峰和平峰时段,关闭交通信号灯,环形交叉口采用让行规则控制;机动车交通高峰时段,开启交通信号灯,环形交叉口采用交通信号控制;③对于右转车辆不实施交通信号控制,但它们须主动避让行人、非机动车和出环车辆;④行人和非机动车实施一体化过街处理;⑤调头车辆须进入环道完成调头;⑥机动车相位的信号灯色依次为“绿灯→黄灯→红灯→绿灯”,行人相位的信号灯色依次为“绿灯→红灯→绿灯”;⑦采用RiLSA[ 11]推荐的方法计算绿灯间隔时间。
下文中涉及的符号包括: ad(R i, Kj)表示相位K j的排队头车进入环道后,在相位R i的停止线后的允许阻滞时间(s); BGZ表示相位 Z的绿灯启亮时刻(s); C表示信号周期时间(s); Co表示最佳信号周期时间(s); C( t) o表示最佳信号周期时间的第 t轮试算值(s); Cmax表示最大信号周期时间(s); Cmin表示最小信号周期时间(s); dbg(R i,K j)表示相位R i与K j的绿灯启亮时间差或相位K j的绿灯早启时间(s); EGZ表示相位 Z的绿灯结束时刻(s);F i表示行人相位的编号; GZ表示相位 Z的绿灯显示时间(s); G( t)K i表示相位K i的绿灯显示时间的第 t轮试算值(s); 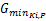
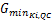
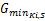
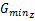

相位结构设计的目的是基于平面交叉口的道路空间条件,根据道路使用者的通行需求特征和交通信号控制设备的相关技术条件,遵循一定的原则和步骤,为不同类型、不同行走方向的道路使用者赋予通行权,提供平等的通行机会,定义通行权的传承顺序,实现通行时间资源的战略分配。
在环道数超过2条的四路环形交叉口内部,存在着大量潜在的交通冲突。随着进口道机动车信号灯、环道机动车信号灯、行人信号灯的启用,除了与右转车辆相关的交通冲突仍需利用让行规则加以分离外,其他的交通冲突均可以利用交通信号灯进行分离。
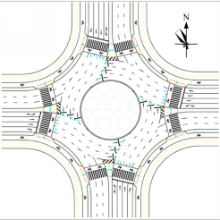
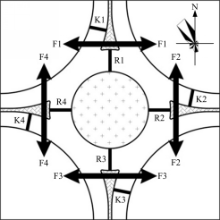
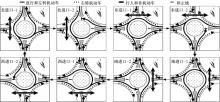
单进口轮流放行方式的四路环形交叉口具有4个进口道机动车相位(K1~K4)、4个环道机动车相位(R1~R4)、4个行人相位(F1~F4),如图1所示。进口道机动车相位和环道机动车相位采用的交通信号灯具均为圆形信号灯。归属于不同相位的道路使用者的交通冲突关系,如图2所示。存在交通冲突的相位不允许同时获得通行权。
相位组合方案用以描述一系列允许同步获得通行权的相位(或称并发相位)的组合关系,体现了一种相对稳定的通行时间资源供给状态。任意一个相位应至少存在于一个相位组合方案之中。
单进口轮流放行方式下,四路环形交叉口可能产生8种常规相位组合方案,如图3所示。进口道机动车相位与逆时针方向相邻的第1个行人相位同步获得通行权。进口道机动车相位的绿灯期间,为了充分利用局部环道的通行空间资源,允许顺时针方向相邻的第1个进口道机动车相位获得通行权。
相位显示顺序用以描述不同相位组合方案之间的更迭关系,实质上反映了冲突相位之间的通行权传承顺序,是相位结构设计的集中表现形式。
单进口轮流放行方式下,四路环形交叉口采用的常规相位显示顺序如图4所示。按照逆时针顺序,依次为各个进口道机动车相位赋予通行权。
通行权供给的时间特性是对交叉口可能采用的相位显示顺序中隐含的、关于通行时间资源供给的结构性特征的归纳和总结。根据常规相位显示顺序,得到以下4项通行权供给的时间特性:
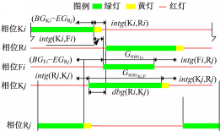
(1)进口道机动车相位与紧邻的环道机动车相位存在直接的通行权传承关系,它们的绿灯显示时间加上绿灯间隔时间之和始终等于信号周期时间,即:

(2)进口道机动车相位的绿灯显示时间与信号周期时间的数值关系如图5所示,数学表达式为:
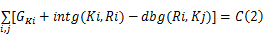
(3)根据相位显示顺序和交通冲突关系,利用式(3)(4)(5)计算进口道机动车相位、环道机动车相位的绿灯启亮和结束时刻。

(4)根据相位显示顺序和交通冲突关系,利用式(6)(7)计算行人相位的绿灯启亮和结束时刻:

信号配时设计的目的是基于平面交叉口的道路空间条件和相位显示顺序,根据通行权供给的时间特性以及控制时段内的通行时间资源需求水平,遵循一定的原则和步骤,采用一定的方法,计算信号周期时间以及各个相位、各种信号灯色的启亮和结束时刻,实现通行时间资源的战术分配。
设计流率表征了进口道机动车相位可能承载的最大通行需求。给定设计流率下,进口道的通行条件越好,饱和流率越高,满足通行需求所需的绿灯显示时间理应越少。可以利用设计流率与饱和流率的比值(即流率比)表征进口道机动车相位可能承载的最大通行需求水平。流率比的引入使得不同进口道机动车相位对于通行时间资源的原始需求具备了横向可比性。
设计饱和度是针对各个进口道机动车相位设定的最大允许饱和度,表征了该相位通行能力的期望富余程度。不同进口道机动车相位的设计饱和度可以不同。给定流率比下,设计饱和度越高,通行能力的期望富余程度越低,进口道机动车相位获得的绿灯显示时间越少。设计饱和度的建议取值为0.80、0.85、0.90、0.95。可以利用流率比与设计饱和度的比值表征进口机动车相位可能承载的最大通行时间资源需求水平,并将其作为信号配时设计的主要依据。流率比与设计饱和度的比值的引入使得不同进口道机动车相位对于通行时间资源的设计需求具备了横向可比性。
根据入环车辆(特指左转和直行车辆)的交通运行特性,进口道机动车相位的绿灯启亮后,入环车辆将以车队的形式进入环道;入环车队的头车一旦受到环道信号灯的阻滞,后续车辆将依次受到阻滞效应的影响,或减速、或停车;环道信号灯的绿灯启亮后,入环车队的头车及后续车辆依次加速至期望车速,环道信号灯对于入环车队的阻滞效应逐渐消失。
相对于逆时针方向相邻的第1个环道机动车相位,进口道机动车相位的绿灯早启时间应允许入环车队的头车经历一定的阻滞时间,同时,应确保阻滞效应不会传递至进口道停止线断面(即入环车辆通过进口道停止线时不会受到前方车辆的阻滞而减速或停车)。利用式(8)计算进口道机动车相位与逆时针方向相邻的第1个环道机动车相位的绿灯启亮时间差:
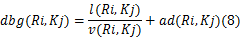
假定进口道机动车相位的绿灯前损失时间等于绿灯后补偿时间,即有效绿灯时间等于绿灯显示时间。对于任意给定的信号周期时间,利用式(2)(8)计算进口道机动车相位的绿灯显示时间总和,利用式(9)计算各个进口道机动车相位的绿灯显示时间:
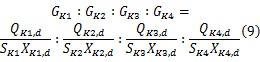
设置行人过街中央安全岛后,人行横道被分为两段,可以实施行人“同步二次过街”控制[ 11]。较高机动车交通负荷水平下,行人相位的最小绿灯显示时间应保证绿灯初期进入人行横道的行人能够到达另一段人行横道的中央位置。
与普通平面交叉口类似,进口道机动车相位的最小绿灯显示时间应保证行车安全、一定数量的入环车辆顺利通过进口道停止线以及行人和非机动车安全过街,见式(10)[ 12, 13, 14]:
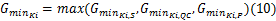
式中: 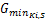
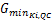
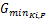
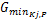
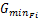
intg(R j,K j) + 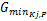
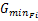

最大信号周期时间的取值不宜超过150 s。将进口道机动车相位的绿灯显示时间取为该相位的最小绿灯显示时间,利用式(2)得到最小信号周期时间的计算方法,见式(14):
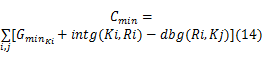
将最佳信号周期时间定义为根据通行权供给的时间特性,在信号周期时间边界值、进口道机动车相位的最小绿灯显示时间和设计饱和度的共同约束下,能够满足所有道路使用者的通行时间资源需求的最小信号周期时间。
与以往研究不同的是,本方法并未建立最佳信号周期时间的计算公式,而是要求自最小信号周期时间开始,直至最大信号周期时间,针对每个可能的信号周期时间取值,计算各个进口道机动车相位的绿灯显示时间和理论饱和度,将首先满足进口道机动车相位的最小绿灯显示时间和设计饱和度约束的信号周期时间视为最佳信号周期时间。因此,最终确定的最佳信号周期时间需要经过多轮试算,试算结果应保留小数点后1位有效数字并进行4舍5入取整操作。
若所有可能的信号周期时间取值均不满足约束条件,认为在当前的通行空间资源供给条件下,本方法无法为所有的道路使用者提供足够的通行时间资源,只能终止信号配时设计。必须通过调整交通流向和流线组织以及交通标志和标线设计,改变环形交叉口的通行空间资源供给条件,方能重新进行信号配时设计。
信号配时设计的技术流程如下:
步骤1:确定 ad(R i,K j),利用式(8)计算 dbg(R i,K j),执行步骤2。
步骤2:确定 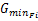
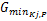
步骤3:确定 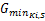
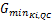

步骤4:利用式(14)计算 Cmin,令 t=1; C( t) o=Cmin,执行步骤5。
步骤5:若 C( t) o≤ Cmax,利用式(2)(9)计算 G( t)K1、 G( t)K2、 G( t)K3、 G( t)K4,执行步骤6;否则,执行步骤8。
步骤6:若 G( t)K i≥ 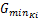
步骤7:令 BGK1 =0,利用式(3) ~(7)计算 BGK i、 EGK i、 BGR i、 EGR i、 BGF i、 EGF i,生成信号配时方案。
步骤8:调整交通流向和流线组织以及交通标志和标线设计,执行步骤1。
显然,本方法并未采用优化建模的思想,即通过对充满随机性、时变性和不确定性的道路交通系统进行一定程度的简化和抽象,将环形交叉口的通行时间资源分配问题描述成交通信号控制参数的约束优化问题,而是采用了非优化建模的思想,致力于认清道路使用者的交通运行特性,发现通行时间资源供给的结构性特征,匹配通行时间资源的供求关系,在必要的约束条件下,以一种确定性的方式,分层次、分步骤地确定交通信号控制参数,这使得本方法不仅具有科学性,还具备较强的环境适应能力,更加简单、易用。
选取典型的四路环形交叉口,在中等和较低机动车交通负荷水平下,实施让行规则控制,在较高机动车交通负荷水平下,实施单进口轮流放行方式的交通信号控制。
利用VISSIM 5.3建立仿真实验环境,测试和分析对象交叉口的性能。
对象交叉口的道路空间条件如图7所示。南北方向为主要道路,东西方向为次要道路。各条道路的路段车道数均为3条,各个进口方向具有相同的车道功能,即1条右转专用车道、2条直行专用车道、1条左转调头合用车道。
进口道采用右侧展宽,最外侧进口道的展宽段长度为50 m,展宽渐变段的长度为20 m。
中心岛的直径为35 m,进口道、出口道、环道的宽度分别为3 m/ln、3.5 m/ln、4 m/ln,人行横道的宽度为5 m,非机动车过街通道的宽度为3 m。
路段和进出口道的限制车速均为50 km/h。直行专用进口道和左转调头合用进口道的饱和流率均为1800 pcu/(h·ln)。取 l(R i,K j)≈51 m, v(R i,K j)=40 km/h。
较低、中等、较高机动车交通负荷水平下,分别在一定的抽样范围内随机选取3组机动车到达交通量,如表1所示。人行横道的单向过街行人交通量分别为100、200、400 ped/h;非机动车过街通道的单向过街非机动车交通量分别为50、100、200 cyc/h。
| 表1 机动车到达交通量的抽样结果 Table 1 Sampling results of vehicular demands pcu/h |
较高机动车交通负荷水平下,各个进口方向选取车道平均机动车到达量的最大值作为进口道机动车相位的设计流率。在此基础上,得到进口道机动车相位的流率比如表2所示。
| 表2 进口道机动车相位的流率比 Table 2 Flow ratios of entering vehicle phases |
进口道机动车相位和环道机动车相位的黄灯时间均为3 s。对象交叉口的绿灯间隔时间如图8所示。
较高机动车交通负荷水平下,令 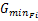
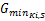
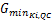
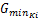
| 表3 信号配时方案 Table 3 Signal timing plans |
为了消除标准车辆折算给仿真建模带来的不便,将机动车的交通构成视为标准车辆(即车辆长度小于6 m的小型车)。
机动车的最小和最大期望速度分别为48和58 km/h。行人的最小和最大期望速度为4和6 km/h。非机动车的最小和最大期望速度为12和15 km/h。
车辆跟驰模型中,平均停车间距为2.0 m,期望安全距离的附加部分为2.5 m,期望安全距离的倍数部分为3.5 m。车道变换模型中,车辆消失前的等待时间为45 s。其他驾驶行为参数采用默认值。
仿真运行总时间为10 800 s,实验数据采集时段为900~10 800 s。针对每组交通需求进行一组仿真实验,每组仿真实验进行5次仿真运行,每次仿真运行选取的随机数分别为9、19、29、39、49。
选取交叉口的车均延误、交叉口的车均停车次数、各个进口方向的车均延误极差作为机动车相位的性能指标,选取行人和非机动车的人均延误作为行人相位的性能指标。每组交通需求下的性能指标值取为5次,仿真运行得到该性能指标值的算术平均值。仿真实验结果如表4所示。
| 表4 仿真实验结果 Table 4 Simulation test results |
较低机动车交通负荷水平下, 对象交叉口的各项性能指标值均处于低位运行态势。中等机动车交通负荷水平下,各项性能指标值均显著增大,对象交叉口的整体性能趋于恶化的态势已经形成,若不及时提升交通控制等级,局部环道乃至整个交叉口陷入死锁状态将在所难免。
较高机动车交通负荷水平下,随着对象交叉口的交通控制等级由让行规则控制提升至交通信号控制,交叉口的车均延误显著增大,但交叉口的车均停车次数和各个进口方向的车均延误极差得到了有效控制,说明本文提出的交通信号控制方法不仅能够避免机动车的通行效率再度降低,还能够均衡不同进口道机动车相位的性能;与让行规则控制相比,行人和非机动车的人均延误出现大幅增加是实施交通信号控制的必然结果,但是,本文提出的交通信号控制方法可以将人均延误值控制在一个相对较低的水平。
就环形交叉口的交通控制方法而言,让行规则控制适用于机动车交通低峰和平峰时段;交通信号控制适用于机动车交通高峰时段。对于交通信号控制环形交叉口,单进口轮流放行方式具有更为普遍的适用性,找到一种科学、有效的交通信号控制方法是促使其推广应用的重要前提。本文面向四路环形交叉口,以安全、高效地实施单进口轮流放行方式的交通信号控制为基本目的,通过深入剖析道路使用者的交通运行特性、通行时间资源供给的结构性特征、通行时间资源的供求关系,建立了相位结构设计方法和信号配时设计方法,较为系统地解决了通行时间资源的战略和战术分配问题。仿真实验结果显示,随着机动车交通负荷水平的提高,让行规则控制将难以遏制环形交叉口整体性能的显著恶化,本文提出的交通信号控制方法具有科学性、有效性、实用性,有助于显著改善机动车交通高峰时段环形交叉口的整体性能。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|






 <![CDATA[的数值关系]]>
<![CDATA[的数值关系]]>