钢-混组合梁挠度增大系数的神经网络计算方法

引用本文

魏海斌, 张仰鹏, 焦峪波, 刘寒冰. 钢-混组合梁挠度增大系数的神经网络计算方法. 2014, 44(4): 963-967
[WEI Hai-bin, ZHANG Yang-peng, JIAO Yu-bo, LIU Han-bing. Neural network-based calculation of deflection increasing coefficient of steel-concrete composite beam. Journal of Jilin University Engineering and Technology Edition, 2014, 44(4): 963-967] 复制到剪切板

Permissions

钢-混组合梁挠度增大系数的神经网络计算方法

魏海斌, 张仰鹏, 焦峪波, 刘寒冰

吉林大学交通学院,长春 130022

通信作者：焦峪波(1986-),男,讲师,博士.研究方向:桥梁智能检测.E-mail:jiaoyb@jlu.edu.cn

作者简介：魏海斌(1971-),男,副教授,博士.研究方向:道路工程.E-mail:weihb@jlu.edu.cn

基金:国家自然科学基金项目（51378236）; 吉林省科技发展计划项目(20130101039JC); 吉林大学“985工程”项目;

摘要

以简支组合梁承受均布和集中荷载为例,考虑了界面滑移效应,引入挠度增大系数的概念,以ANSYS模拟得到的组合梁有限元模型产生样本数据,将BP神经网络用于挠度增大系数的计算,推导得出了增大系数的闭合解公式。

关键词: 道路工程; 组合梁; 挠度增大系数; 神经网络; 滑移效应

中图分类号:U448 文献标志码:A 文章编号:1671-5497(2014)04-0963-05

Neural network-based calculation of deflection increasing coefficient of steel-concrete composite beam

WEI Hai-bin, ZHANG Yang-peng, JIAO Yu-bo, LIU Han-bing

College of Traffic, Jilin University, Changchun 130022, China

Abstract

A neural network-based calculation method of deflection increasing coefficient of steel-concrete composite beam is proposed. This method takes the complexity and limitation of existing methods into consideration. The simply supported composite beam under concentrated load and uniformly distributed load is taken as example. Considering the effect of interface slip, the concept of deflection increasing coefficient is put forward. Sample data of the finite element model of composite beam are generated from simulation on ANSYS. BP neural network is trained and texted first using the sample data; then, it is applied to obtain the analytical formula of the deflection increasing coefficient.

Keyword: road engineering; composite beam; deflection increasing coefficient; neural network; slip effect

Show Figures

0 引言

钢-混组合梁桥综合了传统钢结构和混凝土结构的优点,具有显著的技术特点和经济社会效益,在实际工程中得到了日益广泛的应用^{[ 1]}。挠度是正常使用状态的组合梁设计中重要的控制参数,然而钢梁与混凝土板在交界面处会产生相对滑移效应,从而引起附加挠度^{[ 2]}。根据现有研究成果,组合梁在完全剪力连接状况下由滑移效应引起的跨中截面附加挠度比例约为15%。因此,在考虑滑移效应的基础上,如何正确计算组合梁正常使用状态下的挠度就显得尤为重要。

国内外很多学者对组合梁挠度计算理论进行了研究,主要包含换算截面法、微分方程法、折减刚度法等几类^{[ 3, 4, 5, 6]}。1912年,Andrews等^{[ 3]}提出了换算截面法,该方法概念清晰、易于掌握,但忽略了滑移效应的影响,计算误差大,计算结果偏于不安全。微分方程法是基于力学理论推导得到相应的数学解析解,余志武等^{[ 4]}基于弹性体变形理论及Goodman弹性夹层假设,考虑剪切滑移影响,推导出了均布和集中荷载作用下简支组合梁挠度和界面滑移的数学解析式,通过数值模拟算例验证了该方法的有效性。李法熊等^{[ 5]}基于Gjelsvik滑移模型,通过引入纵向位移翘曲函数,推导出了悬臂及简支组合梁分别在竖向集中荷载和均布荷载作用下的挠度计算公式,并通过有限元方法验证了方法的正确性和适用性。但微分方程法计算过程复杂,难以获得封闭解,不易为设计者所掌握。折减刚度法的理论基础为梁微段理论分析得到的近似公式,聂建国等^{[ 6]}在现有研究成果基础上,推导出了不同荷载工况下组合梁因滑移引起的附加挠度计算公式,并结合实际情况对公式进行了转换。为了便于工程应用,提出了考虑滑移效应的组合梁挠度计算刚度折减法,用于现行钢结构设计规范。该方法计算意义明确、精度较高,但刚度折减系数计算过程复杂、计算量较大。

考虑到现有组合梁挠度计算方法的局限性,本文提出了一种简便且可靠的简支组合梁挠度增大系数计算方法。该方法考虑了截面滑移效应影响,以BP神经网络为计算模型,通过敏感度分析确定组合梁挠度影响参数,以简支组合梁承受集中和均布荷载为计算工况,采用有限元模拟生成训练和测试样本,通过计算得到了挠度增大系数的闭合解计算公式,为该类型桥梁的设计提供了参考。

1 挠度增大系数计算

1.1 简支组合梁挠度影响参数敏感度分析

根据现有研究成果,组合梁挠度主要由3部分组成:弹性换算截面法计算获得的挠度值;滑移效应引起的附加挠度值以及剪力滞效应引起的挠度值。为此,本文引入挠度增大系数的概念,其计算公式为:

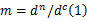
式中: dⁿ、 d^c分别为忽略和考虑滑移效应计算得到的挠度值;1 /m为组合梁结构的挠度增大系数。

为了确定挠度增大系数的神经网络计算模型所需的输入和输出参数,需要对钢-混组合梁挠度的影响因素进行分析,其基本假定包括:钢梁和混凝土材料均为理想弹性体;界面滑移与水平剪力呈正比;上部混凝土与下部钢梁在承受荷载后曲率相同,符合平截面假定;忽略配筋及掀起效应影响。简支组合梁模型如图1所示。

	Figure Option View Download New Window
	图1 简支组合梁模型Fig.1 Model of simply supported composite beam

通过理论推导得出,简支组合梁在分别承受跨中集中荷载及均布荷载工况下由滑移效应引起的跨中挠度如下式所示:

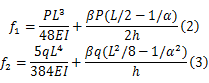
式中: P、 q分别为跨中集中荷载和均布荷载值; L为梁长; EI为截面刚度; h为梁高。

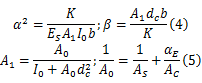
式中: A_S、 A_C分别为钢梁及混凝土翼板的面积; K为抗剪栓钉刚度; E_S为钢梁弹性模量; b为栓钉纵向间距; d_c为混凝土翼板截面中心至钢梁截面中心间的距离; I₀为等效截面惯性矩。

参考折减刚度的概念,令:

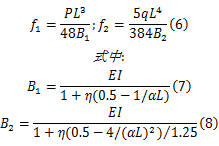
η=24 EIβ/( L² h) =24 E_S d_c pA₀ /( KhL²)(9)

由上述理论推导可知,简支组合梁由滑移效应引起的附加挠度主要影响因素为 αL及 η,本文令 λ=η/24,确定 αL和 λ为组合梁挠度的重要影响参数。另外结合参考文献[7],得知组合梁翼缘板宽度与梁长的比值( b/L)也会对组合梁挠度产生影响。因此,本文初步选定 αL、 λ和 b/L为简支组合梁挠度影响参数。

通过敏感性分析考察上述参数对 m值的影响程度,通过JAVA软件编制了敏感性分析程序,其中各参数的取值范围如下: L∈[5,20]m; αL∈[5,11]; b/L∈[0 .1,0 .35]; λ值与 αL相关联;混凝土板厚度 t∈[100,160] mm; h/L<1/16; p∈[60,100] mm;翼板混凝土强度为C40。

(1) b/L对 m值的影响规律

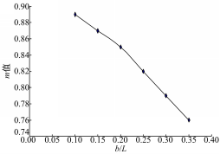
通过JAVA程序在各初始参数取值范围内随机组合,首先使得 b/L=0 .1, αL=7 .5, λ=0 .02;其次变动 b或 L使得 b/L依次取值0.1~0.35,步长为0.05,其余参数随机发生变化,使得 αL=7 .5, λ=0 .02;最后对应于每个 b/L值通过建模计算得到3组 m值,取均值后得到 b/L与 m的关系曲线,如图2所示。

	Figure Option View Download New Window
	图2 参数 b/L与 m值关系曲线Fig.2 Relationship between b/L and m

从图2可以看出: m值随着 b/L参数的增大而减小,变化幅度达到0.1,这表明挠度增大系数随着 b/L参数的增加而增大。

(2) αL对 m值影响规律

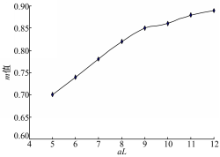
αL与 λ值彼此相关,不具备独立性,因此在敏感性分析时仅保持 b/L值为定值, m使 αL发生变化,对 m值的变化规律进行分析。同样通过JAVA程序在各初始参数取值范围内随机组合,首先使得 b/L=0 .2, αL=5时得出若干初始参数数组;其次通过保持 b/L=0 .2不变,变动其余参数使得 αL发生变化,变化步长为1;最后,对应于每一个 αL值计算得到3组 m值,计算均值得到 αL与 m的关系曲线如图3所示。

	Figure Option View Download New Window
	图3 参数 αL与 m值的关系曲线Fig.3 Relationship between αL and m

从图3中可以看出: m值随着 αL参数的增大而增大,变化幅度达到0.19,这表明挠度增大系数随着 αL参数的增大而减小。

(3) λ对 m值的影响规律

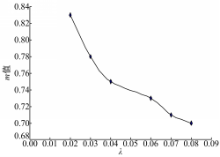
同理,首先使得 b/L=0 .2, λ=0 .02得出若干初始参数数组;其次通过保持 b/L=0 .2不变,变动其余参数使得 λ发生变化,变化步长为0.01;最后,对应于每一个 λ值计算得到3组 m值,计算均值得到 λ与 m的关系曲线如图4所示。

	Figure Option View Download New Window
	图4 参数 λ与 m值的关系曲线Fig.4 Relationship between λ and m

从图4中可以看出: m值随着 λ参数的增大而减小,变化幅度达到0.13,这表明挠度增大系数随着 λ参数的增大而增大。

通过上述敏感性分析可以得出, αL、 λ和 b/L三个参数均会对组合梁挠度增大系数产生影响,其中 αL的影响最为明显; b/L和 λ稍差。

1.2 挠度增大系数计算的神经网络结构

神经网络是具备良好自适应性的非线性计算系统,该系统通过训练样本数据的训练得出样本间内在规律,具有良好的处理复杂问题的能力^{[ 8]}。

神经网络的学习过程分为训练阶段和测试阶段两部分,网络在训练阶段通过对样本内在规律的发掘和自适应学习,不断对网络的权值和阈值进行调整,逐步降低网络模拟输出与目标值之间的相对误差,当误差达到设定的要求时,得到输入参数与输出参数之间的内在映射关系,并以各层间权值的方式储存于网络中。网络训练完成后,通过对测试样本数据的加权求和得到网络输出值,检验所建立神经网络的泛化能力^{[ 9]}。

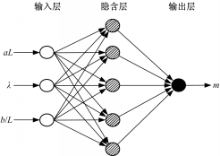
神经网络输入参数为:① αL, ②λ, ③b/L;输出参数为: m=dⁿ/d^c。

神经网络的隐含节点传递函数选用Sigmoid函数,输出层选用线性函数,训练算法为Levenberg-Marquart算法。本文使用的神经网络基本结构如图5所示。

	Figure Option View Download New Window
	图5 神经网络结构Fig.5 Structure of neural networks

2 挠度增大系数计算结果及讨论

采用Solid45单元来模拟结构混凝土,采用非线性壳单元Shell43模拟钢梁,采用combin39弹簧单元模拟栓钉。

通过有限元模拟产生的50组样本数据作为神经网络的训练样本,得到 αL、 λ和 b/L与 m值之间的内在非线性关系。另外11组样本为测试样本,验证神经网络的仿真效果,其计算结果如表1所示。

表1 神经网络测试样本仿真结果分析 Table 1 Simulation results of neural network for test samples

从表1可以看出,神经网络仿真结果与理想输出之间的最大相对误差为2.99%,这表明本文所建立的神经网络结构能够对测试样本进行良好的预测,具备很强的泛化能力,其输出结果可以用于挠度增大系数的计算。

根据神经网络的计算原理,通过层间权重及阈值矩阵,最终计算得到钢-混组合梁挠度增大系数的计算公式。组合梁在集中及均布荷载作用下的权值、阈值如表2和表3所示。

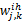
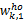
在表2、表3中, 表示输入层第 j个神经元与隐含层第 k个神经元之间的权重值; 表示隐含层第 k个神经元与输出层神经元之间的权重; θ_k表示隐含层第 k个神经元阈值。

表2 均布荷载下神经网络层间权值( w)与阈值( θ) Table 2 Weight and bias values for neural network of uniform load

表3 集中荷载下BP网络层间权值与阈值表 Table 3 Weight and bias values for neural network of concentrated load

由表2可以得到简支组合梁在均布荷载下的 m值计算公式:

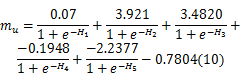
式中: H₁ =b/L×125 .86 +αL×( -4 .0878) +λ×126 .755 -19 .6988; H₂ =b/L×1 .1336 +

αL×0 .1849 +λ×9 .10 -2 .8893; H₃ =b/L×

( -149 .59) +αL×( -2 .0956) +λ×33 .6955 +

66 .3351; H₄ =b/L×0 .1887 +αL×0 .12 +λ×

( -32 .5674) -0 .2369; H₅ =b/L×1 .4144 +αL×0 .2479 +λ×11 .4401 -3 .3755。

因此,可以计算得到简支组合梁在均布荷载下的挠度增大系数 μ_u=1 /m_u。

由表3可以得到简支组合梁在集中荷载下的 m值计算公式:

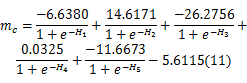
式中: H₁ =b/L×0 .4996 +αL×0 .0296 +λ×

12 .8380 -2 .7386; H₂ =b/L×( -28 .1096) +αL×( -7 .6838) +λ×72 .3809 -47 .2017; H₃ =b/L×( -30 .5204) +αL×( -7 .5095) +λ×61 .5285 +47 .0132; H₄ =b/L×( -0 .0090) +αL×

0 .5161 +λ×( -33 .3117) -4 .1052; H₅ =b/L×35 .6508 +αL×8 .2481 +λ×50 .5491 -55 .8456。

同理,也可以计算得到简支组合梁在集中荷载作用下的挠度增大系数 μ_c =1 /m_c。

3 结束语

针对钢-混简支组合梁正常使用阶段的挠度计算问题,考虑界面滑移效应影响,通过引入挠度放大系数概念,采用神经网络为计算模型,得到了挠度增大系数的闭合解析式。该方法通过有限元模拟获取训练及测试样本,针对满足测试要求的神经网络模型提取权值和阈值,最终推导得出了简支组合梁在跨中集中荷载和均布荷载作用下的挠度增大系数计算公式,为该类型桥梁的设计提供了参考。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	欧阳煜, 刘慧, 杨骁. 考虑粘结层滑移效应的组合梁弯曲[J]. 工程力学, 2012, 29(8): 215-222. Ouyang Yu, Liu Hui, Yang Xiao. Bending of composite beam considering effect of adhesive layer slip[J]. Engineering Mechanics, 2012, 29(8): 215-222. [本文引用:1] [CJCR: 0.583]
[2]	Faella C, Martinelli E, Nigro E. Stell and composite beams with flexible shear connection: exact analytical expression of the stiffness matrix and application[J]. Computer and Structures, 2002, 80(11): 1001-1009. [本文引用:1] [JCR: 1.509]
[3]	Andrews E S. Elementary Principles of Reinforced Concrete Construction[M]. London: Scott, Greenwood and Sons, 1912. [本文引用:2]
[4]	余志武, 蒋丽忠, 李佳. 集中荷载作用下钢-混凝土组合梁界面滑移及变形[J]. 土木工程学报, 2003, 36(8): 1-6. Yu Zhi-wu, Jiang Li-zhong, Li Jia. The interface slip and deformatin of steel-concrete compostie beams under concentrated loads[J]. China Civil Engineering Journal, 2003, 36(8): 1-6. [本文引用:2] [CJCR: 0.921]
[5]	李法雄, 聂建国. 钢-混凝土组合梁剪力滞效应弹性解析解[J]. 工程力学, 2011, 28(9): 1-8 Li Fa-xiong, Nie Jian-guo. Elastic analytical solutions of shear lag effect of steel-concrete composite beam[J]. Engineering Mechanics, 2011, 28(9): 1-8. [本文引用:2] [CJCR: 0.583]
[6]	聂建国, 沈聚敏. 钢-混凝土简支组合梁变形计算的一般公式[J]. 工程力学, 1994, 11(1): 133-137. Ni Jian-guo, Shen Ju-min. A general formula for predicting the deflection of simply supported composite steel-concrete beams with the consideration of slip effect[J]. Engineering Mechanics, 1994, 11(1): 133-137. [本文引用:2] [CJCR: 0.583]
[7]	聂建国, 李法雄, 樊健生, 等. 钢-混凝土组合梁考虑剪力滞效应实用设计方法[J]. 工程力学, 2011, 28(11): 45-51. Ni Jian-guo, Li Fa-xiong, Fan Jian-sheng, et al. Practical design method for steel-concrete composite beam considering shear lag effect[J]. Engineering Mechanics, 2011, 28(11): 45-51. [本文引用:1] [CJCR: 0.583]
[8]	朱凯, 王正林. 精通Matlab神经网络[M]. 北京: 电子工业出版社, 2010. [本文引用:1]
[9]	刘寒冰, 焦峪波, 程永春, 等. 基于模态曲率理论及神经网络的简支梁桥损伤识别[J]. 吉林大学学报: 工学版, 2011, 41(4): 963-967. Liu Han-bing, Jiao Yu-bo, Cheng Yong-chun, et al. Damage identification for simply supported beam bridge based on modal curvature theory and neural network[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(4): 963-967. [本文引用:1] [CJCR: 0.701]

2012

0.0

0.583

. 2012, 29(8):215-222 DOI:10.6052/j.issn.1000-4750.2010.12.0927

Bending of composite beam considering effect of adhesive layer slip

Department of Civil Engineering, Shanghai University, Shanghai 200072, China

For a composite beam with a adhesive layer, the general nonlinear governing equations for a large deflection are established with the assumption that the adhesive layer only exists the shear deformation along the axial direction. And it is revealed that the deflections at the sub-beam axial lines of the composite beam are equal only in sense of the first order approximation. Then, by linearization technique, the coupled governing equations for linear bending of the composite beam are obtained from the above nonlinear equations under the condition of the Euler-Bernoulli beam deformation, in which the basic unknowns are its deflection and its axial displacement. The coupled equations derived can be degenerated into the governing equations for the classical composite beam and stop log, respectively. Finally, the linear bending of the cantilever composite beam, subjected to a concentrated load at its free end, is investigated, and the analytical solutions are obtained. The curves of the deflection of the composite beam, the slip displacement and shearing force of the adhesive layer at the free end versus the shear modulus and thickness of the adhesive layer are shown in figures, and the parameters study is conducted. It is shown that the adhesive-layer’s thickness and shear modulus have great influences on the deflection of a composite beam and the slip displacement of an adhesive layer, and a little influence on the shear force of the adhesive layer.

针对粘结型组合梁,在粘结层仅沿轴向剪切变形的假定下,给出了组合梁大挠度弯曲的一般非线性控制方程,指出仅在一阶近似下,组合梁子梁的轴线挠度相等.其次,在Euler-Bernoulli 梁变形的条件下,通过线性化方法,由上述非线性控制方程得到以挠度和轴向位移为基本未知量的组合梁线性弯曲耦合控制方程,该耦合方程组可分别退化为经典组合梁和叠梁的控制方程.最后,分析了悬臂组合梁在端部集中力作用下的线性弯曲,得到了问题的解析解,给出了不同梁长下组合梁自由端挠度、粘结层滑移位移和剪切应力等随粘结层剪切模量和厚度的变化曲线,进行了参数分析,结果表明：粘结层厚度和剪切模量对组合梁挠度和粘结层滑移有较为显著的影响,而对粘结层剪力影响很小.

... 0 引言钢-混组合梁桥综合了传统钢结构和混凝土结构的优点,具有显著的技术特点和经济社会效益,在实际工程中得到了日益广泛的应用^[1] ...

2002

1.509

0.0

. 2002, 80(11):1001-1009 DOI:10.1016/S0045-7949(02)00038-X

Stell and composite beams with flexible shear connection: exact analytical expression of the stiffness matrix and application

Abstract A displacement-based finite element model for the analysis of steel and concrete composite beams with flexible shear connection is presented in this paper. No approximations are introduced in the displacement field, because the stiffness matrix and the fixed-end nodal force vector are directly derived from the “exact” solution of Newmark's differential equation. Therefore, the present finite element may employ only one element per member, because internal nodes are only needed for variations of geometrical and mechanical properties and in the presence of concentrated forces. A simple criterion to establish if partial interaction effects may be neglected in the analysis of composite beams is also suggested.

... 挠度是正常使用状态的组合梁设计中重要的控制参数,然而钢梁与混凝土板在交界面处会产生相对滑移效应,从而引起附加挠度^[2] ...

1912

0.0

... 国内外很多学者对组合梁挠度计算理论进行了研究,主要包含换算截面法、微分方程法、折减刚度法等几类^[3,4,5,6] ...

... 1912年,Andrews等^[3]提出了换算截面法,该方法概念清晰、易于掌握,但忽略了滑移效应的影响,计算误差大,计算结果偏于不安全 ...

2003

0.0

0.921

... 国内外很多学者对组合梁挠度计算理论进行了研究,主要包含换算截面法、微分方程法、折减刚度法等几类^[3,4,5,6] ...

... 微分方程法是基于力学理论推导得到相应的数学解析解,余志武等^[4]基于弹性体变形理论及Goodman弹性夹层假设,考虑剪切滑移影响,推导出了均布和集中荷载作用下简支组合梁挠度和界面滑移的数学解析式,通过数值模拟算例验证了该方法的有效性 ...

2011

0.0

0.583

. 2011, 28(9):1-8

Elastic analytical solutions of shear lag effect of steel-concrete composite beam

(Department of Civil Engineering, Tsinghua University, Beijing 100084, China)

An analytical model is proposed for steel-concrete composite beams accounting for not only the slip between the steel beam and concrete slab but also the shear lag effect in the concrete slab. In order to considering the shear lag effect, a warping shape function accounting for the non-uniform transverse distribution of longitudinal displacements in the concrete flange is introduced into Gjelsvik’s model. Then analytical solutions for the cases of simply supported composite beam under uniform distribution load and cantilever composite beam under end concentrated load are derived. From the comparison of the results of FEM and analytical solutions, it is shown that the shear lag effect in composite slab and slip effect in the interface are coupled. The shear lag effect decrease when reducing shear stiffness of interface, while slip deformation and deflection of composite beam increase. The thickness of concrete slab has little impact on the shear lag effect. It is also indicated that there is apparently difference between the distributions of effective width coefficient along the beam axis under different load type.

基于Gjelsvik组合梁滑移模型中引入描述组合梁翼板横向非均匀分布的纵向位移翘曲函数，建立一个能够同时考虑界面滑移和翼板剪力滞双重效应的钢-混凝土组合梁模型，并推导了简支组合梁在均布荷载和悬臂梁在梁端集中荷载作用下的解析解。采用有限元方法验证了理论模型和解析解的正确性和适用性。算例分析表明，组合梁的剪滞效应和界面滑移效应存在耦合关系，界面剪切刚度的降低使剪力滞效应得到缓解，但是界面滑移和组合梁的挠度相应增大，翼板厚度对组合梁剪力滞效应影响不明显，不同荷载类型所产生的有效宽度系数沿梁轴方向的分布有显著差别。

... 国内外很多学者对组合梁挠度计算理论进行了研究,主要包含换算截面法、微分方程法、折减刚度法等几类^[3,4,5,6] ...

... 李法熊等^[5]基于Gjelsvik滑移模型,通过引入纵向位移翘曲函数,推导出了悬臂及简支组合梁分别在竖向集中荷载和均布荷载作用下的挠度计算公式,并通过有限元方法验证了方法的正确性和适用性 ...

1994

0.0

0.583

. 1994, 11(1):133-137

A general formula for predicting the deflection of simply supported composite steel-concrete beams with the consideration of slip effect

Hunan University

This paper presents a method for modifying the designing structural parameters of a bridge structure so that the bridge structure will freely vibrates at prescribed frequencies and modes. Based upon the orthoganal and characteristic equation of modal theory, the equations for solving the modified structural parameters are derived and then, are solved by using of generalized inverse technique. A practical example is given to show the efficiency of the proposed method for resolving the inverse dynamic modification problems of bridge structures.

本文研究了修改桥梁结构设计参数,使其自振周期和振型满足预先给定设计要求的动力特性修改过问题,提出了一种求解方法。在建立桥梁结构有限元动力学模型的基础上,该方法利用模态理论的正交关系与特征关系导出动力特性修改逆问题求解方程,然后,用矩阵广义逆技术求解。应用实例表明,本文方法具有较高的精度,是一种简便有效的桥梁结构动力特性修改逆问题的求解方法。

... 国内外很多学者对组合梁挠度计算理论进行了研究,主要包含换算截面法、微分方程法、折减刚度法等几类^[3,4,5,6] ...

... 折减刚度法的理论基础为梁微段理论分析得到的近似公式,聂建国等^[6]在现有研究成果基础上,推导出了不同荷载工况下组合梁因滑移引起的附加挠度计算公式,并结合实际情况对公式进行了转换 ...

2011

0.0

0.583

. 2011, 28(11):45-51

Practical design method for steel-concrete composite beam considering shear lag effect

1. Department of Civil Engineering, Tsinghua University, Beijing 100084, China;2. Beijing Municipal Engineering Research Institute, Beijing 100037, China

Shear lag effect has significant effect on stress and deflection of composite beams. According to the elastic analytical model of composite beams, stress and deflection analytical solutions for the cases of simply supported composite beams and cantilever composite beam under uniform distribution load and concentrated load are derived by ignoring slip effect in the interface. By introducing effective flange width and effective sectional rigidity, practical design methods for considering shear lag effect of composite beam are presented, and the results calculated by these methods have good agreement with those obtained from analytical solutions. By comparing different design methods for composite beam considering shear lag effect from different countries, the simple practical design method presented in this research is found to have high accuracy despite of its simplicity.

钢-混凝土组合梁翼板剪力滞效应对组合梁截面应力和变形产生重要影响。基于组合梁弹性理论分析模型，忽略界面滑移效应，推导了简支和悬臂组合梁在均布和集中荷载作用下的应力和变形解析解。通过引入翼板有效宽度和截面有效刚度的两种简化设计方法分别考虑翼板剪力滞效应对组合梁截面应力和变形的影响。用该文提出的简化设计方法计算考虑剪力滞效应时组合梁截面应力和变形与解析结果吻合良好。通过比较分析各国规范关于组合梁剪力滞效应的设计方法，该文提出的简化设计方法具有精度高、计算方法简单等优点。

2010

0.0

... 2 挠度增大系数计算的神经网络结构神经网络是具备良好自适应性的非线性计算系统,该系统通过训练样本数据的训练得出样本间内在规律,具有良好的处理复杂问题的能力^[8] ...

2011

0.0

0.701

. 2011, 41(4):963-967

Damage identification for simply supported beam bridge based on modal curvature theory and neural network

College of Transportation, Jilin University, Changchun 130022, China

A two-step method was proposed to identify the damage of the simply supported beam bridge with multiple girders. The method identifies the structure damage using the modal curvature difference and the neural network technique to avoid the disadvantages of each single method. A numerical example was provided for a simply supported T beam bridge with five girders to verify the feasibility of the method, and the results show that this two-step method is effective to locate damage and evaluate the damage degree.

针对多片简支梁桥损伤识别问题，提出了一种分步识别法。该方法综合运用模态曲率差及神经网络技术对结构损伤进行识别，能够有效地发挥两种方法的优点。最后以一座五片简支T梁桥为算例进行了数值模拟。模拟结果表明，该方法可以准确识别结构的损伤位置及损伤程度，是一种行之有效的简支梁桥损伤识别方法。

... 网络训练完成后,通过对测试样本数据的加权求和得到网络输出值,检验所建立神经网络的泛化能力^[9] ...