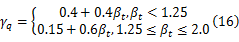作者简介:姜封国(1977-),男,副教授,博士.研究方向:结构可靠性分析和防灾减灾.E-mail:jiangfg123@126.com
综合考虑抗力折减和火灾荷载系数,对受火钢柱的可靠性进行了分析。通过具体算例来确定火灾和钢柱的温度以及钢柱的承载力,影响结构反应的大量特定参数都被视为随机变量,包括火灾荷载、建筑面积与火灾构件总面积的比率、开放性参数、构件的热吸收率、厚度、绝缘体的热传导率、恒荷载、活荷载,钢的力学和几何特性(屈服强度、截面面积等)也被视为随机变量。选择一榀框架进行受火钢柱的可靠性分析,分析结果表明,承载力折减系数和火灾荷载系数不是常量,随建筑物中防火系统和构件尺寸的不同而变化。
The reliability of steel columns exposed to fire is analyzed, in which the capacity reduction and fire load factors are considered. A case study for evaluating the fire and steel column temperatures and the load capacity of the steel column is carried out to analyze the structural reliability of the column. The parameters affecting the structural reliability are treated as random variables, such as the fire load, dead load, live load, thermal absorptivity of structural boundaries, thickness, density and thermal conductivity of the insulation, ratio of floor area to the total area of the fire compartment, opening factor, and so on. The mechanical and geometric properties of the steel column (e.g. yield strength, elastic modulus, cross-section area, etc.) are also taken as random variables. The fire protection systems are related to the probability of fire occurrence. The retailed analysis results show that the capacity reduction and fire load factors should not be treated as constants in all design situations; they should be varied with fire protection system in the building and the compartment size.
一般钢结构在正常工作条件下,其温度绝对值不高,波动不大,按照现行规范[ 1]进行设计,可保证结构安全,并能满足建筑物的使用功能要求,但是钢材的物理及机械性能对高温很敏感。高温作用后,钢的屈服强度和弹性模量随温度的升高而下降,从而导致结构构件会有不同程度损伤,其承载力相应地也会降低[ 1, 2, 3],所以,对于高温作用后的钢结构进行合理的可靠性评估、鉴定,从而采取科学的加固方法尽量快速地恢复建筑物的原有使用功能是一个重大问题。国家标准《建筑结构可靠度设计统一标准》(GB50068-2001)规定[ 4]:结构构件的可靠度宜采用可靠性指标来度量。大连理工大学的赵国藩等[ 5, 6, 7]分别讨论了工程结构在承受反复荷载作用下钢结构的疲劳失效模式、考虑钢结构经济优化设计的可靠性分析方法。但目前基于受损钢结构的可靠度研究的文献很少,尤其是火灾后受损钢结构的抗力、火荷载作用效应及结构安全性、耐久性评估的理论研究较少。
在工程方法中,火灾中强度设计的确定需要满足的条件是:应用荷载效应不大于结构承载力,即:
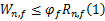
式中: Wn,f是设计条件下火灾时的应用荷载效应; Rn,f是火灾时的名义承载力,依据火灾时钢构件的温度来获得; φf是承载力折减系数。
影响结构可靠性的因素归纳为两个综合量:即结构构件的荷载效应和抗力。本文对受火轴心受压钢柱进行可靠性分析,分析过程中综合考虑了承载力折减系数和火灾荷载系数。
火灾中构件的荷载效应组合值 Wu为:
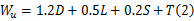
式中: D、 L和 S分别是名义恒荷载、活荷载和雪荷载; T是由火灾本身引起的荷载,特别是由于周围结构阻止热膨胀引起的荷载。
通过对文献[1]和AISC设计规范的比较,得出AISC规范在高温下是非保守的,尤其是在钢柱长细比为40~100、温度高于500 ℃条件下,例如,在500 ℃时,由AISC规范预测的名义强度比文献[1]高出60%。本文采用文献[2]提出的方程,该方程与文献[1]和AISC规范有相同的预测强度,方程为:
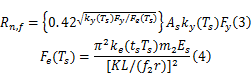
式中: Rn,f是火灾作用下钢柱的承载力; As是横截面面积; KL是有效长度; r是弯曲轴力作用下的旋转半径; ky( Ts) Fy是折减的屈服强度; ke( Ts) Es是折减的屈服强度弹性模量; Fy和 Es分别是常温下屈服强度和弹性模量; ky( Ts)和 ke( Ts)分别是弹性模量和屈服强度的折减系数,在不同温度作用下它们的值由文献[3]给出。
从式(3)(4)中可以看出,高温作用下钢柱的承载力是依据钢所受的最高温度 Ts来决定的,所以本文将评估火灾作用下钢柱所受的温度。
钢构件的温度可以应用有限元软件SAFIR、ANSYS等进行模拟,大多数设计规范允许应用简单的热分析方法评估钢构件温度,例如集中热承载力方法。热平衡微分方程可以写成:
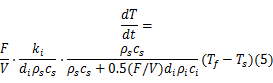
式中:d T/d t是钢构件温度变化率; F是构件每单位长度的表面积(m2); V是构件每单位长度的体积(m3); ρs cs是钢的热容量; di是绝缘体的厚度(m); ki是热传导系数(W/(m·K)); Tf是火灾的温度(℃)。
式(5)也可以写成有限差分的形式,钢构件的温度可以通过任何有限差分的方法求得。然而,对于应用在可靠性分析中的功能函数的抗力计算,钢构件的温度采用式(5)的近似解是最适合的,近似解在文献[8]中给予了详细的解释。
承载力折减系数和火灾荷载系数的应用可以通过下面步骤来实现:
(1)获得统计参数:包括钢筋屈服强度设计参数、火灾荷载的均值、变异系数等。
(2)建立一个适当的功能函数。
(3)调整抗力模型:给出计算承载力时设计方程和火灾实验测出某些系数的差异。
(4)选择目标可靠性指标 βt,该可靠性指标可以反映失效概率是一个相对安全的措施。
(5)通过可靠性分析来计算承载力折减系数和火灾荷载系数。
影响钢柱火灾设计的关键参数被看作随机变量,它们的均值、协方差和分布类型在表1中给出。
| 表1 火灾设计参数的分布、均值和协方差 Table 1 Mean,COV and distributions of fire design parameters |
表1中的 Lapt的协方差根据辅助面积[ 9]确定,其值如下: Lapt =0 .82[1 -0 .00113( At -56)],5 .2≤ At≤31 .2144; Lapt =0 .56[1 -0 .0001865( At -336)], At≥31 .2144。 bNWC为标准重量混凝土的热吸收率; bDWC为轻质混凝土的热吸收率; bg为石膏板的热吸收率; bmix为标准重量混凝土和石膏板混合构件的热吸收率; Di为石膏板绝缘体的密度。恒荷载和任意时点活荷载的统计在文献[10-11]中给出,火灾荷载的统计由文献[12]给出。文献[11]得出的钢构件失效通常是发生在400 ℃~600 ℃,本文给出的400 ℃~600 ℃作用下的石膏板材料热传导的统计分析如表2所示[ 13],它们均服从正态分布。
| 表2 常温下设计参数的均值和协方差 Table 2 Mean and COV of room temperature design parameters |
3.2.1 荷载组合
文献[11]忽略了火灾荷载和活荷载、雪荷载、风荷载和地震荷载的耦合概率。因此,在火灾作用下进行可靠性分析时考虑任意时点的活荷载和恒荷载的组合是合理的。可靠性分析的荷载效应可以表示为:
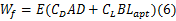
式中: CD、 CL是荷载效应的确定性影响系数,该荷载效应是由荷载强度转变的(例如弯矩、剪力、轴力); A、 B是引起荷载效应的不确定性随机变量; E是反映结构分析不确定的随机变量。
D和 Lapt在表1中给出,参数 A、 B和 E的统计如下: μA=1 .0 COVA=0 .04; μB=1 .0 COVB=0 .02; μE=1 .0 COVE=0 .05。
3.2.2 钢柱的承载力
火灾作用下钢柱承载力可以通过修改名义承载力式(3)和式(4)来求得:
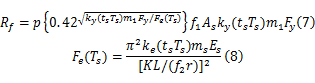
式中: p、 fi、 mi和 ts是非量纲随机变量,定义如下: p是“功能系数”,用来平衡由火灾试验测得的柱轴心承载力和由式(3)预测的名义承载力之间的差异,它可以平衡由假设引起的误差,例如,通过横截面的统一温度,完全的弹塑性行为等; fi是平衡横截面面积和横截面旋转半径之间的不确定的随机变量,即名义截面面积和标准截面的回转平面半径与实际值是不同的; mi是平衡材料特性不定性的随机变量,例如,设计规范给出的钢筋屈服强度值和弹性模量值与实际值是不同的; ts是随机修正系数,用来平衡由模型获得钢构件温度与实际试验测得的温度之间的差异。
3.2.3 极限状态方程
火灾作用下钢构件可靠性分析的极限状态方程如下:
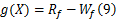
式中: X是变量,代表所有随机设计参数,钢构件在火灾作用下的失效概率表示为 pf, pf =P[ g( X) <0]。
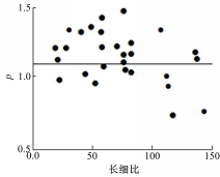
为了平衡由试验室测得的钢柱轴心承载力和由式(3)预测得到的柱轴心承载力之间的差异,文中利用文献[14-15]给出的试验结果来定义功能系数 p,文献[14]的结果是通过对18个长细比为25~102的钢柱进行试验测得的屈服强度,文献[15]的结果是通过对20个长细比为20~140的钢柱进行试验得到的。 p(测得的轴心承载力同名义承载力之比)和长细比之间的关系通过图1给出, μp=1 .1, COVp=0 .18,符合正态分布。
利用简化质量集中的方法来评估构件截面的最高温度分布,这与真实火灾试验测得的方法会有差异,这中间的差异用模型误差 ts来表示,本文假设柱的每个面都受到火灾作用。
钢构件的试验温度已经被许多学者研究过,但大部分试验测试都用标准火灾来代替真实火灾,这样就不能用来评估真实火灾引起的误差。文献[16]进行了9个真实火灾试验,记录了完全暴露在火灾中的钢构件温度和火灾中被保护的钢构件温度,为了呈现出所有真实火灾的可靠性,实验施加了一定程度的火灾荷载(380~760 MJ/m2),不同的开放系数( Fv =0 .0029 -0 .062 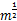
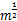
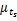
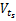
文献[17]指出,在安全系数火灾设计中,应该考虑发生概率很少的严重火灾。给出火灾防护系统,例如自动洒水器、报火器等,减少严重火灾发生的概率,从而降低失效概率。安全系数依靠目标可靠性指标 βt的选择,与失效目标概率有关,因此,可以通过减少目标可靠性指标来降低火灾作用下的失效概率。
目标可靠性指标 βt可以通过火灾防护系统的有效性来进行计算,计算方法在文献[9]中给出,文献[9]还给出为了减少严重火灾发生概率时对于不同防护系统有效性的相应值,应用该方法,评估某办公楼典型受火构件的 βt,发现对于承载力折减系数和火灾荷载系数法, βt值为0~2.0时是合理的。因为不同严重程度的火灾发生的概率不同,火灾防护系统也是不同的。所以, βt在不同设计情形下也是不同的。
3.6.1 每个设计参数的分项安全系数
对于正态分布随机变量设计参数 X,分项安全系数是由一次二阶矩法(FORM)求出:
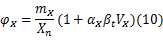
式中: mX、 VX、 αX分别是名义值 X的均值、协方差和设计点的方向余弦。
对于正态随机参数(如对数分布),分项安全系数可以由式(10)计算。式(10)中所有的参数除了方向余弦都可以从前文求得,方向余弦可以通过可靠性分析来求得。
3.6.2 分项安全系数和承载力折减系数的结合
为了设计方便,除了火灾荷载,所有设计参数的变量都是通过承载力折减系数来体现,而不是通过分项安全系数来体现。火灾荷载的设计参数中的分项安全系数可以通过式(10)与承载力折减系数 φf组合求得, φf的表达式为:

式中: Fe( Ts) = 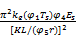
火灾荷载是火灾设计中一个重要参数,由于它的不确定性对设计的安全性有重要的影响。因此,在整体安全性中火灾荷载的变异性可以通过具体的火灾荷载的分项安全系数来解释。在前文中提到,AISC规范中建议,如果结构安装了可靠的喷淋系统,火灾荷载可以减小到60%,建议用独立的火灾安全系数。
3.6.3 理想的承载力折减系数和火灾荷载系数
承载力折减系数可以通过式(11)求得,火灾荷载系数可以通过式(10)求得,对于不同设计情形求法不同。为了设计方便,理想的状态是对于不同的设计情形都有单独的理想承载力折减系数。另外,对于钢柱的火灾设计,AISC设计规范建议恒荷载系数和活荷载系数分别用1.2和0.5。本文采用文献[18]的方法来确定承载力折减系数和火灾荷载系数。
每种设计情形下名义承载力都基于FORM(一次二阶矩)法给出:
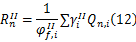
式中: 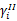
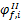
与建议恒荷载和活荷载系数相应的名义承载力为:
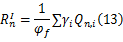
式中: γi对于恒荷载和活荷载分别是1.2和0.5, φf是最佳承载力折减系数,它的值在式(13)中可以通过减小目标功能函数来选取:
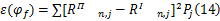
式中: Pj是第 j种设计情形下的重量分配,本文认为在每种设计情形下重量分配是相同的。
本文选取了20个长细比为25~200、轴心荷载承载力为133~10675 kN的钢柱来进行可靠性分析。较小的承载力是代表典型办公楼上层,较大的承载力代表下层。活荷载与恒荷载比率为0.5~5.0,承载力折减系数为1.0,柱荷载比率(火灾作用下应用荷载和常温下名义承载力的比率)范围为0.35~0.66。
本文应用Matlab软件进行可靠性分析,该方法是一种常用目标结构可靠性方法,可以用来运行不同类型的可靠性分析,包括FORM,对于特定设计情况下FORM分析结果包括可靠性指标、失效概率、失效/设计点的所有设计参数值、每个设计参数设计点的方向余弦。
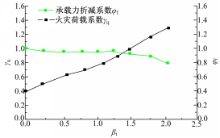
对于20种柱的每种设计情形,运用FORM法对应用式(9)中给定的功能函数进行分析,通过可靠性分析获得的方向余弦,由式(10)获得每种设计情形下每个设计参数的分项安全系数。分项系数通过式(11)即可得到单独的承载力折减系数。因此,可以获得20个不同的承载力折减系数,通过3.6.3节描述的优化程序可以获得单独的优化承载力系数,由于承载力折减系数是针对 βt为0~2时获得的,所以程序对于每个 βt都要重复,可以通过小程序来获得每个 βt对应的火灾荷载系数。
βt -φf关系曲线如图2所示, φf的值可以通过下式求得:
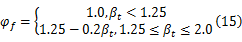
某八层开放式办公大楼,楼面面积为100 m2,内部为3.65 m长的钢柱,所受恒荷载为178 kN,活荷载为360.3 kN,柱截面为5703 mm2,回转半径为34.8 mm钢屈服强度为345 MPa,弹性模量为20000 MPa,混凝土密度 ρc=2000 kg/m3,比热 cc=840 J/(kg·K),热传导系数 λc=0.8 W/(m·K),构件每表面积单元火灾荷载为196 MJ/m2。
(1)火灾作用下构件承载力为:
Wu,f =1 .2 D+0 .5 L=1.2×178+0.5×360.3=393.75 kN
(2)柱的承载力
选择目标可靠性指标:办公楼火灾发生的概率为4×10-7(m2·年),100 m2构件55年服役寿命内火灾发生的概率为:
p1 =100 ×55 ×4 ×10 -7 =0 .0022
自动喷淋失效概率为:
p2 =0 .2
火灾发生的概率为:
ps= p1· p2=0.000 44
服役建筑物目标失效概率为[ 6]:
pt =7 .23 ×10 -5
目标可靠性指标:
βt =Φ-1(1 -pt /ps) =1 .0,本文 βt是按着文献[10]的方法确定的。
选择适当的承载力折减系数和火灾系数: φt =1 .0; γq =0 .4 +0 .4 βt =0 .8。名义火灾荷载为196 MJ/m2;构件整体表面积 At =346 m2;窗户高度 Hv =1 .5 m,窗户总面积 Av =9 m2;开放系数 Fv =Av 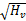
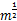

假设绝缘体的厚度(石膏板)为15 mm;火灾荷载= γq×名义火灾荷载=0.80×196=156.8 MJ/m2。
应用该火灾荷载和前文给出的其他参数,火灾温度可以通过火灾模型[ 19]求出。应用式(5)可以算得钢所经历的温度最大值: Ts,max =606 .5 ℃,屈服强度的折减系数 ky( Ts) =0 .454,弹性模量的折减系数 ke( Ts) =0 .298,柱的名义承载力可以通过式(3)(4)和承载力折减系数 φt =1 .0得出: Rn,f=201.6 kN。由于 Rn,f <Wu,f,隔热厚度不够,执行下一个厚一些的隔热厚度。本文迭代4次后,得到的厚度是21.5 mm。该数值与试验值[ 15]匹配,所以可以证明本文方法的合理性。在这里,需要的隔热厚度是通过迭代得到的,应用同一种方法,钢柱的失效温度和相应的抗火时间也可以通过给定的隔热厚度计算出来。
综合考虑了承载力折减系数和火灾荷载效应系数,并对受火后钢柱进行了可靠性分析,通过目标函数的可靠性指标来调整热力耦合钢柱的影响系数。由可靠性分析得出:承载力折减系数和火灾系数对于所有的设计情形不可能是常量,而是根据建筑物的火灾防御系统和构件尺寸进行变化的。当建筑物采用积极的火灾防御系统,对于典型的火灾构件尺寸来说,火灾荷载系数可以适当降低。本文的结论可对受损后热-力耦合钢柱的破损评估提供一定的理论支持。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|