作者简介:张立勋(1962-),男,教授,博士.研究方向:机电一体化技术.E-mail:lixunzhang2002@yahoo.com.cn
为提高立轴风力机的启动能力,提出了适宜低尖速比运行的桨距角变化规律,并设计了一种变桨执行机构以实现多组叶片的统一变桨距控制。从变桨执行机构、翼型选择、风轮结构和控制系统等方面介绍样机设计原理,并进行了样机性能实验。结果表明:对称翼型厚度为15%时最佳,而非对称翼型的最大厚度不超过10.4%;实验数据与理论值变化趋势一致,理论值相比实验数据高出20%~30%;通过增加上盘面顺风区叶片迎风面积可以提高启动能力。
In order to improve the self-starting capacity of Vertical Axis Wind Turbine (VAWT), the variation rule of blade pitch angle, which is suitable for the cases of low Tip Speed Ratio (TSR), is proposed; an actuator for collective pitch control is designed, which can change the blade pitch angle of multiple blades. A prototype is presented from the aspects of actuator of collective pitch control, airfoil selection, structure of wind wheel and control system. The performance tests of the prototype were carried out. The results show that the best thickness of the symmetrical airfoil is 15%, while the maximum thickness of asymmetrical airfoil is less than 10.4%. The theoretical data show similar variation trend but is 20%-30% higher than experimental data. The results also show that, to improve the self-starting toque, it is effective to increase the frontal area of the blade at downwind region of upstream.
立轴风力机具有结构简单、便于安装维护等优点[ 1],立轴风力发电技术已成为新能源开发利用的热点,然而启动能力差限制了该类风力机的推广[ 2]。为此,国内外学者对立轴风力机的启动性能展开研究并提出一些解决方法,其可以归纳为附加装置法、组合风轮法、改进翼型法和变桨距控制法。
附加装置法分为挡风装置[ 3]和导流叶片两种,文献[4-5]中利用导流叶片来改善启动性能后,风能利用率提高1.5倍。组合风轮也是一种改善启动特性的手段[ 6],且S型叶片与非对称翼型组合的效果更明显[ 7]。此外,研究表明,翼型厚度和弯度直接影响风力机的启动能力[ 8, 9, 10, 11];Baker[ 12]发现非对称翼型可以在较宽的攻角范围内改善风力机的启动特性;Selig等[ 13]指出:中等弯度可以改善启动特性,而大弯度翼型不会提高启动能力,反而会降低风能利用率;Dominy等[ 14]的研究表明:三叶片风力机可在任意方位下启动,而两叶片风力机在某些区域无法自启动。文献[15]提出定桨距立轴风力机不具有启动能力,故变桨距控制成为改善立轴风力机启动性能的又一研究热点[ 16]。
综上所述,附加装置法通过降低逆风区的阻力矩以增加净驱动力矩,但导致结构受力不均情况加剧;组合风轮虽然提高了低尖速比下的启动能力,但当风力机正常运行时S型叶片会影响直纹叶片的气动性能[ 17];改进翼型法增加了叶片制造的难度和成本,被动适应流场变化且受雷诺数影响严重。而变桨距控制不仅可以提高启动能力、实现最大功率跟随和功率控制,还可以降低叶片承受的动态载荷。故本文研究变桨距控制技术以改善立轴风力机的启动性能。根据立轴风力机的气动模型,提出了可以提高启动能力的桨距角变化规律;设计了变桨执行机构。实现了多组叶片的统一变桨距控制,并进行了样机性能实验。
立轴风力机的Darrieus运动使得其周围流场极其复杂,叶片气动性能受尾流干扰严重,导致作用在叶片上的气动力随方位角 θ的变化而时刻变化,如图1所示。叶片局部风速 Vθ和风轮切向速度 Uθ以及相对风速 Wθ的关系为:

由于攻角对叶片气动性能有直接影响,分析叶片攻角动态变化情况是设计桨距变化规律的前提,由图1可知,叶片攻角 αθ、来流角 γθ和桨距角 βθ的关系可以表示为:
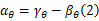
定义翼型的气动参数矢量 Cr:
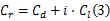
式中: Cl和 Cd分别为升力系数和阻力系数;i= 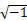
作用在单个叶片单位长度上的气动力为:
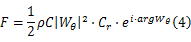
基于叶素理论,立轴风力机的瞬时功率为:
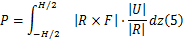
式中: ρ为空气密度; C为叶片弦长; H为叶片展长; R为叶片安装半径。
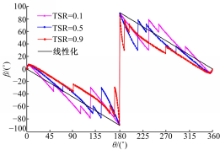
立轴风力机的瞬时功率是相对风速、瞬时攻角和方位角的函数,若风力机的结构参数和局部流场(来流风速和转速)已知,则通过改变桨距角可以实现瞬时功率的最大化。根据式(5)以立轴风力机的最大瞬时功率为目标函数编写Matlab M函数,得到了低尖速比下的桨距角变化规律,如图2所示。
由图2可知,一个运行周期内的桨距角变化规律关于方位角180°中心对称,且随着尖速比的增加,桨距角波动范围变小。尖速比小于1时的桨距角始终在图2中直线附近波动,且尖速比为0.5时的桨距角变化规律与直线吻合程度较好。为此对桨距角变化规律进行线性化处理,即将图中直线作为尖速比小于1时的桨距角变化规律,经线性化处理后桨距角 βθ与方位角 θ的关系为:
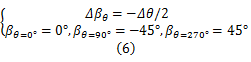
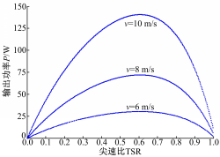
经过线性化处理后,各叶片的初始桨距角如式(6)所示,而叶片桨距角的变化量为风轮方位角变化量的1/2,叶片的旋转方向与风轮的旋转方向相反。为了验证经线性化处理后的桨距角变化规律的可靠性,本文进行了仿真验证,仿真结果如图3所示。
由图3可知,随着风速的提高,风力机输出功率增加,最大输出功率也明显提高。仿真结果还表明:在变桨距规律下,风力机的最佳工作尖速比为0.5~0.7,与线性化处理的结果基本一致,说明线性化处理是可行的。
由式(6)可知,经线性化处理后的桨距角变化率相同,故立轴风力机可以采用统一变桨距控制[ 18],即所有叶片由一个变桨执行机构驱动,叶片桨距角变化相同。文献[19]中也提出了一种基于式(6)中桨距角变化规律的立轴风力机,该样机由风向标提供桨距角驱动力矩,由于风向标必须与风向产生一定的偏角才能产生足够大的驱动力矩,且风向标的结构参数通常很大,导致叶片不能准确地跟随风向变化,是式(6)中桨距角变化规律的一种近似。
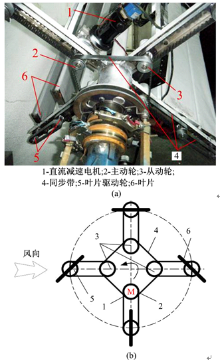
本文设计了一款可实现式(6)中桨距角变化规律的立轴风力机,由风向仪采集风向、直流减速电机提供驱动力矩以提高对风向的动态跟随特性;并提出了一种单输入多输出的变桨执行机构以实现多组叶片的统一变桨距控制,所设计的变桨执行机构如图4(a)所示,且各同步带轮的传动比关系为1∶1。
变桨执行机构的工作原理为:叶片安装时相差45°相位角,由一台直流减速电机驱动主动轮,经同步带将主动轮的旋转运动传递给另外3个从动同步带轮;主动轮和3个从动轮又分别将运动传递到叶片驱动轮,实现了四组叶片的桨距角调节。当风向发生变化时,根据风向仪采集的风向变化量,直流减速电机驱动叶片转动相应角度,始终保证叶片初始安装位姿正对风向,其示意图如图4(b)所示。
所设计的变桨执行机构由一台直流减速电机同时实现了多组叶片的统一变桨距控制,降低了变桨距控制的成本。与文献[19]中提出的立轴风力机相比,所设计的变桨距执行机构更加简单,提高了跟随风向变化的精度以及变桨距控制精度。
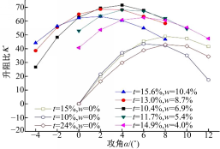
由式(4)可知,作用在叶片上的气动力取决于翼型的升阻力系数,翼型升阻比 κ( κ=Cl/Cd)对整体效率有很大影响。研究表明较高的升阻比可以在较宽的攻角范围内产生较大的切向力,所以选择合适的翼型可有效提高风力机的启动能力。图5为不同翼型的升阻比曲线,其中 t为相对厚度, w为相对弯度。
由图5可知,非对称翼型升阻比曲线的峰值远大于对称翼型的峰值,表明非对称翼型的启动性能要优于对称翼型。对称翼型在0°攻角下的升阻比为0,而非对称翼型的升阻比不为0;同时对称翼型获得升阻比峰值的攻角大于非对称翼型,表明在较小攻角下非对称翼型更容易发生动态失速。
由图5还发现:①对称翼型取得较高气动性能时的相对厚度为15%,而相对厚度过大不仅增加了叶片的质量,同时也会影响叶片的气动特性;②非对称翼型在 t=10.4%、 w=6.9%时获得升阻比峰值的最大值;而其他情况无论相对弯度增加与否,由于相对厚度增加,升阻比的峰值都降低,可以推断非对称翼型的最大相对厚度不能超过10.4%;③相比于升阻比峰值最大的情况,若相对弯度减小,升阻比峰值向大攻角方向移动,这是因为翼型相对弯度变小使得有效攻角变小,翼型只有在较大攻角下才能达到失速;若相对弯度变大,升阻比峰值向小攻角方向移动,这是由翼型弯度变大、有效攻角增大,翼型在较小攻角就达到失速导致的。
由于风轮旋转过程中,叶片攻角波动范围较大,选择对称翼型可以使叶片在较大的正攻角范围内工作,可提高风力机的风能利用率。而对于式(6)中的桨距角变化规律,若采用对称翼型(如NACA系列翼型),风轮旋转两周叶片才旋转一周,而在风轮第二个旋转周期内叶片的位姿(前缘在后,尾缘在前)不利于风能的获取。鉴于本文主要分析和验证统一变桨距规律及变桨距机构的可行性,所以样机安装平板翼型,平板翼型不仅使得叶片桨距角变化周期与风轮运行周期相等,而且加工制造方便,成本低。
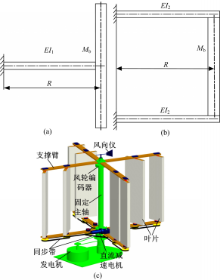
立轴风力机结构简单,但由于叶片支撑方式以及发电机安装的多样化,又呈现出不同的整体布局。叶片支撑方式对风轮结构起主导作用,单臂悬臂式和双臂简支式支撑是两种常见的支撑方式。支撑臂在叶片质量作用下发生弯曲变形,且受到流场的作用产生振动,由于叶片支撑的刚度和振动特性对直纹叶片的气动性能有较大影响,故研究由叶片和支撑臂组成的振动系统的特性是风力机结构设计的基础。如图6所示,支撑臂一端与主轴刚性连接,且视为固定端;另一端则与叶片采用可靠连接,叶片质量为 Mb,安装半径为 R。单、双臂两种支撑方式下支撑臂材质相同,单支撑臂的抗弯刚度为 EI1,双支撑方式下每个支撑臂的抗弯刚度为 EI2。
单臂悬臂式支撑方式下,自由端的挠度为:

单支撑臂与叶片组成系统的固有频率为:
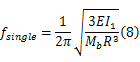
双臂简支式支撑方式下,自由端的挠度为:

则双臂简支式振动系统的固有频率为:

由式(7)~(10)可知:若单、双臂两种支撑方式的抗弯刚度相等,即 EI1 =EI2,则双臂支撑方式的自由端挠度比单臂支撑方式大大降低,且固有频率大大提高,降低了发生共振的可能性。即如果挠度相同,双臂支撑方式可以大大降低支撑臂质量并节约制造成本。故样机采用双臂简支式支撑形式,如图6(c)所示。
目前直驱技术成为立轴风力机发展的趋势,直驱式发电机不仅可以简化结构以提高传动效率,还可以更快地适应风载变化[ 2],但是该类发电机制造成本较高,故样机没有采用直驱技术,而是通过一级传动将风轮运动传递给发电机,如图6所示。
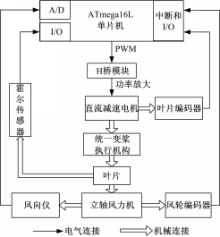
立轴风力机的统一变桨距控制系统框图如图7所示。控制系统主要由单片机、H桥模块、风向仪、风轮编码器、叶片编码器和霍尔传感器等组成。风力机发出的电能存储在24 V蓄电池中,同时蓄电池为单片机等控制系统供电。风力机运行前首先要建立风力机坐标系统:根据风向仪和风轮编码器输入的信息确定风轮旋转坐标系,用叶片编码器和霍尔传感器确定叶片坐标系。风向和风轮方位角是系统输入,分别经A/D模块、中断和I/O处理后传递给控制器;单片机输出PWM信号并通过H桥功率放大模块驱动直流电机,再经变桨执行机构调整叶片桨距角;直流电机尾部安装叶片编码器反馈叶片桨距角信息,从而实现叶片桨距角的位置闭环控制。
以ATmega16L单片机作为控制器,利用中断和I/O资源实现了叶片和风轮在各自坐标系统下的位置确定。每一个运行周期内风轮编码器输出一个脉冲Z信号,由向量等级最高的INT0来准确可靠地捕捉该信号。风轮方位角信息是系统的给定信号,该信号的准确性直接关系到整个系统的控制精度,故由向量等级次高的INT1来获得该信号。通过定时器Timer0溢出中断实现采样周期定时中断,而叶片桨距角信号的采集通过触发外部中断INT2计数确定。
实验样机的叶片安装半径为557 mm,叶片展长为1000 mm,每个支撑梁上可以安装1~2组叶片,叶片弦长分为350 mm和175 mm两种。样机实验主要研究不同风速下样机的发电功率,以验证统一变桨执行机构的可行性。此外,通过改变叶片弦长、支撑梁数目及其叶片安装数目等因素研究实度对立轴风力机启动能力的影响。
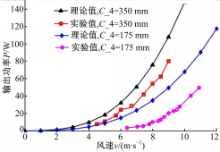
实验样机的发电功率曲线如图8所示。由图8可知,无论是实验数据还是理论计算数据,4个宽叶片( C=350 mm)的性能都远远优于4个窄叶片( C=175 mm),可见增大叶片弦长对提高立轴风力机的整体性能有一定帮助。此外,实验数据与理论值变化趋势一致,但是相比理论值偏低,实验值与理论值的偏差为20%~30%。这是因为气动模型是建立在叶素理论基础上的,没有考虑叶片动态失速、三维空间流场的影响,使得理论计算值偏大,这一点已经在文献[20]中得到验证。同时实验数据测量的是发电机的输出功率,没有考虑机械摩擦和发电机损耗等问题。基于以上原因,最终导致实验值与理论值存在一定的偏差,可见气动模型理论的完善对设计变桨距控制规律至关重要,不过实验结果足以说明所设计的变桨执行机构可实现预期的统一变桨距控制,图中的“ C_4”代表4宽叶片。
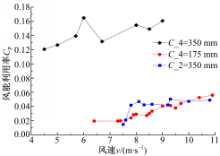
根据样机的输出功率,可得到实验样机在统一变桨距控制下的风能利用率曲线,如图9所示。由图9可知,随着风速的增加,风能利用率呈现上升趋势,且安装4宽叶片的情况下的风能利用率最高,平均风能利用率达到14.4%。对于风轮实度相同的两种情形( C_4=175 mm和 C_2=350 mm),样机的风能利用率基本相当;而对于2宽叶片情形,叶片间的相互干扰较小且流场受扰动情况较小,所以2宽叶片样机的平均风能利用率高于4窄叶片的情形。
样机的启动力矩曲线如图10所示。由图10可知,样机一个运行周期内输出力矩的周期数与支撑臂数目相同。支撑臂数目相同时,随着叶片弦长的增加,启动力矩也增加;叶片弦长相等时,支撑臂数量增多,风力机实度增大,启动力矩也增大。当风轮支撑臂为2时,在风轮支撑臂上安装两个叶片( C_2+2=175 mm+350 mm)的最大启动力矩高于安装一个叶片的情形( C_2=350 mm和 C_2=175 mm),可见增加上盘面顺风区叶片的迎风面积对提高样机的启动力矩很有帮助;而在上盘面逆风区,由于两个叶片间的干扰加剧,安装两个叶片情形下的风能利用率降低,启动力矩小于安装一个叶片的情形。对于 C_2=350 mm和 C_4=175 mm两种情形,风力机的实度相同,但4窄叶片的启动力矩远远大于2宽叶片的情形,可见增加叶片数量可以提高启动能力。
根据立轴风力机的气动模型获得了适宜低尖速比运行的桨距角变化规律,基于线性化的桨距角规律提出了一种变桨距执行机构以实现多组叶片的统一变桨距控制。所设计的变桨距执行机构结构简单,消除了机械式变桨距控制机构中风向标与风向的固有偏差,可提高风向动态跟随精度,且叶片桨距角可控性好。
研究结果表明:非对称翼型有助于提高立轴风力机的启动能力,但非对称翼型的最大厚度不得超过10.4%;对称翼型的厚度为15%时对启动特性的改善最为明显。实验结果表明:实验值与理论值一致性较好,设计的统一变桨距控制执行机构是可行的;但由于基于叶素理论建立的气动模型简化了流场环境,导致计算结果偏大,理论值与实验值存在20%~30%的偏差。研究还发现:适当增加叶片数量、弦长等实度因素以及增加上盘面顺风区的迎风面积,可以提高立轴风力机的启动能力。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|