作者简介:朱晓林(1983-),男,博士研究生.研究方向:地下换热结构热力耦合.E-mail:zxl_good2005@163.com
通过建立换热管典型平面弯曲态几何模型及本构模型分析不同温度地下换热管传热过程中管土结构热变形特征,着重研究典型初始弯曲管体热变形对管-土间隙演变发展的影响。研究表明,通常换热管弯曲凹侧出现较大间隙,其间隙分布占管体周边一半左右;当换热管初始弯曲较小或基本无弯曲时,其较大间隙出现在U形换热管的两管间对应区域,管-土间隙量随初始弯曲程度的增加而增加。
The geometrical model of typical plane bending state of heat exchange pipe and the constitutive model are established. Then the thermal deformation characteristics of pipe-soil structure in heat transfer at different temperatures are analyzed. It is focused on the influence of typical initial thermal deformation of bending pipe on the development of pipe-soil gap evolution. Results show that larger pipe-soil gap appears in the concave side of the bending heat exchange pip. The gap distribution around the buried pipe is about half of the pipe perimeter. The larger gap of smaller bending deflection or no bending heat exchange pipe mainly appears at the corresponding area between two pipes of U-type heat exchange pipe. The magnitude of pipe-soil gap increases with the bending degree of the heat exchange pipe.
季节性太阳能集热地下储能技术和地源热泵系统为建筑物提供清洁高效的能源,减轻建筑用能负荷的季节不均衡性[ 1],近年来也逐步应用于道路融冰化雪等领域[ 2]。地下换热管是地下蓄能及地源热泵系统中的关键部分,长期变化的温度载荷将导致换热管体产生热变形以及出现管-土间隙。
储热过程中换热管体随温度的升高发生热胀形变,挤压回填土产生一定的弹塑性变形,而在取热工况下回填土塑性变形部分不能完全伴随管体变形回弹,从而使管体与回填土间产生间隙,出现热阻增大的情况,降低换热能力,特别是中高温地下储热[ 3, 4, 5]再利用过程中,这种状况将进一步加剧并制约地下换热管长期应用的可靠性。
在国内外地下换热管的长期研究与应用过程中,研究人员更多关注地下换热管换热能力的不断提升,对于换热器管体热形变及围土结构强度失效等相关研究不多。德国Justus Liebig University大学的Sanner教授等[ 6]进行了90 ℃高温岩土储热研究工作,发现蓄能结构热形变和冷缩热胀问题,建议开展地下换热管热形变行为的相关研究。美国BNL国家实验室Allan等[ 7]也提出地下换热管和回填土热应力、热形变和承压特性等研究问题,并利用有限元软件ANSYS进行了换热体的热应力数值计算研究。Suryatriyastutia等[ 8]利用有限差分软件FLAC研究了地源热泵换热桩在静态热载荷条件下桩-土的力学行为。Philippacopoulos等[ 9]计算分析管-土间隙宽度为1.6 mm时,管-土间传热系数降低60%。
本文采用有限元软件ABAQUS针对换热器在地下蓄能及再利用过程中的管-土结构热形变进行数值计算分析,探究换热器管-土间隙的产生机理和分布特性,为提高地下换热管应用的可靠性提供理论依据。
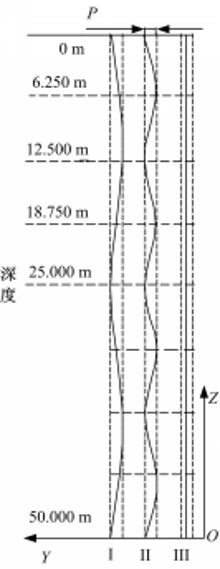
地下换热管安装施工过程中,由于受各种不确定因素的影响,地下换热管很容易出现弯曲,这种初始弯曲状态因施工条件等实际情况影响而具有随机性。为了便于计算分析,假设两种具有典型初始弯曲态的管体几何模型,分别为少弯的三弯曲和多弯的七弯曲管体模型Ⅰ、Ⅱ,最大弯曲挠度均为 P=0.1 m,模型Ⅲ为管体无弯曲理想模型,深度方向总长为50 m,如图1所示。
建立的模型基于以下假设:①换热管的初始弯曲为平面弯曲;②认为管体轴向温度均匀分布;③材料物性各向同性,回填土与围土的物理性质相近;④忽略初始应力、渗流及孔隙水对应力、应变和温度的影响。
管体及回填土热形变弹性部分计算基于热弹性力学模型,根据线性热应力理论,物体内部微元体总应变由应力和温度变化共同作用产生,从而把基于广义虎克定律的弹性模型推广到包括热应力与应变在内[ 10]的弹性模型;回填土及周围土壤热形变中的塑性形变部分采用摩尔库伦(Mohr-Coulomb)模型[ 11]计算。结构热形变过程中,换热管与回填土之间存在高度非线性的复杂接触行为,需要添加接触单元[ 12],接触单元力学模型采用各向同性的扩展库伦摩擦模型,建立接触面上的剪切应力与法向应力函数关系[ 13]。
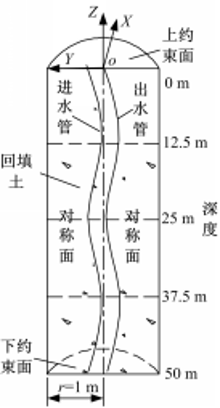
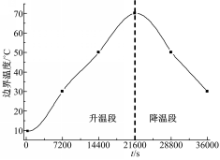
由于几何对称性,取模型一半结构用于计算,计算域半径为1 m,如图2所示。管体外径为0.032 m,壁厚为3.5 mm,钻孔直径为0.2 m,管中心间距为0.08 m。温度场计算中模型初始温度为10℃,管体内壁温度随时间变化,分为升温和降温两个阶段,如图3所示。形变位移计算中,换热管与围土间采用罚函数摩擦算法,摩擦因数为0.1,法向接触形式采用“硬接触”[ 14];模型的对称面施加 X方向对称约束条件(XSYMM),顶、底面为完全固定约束,其他外侧面施加 X、 Y方向固定位移约束,以防止模型在任意方向上的刚体运动,确保计算不会产生数值奇异。采用六面体三维网格单元离散化几何模型,分别设置网格单元属性DC3D8及C3D8R用于温度场及位移场计算。Ⅰ、Ⅱ、Ⅲ三种结构模型的网格单元总个数分别为112 000、119 500、110 000,轴向分布500个网格节点,在靠近换热管附近区域加密网格,以增加单元数量来提高接触面附近区域参数的计算精度。
首先用ABAQUS传热计算模块进行非稳态热传导数值计算,然后将温度场分布计算结果作为边界条件,输入到模型形变位移计算中进行热力耦合计算;有限元动态显式算法(ABAQUS/Explicit)可以模拟接触条件和其他不连续情况,且不需要迭代和收敛准则,能够有效计算结构形变过程中管体与回填土接触面间复杂的接触关系,所以采用有限元动态显式算法进行模型的热形变位移计算,该计算方法的有效性已经在文献[15]中得到了实验验证。
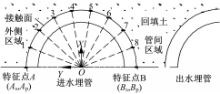
首先以进水管体为分析对象,分别取模型Ⅰ、Ⅱ中25 m、18.75 m深度横断面为特征面1、2和特征面1'、2',模型Ⅲ中取25 m深度横断面为特征面3。利用回填土接触面特征点 As、 Bs及管接触面特征点 Ap、 Bp相对于初始态的径向位移(相对位移),表征模型在温变工况下热形变历程及轴向间隙分布特性;特征点 A-1 -8 -B表征特征面径向间隙分布,如图4所示。
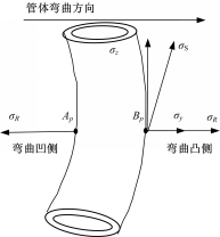
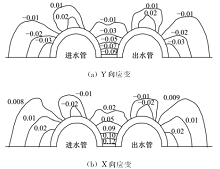
在升温段(储热工况),热膨胀形变、固定边界和回填土的约束作用使管体产生轴向、径向的热应力。由图5可知,管体的径向热应力由轴向热应力 σS的径向分力 σy与管体径向热应力 σR的合力构成,共同挤压回填土出现弹塑性应变,管间区域回填土同时受到进、出水管形变的挤压和剪切作用,导致此区域回填土 Y、 X向塑性应变呈负、正值,且绝对值大于其他区域,以特征面1塑性应变分布为例,如图6所示。
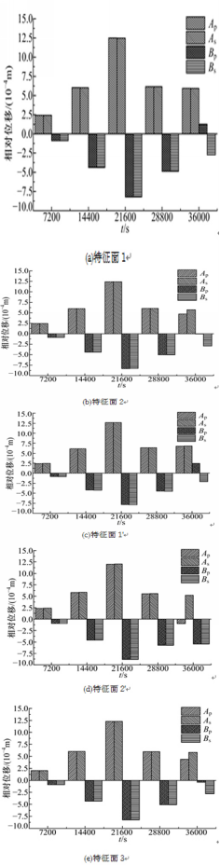
由图7可知,随着边界温度的不断升高, A、 B特征点的相对位移持续增加, As与 Ap、 Bs与 Bp的相对位移值一致,管体和回填土在升温过程中保持接触状态。事实上,由于钻孔尺寸的限制,管体最大弯曲挠度较小,导致 σy相对于 σR为一个微小值,所以管体径向膨胀形变占主要地位。两种模型与理想模型(模型Ⅲ)相比较,其特征点相对位移值趋于一致。在第7200、14 400、21 600 s时, A特征点相对位移量分别是 B特征点相对位移量的2 .87、1 .45、1 .61倍,这是由于特征点 B位于管间区域,其 Y轴负方向的形变位移受到出水管体 Y轴正方向热形变位移的抑制作用,随着温度的升高,抑制作用整体呈减弱趋势。
在降温段(取热工况),特征点相对位移减小。降温段中期(28 800 s),位于管间区域的特征点 B相对位移值较升温段中期(14 400 s)减小,说明管间区域回填土热形变回弹能力减弱。降温段末期,不同模型管-土特征点的径向相对位移出现差异,其差值即为间隙宽度值,简称间隙值。
特征面1处于管体 Y正向弯曲最大挠度位置。由图7(a)可知,管体弯曲凸侧的特征点 Ap、 As相对位移几乎无差异,而弯曲凹侧特征点 Bp与 Bs的相对位移方向相反,表明 Bs未能跟随 Bp回弹而导致管与回填土接触面分离,在管体弯曲凹侧出现值为4.0×10-4m的间隙。这是由于管体径向热应力大幅减小使其迅速回弹,而管体轴向尺度远大于径向,轴向残留较大的热应力,在这种情况下 σy相对于 σR不再是一个微小值。在管体自身径向回弹形变的同时, σy促使管体沿弯曲方向继续移动,含有塑性应变的回填土未能跟随管体回弹,从而导致管体弯曲凹侧出现较大间隙。特征面2位于管体弯曲挠度较小的位置,其特征点相对位移状态与理想模型接近,如图7(b)(e)所示,弯曲凹侧特征点间隙值为2.9×10-4m,小于特征面1弯曲凹侧的特征点间隙值,相应的弯曲凸侧特征点仍然存在1.0×10-4m的间隙,说明弯曲挠度越小的位置 σy越弱,即管体弯曲凸侧向管体弯曲方向形变位移的能力越差。
特征面1'、2'分别位于管体 Y轴正、负向弯曲最大挠度位置,由图7(c)(d)可知,随管体弯曲方向的不同, Bp、 Ap特征点均明显出现与 Bs、 As相反方向的相对位移,分别在特征面1'、2'中管体弯曲凹侧特征点出现5.8×10-4m、6.1×10-4m的间隙,均大于特征面1、2中的特征点间隙值,这说明同一钻孔中相同最大弯曲挠度的管体弯曲段越多,管体弯曲凹侧的间隙越大。
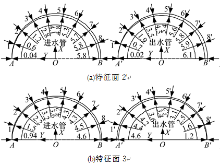
以特征面2'、3的间隙分布为例进行分析,限于篇幅其他模型特征面间隙分布未列出。由图8(a)可知,对于 Y正向弯曲的管体,沿特征点 A-1 -8 -B、 A'-1 '-8 '-B'间隙值呈现递增趋势,分布在进、出水管体弯曲凹侧的特征点4 -B、4 -B'间隙值大于平均值(3.6×10-4m、3.9×10-4m),在约占1/2管体周长范围内分布,出水管间隙值整体大于进水管间隙值,特征面1'间隙分布规律与之相反。对于特征面3,间隙值沿特征点 A-1 -8 -B、 B'-8 '-1 '-A'呈现递增趋势,进、出水管体大于平均间隙值(3.4×10-4m、3.1×10-4m)的特征点分布范围主要集中在管间区域,如图8(b)所示。
(1)钻孔尺寸的限制使换热器管体处于小弯曲挠度状态,升温过程中弯曲态管体轴向热应力的径向分力远小于径向热应力,其热变形主要表现为管体的径向热膨胀,挤压回填土产生弹塑性变形,不同初始弯曲态管体的变形位移量趋于一致。
(2)进、出水换热管间的回填土受两管体热变形的共同挤压和剪切作用,其塑性变形程度较其他区域严重,大大弱化了其回弹变形能力,此区域极易出现间隙。
(3)在降温过程中,换热管发生径向回弹变形,管体轴向残留热应力的径向分力作用逐渐凸显,促使管体继续沿弯曲方向变形,导致管体弯曲凹侧出现较大间隙(大于间隙平均值),管-土间隙量随初始弯曲程度的增加而增加。
(4)管体弯曲凹侧通常出现较大间隙,间隙分布占管体周边一半左右区域;弯曲挠度较小或无弯曲管体的较大间隙主要集中在两管间对应区域。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|