作者简介:王继利(1987-), 男,博士研究生.研究方向:数控机床可靠性.E-mail:wangjili1100@126.com
以两参数威布尔分布为多重威布尔混合模型的基函数,建立了以极大似然函数为目标的参数估计优化模型,并改进了求解优化模型的EM算法。改进EM算法中提出贝叶斯随机分类方法,用于初始化算法中的待估计参数。采用径向基函数插值法求解EM算法极大化步中的超越方程组,并通过实际算例对比分析了改进EM算法与传统算法的准确性。给出了用改进EM算法求解多重威布尔混合模型参数的具体算例,分析了多重威布尔混合模型的逼近性能。针对国内同期出厂的10台某型号冲压机床,通过现场跟踪获取其初期故障样本数据,运用多重威布尔混合模型研究可靠性数据分布规律,并研究了KS检验统计量
Taking two-parameter Weibull distribution as the basis function, an optimization model is established based on the maximum likelihood method for parameter estimation, and the model is solved by improved Expectation-Maximization (EM) algorithm. Bayesian random classification algorithm, which is used for parameter initialization, is proposed in the improved EM algorithm. Radial basis function interpolation is used to solve the transcendental equation in the maximization step of the EM algorithm. The performance of the improved EM algorithm is compared with traditional algorithms by case study. Approximation performance of finite Weibull mixture distributions is analyzed with specific cases. The distribution law of the reliability data of ten punching machine tools, which come from testing field, is investigated by Weibull mixture distributions. The relationship between KS test statistic and the number of Weibull distributions is analyzed. The case study suggests that the fourfold Weibull mixture distributions could be better reflect the real law of the punching machine tools in early stage.
(College of Mechanical Science and Engineering,Jilin University,Changchun 130022,China)
Abstract:Taking two-parameter Weibull distribution as the basis function, an optimization model is established based on the maximum likelihood method for parameter estimation, and the model is solved by improved Expectation-Maximization (EM) algorithm. Bayesian random classification algorithm, which is used for parameter initialization, is proposed in the improved EM algorithm. Radial basis function interpolation is used to solve the transcendental equation in the maximization step of the EM algorithm. The performance of the improved EM algorithm is compared with traditional algorithms by case study. Approximation performance of finite Weibull mixture distributions is analyzed with specific cases. The distribution law of the reliability data of ten punching machine tools, which come from testing field, is investigated by Weibull mixture distributions. The relationship between KS test statistic and the number of Weibull distributions is analyzed. The case study suggests that the fourfold Weibull mixture distributions could be better reflect the real law of the punching machine tools in early stage.
Key words:machinery manufacturing automation;reliability of machine tools; finite Weibull mixture distributions; maximum likelihood method; EM algorithm; Bayesian random classification; radial basis function interpolation; KS test
目前,常用的可靠性建模理论主要包括两类:一类是基于故障间隔时间数据建模的黑箱理论,该理论普遍采用简单分布进行可靠性建模,如正态分布、指数分布、威布尔分布模型等[ 1, 2, 3]。另一类是针对基于系统状态的随机过程理论,最典型的建模方法是马尔可夫过程。但两种可靠性建模理论都存在一定缺陷,黑箱理论中的简单分布模型只能近似建模故障数据,由于数控机床属于复杂可修系统,系统故障通常是由多种失效模式所致[ 4, 5],简单分布模型建模方法难以保证故障数据建模的准确性。而随机过程理论需要有严格的条件约束[ 6, 7, 8],即系统的各部件寿命分布和故障后修理时间分布及其他分布均为指数分布时,适当定义系统状态,系统才可以用马尔可夫过程描述。一旦离开指数分布的假定,随机过程建模方法往往会变得困难。
针对基于黑箱理论的可靠性建模方法,本文采用多重威布尔混合模型替代传统的简单分布模型。目前,最常见的威布尔混合模型是两重混合[ 9, 10, 11]。由于三重以上的混合模型卷入参数较多,导致参数估计困难,多重威布尔混合模型应用很少。本文根据极大似然函数法建立参数估计的最优化模型,基于贝叶斯分类思想提出一种随机分类方法,通过改进传统EM算法[ 12]得到一种多重威布尔混合模型的参数估计方法。并将本文方法应用于国内某型号冲压机床早期的可靠性建模。
在许多情况下,一个总体可能由两个或多个子体组成。例如,由于设计、原材料、制造工艺等方面的差异,在不同情况下生产的产品可能有不同的寿命分布。如果一个总体由 n个子体组成,对应的子体的累积分布函数和混合比例(或混合权)分别是 F1( x), F2( x),…, Fn( x),以及 ω1, ω2,…, ωn,则总体的累积分布函数是:
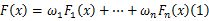
相应的混合模型密度分布函数为:
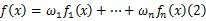
式(1)是混合模型的一般形式,称为 n重威布尔混合模型。其中 n重是指 n个两两不完全相同的子体混合。混合权 ω1, ω2,…, ωn满足: 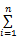
如果 Fi( x)是两参数或三参数威布尔分布,分别是:
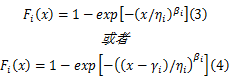
采用传统的参数估计方法,如矩估计、极大似然估计等估计多重威布尔混合模型的参数比较困难。矩估计需要根据待估计参数个数列出矩估计方程组,极大似然估计需要根据极大似然函数列出似然方程组,二者都是超越方程组。多重威布尔混合模型自身解析式复杂,矩估计法、最大似然估计法求解过于繁杂,难以实现参数的准确估计。为了回避传统参数估计方法的复杂过程,降低多重威布尔混合模型参数估计难度,选用两参数威布尔分布作为基函数,根据极大似然函数建立多重威布尔混合模型参数估计的优化模型:
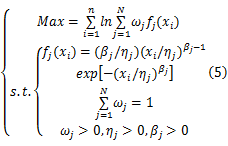
式中: ηj为第 j个威布尔分布的尺度参数; βj为第 j个威布尔分布的形状参数; ωj为第 j个威布尔分布的权重系数; n为样本数据的个数; N为混合威布尔模型重数; xi为第 i个样本量的取值。
多重威布尔混合模型的待估计参数为 ηj、 βj、 ωj。参数个数取决于混合模型的重数 N,参数个数越多,参数估计难度越大。 EM算法是求参数极大似然估计的一种方法,它可以从非完整数据集中对参数进行最大似然估计,是一种非常简单实用的学习算法。
传统EM算法采用随机选取或经验选取的方法初始化待估计参数,容易造成迭代算法陷入局部最优。相关文献中采用绝对分类的初始化方法,如Kmeans分类、Binning分类。混合模型实际分布一般为多个独立分布的叠加,各独立分布之间存在交集,采用绝对分类初始化与理论情况不一致。本文提出一种贝叶斯随机分类的方法将不完全数据集随机分配到各独立分布,作为EM算法的初始化方法。贝叶斯随机分类方法步骤如下:
Step1 采用Kmeans聚类分析法对不完整数据集进行分类,对每类数据进行威布尔分布参数的极大似然估计,作为各独立分布的先验分布参数,第 j类样本数据对应的分布参数为( ηj, βj)。每类样本数据容量 gi占总容量 G的比值为各独立分布的权值 wi,即 wi=gi/G。
Step2 计算第 i点在第 j类独立分布的密度函数值 fij( xi),并根据式(6)归一化处理得到 pij, pij表示第 i个点隶属于第 j个独立分布的后验概率:
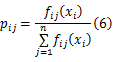
Step3 将第 i点分配到第 j类的后验概率区间为 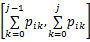
Step4 根据式(7)计算最大似然函数值,选似然函数值较大者为当前最优分类:
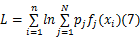
Step5 重复Step2~Step4,直到最大似然函数值收敛或迭代次数结束。
EM算法的核心思想是:根据已有的数据,借助隐藏变量,通过期望值之间的迭代,估计似然函数。具体EM算法步骤如下:
Step1 初始化参数 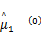
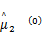

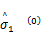
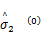
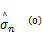



Step2 期望步。根据式(8)迭代计算响应度 γi:
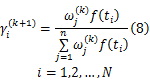
Step3 极大化步。根据方程式(9)迭代计算加权均值和方差:
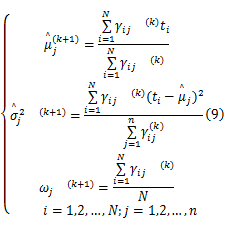
Step4 重复步骤Step2、Step3直到极大似然函数值收敛。
在Step3中, 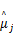

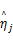
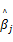
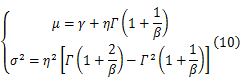
在EM算法中,每一次迭代都要求解方程(10),令 λ=μ/σ,当 γ=0时,则有公式:
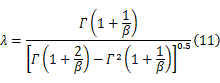
λ与 β显然存在单调关系,由于函数关系复杂,采用径向基函数插值的数值方法[ 13]根据 λ求解 β。然后,根据式(12)求解 η:
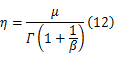
为验证参数估计方法的准确性,采用逆变换分布函数的方法产生多重混合威布尔分布的样本数据。根据逆变换得 x=F-1( y),其中 y服从(0,1)上的均匀分布。产生一组随机数 Y=[ y1, y2,…, yn],根据逆变换表达式得到服从多重混合威布尔分布的样本数据 X=[ x1, x2,…, xn]。给出不同重数的威布尔混合模型算例,分别产生容量大小为1000的随机样本,对比多重威布尔混合模型参数估计的常用方法,如传统EM算法、优化算法,给出实际算例的计算结果,如表1所示。
对比不同重数的混合威布尔分布算例,对比极大似然函数值 Lmax,可以看出,在威布尔重数为2的情况下,各种算法与理论分布都比较接近,估计结果无明显差异。威布尔重数大于3的情况下,改进的EM算法的参数估计结果更接近理论分布。
| 表1 不同算法对比参数估计值表 Table 1 Estimated parameters obtained by different methods |
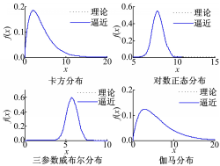
威布尔混合模型分布密度函数形状多样,当形状参数为1时,代表指数分布;当形状参数为2时,代表瑞利分布;当形状参数为3时,与正态分布极为接近。可以考虑用多重威布尔混合分布逼近其他分布,如三参数威布尔分布、 Γ分布、对数正态分布等。建立多重威布尔分布逼近其他分布的最小二乘拟合模型:
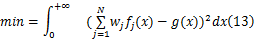
式中: 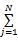
采用4重威布尔分布分别逼近三参数威布尔分布、 Γ分布、对数正态分布、 χ2分布。逼近效果如图1所示,4重威布尔分布与所逼近的分布几乎完全重合,说明多重威布尔混合模型具有良好的逼近性能。
以国内某机床厂同一时期出厂的10台某型号冲压机床为考察对象,研究机床初期故障数据分布规律。通过现场试验得到各台机床故障间隔时间如表2所示。
| 表2 冲压机床故障间隔时间数据表 Table 2 Failure data of punching machine tools |
采用传统的极大似然估计方法计算得到单重威布尔分布参数估计值,采用改进EM算法计算得到多重威布尔混合模型的参数估计值。参数取值如表3所示。
根据图2中不同重数的威布尔分布密度函数曲线,可以看出,随着威布尔混合模型重数的增加,数据分布规律趋于稳定。其中,4重与5重威布尔混合模型几乎重合,说明案例中的冲压机床可靠性分布规律在选用4重威布尔混合模型时达到稳定,更能反映该型号冲压机床早期可靠性的实际分布规律。
| 表3 多重威布尔混合模型参数表 Table 3 Estimated parameters of finite Weibull mixture distributions |
拟合优度检验是检验来自总体中的一类数据的分布是否与某种理论分布相一致的统计方法。常用的检验法有 t检验、 χ2检验、KS检验。其中, t检验属于正态性检验方法,不适用于其他分布的检验。 χ2检验与KS检验相比,KS检验具有适用于小样本、检验结果的鲁棒性强等特点。因此,本文选用KS检验方法。
若 Sn( x)表示一个 n次观察的随机样本观察值的累积概率分布函数, Sn( x) =i/n, i是等于或小于 x的所有观察结果的数目, i=1,2,…, n。 F0( x)表示一个特定的累积概率分布函数,也就是说,对于任一 x值, F0( x)代表小于或等于 x值预期结果所占的比例。于是定义 Sn( x)与 F0( x)之差的绝对值为 D,即:
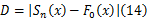
式中: Sn( x)为经验分布函数; F0( x)为理论分布函数,若对每一个 x值来说, Sn( x)与 F0( x)差异很小,则表明经验分布函数与理论分布函数的拟合程度很高,认为样本数据来自具有该理论分布的总体。KS检验集中考察统计量 Dmax,即:
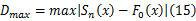
KS检验步骤中,首先建立假设:
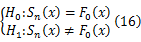
然后,计算统计量 Dmax。根据给定的显著性水平 α,样本个数 n,查单样本KS检验统计量表得临界值 dα。若 Dmax< dα,则在 α水平上,接受 H0;否则,拒绝 H0。根据该检验法得到混合威布尔分布模型重数 N对应的检验统计量 Dmax为0 .0756( N=1)、0 .0457( N=2)、0 .0225( N=3)、0 .0278( N=4)、0 .0276( N=5)。
查单样本KS检验统计量表得显著性水平 α=0.05对应的临界值 d0.05=0.2270。根据 Dmax值,在显著性水平 α=0.05时,威布尔混合模型重数为1到5的情况下,原假设 H0均被接受。并且,随着威布尔混合模型重数的递增,检验统计量 Dmax呈递减趋势,说明威布尔混合模型重数越高,分布模型的拟合优度越好。
(1)改进了传统混合威布尔模型参数估计算法,采用本文提出的贝叶斯随机分类算法作为EM算法参数初始化方法,并根据威布尔分布形状参数 β与统计量 λ之间的单调关系,采用径向基函数插值的数值方法求解EM算法中的超越方程组。改进算法简化了混合威布尔模型参数估计算法,能够提高算法收敛性能。
(2)混合威布尔模型具有良好的逼近性能,通过实例分析,说明了多重混合威布尔模型可逼近简单分布,如三参数威布尔分布、 Γ分布、对数正态分布。以某型号冲压机床的故障间隔时间为分析样本,结果表明4重威布尔模型能够准确反映冲压机床早期的可靠性分布规律。
(3)针对文中的冲压机床应用案例,分析了KS检验统计量 Dmax与混合威布尔模型重数 N之间的关系, Dmax随 N的增大呈现单调递减趋势,说明混合威布尔模型重数越大,样本数据的拟合优度越好。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|