作者简介:高印寒(1951-),男,教授,博士生导师.研究方向:车辆测试技术及仪器.E-mail:yinhan@jlu.edu.cn
利用一阶偏微分方程组将属于一阶双曲型偏微分方程组的多导体传输线方程变换为一阶线性常系数方程组,应用偏微分方程的特征线构造该方程组的一阶迎风格式,将一阶线性方程组的系数矩阵进行通量分裂,结合阻性负载的边界条件,计算出传输线的瞬态响应。最后通过仿真将本文计算结果与利用具有二阶精度的传统时域有限差分(FDTD)格式和Lax-Wendroff格式计算出的结果进行比较。结果表明:本文算法克服了传统FDTD格式和Lax-Wendroff格式在间断解处的非物理振荡,同时还具有简单稳定,适用范围广的特点。
Multi-conductor transmission line equations belong to the first order hyperbolic partial differential equations, which are converted into first-order linear constant coefficient equations by means of the first-order partial differential equations. It applies the characteristic line of the partial differential equations to construct its first-order upwind scheme, conducts a flux splitting of the coefficient matrix of the linear equations and combines the boundary conditions of resistive load to calculate the transient response of the transmission line. Finally, by simulation, the calculation results of this work are compared with that of the traditional PDTD format and Lax-Wendroff format with second order accuracy. It is demonstrated that the proposed calculation method overcomes the non-physical oscillation of traditional PDTD format and Lax-Wndroff format at the discontinuous solutions. At the same time the new method has the characteristics of simple and stable, wide range of application and similar efficiency to those two calculation methods.
由于电路集成度和数字信号的频率随着电气电子设备的迅速发展而不断地提高,这使得由互电感和互电容等因素引起的线束串扰问题变得越来越突出[ 1, 2, 3],而线束串扰会严重影响信号的完整性和可靠性,甚至可能损坏电路元件及误触发信号导致系统不能正常工作[ 1, 2, 3]。多导体传输线方程的本质是双曲型偏微分方程组,所以近年来偏微分方程的数值解理论已经成为了研究传输线瞬态响应的重要手段,并且取得了很好的效果,例如传统的FDTD格式[ 4],Lax-Friedrichs格式[ 5, 6],Lax-Wendroff格式[ 7],Upwind格式[ 8, 9]等。其中传统的FDTD格式与Lax-Wendroff格式是具有二阶精度的差分方法,虽然间断的过渡区域较窄,但间断前后有相对较大的非物理振荡,不利于提取完整的信号信息。文献[8]中的Upwind格式是将一阶拟线性方程组的差分格式用于计算传输线方程的数值解,但是其只能用于求解双导体传输线方程,而且在编程之前要进行复杂的计算和差分变换,步骤较为繁琐。本文将通量分裂法[ 10]应用于一阶迎风差分格式,将传输线方程的系数矩阵进行通量分裂,从而减小了推导过程的工作量,便于编程,同时还能够解决多导体传输线的串扰问题,扩大了其应用范围。
为了验证方法的有效性,通过仿真实验,将本文算法运行的结果和传统的FDTD格式及Lax-Wendroff格式求解多导体传输线串扰问题的结果进行对比。仿真结果表明,本文算法运算结果与FDTD及Lax-Wendroff算法运行结果基本吻合,并且克服了间断解处的振荡,更好地反应了串扰信号所包含的信息。
通量分裂也称特征分解,首先求出偏微分方程系数矩阵的相似对角矩阵,然后根据相似对角矩阵特征值的正负情况,将其表示为两个对角矩阵的和,其中一个对角矩阵的主对角线上的值由相似对角矩阵主对角线上正或者零的元素组成,另一个对角矩阵的主对角线上的值由相似对角矩阵主对角线上负或者零的元素组成。将通量分裂应用到如下形式的方程:

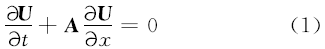
式中: U是含有 m个元素的列向量; A是 m×m的系数矩阵。
系数矩阵 A的相似变换过程可以表示为:
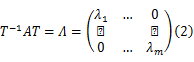
式中: Λ是系数矩阵 A的相似对角矩阵。
应用式(2)可以将式(1)表示为如下解耦方程:

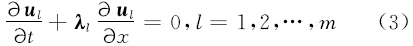
系数矩阵 A对应的相似对角矩阵中,任何的特征值 λl都可以表示为:
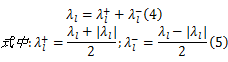
如果 λl≥0,则 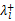
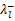
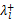
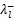
应用式(2)(5),可以分裂相似对角矩阵:
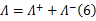
式中: Λ+和 Λ-分别有对角元素 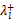
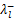
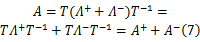
由上述可知,通量分解就是先对一阶线性偏微分方程组的系数矩阵 A进行相似变换,求得其相似对角矩阵 Λ,然后再将 Λ按照主对角线上特征值的正负进行分裂,得到 Λ+和 Λ-,接着将 Λ+和 Λ-相似对角化得到 A+和 A-。求得这两个矩阵对于利用一阶迎风格式求解传输线方程至关重要,因为一阶迎风格式的构建求解需要根据特征值的正负来选择向前差分还是向后差分计算。
多导体传输线的方程可以表示为:

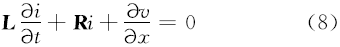
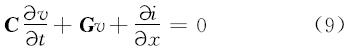
式中: R是传输线的分布电阻矩阵; L是传输线的分布电感矩阵; C是传输线的分布电容矩阵; G是传输线的分布电导矩阵。
为了推导出应用通量分解法的一阶迎风格式,将多导体传输线方程(8)(9)写成:

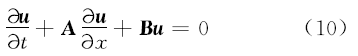
式中: u= 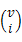

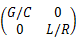
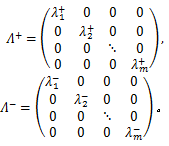
为了计算方便,此处引进一个新的特征变量:
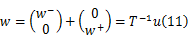
通过变换获得式(12):
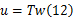
式中: T-1和 T为使系数矩阵 A对角化的可逆矩阵。
将式(11)(12)代入式(10)中可得用于推导边界条件的方程:

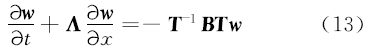
同时为了有利于应用一阶迎风格式,将式(10)表示为通量分解后的偏微分方程形式:

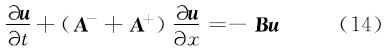
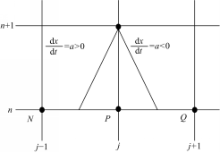
如图1所示,一阶迎风的差分格式是基于特征线的方向来确定插值区间,即对于 a>0,使用 N、 P两点进行插值,也就是向后差分;对于 a<0,使用 P、 Q两点进行插值,也就是向前差分。传输线方程式(14)是通过矩阵 A+和 A-的特征值来确定其特征线的方向的,其中 A+是向后差分, A-是向前差分,损耗项 Bu= 
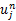
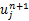
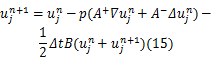
式中: Ñ和 Δ分别为表示向后和向前空间差分的标识符,通过将上式中空间标识符展开重新整理可得如下的显式格式:
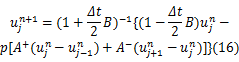
为了保证本文差分格式在计算中的稳定性,必须满足稳定条件,即 p≤ 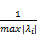
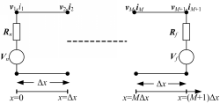
这里讨论传输线具有阻性负载的情况,多导体传输线空间离散方法如图2所示。由基尔霍夫电压定律和欧姆定律可得传输线源端和负载端的边界条件为:
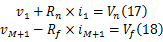
式中: Rn代表源电阻矩阵; Rf代表负载电阻矩阵。
应用式(13)可以将式(17)写成如下形式:
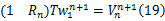
式中: 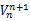
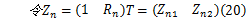
式中: Zn1和 Zn2分别表示 M×M的矩阵,则式(19)可以表示为如下形式:
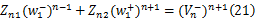
由稳定条件可得如下关系:
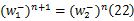
进而可以推得:
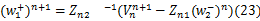
特征向量( 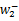
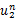
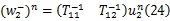
式中: 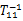
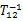
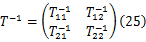
由式(12)和式(23)可获得源端的边界条件:
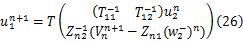
同样,负载端的边界条件可以表示为:
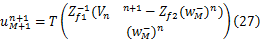
式中:( 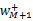
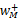
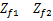
一阶迎风格式的多导体传输线内部各点的电压和电流可通过式(16)进行迭代,而源端和负载端的电压和电流通过式(26)(27)获得。
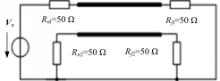
对图3中的(2+1)多导体传输线系统进行仿真。通过实例说明本文算法在传输线瞬态响应中的应用,并将计算结果与其他差分方法所得的结果进行比较。
假设多导体传输线的长度为1 m,它的单位长度参数矩阵分别为:
L= 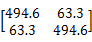
C= 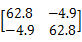
R= 
G= 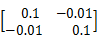
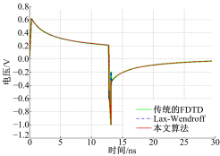
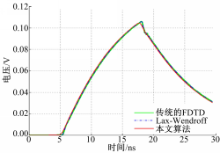
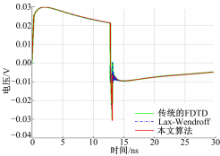
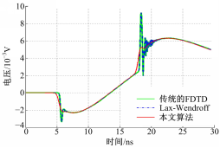
传输线的激励源为梯形电压波,上升和下降时间都为0.334 ns,顶部持续时间为12.5 ns,持续阶段的电压值为1 V。将传输线等分为200段,每段的长度(即空间步长)Δ x=0.005 m,传输线的源阻抗与负载阻抗都为50 Ω,对于本文算法和另外两种格式的算法均取空间步长Δ x=0.005 m,时间步长Δ t=(6e-12) s。发射线与受扰线的近端与远端电压计算结果如图4~图7所示。
从图4~图7可以看出,本文算法和传统的FDTD格式及Lax-Wendroff格式所仿真出的结果很吻合,在间断解处,本文算法的过渡区域与传统的FDTD格式及Lax-Wendroff格式的宽度基本一致;同时在时间步长及空间步长相同的情况下,3种格式的仿真效率也大致相同,但本文算法克服了传统FDTD格式和Lax-Wendroff格式在间断解处的较大的非物理振荡。
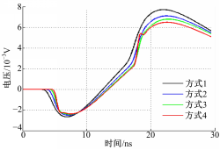
观察表1和图8可以发现,时间步长与空间步长减小,计算精度提高,但计算时间变长。因此在实际应用中,要综合考虑时间成本和计算精度,合理选择时间步长与空间步长。
| 表1 不同时间步长、空间步长的运行时间 Table 1 Running time of different time steps and different space steps |
根据传输线方程的双曲特性,结合通量分裂法,给出了可应用于传输线瞬态分析的具有一阶精度的迎风格式的差分方案。仿真结果表明:这种基于传输线方程时-空离散的数值计算方法不仅消除了因空间坐标离散而导致的间断解处的寄生振荡,而且克服了文献[8-9]只能求双导体传输线的限制,其边界条件表达更为简单,省去了复杂的数学推导,编程方便,可用于求解多导体传输线的方程。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|