作者简介:牛晓霞(1982-),女,博士研究生.研究方向:可重构编译,软硬件划分.E-mail:niuxiaoxia25@hrbeu.edu.cn
提出了一种改进的遗传算法,该算法在求解划分问题的同时也解决了多种硬件方式探索问题。算法依据硬件实现方式的硬件延时-面积矛盾的特征,结合Q-学习算法和贪婪规则,自适应地选择合适变异方向,减少变异盲目性,增强遗传算法的局部搜索能力。实验结果表明,与BUB算法和标准遗传算法相比,本文方法在搜索质量、收敛性方面具有更好的效果。
An improved genetic algorithm is proposed, which can solve the partitioning problem and the hardware implementation exploration simultaneously. In accordance with the characteristic of hardware delay-area contradiction in implementation, the mutation operator is chosen adaptively based on the Q-learning algorithm and greedy algorithm. The objectives are to avoid the blindness in mutation and to enhance the capability of local search of the genetic algorithm. Experiment results show that the improved genetic algorithm is more efficient than the greedy algorithm and the standard genetic algorithm in terms of searching quality and convergence.
基于FPGA(Field-programmable gate array)的可重构混合计算系统主要由通用处理器GPP(General purpose processor)和可重构加速单元RAUs(Reconfigurable acceleration units)两部分构成,其中,FPGA的可扩展、高速并行等特性为高性能计算提供了硬件支持,GPP的灵活性则为高性能计算提供了软件支持。为了使两种运算部件都能够发挥各自优势,设计人员需要通过软硬件划分方法,将应用程序所需完成的功能有效地分配到两个运算部件上。因此研究面向基于FPGA的可重构混合系统的软硬件划分方法对于充分发挥可重构混合系统的结构优势、构建灵活高效的可重构混合系统十分重要。
自20世纪90年代初CODES研讨会针对软硬件划分问题,首次提出“模型+算法”[ 1]的解决方案后,人们研究了各具特色的划分模型和划分算法,其中最常用的划分模型是任务图,划分算法有遗传算法[ 2, 3]、模拟退火算法[ 4]、禁忌搜索算法[ 5]等。已有划分方法通常默认应用程序在硬件处理器上只有一种实现方式,实际上一段应用程序可能存在多种硬件实现方式,这种多样性主要来源于循环。循环是应用程序中耗时较长的代码,将其展开放在硬件上执行可以增加其并行性,提高性能,但同时循环展开也占用了更多的硬件面积。结合循环展开、循环流水灯面向硬件的并行优化技术,一段应用程序可能会有上百种不同的硬件实现方式[ 6]。
Stitt[ 7]提出了一种BUB启发式算法,同时解决软硬件划分问题及划分中的子问题:硬件多种实现方式选择问题,并将该问题称为PIE(Partitioning w/multi-version implementation exploration)。文献[7]是第一个在求解划分问题的同时确定硬件实现方式的方法,实验结果表明,与FI(选择最快速的硬件实现方式)方法和NE(不考虑多种实现方式,使用最简单的硬件实现方式)方法比较,PIE达到的平均加速比要高于FI和NE。但BUB启发式算法采用了贪婪算法,易陷入局部最优。
遗传算法(Genetic algorithm,GA)是一种模仿生物进化过程的全局优化随机搜索算法,具有简单、通用性高、鲁棒性强等优点,据此本文提出一种改进遗传算法求解PIE问题,算法根据硬件多种实现方式的延时-面积互斥特征,结合Q-学习算法与贪婪规则,改进遗传算法的变异算子,增强遗传算法的局部搜索能力。实验结果表明,本文方法具有良好的效果。
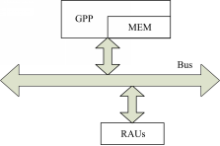
本文采用的目标系统结构是由一个GPP和一个RAU构成的可重构混合架构,如图1所示。GPP和RAU以松耦合的方式实现数据通信,GPP从存储器MEM中读取数据并提供给RAU,RAU独立执行计算,计算完成后再将计算结果写回GPP,GPP和RAU不能并行执行。该结构已被应用在多个领域[ 8, 9]。
循环有多种硬件实现方式,包含循环的函数等粗粒度程序结构自然也有多种硬件实现方式。因此本文的划分粒度可以是循环、函数等。为方便问题描述,本文选取函数为划分粒度,以函数调用图作为输入来描述PIE问题:给定一个调用图的节点集合,及每个节点的硬件实现方式集合,确定哪些节点应该在硬件上实现,以及在硬件上实现时采用哪一种实现方式,目标是在满足给定硬件面积约束 aconstraint的条件下,最小化应用程序总体运行时间 tsys实现性能的最优化。
PIE问题的形式化描述如下:划分算法的输入用三元组< R, aconstraint, ttotal>表示, ttotal是当整个应用程序都在软件上运行时的总运行时间, R是节点集合,可表示为二元组< tSW, I>, tSW是一个节点在软件上的运行时间, I是一个节点的所有硬件实现方式的集合,可用三元组< a, thw, tcomm>表示,其中 a、 thw、 tcomm分别是一种硬件实现方式所需的硬件面积、运行时间及软硬件间通信时间。问题定义为:将 R中的每一个节点选择为0或者1,创建一个解集合 S,使划分目标最小,划分目标如式(1)所示:
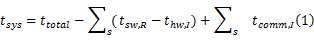
式中: tsw, R是集合 R中一个节点的软件运行时间; thw, I是该节点被选定的硬件实现方式的硬件运行时间; tcomm, I是使用该硬件方式时所需的通信时间。除减少性能外,每一个划分集合 S还必须满足下列约束条件,如式(2)所示:
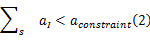
式中: aI是集合 S中实现每一个节点的硬件面积。
遗传算法本身具有较强的全局搜索能力,但局部搜索能力较弱。在选择、交叉、变异算子中,遗传算法的局部搜索能力主要依靠变异算子,该算子的随机变异策略容易对优秀的染色体造成破坏,产生较差的个体。因此本文提出了一种改进的遗传算法,该算法依据硬件实现方式的延时-面积互斥特征,采用基于Q-学习算法的自适应变异算子,增强遗传算法的局部搜索能力。
改进的遗传算法主要包括以下几个步骤:①初始化种群及Q表;②对种群中父代个体进行选择、交叉操作;③根据种群中各个个体的状态,使用Q学习算法,从设定的动作集中自适应选择变异策略,产生子代个体;④使用子代个体代替父代个体;⑤重复②、③、④步骤,直到满足终止准则,选择出最优解。
Q-学习算法[ 10]是强化学习中的重要算法,也是被广泛使用的强化学习算法之一。通过Q-学习算法,智能体(Agent)能够通过学习适应其所在的环境(Environment),根据所处的状态选择合适的动作;同时Q-学习算法由于具有模型无关的特点,在很多领域都能够得到较好的应用。
Q-学习算法的过程如下:首先初始化 Q( s, t)值为任意值,然后在每个离散时间步 t,Agent根据感知到的状态 st以及行为选择策略(采用Softmax策略或者ε-greedy策略)选择动作 at,执行动作后,转移到状态 st+1并得到立即回报 rt,Agent通过该立即回报修正 Q( s, a)的值。其中 Q( s, a)是Q-学习算法的评估函数,表示Agent在状态 s下执行动作 a所获得的回报折扣和,其基本形式如式(3)所示:
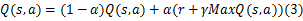
式中: α为学习率; γ为折扣因子; α和 γ为常数。
在基于遗传算法的软硬件划分中,二进制编码是最早,也是最常用的编码方案,将集合 R中的节点映射到位串空间的0和1,然后在位串空间进行遗传操作。在二进制编码中,一般用0表示节点由软件实现,用1表示节点由硬件实现。然而,在PIE问题中,每个划分对象有多种硬件实现方式,简单的0、1编码已无法满足设计需求,因此本文采用浮点数编码方案,记浮点数向量:
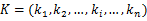
式中: K表示遗传操作的染色体, n是节点个数,个体 ki的取值如式(4)所示:

式中: m是一个节点的硬件实现方式个数; j是区间(0, m]中的正整数。
例如对于一个含有8个节点的应用程序,每个节点都有4种硬件实现方式,如果编码向量为(0.1,0.3,0.1,0.4,0,0.7,0.8),则表示节点1、3、5用软件实现,节点2、4、6、7分别使用各自的第1、2、3、4种硬件实现方式实现。
在遗传算法中,适应度函数是种群中染色体质量的判断标准,有多种设定方法,本文采用惩罚函数法,将目标函数转换成无约束条件的函数寻找最优解。具体方法是在目标函数上增加一个与面积约束有关的惩罚项,对超出硬件面积的部分加以限制。如式(5)所示, f( x)表示整体执行代价, p为体现惩罚力度的常数:
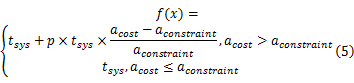
在遗传算法中染色体适应度函数值越高表示个体越优秀,而本文的划分目标是求解目标函数的最小值,因此适应度函数 Fit( f( x))以式(6)方式定义,其中 cmax表示当前种群中最优个体与最差个体的执行代价之和。
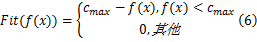
本文算法采用轮盘赌选择策略,每一轮选择产生一个[0,1]区间的随机数,将这个随机数作为选择指针确定被选个体。一轮选择结束后,将被选个体放回,进行下一轮选择。当被选个体数达到种群设定规模时,采用精英保留策略,使用上一代最好的个体将本轮最差的个体替换。
对于交叉操作,算法采用单点交叉策略,从0到染色体长度 n之间随机选择一个整数作为交叉点,然后随机选择2条染色体,以该点为分界交换染色体基因码。本文中交叉率固定为1。
在实际使用过程中,减少硬件面积与提高加速效果在某种程度上是矛盾的,因此需要采用Q-学习算法对不同的划分结果采取不同的策略进行改善。例如算法向加速效果更好的方向进化或者向硬件面积减少的方向进化。
算法的变异算子结合Q-学习算法和贪婪规则,自适应地选择合适的变异方向,产生适应值更高的个体。本文制定变异策略的主要工作包括定义状态集 S、行为集 A、行为选择策略以及奖赏值 r。
(1)定义状态集S
在理论上,遗传算法中的每个不同染色体都可以表示一种状态,但若如此定义,会造成状态空间过大的情况,因此需要对染色体进行分类。本文设计状态集时,从成本和性能两方面考虑,即一方面考虑程序耗用硬件面积,另一方面考虑程序的执行代价 f( x)。将染色体状态用
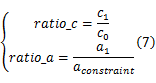
将得到的ratio_ a按范围分别分成[0,-0.8),[0.8,-0.82),[0.82,-0.84),…,[1.18,-1.20),[1.20,-∞)等区间;ratio_c分成[0,-0.02),[0.02,-0.04),[0.04,-0.08)…[1.18,-1.20),[1.20,-∞)等区间,通过不同区间来区分染色体的状态。
(2)定义行为集 A
算法使用贪婪规则定义行为集 A,贪婪规则基于加速效果和减少硬件面积两个因素,两个因素的定义如下:设一个节点的软件运行时间为 t0,占用硬件面积 a0的值为0,有 m种硬件实现方式,硬件运行时间分别为 t1, t2,…, tm;消耗硬件面积分别为 a0, a1,…, am,则加速效果speedup如式(8)所示;而减少面积效果reduce_area如式(9)所示;count表示该节点的执行次数:
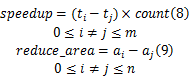
以式(8)(9)两个因素为基础,使用以下4种贪婪规则对行为集进行定义:①全局搜索加速效果最佳的实现方式;②全局搜索减少面积最多的实现方式;③局部搜索加速效果更好的实现方式;④局部搜索减少面积更多的实现方式。其中策略①、②是从全局角度考虑加速效果和硬件面积消耗的影响;而策略③、④是从局部上进行加速或面积的调整。
(3)行为选择策略
本文算法在学习过程中使用Soft max策略选择行为,设染色体在状态 st下,状态 -动作对的 Q值为 Q( st, at),状态 st下动作集为 A,则选择行为概率 p( at)如式(10)所示:
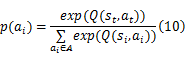
(4)定义奖赏值 r
奖赏值 r的取值范围为{ -1,0,1},将染色体经过动作 a后的适应度与之前的适应度进行比较,如果适应度值更高则将 r设为1;如果适应度值无变化,则将 r设为0;如果适应度降低则将 r设为-1。
本文在算法每次迭代时都保存最佳个体,设定一个自然数 C,认为连续 C代最佳个体相同时算法收敛,并结束运算。
为了验证算法的可行性,本文使用基准测试用例MiBench中tmndec、tmn、djpeg、cjpeg、jm10.2五个应用程序作为输入,以函数为节点,使用GCC的gprof工具[ 11]获得五个应用程序的函数调用图,节点数量分别为27、36、88、101、215,节点和边的运行时间及硬件面积采用伪随机数,且按以下原则生成:①硬件运行时间、通信时间之和比软件运行时间短;②一个节点的硬件实现方式个数取1~8的随机数;③同一个节点的多种硬件实现方式中,占用硬件面积越大的实现方式,其相应的硬件运行时间越短;④为了使不同节点的实验结果具有可比性,硬件面积约束值 aconstraint与节点数相关,计算公式如式(11)所示:
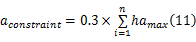
式中: n是指节点个数; hamax为各节点的硬件实现方式所用的最大硬件面积,本文设定总硬件面积约束值为各个节点最大硬件面积和的30%。
算法测试环境为Intel(R) Core(TM)2 2.26 GHz CPU,400 MB内存;操作系统为Fedora 10。本文使用C++编程实现了BUB算法、标准遗传算法及本文算法。表1列出了分别使用三种算法解决PIE问题的实验结果,其中标准遗传算法采用随机变异原则,变异率取0.01,其他参数与本文算法相同。其中 N表示节点数, aS是划分后应用程序所占硬件面积,提高百分比是指标准遗传算法和本文算法相对于BUB算法提高的百分比。从表1数据可以看出,对于所有节点,本文算法划分结果 tsys比BUB算法和标准遗传算法都要小,且本文算法提高的百分比要比标准遗传算法大,可见在满足硬件面积约束的条件下,本文算法生成的解要优于标准遗传算法及BUB算法。
| 表1 BUB算法、标准遗传算法与本文算法的实验结果对比 Table 1 Result comparison of BUB algorithm, standard GA and proposed algorithms |
本文对比了BUB算法、遗传算法和本文算法的收敛性。图2为节点数为215、88的应用程序示范系统运行10次, 划分过程中平均每代最佳有效个体的目标函数曲线。从图2中可看出,经过多次迭代后,与标准遗传算法相比,本文算法收敛速度更快,得到的解更好。本文算法的初期收敛动力来自于变异算子本身,遗传算法本身的大量迭代次数又保证了Q-学习算法的快速收敛,因此本文算法的收敛速度比较快。
作者提出了一种改进的遗传算法,该算法在求解软硬件划分问题的同时解决了硬件多种实现方式的探索。为了验证本文算法的可行性,分别测试了MiBench中五个应用程序,通过与BUB算法、标准遗传算法进行比较,结果表明本文算法的搜索质量和算法执行时间都得到了提升。另外划分过程中生成的目标函数曲线,验证了本文算法具有较好的收敛性。本文针对PIE问题的求解,改进了遗传算法的变异算子,而其他对遗传算法的改进方法(例如改进种群初始化、改进交叉等)也可以与本文算法相结合,这也是下一步的研究工作。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|