引用本文
陈涛, 邓辉舫, 刘靖. 基于密度聚类和多示例学习的图像分类方法. 2014, 44(4): 1126-1134
[CHEN Tao, DENG Hui-fang, LIU Jing. Image categorization method using density clustering on region features and multi-instance learning. Journal of Jilin University Engineering and Technology Edition, 2014, 44(4): 1126-1134]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于密度聚类和多示例学习的图像分类方法
陈涛, 邓辉舫, 刘靖
华南理工大学 计算机科学与工程学院,广州 510006

作者简介：陈涛（1979-）,男,博士研究生.研究方向:机器学习,图像分类.E-mail:c.tao01@mail.scut.edu.cn

基金:国家自然科学基金项目（61003174）;
摘要

针对图像的低级特征表示与高级概念之间的语义鸿沟,本文利用密度聚类获得的簇分布信息和多示例学习框架在区分歧义性对象上的特点,提出了一个基于区域特征密度聚类和多示例学习的图像分类方法(DCRF-MIL)。该方法首先将每个图像分割为多个区域,将所有区域组成一个集合,在这个区域集合上,使用密度聚类算法学习到区域特征的簇分布信息;然后,将图像看作包,区域看作包中的示例,基于区域特征的簇分布信息,将包映射为簇分布空间上的一个向量作为包的特征,使得包特征带有图像区域的语义信息;最后,使用支持向量机算法,在带有包特征的训练集上训练分类器,对测试图像进行分类。在Corel图像集和MUSK分子活性预测数据集上的实验表明,DCRF-MIL算法具有分类精度高和参数易于选择等特点。

关键词: 人工智能; 图像分类; 多示例学习; 密度聚类; 支持向量机
中图分类号:TP391.4 文献标志码:A 文章编号:1671-5497(2014)04-1126-09
Image categorization method using density clustering on region features and multi-instance learning
CHEN Tao, DENG Hui-fang, LIU Jing
School of Computer Science and Engineering, South China University of Technology, Guangzhou 510006, China
Abstract

In order to narrow the semantic gap between low-level visual features and high-level semantic concepts in image categorization, the clustering information from a density clustering algorithm and the characteristics of multi-instance learning framework in distinguishing ambiguous object are exploited. An image categorization method is proposed using Density Clustering on Region Features and Multi-Instance Learning (DCRF-MIL). First, the DCRF-MIL divides each image into number of regions and relines up all regions into a collection; then it uses a density clustering algorithm to learn the potential distribution information of the region features in the collection. Second, it treats an image as a bag and the regions as instances in the bag. Based on the cluster distribution information of region features, the bag is mapped into a vector in the cluster distribution space. Finally, a support vector machine classifier is constructed to predict the class label of the unlabeled image. The experiments on the Corel image data set and MUSK molecular activity prediction data set show that the DCRF-MIL method has high classification accuracy and it is easy to select its parameters.

Keyword: artificial intelligence; image categorization; multi-instance learning; density clustering; support vector machine
0 引 言

当图像数量较少时,人们根据先验知识,人工分类图像准确可行。但随着数字图像数量的增长,仅依靠人工对图像进行分类则成为了一件不现实的任务。此外,由于图像存在多样性和歧义性,图像的低级特征表示与高级语义概念之间的鸿沟,使得自动分类图像是一项困难的工作[ 1]。近二十年来,相关研究人员提出了许多图像自动分类方法,可以简略地分为基于图像全局特征的方法和基于区域特征的方法。由于一幅图像由多个区域组成,各个区域具有不同的语义内容,基于区域特征的图像分类方法更符合图像的语义表示。因而,受到许多学者的关注[ 2, 3]。

1997年,Dietterich等人在药物活性分子预测研究中,提出多示例学习的概念[ 4]。在多示例学习框架中,训练集由若干个具有标签的包组成,每个包含有若干个没有标签的示例。若一个包中至少有一个示例为正类,则该包被标记为正包;若一个包中所有示例都为负类,则该包被标记为负包。希望学习系统通过对训练包的学习,能够正确预测出新包的标签[ 5]。由于图像分类与多示例学习问题的假设十分相似,近年来,有学者提出结合多示例学习框架来分类图像。将图像看作多示例学习中的包,图像分割后的多个区域看作包中的示例,这样,就将图像分类转化为多示例学习问题来对待[ 6, 7, 8]。Maron等人提出了DD算法[ 9],是在高维空间中寻找一个取得多样性密度函数最大值的点示例,与这个示例的距离是否大于一个阈值来判定为正类或者负类;Zhang等人结合多样性密度函数和期望最大值算法,提出EM-DD算法[ 10];李展等提出了一个基于谱聚类和多示例学习的图像检索方法[ 11],是通过谱聚类找到一个包含点数最多的聚类中心,选择正包中一个与该聚类中心距离最近的示例作为包中正示例的代表;Andrews等人提出的MI-SVM算法[ 12],是选择一个最大可能示例的特征代表包特征来最大化SVM分类间隔;Yang等人提出ASVM-MIL算法[ 13],针对正、负包中示例数不对称的情形,分别定义不同的正、负包误差损失函数来优化SVM算法的分类决策超平面;路晶等提出使用多示例学习的启发式SVM算法来处理图像自动标注[ 14],是通过迭代改变一个示例的类别,以最大化SVM的分类间隔;Chen等提出了DD-SVM[ 15]和MILES[ 16]两个算法,都是通过构造投影空间,将包在投影空间上非线性投影为一个向量,使用支持向量机求解MIL问题,但构造投影空间的方法不同。上述算法存在捕获的单一示例特征代表包特征,难以精确反映图像的语义信息、没有事先学习区域特征的潜在分布信息、示例原型没有明确的语义、没有利用未标签数据参与训练阶段的学习等局限。本文将区域特征密度聚类与多示例学习框架相结合,提出了一个新的多示例学习分类图像算法(Density clustering on region features and multi-instance learning,DCRF-MIL)。

1 DCRF-MIL算法

假定一组有 l个已标签的训练图像集 L={ <I1, y1 >, <I2, y2 >,…, l, yl>}, u个未标签的测试图像集 U={ Il+1,…, Il+u}, Ii={ ri1, ri2,…, }, rij∈ Rd, i=1,…, n; j=1,…, ni, ni为图像 Ii的区域数, d为区域特征的维数, yk∈{1,…, c}; k=1,…, l; c为类别数, l+u=n。图像 Ii由多个区域 rij组成,只有区域具有特征,图像没有特征,图像 Ii的多个区域 rij共享图像 Ii的标签。我们的目标是在 L集上学习一个分类函数 f( x),使得 f( x)能正确预测未标签图像 U的分类, x是一个由多个区域组成的图像。

在多示例学习框架下,一幅图像 Ii被看作多示例学习中的一个包 Bi,它的区域 rij被看作为包中的一个示例 Bij。这样,包有标签没有特征,标签为图像的标签;示例有特征没有标签,特征为区域特征,包中的多个示例共享一个包的标签。如果将包的标签直接作为包中示例的标签,由于正包中存在不定的负示例(背景区域的存在),这样则会产生较大的标签噪声,影响分类器的性能[ 17]。一个可行的方法是为每个包构造一个包特征,这样就能使用有监督学习算法来分类。在包特征的构造中,我们通过将包向所有区域特征聚类形成的分布空间上投影来生成。

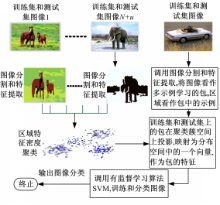
本文提出的DCRF-MIL算法流程图如图1所示。

图1 DCRF-MIL算法的流程图Fig.1 The flowchart of the DCRF-MIL algorithm

首先,将训练集和测试集的图像分割成多个区域,所有区域特征组成一个集合,使用密度聚类算法学习到区域特征的簇分布信息;其次,将图像看作包,区域看作包中的示例,将包在簇分布空间上投影,构造出一个包特征。最后,在带有包特征的训练集上训练SVM分类器,用这个分类器对测试集图像进行分类。本文的包特征生成方法不同于其他多示例学习算法,一是考虑了测试图像集(未标签图像)的信息,测试集数据被加入到DCRF-MIL的训练阶段;二是包特征来源于全体区域特征的簇分布信息,不依赖单个和少数示例。

1.1 图像分割和特征提取

图像分割成多个区域是DCRF-MIL算法的预处理工作,本文参考文献[16]的图像分割方法,另附加一维特征。首先,将图像分片成4*4像素的不重叠小块,提取小块的3维LUV平均颜色特征。为了提取出图像的纹理特征,对小块4*4像素进行一级Daubechies-4小波变换,分解成LL、LH、HL、HH等4个子带,每个子带含有一个2*2系数。LH、HL、HH3个子带系数分别反映小块在垂直、水平、对角方向上的变化信息,分别提取它们系数的均方根值作为一维特征,共3维。其次,使用修改的 k-means算法聚类小块,多个具有相似颜色和纹理特征的小块聚类成为一个区域,区域特征为多个小块特征的平均值。 k-means算法的 k值不需指定,从 k值设为2开始,不断增加,直到满足一个停止条件,来确定 k值[ 18]。第三,由于形心极惯性矩不随图形轮廓的平移、旋转发生变化,提取一、二、三阶归一化极惯性矩3维特征附加到区域特征上,作为区域的形状特征。此外,为了处理密度聚类形成的超球面形状簇的区分,我们附加一维特征,初值置0。这样,一个区域由10维特征表示。

1.2 区域特征密度聚类

经过图像分割后,一幅图像 Ii由多个区域{ ri1, ri2,…, 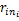}组成。把所有图像区域特征重新排列,形成一个集合 collection={ xp|xp∈ rij}, p=1,…, n; i=1,…, N; j=1,…, ni。在这个集合上使用聚类算法去学习区域特征潜在的分布信息。由于密度聚类方法能够聚类任意形状的簇[ 19],故本文采用它。

定义1 x的 ε邻域: ε( x) ={ xi|xi∈ Rd,‖ x, xi‖≤ ε},其中 ε≥0,‖ x, xi‖为点 x, xi之间的欧氏距离。

定义2 x的点密度: density( x) = 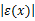,表示 x的 ε邻域的点个数。如果 density( x)≥ θ, θ为最小点数,则称 x点为核心点。

定义3 直接密度可达:如果点 y∈ ε( x), and density( x)≥ θ,则称点 y是从点 x出发直接密度可达到的。

定义4 密度可达:如果存在顺序点 x1, x2,…, xp∈ X, xi与 xi+1是直接密度可达,则称点 x1与点 xp密度可达。

基于以上定义,区域特征密度聚类算法描述如下.

输入:区域特征的集合 collection={ x1, x2,…, xn}, n为所有图像区域的总数, xi为一个10维区域特征向量

输出:聚类簇空间 W1, W2,…, Wk和簇中心点 C1, C2,…, Ck, k为聚类簇数

Step1 初始化, S1 =collection, k=0

Step2 While ( S1不为空集)

从 S1中任选取一个点 x

if( density( x) <θ) then S1 =S1 -{ x};将 x标为噪声点}

else { k=k+1;

找出 collection中所有与 x密度可达的点,生成点集合 T; //T中可以含有原来被标为噪声的点

x∪ T→ Wk; S1 =S1 -Wk

endif

end //{while}

Step3 去除噪声点后,形成聚类簇空间 W1, W2,…, Wk,计算出 k个簇中心点 Ci= 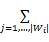{ xj∈ Wi} /|Wi|, i=1,…, k。

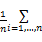
邻域半径 ε的选取极大地影响着聚类的性能。为了选取合适的 ε,我们将之转为对点 x的 K近邻 K值选取, K较 ε易于选取。具体为:设 xi的 K近邻距离 K_dist( xi) = ‖( xi, pj)‖,其中 pj为 xi的 K个最近邻点。这样, ε是所有点 x的平均 K近邻距离: ε= K_dist( xi)。

之前1.1中定义了一个附加特征,即区域的第10维特征,并置为0。因而,簇中心点 Ck的第10维特征也为0。由于两个具有同心圆的超球面形状簇的中心点特征是相同的,为了区分两者的不同,我们对簇中心点 Ck的第10维特征计算为: 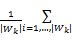‖ xi, Ck‖, xi∈ Wk。

1.3 构造包的特征

聚类后,形成 k个簇空间和 k个簇中心点。每个簇空间由一组语义信息相关的区域特征组成,我们可以将它称为一个“视觉语义”概念。每个簇中心点是“视觉语义”的特征表示,为一个簇空间中所有区域特征的平均值。如果我们直接将 k个簇空间作为图像的分类结果,则有两个原因阻碍分类精度的提高:一是图像的歧义性,即一幅图像由多个区域组成,每个区域有不同的语义信息。这样,一幅图像可能有多个类别标签;二是密度聚类算法没有利用有标签图像的标签信息。但聚类后形成的 k个簇空间反映了所有区域特征的分布信息,这有助我们基于这个分布信息构造出一个包的特征。

将一个包与一个簇中心点的距离看作包与这个簇所代表的“视觉语义”概念两者间的相似概率,如果距离愈近邻,两者愈相似,相似概率愈大。基于区域特征的簇分布信息,将每个包 Bi向 k个簇空间上投影映射,得到一个包特征:

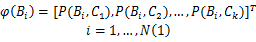
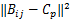
在公式(1)中的 P( Bi, Cp)计算中,由于一个包有多个示例,我们选取与簇中心点 Cp最近邻的一个示例的距离作为包与簇中心点 Cp之间的相似概率: P( Bi, Cp) = exp( - ),1≤ p≤ k;1≤ j≤ ni。 Bij是包 Bi的一个示例, Cp是一个簇中心点, ni是包中的示例个数。

通过向 k个簇空间的投影映射,包中的多个示例特征融合为一个新的包特征,包特征带有图像区域的语义信息,为一个 k维向量,每一维代表包与一个“视觉语义”概念之间的相似概率。

1.4 SVM分类器

得到训练集和测试集上的包特征后,训练集上包的标签是已知的,为训练图像的标签,就能利用有监督学习方法SVM分类器来分类图像。

引入松弛变量的SVM目标优化函数:

式中: yi为训练图像的标签, Xi为训练图像的包特征; C>0是惩罚因子,用于控制目标函数对错分样本惩罚的权重,是一个常量; ξi是松弛项,是需要优化的变量; b是待求变量, W和 ξ是待求向量。引入拉格朗日乘子,将式(2)带不等式约束的目标函数化为:

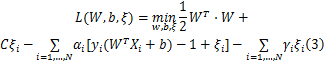
式中: αi和 γi是拉格朗日乘子。式(3)是一个二次凸规划问题,可以转化为其对偶函数来求解。通过对变量 W、 b和 ξi求偏导数,并代入式(3),得其对偶函数为:

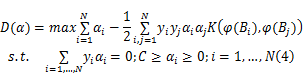
式中: K( )为核函数。由于式(3)是一个凸函数,存在唯一的全局最优解,且满足Karush-Kuhn-Tucker条件,因而,公式(3)与其对偶函数公式(4)等价[ 20]。通过求解公式(4),可以解出 α*,由 α*解出 W*和 b*。

预测图像的标签:

1.5 DCRF-MIL算法描述

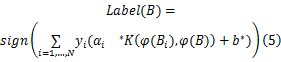
输入:已标签图像集 L={ <I1, y1 >, <I2, y2 >,…, <Il, yl>}

输出: u个未标签的测试图像集 U={ IN+1,…, IN+u}测试图像的标签

(1)置 D为空集。

(2)将 L+U中的每个图像 Ii分割成多个区域 ri1, ri2,…, ,提取出10维区域特征。

(3)将所有区域排列在一起形成区域集合 collection,对 collection进行区域特征密度聚类,生成投影空间簇 W1, W2,…, Wk和簇中心点 C1, C2,…, Ck, k为簇数。

(4)将图像看作多示例学习中的包,图像中的区域看作包中的示例( Ii对应 Bi, Rij对应 Bij)。对 L+U中的每个包,根据公式(1),得出包的特征 φ( Bi)。对 L集, yi=li; D=D∪ <φ( Bi), yi>; i=1,…, N。

(5)在 D上训练SVM分类器,解出 α*, W*和 b*。

(6)根据式(5),输出测试集 U中图像的标签。

2 实验结果

本文进行了3组实验,采用分类精度来评价算法的性能。分类精度是预测出来的图像标签与图像实际标签比较,得出的正确分类的百分比。第1组为DCRF-MIL算法在Corel图像库上进行图像分类,并与其他4个MIL算法、1个视觉词袋算法进行比较;第2组为附加的第10维特征、密度聚类参数邻域半径、训练图像数对DCRF-MIL算法的分类精度影响;第3组为在MUSK数据集上,DCRF-MIL算法与其他MIL算法的分类精度比较。

2.1 DCRF-MIL算法在Corel图像库上的分类精度

Corel图像库有Corel 1000和Corel 2000两个图像集[ 16],来自http://www.cs.olemiss.edu/~ychen/ddsvm.html。Corel 1000中有10类图像,每类有100幅图像,共1000幅图像,存储格式为JPEG文件。Corel 2000则有20类,共2000幅图像。实验采用2折交叉验证方法,随机划分数据集,一半作为训练集,余下的作为测试集。10次随机划分,取平均分类精度。

SVM算法代码来自LibSVM软件包(http://www.csie.ntu.edu.tw/~cjlin/libsvm/),采用“一对余下”的方法区分多类问题,共训练 c个(类别数)SVM分类器,选取输出值最大的SVM分类器作为被预测图像的标签。SVM的核函数采用径向基函数 K( x, z) =exp( -γ‖ x-z‖2)。参数 γ和式(2)的代价参数 C(在训练误差和泛化能力上折衷取值)的选取,在各自设定区间上均匀分成10个子区间,共100种组合,选择得出分类精度最优的一组数值作为参数值,选取 C=700, γ=0 .1。

实验1 在Corel图像库上的分类精度比较

本文将DCRF-MIL与其他4个MIL算法和1个视觉词袋算法:DD[ 9]、MI-SVM[ 12]、DD-SVM[ 15]、MILES[ 16]、Bag-of-Visual-Words(BoVW)进行比较。与其他4个MIL算法比较,它们之间的不同主要是采取了不同的包特征构造方法。DD算法依赖于由多样性密度函数确定的最大值点示例。MI-SVM算法是选择包中最有可能示例的特征作为包特征。DD和MI-SVM这两个算法依赖于单个示例特征,而复杂图像难以由单个示例捕获。DD-SVM算法是通过对包向析取出来的示例原型进行映射获得包特征,其示例原型没有明确的语义信息。MILES算法的包特征是通过向所有示例投影获得,并利用SVM分类器进行特征选择,其包特征没有事先学习区域特征的分布信息,且存在高维表示和维数冗余问题。另外,以上这4个算法,都没有利用测试集数据参加训练阶段的学习。而DCRF-MIL算法的包特征是基于密度聚类获得的簇分布信息,通过包中示例在簇分布空间上投影映射获得,它取决于所有区域特征形成的簇分布信息,不依赖于单个或少数示例。此外,测试集数据被加入到密度聚类算法中,未标签图像信息被利用,使得簇分布信息更为准确。

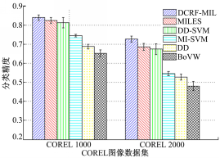
视觉词袋算法[ 21](BoVW)是先从所有图像中提取出每幅图像的特征点,或者是将每幅图像分割成小块,通过聚类,将每个类簇作为一个视觉字,集合它们组成视觉词袋。再对图像向视觉词袋进行映射得出图像的特征,使用有监督学习分类器分类。DCRF-MIL算法与BoVW算法的不同在于:①DCRF-MIL是先在每幅图像上聚类小块,分割成区域;再密度聚类所有图像的区域。通过两次聚类,使得聚类相对较易,且形成的类簇数较少。而BoVW是在特征点或者是小块上进行一次聚类,使得视觉字的个数非常大。②在构造图像的特征时,DCRF-MIL是通过包与 k个簇中心点的相似概率来获得 k维特征,而BoVW是通过一个词频直方图来获得,特征维数为视觉词袋的尺寸,它远远大于DCRF-MIL的 k维特征。为了与DCRF-MIL的实验比较,BoVW算法选择划分4*4小块的方法,小块特征为共6维的颜色和纹理特征,视觉词袋的大小取5000,没有使用去停止词、视觉字的特征选择等技术,实验结果见图2。

DCRF-MIL等6个算法在Corel图像库上的分类精度比较结果见图2。

图2 Corel图像库上的分类精度Fig.2 Accuracy on Corel dataset

从图2可以看出,DCRF-MIL算法在Corel1000和Corel 2000上的分类预测精度,均是6个算法中最好的,分别为84.1%、72.8%,比MILES算法分别高出1.5%、4.1%,比DD-SVM分别高出2.6%、5.3%,比MI-SVM分别高出9.4%、18.2%,比DD分别高出15.2%、20%,比BoVW算法分别高出18.8%、24.7%。

实验2 DCRF-MIL算法分类精度的混淆矩阵

为了详细分析算法性能,给出了DCRF-MIL算法在Corel 1000图像库上的分类精度混淆矩阵,见表1。

表1所示是DCRF-MIL算法的分类混淆矩阵,对角线上的数字(加粗体)表示算法在每类上的分类精度,非对角线上的数据表示相应的错误率。DCRF-MIL算法在10个类别上的分类精度都较高,但在Cat 0(African people villages类)、Cat 1(Beach类)、Cat 2(Historical building类)和Cat 8(Mountains and glaciers类)的错分率较大,这可能是因为这些类图像含有较多的与其他类图像共有的视觉特征相似、语义相关的图像区域,DCRF-MIL算法较难区分它们之间的差异。从表1的Table(1,8)和Table(8,1)项可以看出,Cat 1和Cat 8之间的相互错分率很大,分成Beach类的错误率10.9%来自于Mountains类,分成Mountains类的错误率11.8%来自于Beach类,可能是因为这两类图像大量含有天空、河流、湖水和海洋等图像区域。

表1 DCRF-MIL在Corel 1000的分类精度混淆矩阵(%) Table 1 Accuracy confusion matrix of DCRF-MIL
2.2 第10维特征、密度聚类参数邻域半径、训练图像数对DCRF-MIL算法分类精度的影响

实验1 附加的第10维特征对分类精度的影响

在Corel 1000集上观察附加的第10维特征(1.1和1.2节所述)对算法的影响,分类精度见表2。

从表2看出,DCRF-MIL算法在10维区域特征表示下的分类精度比采用文献[16]的9维区域特征表示高出1.4%。这可能是因为:第10维特征能度量出类簇的紧凑程度,它有助于向类簇中心点映射生成的包特征更能反映出区域特征簇的分布信息。此外,在“恐龙”类和“大象”类图像的分类精度,10维特征表示比9维特征分别高出3.9%、3.5%。这是因为,在聚类“恐龙”和“大象”类图像时,碰到了一些类簇呈同圆心的超球面形状,9维特征表示会出现不相同类簇,但类簇中心点的位置相接近的情况,这对包特征的映射生成产生影响,降低分类性能。而10维特征表示能使不相同类簇的中心点位置也不相同。

实验2 密度聚类参数邻域半径 ε对分类精度的影响

表2 DCRF-MIL在不同区域特征表示下的分类精度 Table 2 Accuracy of DCRF-MIL on different representation for region feature %

根据1.2节所述,我们将邻域半径 ε转为对区域 K近邻的 K值选取。在Corel 1000集上, K取3至15,取500幅图像为训练集,余下500幅为测试集,密度聚类算法中的点 x是核心点的最小点数 θ,设定为7,DCRF-MIL算法的分类精度如图3所示。

图3 在Corel 1000上DCR-MIL算法不同 K值的分类精度Fig.3 Accuracy of DCRF-MIL when different K values

从图3可以看出,算法的性能受 K值的影响较大。 K值从3变化到15,精度在区间[0.763,0.841]波动。在 K=11时达到最大值0.841;当 K大于11时,分类精度出现下降。这可能是因为 K值影响聚类产生的簇数。 K值愈小,由其决定的密度算法的领域半径就愈小,使得聚类形成的簇数过多,向簇空间上映射得到的包特征存在维数冗余等问题。 K值过大时,则会产生较相邻的、但不相似的两个簇合并的情况,这影响了包特征表示图像语义信息的准确比率。

实验3 训练图像数不同对分类精度的影响

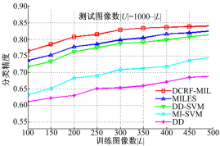
在Corel 1000图像集中,我们把训练图像数从100增长到500(每类随机选取10个图像增长到50个图像),测试图像数(未标签图像数)为Corel 1000集图像总数减去训练图像数,5个算法取得的分类精度如图4所示。

图4 在COREL 1000上,训练图像数不同时的分类精度Fig.4 Accuracy when the number of training set is varied

从图4看出,随着训练图像数的增加,5个算法的分类精度均有提高。还可以看出,DCRF-MIL算法在较小的训练图像数时,就能取得较好的分类精度,在训练图像数为300幅时接近它的精度峰值,而其他4个MIL算法的分类精度受训练图像数的影响较大。这可能是因为,DCRF-MIL算法的包特征生成是基于所有图像(训练集和测试集)区域特征的簇分布信息,测试集图像参与了聚类计算。不管训练图像数多少,其包特征都是相同的,训练图像数只影响它的SVM分类器性能。而其他4个MIL算法,测试集图像不参与它们的训练阶段的学习,故而训练集图像数能很大程度地影响它们的分类精度。

2.3 DCRF-MIL算法在MUSK数据集上的分类精度

MUSK数据集是多示例学习算法的基准测试集[ 9],在研究药物活性分子预测时产生的数据,有两个子集:MUSK1和MUSK2。它们是麝香分子的样本,一个包表示一个分子,包中的示例对应分子的一个低能形态。每个形态用一个166维向量表示。MUSK1包含47个正包和45个负包,包中示例数从2~40不等,平均为5.17个。MUSK2包含39个正包和63个负包,包中示例数从1~1044不等,平均为64.49个。DCRF-MIL算法将训练集和测试集的包中的所有示例组成一个集合,在这个集合上使用密度聚类算法得出示例特征的簇分布信息,去生成包的特征,再进行分类。实验采用10折交叉验证方法,数据集被随机分成10等份,9份用于训练,1份用于测试。取10次的平均分类精度。实验参数的取值采用与2.1节和2.2节相同的方法得出,SVM参数取值 C=600、 r=0 .0001,密度聚类的 K近邻参数取值 K=7时获得了实验的最好性能。

选择DCRF-MIL与其他8个MIL算法:APR[ 4]、mi-SVM[ 12]、MI-SVM[ 12]、MILES[ 16]、ASVM-MIL[ 13]、DD-SVM[ 15]、DD[ 9]、EM-DD[ 10]进行比较。DCRF-MIL等9个算法的实验结果如图5所示。

图5 MUSK数据集上的分类精度比较Fig.5 Accuracy on MUSK dataset

从图5可见,在MUSK1数据集上,DCRF-MIL算法获得了仅次于APR算法的分类精度,而APR算法是专门针对MUSK数据集特征的算法,DCRF-MIL算法不针对特定数据集,没有对MUSK数据集特征进行特定处理,但也获得了较好的分类效果。在MUSK2数据集上,DCRF-MIL算法获得了最好性能。与APR算法相比,提高精度约2.3%,与DD算法比较,提高精度约9%。这可能是因为,大的数据集使得各个类簇中心更能反映出示例特征的分布信息,向各个类簇中心投影生成的包特征带有更多的分子类别信息。

3 结束语

本文将密度聚类算法与多示例学习框架相结合,提出了一种新的多示例学习分类图像方法。该方法先利用密度聚类算法获取区域特征的簇分布信息,在多示例学习的框架下,将包在簇空间上投影构造出一个包特征,使得包特征取决于总体的区域特征分布,不依赖单个和少数示例。在聚类时,考虑了未标签图像参与学习,使得它在较小的训练图像数时就能取得较好的分类精度。将密度聚类参数邻域半径 ε转为对区域 K近邻的 K值选取,这易于选取。在Corel图像集和MUSK数据集上的实验表明,DCRF-MIL算法获得了较好的分类精度,是有效的。

The authors have declared that no competing interests exist.

参考文献
[1] Binder A, Mueller K R, Kawanabe M. On taxonomies for multi-class image categorization[J]. International Journal of Computer Vision, 2012, 99(3): 281-301. [本文引用:1] [JCR: 3.623]
[2] Hu Xiao-hong, Xu Qian, Ma Xin-ming, et al. A novel region-based image annotation using multi-instance learning[C]∥Proceedings of the Second International Workshop on Knowledge Discovery and Data Mining, 2009: 602-605. [本文引用:1]
[3] Song Xiang-fa, Jiao L C, Yang Shu-yuan. Sparse coding and classifier ensemble based multi-instance learning for image categorization[J]. Signal Processing, 2013, 93(1): 1-11. [本文引用:1] [JCR: 1.851]
[4] Dietterich T G, Lathrop R H, Lozano-Pérez T. Solving the multiple-instance problem with axis-parallel rectangles[J]. Artificial Intelligence, 1997, 89(1/2): 31-71. [本文引用:2] [JCR: 2.194]
[5] Foulds James, Frank Eibe. A review of multi-instance learning assumptions[J]. Knowledge Engineering Review, 2010, 25(1): 1-25. [本文引用:1] [JCR: 0.59]
[6] Fu Zhou-yu, Robles-Kelly A, Zhou Jun. Multiple instance learning with instance selection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(5): 958-977. [本文引用:1] [JCR: 4.795]
[7] Babenko B, Verma N, Dollár P, et al. Multiple instance learning with manifold bags[C]∥Proceedings of the 28th International Conference on Machine Learning, ICML2011: 81-88. [本文引用:1]
[8] 陈绵书, 杨树媛, 赵志杰, 等. 多点多样性密度算法及其在图像检索中的应用[J]. 吉林大学学报: 工学版, 2011, 41(5): 1456-1460.
Chen Mian-shu, Yang Shu-yuan, Zhao Zhi-jie, et al. Multi-points diverse density learning algorithm and its application in image retrieval[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(5): 1456-1460. [本文引用:1] [CJCR: 0.701]
[9] Maron O, Lozano-Pérez T. A framework for multiple-instance learning[J]. Advances in Neural Information Processing Systems , Cambridge, MA: MIT Press, 1998: 570-576. [本文引用:4]
[10] Zhang Q, Goldman S A. EM-DD: an improved multiple-instance learning technique[J]. Advances in Neural Information Processing Systems, Cambridge, CA: MIT Press, 2002: 1073-1080. [本文引用:2]
[11] 李展, 彭进业, 温超. 基于谱聚类和多示例学习的图像检索方法[J]. 华南理工大学学报: 自然科学版, 2011, 39(7): 156-162.
Li Zhan, Peng Jin-ye, Wen Chao. Image retrieval based on spectral clustering and multiple instance learning[J]. Journal of South China University of Technology (Natural Science Edition), 2011, 39(7): 156-162. [本文引用:1]
[12] Andrews S, Tsochantaridis I, Hofmann T. Support vector machines for multiple instance learning[C]∥Advances in Neural Information Processing Systems, Cambridge, MA: MIT Press, 2003: 561-568. [本文引用:4]
[13] Yang Chang-bo, Dong Ming, Hua Jing. Region-based image annotation using asymmetrical support vector machine-based multiple-Instance learning[C]∥Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2006, 2: 2057-2063. [本文引用:2]
[14] 路晶, 马少平. 使用多例学习的启发式SVM算法的图像自动标注[J]. 计算机研究与发展, 2009, 46(5): 864-871.
Lu Jing, Ma Shao-ping. Region-based image annotation using heuristic support vector machine in multiple-instance learning[J]. Journal of Computer Research and Development, 2009, 46(5): 864-871. [本文引用:1]
[15] Chen Y X, Wang J Z. Image categorization by learning and reasoning with regions[J]. Journal of Machine Learning Research, 2004, 5: 913-939. [本文引用:3] [JCR: 3.42]
[16] Chen Y X, Bi J, Wang J Z. MILES: Multiple-instance learning via embedded instance selection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(12): 1931-1947. [本文引用:4] [JCR: 4.795]
[17] Zhou Zhi-Hua. Multi-instance learning from supervised view[J]. Journal of Computer Science and Technology, 2006, 6(5): 800-809. [本文引用:1] [CJCR: 0.4]
[18] Wang J Z, Li J, Wiederhold G. SIMPLIcity: Semantics-sensitive integrated matching for picture libraries[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(9): 947-963. [本文引用:1] [JCR: 4.795]
[19] Yang Christopher C, Ng Tobun Dorbin. Analyzing and visualizing web opinion development and social interactions with density-based clustering[J]. IEEE Transactions on Systems, Man, and Cybernetics Part A: Systems and Humans, 2011, 41(6): 1144-1155. [本文引用:1] [JCR: 2.183]
[20] Kundakcioglu O E, Seref O, Pardalos P M. Multiple instance learning via margin maximization[J]. Applied Numerical Mathematics, 2010, 60(4): 14-23. [本文引用:1] [JCR: 1.152]
[21] Yang Jun, Jiang Yu-gang, Hauptmann Alexand er G, et al. Evaluating bag-of-visual-words representations in scene classification[C]∥Proceedings of the 9th ACM SIG Multimedia International Workshop on Multimedia Information Retrieval, 2007: 197-206. [本文引用:1]