定义1 数据点 p的 E_ps邻域:是以数据集合 D中的点 p为圆心,以 E_ps为半径的圆区域。区域中包含的点集合记作 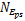( p) ={ q∈ D|dist( p, q)≤ E_ps}。

定义2 数据点 p的密度:是数据集合 D中数据点 p的 E_ps邻域中数据点的个数。

定义3 核心点:如果数据点 p的密度大于或等于Min Pts则称其为核心点,其中Min Pts是由用户指定的一个阈值。

定义4 边界点:是指数据点 q本身不是核心点,但它包含在另外一个核心点 p的 E_ps邻域内,则称 q为边界点。

定义5 噪声点:数据集合中既不是核心点也不是边界点的其他点称为噪声点。

定义6 直接密度可达:设数据点 q是核心点,只要满足数据点 p属于数据点 q的 E_ps邻域,则说数据点 p从数据点 q直接密度可达,记作:

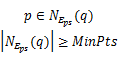
定义7 密度可达:如果存在数据点链 p₁, p₂,…, p_n,其中 p₁ =p, p_n=q, p_i∈ D,1≤ i≤ n,而且有 p_i从 p_i+1直接密度可达,则称数据点 p从数据点 q密度可达。

定义8 密度相连:数据集合 D中,对于给定的 E_ps和Min Pts,如果存在点 o,使得数据点 p和数据点 q都从数据点 o密度可达,则称数据点 p和数据点 q关于 E_ps和Min Pts密度相连。

在DBSCAN算法发现聚类的过程中,先从数据集合 D中找到任一数据点 p,考察点 p,如果 p是核心点,即 p的邻域中点的数目大于等于 MinPts,那么 p的 E_ps邻域中的数据点在接下来的过程中作为种子点,进行进一步考察。具体就是:不断对种子点进行区域查询,如果当前种子点也是核心点,则将它的 E_ps邻域中的点也加入种子集合中。通过这种方式,不断扩展当前数据点所在的类(簇),直到找到一个完整的类(簇)为止,这样就确定了一个关于 E_ps和 MinPts的聚类。如果 p是一个边界点,即 p的邻域中点的数目小于 MinPts,则DBSCAN算法选取数据集 D中的下一个点进行处理。而数据集合中最终剩下的没有被划分到任意类(簇)中的数据点就被标记为噪声点。

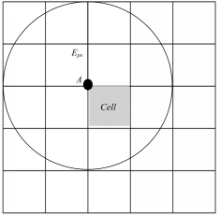
点 p邻域中数据点的数目是通过不断执行区域查询和判断来获取的^{[ 9]},以二维数据为例,网格上的区域查询如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 网格单元上的区域查询Fig.1 Region query on grid cell

每次查询判断返回区域中的所有对象,DBSCAN算法的时间复杂度为 O( n²),可见算法的时间开销很大。另外,算法运行时,所有数据都应该存放在内存中,当数据量增大时,要求较大的内存支持,I/O消耗也很大^{[ 10]}。针对以上两点,本文提出一种网格单元划分方法,优化区域查询操作以减少时间开销。

定义9 网格单元:用户设定一个划分参数 ε,根据这个参数可以将数据空间在每一维上划分为 π个相同长度(即 ε)的区间,每个维度上做相同的划分,从而将整个数据空间划分成边长为 ε的网格。记作网格单元 Cell={ c₁, c₂,…, c_n}, c_i={[ l_ij, h_ij)},1≤ i≤ n,其中 h_ij— l_ij=ε, i表示维度, j表示空间序数,这是一个左闭右开区间。在网格单元划分的过程中,最后一个网格单元的边长可能不足 ε,可以将该边长看作 ε,这样既不会影响计算的准确性,又可保证计算的一致性。

定义10 k-邻接网格集合:网格单元 Cell的 k-邻接网格集合定义为沿网格 Cell的上下左右4个方向各延伸 k个网格边长(即 k×ε的距离)后所构成的矩形区域所包含的网格集合,记作 N_cell。

定义11 E_ps矩形域:以二维网格 Cell的4个顶点为圆心,画4个半径为 E_ps的圆。网格单元 Cell的 E_ps矩形域定义为能够覆盖这4个圆区域的 k-邻接网格集合所构成的区域。

为了便于计算网格单元 Cell的 E_ps矩形域,取网格单元的边长 L_pg=E_ps/γ。显然,当 γ≥1时,网格单元 Cell的 E_ps矩形域为 Cell的 γ-邻接网格集合所构成的区域,边长为(2 γ+1) ×L_pg;当 γ<1时, Cell的 E_ps矩形域为 Cell的1-邻接网格集合所构成的区域,边长为3× L_pg。

图2所示为当 γ=2时,网格单元 Cell的 E_ps矩形域。由图2可以看出,当网格单元 Cell的 E_ps矩形域内的点的数目不足 MinPts时, Cell内任意一点都不可能是核心点,而当网格单元 Cell的 E_ps矩形域内的点的数目大于等于Min Pts时,种子点仅需计算与 E_ps矩形域内的点的距离,以判断该点是否是核心点,从而可以在很大程度上减少点与点之间距离的计算。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 网格单元 Cell的 Eps矩形域Fig.2 Eps rectangular area of grid unit Cell

基于网格单元的DBSCAN算法首先获取数据集合所在的大区域,然后通过网格划分的方法减少每个点的邻居对象的搜索范围,利用宽度优先搜索,忽略掉低密度的单元,用高密度的区域生成聚类。基于网格单元的DBSCAN算法可以分为以下几个步骤:①将数据空间划分为多个网格单元;②建立数据点到网格单元的映射;③利用宽度优先搜索生成聚类。

点 p邻居对象搜索范围的缩小是在步骤③中体现的,具体步骤如下:

(1)将第一个(下一个)标记为未读的数据点作为种子点送入队列,若所有点都已读,则结束。

(2)如果队列不为空,取队列首部的点进行 E_ps矩形域上的区域查询,并将其标记为已读,如果队列为空,执行第(1)步。

(3)如果 E_ps矩形域内点的个数大于等于Min Pts,则在 E_ps矩形域内检测与种子点之间距离小于等于 E_ps的点的个数是否大于等于Min Pts,如果是,则该点是核心点,将它的 E_ps邻域中的点作为种子点送入队列,如果不是,则将其还原为未读。如果 E_ps矩形域内点的个数小于Min Pts,则直接将该点还原为未读。

(4)循环执行第(2)(3)步。

对于核心点的判断方法,上文已经详细说明,值得一提的是,本算法采用欧氏距离公式计算两个 t维空间点的距离,公式如下:

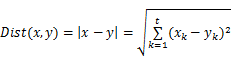
本文所用数据均为二维数据,算法共分为三大步:第一步网格的划分需要计算数据空间上每一维的最大、最小值,时间复杂度为 O( n);第二步进行数据点到网格单元的映射,需要遍历 n组数据,时间复杂度也是 O( n);第三步聚类的生成利用了宽度优先搜索算法,对种子点的考察穿插在宽度优先搜索的过程中,时间复杂度为 O( n+me), m为扩展的种子点的个数, e为当网格单元的边长 L_pg=E_ps/γ时,计算(2 k+1)²个网格内的点数 s并施行相应操作所用的时间,为 O( k²),其中:若 γ≥1, k=γ;若 γ<1, k=1。故整个算法的时间复杂度为 O( n+mk²),可见 m和 k的值越小,时间复杂度越低。

对于数据集合明显呈现一个或多个簇的情况,当 γ<1时, k=1,虽然 k足够小,但是由于网格明显增大, E_ps矩形域内点的个数也将明显增多,显然时间复杂度高于 γ=1的情况。当 γ≥1时, k=γ,此时随着 k值的增大, E_ps矩形域缩小,但是 k²的值会明显增大,具体哪一方面的作用明显,要视簇所呈现的状态而定,一般情况下 k²的增大作用更明显。

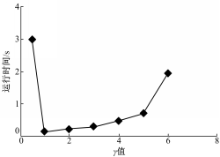
图3是多次对数据量为10 000的数据集合进行聚类时,不同 γ值情况下,运行时间的平均值。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 γ值对运行时间的影响Fig.3 Effect of γ value on running time

根据2.3节的分析和图3所示的实验数据,本文算法选取 γ=1。采用二维仿真数据集合,分别用原始DBSCAN算法和基于网格单元的DBSCAN算法进行聚类分析。算法用Visual Studio 2010实现,实验在一台PC(Intel Core i7 3.4 GHz处理器,8 G内存,500 G硬盘)上完成。参数 E_ps=10,Min Pts=3。

两个算法分别针对同一数据集运行5次并取得运行时间的平均值,在数据量分别为2000、4000、6000的情况下,得到运行时间和准确率如表1所示。

由表1可知,基于网格单元的DBSCAN算法具有较高的准确率和较低的运行时间。

表1

Table 1

表1(Table 1)

表1 两种算法运行时间和准确率对比 Table 1 Comparison of two algorithms on running time and accuracy 数据量 聚类算法 运行时间/s 准确率/% 2000 DBSCAN 0.175449 100 2000 本文算法 0.030928 100 4000 DBSCAN 0.589149 99.8 4000 本文算法 0.068833 100 6000 DBSCAN 1.317306 99.3 6000 本文算法 0.152111 99.6

表1 两种算法运行时间和准确率对比 Table 1 Comparison of two algorithms on running time and accuracy

在数据量分别为2000,4000,…,20 000的情况下,两个算法分别针对同一数据集运行10次并取得运行时间的平均值得到的实验结果如图4所示。由图4可直观看出,对相同规模的数据集,本文算法运行时间明显降低。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 两种算法运行时间对比Fig.4 Comparison of two algorithms on running time