抵抗图像区域攻击的鲁棒性水印算法

引用本文

王友卫, 刘元宁, 朱晓冬. 抵抗图像区域攻击的鲁棒性水印算法. 2014, 44(4): 1151-1158
[WANG You-wei, LIU Yuan-ning, ZHU Xiao-dong. Novel robust watermarking algorithm for regional attacks of digital images. Journal of Jilin University Engineering and Technology Edition, 2014, 44(4): 1151-1158] 复制到剪切板

Permissions

抵抗图像区域攻击的鲁棒性水印算法

王友卫, 刘元宁, 朱晓冬

吉林大学计算机科学与技术学院,长春 130012

通信作者：朱晓冬（1964-）,男,教授.研究方向:虹膜识别,数字水印技术.E-mail:zhuxd@jlu.edu.cn

作者简介：王友卫(1987-),男,博士研究生.研究方向:垃圾邮件过滤,数字图像处理. E-mail:wyw4966198@126.com

基金:国家自然科学基金项目(60971089); 国家重大科技成果转化项目(财建\[2010\]341号);

摘要

为提升算法抵抗数字图像区域攻击能力,提出了一种安全的强鲁棒性数字水印算法。引入随机四元组的概念,使用宿主图像每个随机四元组中的每个8×8小块同时隐藏原始冗余水印及该块的均值信息。水印嵌入前先使用混沌序列对原始水印进行加密,接着结合新的算法性能评价函数寻找最优水印嵌入量化步长上下限;水印嵌入过程中根据图像块内容特性自适应选取最优嵌入量化步长。对比实验表明,随机四元组策略安全性高;算法水印透明性好,在抵抗图像常规区域攻击及其他类型攻击方面显示了较高的鲁棒性。

关键词: 计算机应用; 区域攻击; 随机四元组; 量化步长; 水印透明性; 鲁棒性

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2014)04-1151-08

Novel robust watermarking algorithm for regional attacks of digital images

WANG You-wei, LIU Yuan-ning, ZHU Xiao-dong

College of Computer Science and Technology, Jilin University, Changchun 130012, China

Abstract

To enhance the algorithm's ability of anti-regional attacks of digital images, a secure and highly robust digital watermarking algorithm is proposed. The concept of Random Quaternary Group (RQG) is introduced, and the RQGs of the host image are used to hide the original redundant watermark bits and the mean value of the 8×8 blocks of the RQGs. Before the watermark embedding process, the original watermark is encrypted by chaotic sequence; the performance evaluation function of the proposed algorithm is applied to search the high and low limits of the quantization step of watermark embedding. In watermark embedding process, the algorithm is used to select the optimal quantization step adaptively according to the content of each block. Experiment results show that the RQG strategy is secure; the proposed method has good watermark transparency and high robustness resisting conventional regional attack and other attacks of digital images.

Keyword: computer application; regional attacks; random quaternary group; quantization step; watermark transparency; robustness

Show Figures

0 引言

随着网络技术及数字图像处理技术的飞速发展,因图像非法攻击而带来的图像版权纷争的问题越来越严重。鲁棒性数字水印技术通过向原始图像中附加人眼不可察觉的水印信息保护图像原始版权信息、维护图像所有者合法权益。但是,现有的鲁棒性水印算法大多致力于提升其针对JPEG压缩、滤波、旋转、缩放等攻击的抵抗能力,而真正面向于数字图像裁剪、替换等局部区域攻击的算法却相对较少。文献[3]等从宿主图像水平、垂直两个方向分别循环嵌入水印图像的不同分块,通过调制图像FFT系数大小关系完成水印嵌入过程;文献[4]先对宿主图像进行DWT变换,接着选取LL₁子带系数进行分块DCT变换,最后将水印信息隐藏至DCT系数经过SVD变换后的对角奇异值矩阵中。文献[5]将水印图像分成4部分,通过将每部分重复嵌入至原始图像特定区域中实现水印隐藏,其针对特定形状的区域攻击抵抗力强;文献[6]将8位水印比特依次嵌入到8×8分块DCT低频系数中。算法鲁棒性好,但水印嵌入操作调整了较多低频系数,使得水印透明性不高。

冗余水印嵌入策略是抵抗图像区域攻击的有效方法^{[ 7]},此类方法能在一定条件下降低图像区域攻击对提取水印的影响,但仍存在以下问题^{[ 3, 5, 6]}:①冗余水印比特隐藏块位置生成规则固定,不法者通过只攻击含水印图像特定区域即可达到攻击水印的目的;②隐藏冗余比特的像素块间距离较小,针对特定区域篡改的抵抗能力差;③水印提取过程常需要原始水印参与。为解决上述问题,本文引入了随机四元组的概念,提出了一种基于离散余弦变换(DCT)的自适应图像盲水印算法。

1 随机四元组策略

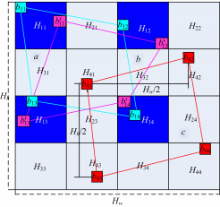
假设宿主图像 H大小为 H_w×H_h,先对 H进行分块,每块为8 ×8大小,接着按图1方式将所得分块集合划分为4 ×4个大小相同的区域{ H_ij}(1≤ i≤4,1≤ j≤4)。可见,区域 H_ij大小为( H_w/4) ×( H_h/4),其每行、每列所含8 ×8大小的像素块数分别为: n_r=H_w/ , n_c=H_h/ 。

	Figure Option View Download New Window
	图1 随机四元组分块策略Fig.1 Random quaternary group blocking policy

针对∀ i∈{1,2,3,4},称{ H_ij}( j=1,2,3,4)构成一个四元域 G_i。

分别从 G_i中的4个区域 H_i₁、 H_i₂、 H_i₃、 H_i₄(1≤ i≤4)中选取块行列坐标分别为( sr_i₁, sc_i₁)、( sr_i₂, sc_i₂)、( sr_i₃, sc_i₃)、( sr_i₄, sc_i₄)的4个8 ×8大小像素块 s_i₁、 s_i₂、 s_i₃、 s_i₄作为水印嵌入起始位置,方法如下:

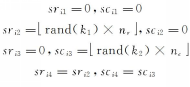
式中:rand( k_i)表示以种子密钥 k_i生成区间[0,1)内的随机数。

定义 s_i₁, s_i₂, s_i₃, s_i₄共同组成一个起始随机四元组,如图1中 a所示。针对 H_i₁中坐标为( r_i₁, c_i₁)( r_i₁≠0或者 c_i₁≠0)的8 ×8大小像素块 b_i₁,按照下面的方法从 H_i₂, H_i₃, H_i₄中求得坐标分别为( r_i₂, c_i₂)、( r_i₃, c_i₃)、( r_i₄, c_i₄)的8 ×8大小像素块 b_i₂、 b_i₃、 b_i₄:

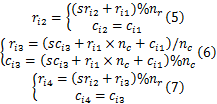
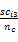
称 b_i₁, b_i₂, b_i₃, b_i₄共同组成一个随机四元组,如图1中 b、 c所示。可见,随机四元组策略结合密钥在 H_i₂, H_i₃区域内随机产生水印嵌入的起始位置,能有效避免不法者在得知冗余水印隐藏规则的情况下,对水印序列的特定位置进行攻击。由式(5)(7)可知,任意时刻随机四元组内 b_i₁与 b_i₂、 b_i₃与 b_i₄间水平方向距离均为 H_w/2;由图1可知,在四元域{ H_ij}中,只有在 r_i₁ =n_r-1或者 r_i₂ =n_r-1的情况下, b_i₁与 b_i₃或者 b_i₂与 b_i₄间的垂直距离才有可能小于 H_w/2,对应发生概率为 p= × 。若取 sc_i₃为均值 n_c/2,则{ H_ij}中某随机四元组满足其中任意相邻小块间距离至少为min( H_w/2, H_h/2)的概率为 p'=1 -p=( n_r-1) /n_r。可见,当 n_r取值较大时,随机四元组策略能较大程度地保证组内任意相邻小块间距离至少为min( H_w/2, H_h/2)。

2 算法描述

算法使用随机四元组隐藏冗余水印并通过投票方式提取水印。为避免从随机四元组中提取的0、1比特数目相等给结果带来分歧,本文向组内每个小块隐藏该块的灰度均值信息。当水印提取过程发生投票分歧时,通过验证组内每个小块的篡改程度来判定最终提取的水印比特。

2.1 水印嵌入过程

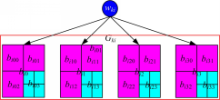
记 l为宿主图像 H中第 k个四元域 G_k内随机四元组数目。如图2中,设 G_ki为 G_k中第 i个随机四元组( k=1,2,3,4;0≤ i<l),{ b_ij}(0≤ j<4)为 G_ki中4个8×8大小像素块。为进一步提升算法安全性,水印嵌入前先使用一维Logistic混沌映射并结合密钥 k₃、 k₄对 W进行加密预处理。Logistic映射初始参数设置为: k₃ =x₀ =0 .2, k₄ =u₀ =1 .55,此时函数进入混沌状态^{[ 8]}。假设当前待嵌入水印比特为 w_ki,则将 w_ki嵌入 G_ki过程如下:

	Figure Option View Download New Window
	图2 本文水印嵌入方法Fig.2 Watermark embedding by proposed method

Step1 根据块 b_ij内容特性自适应确定水印嵌入量化步长 q_ij,首先定义 b_ij对应的灰度 -方差值 S_ij:

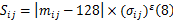
式中: m_ij和 σ_ij分别为 b_ij的灰度均值和方差,分别反映 b_ij的亮度、纹理信息; ε为方差拉伸系数,0 <ε<1。

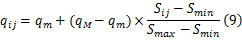
式中: S_min、 S_max分别表示 S_ij值的最小值和最大值; q_m、 q_M分别表示水印嵌入量化步长的最小值和最大值。

Step2 如图2所示,将 b_ij划分成4个4 ×4大小的像素块,分别对 b_ij₀、 b_ij₁、 b_ij₂进行DCT变换,得到直流系数 d_ij₀、 d_ij₁、 d_ij₂,按式(10)分别求得 D_ij、 Z_ij:

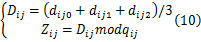
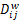
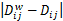
Step3 使用 D_ij隐藏 w_ki,得到。为尽量降低针对图像的修改,这里保证 <0 .5 q_ij。根据 w_ki、 Z_ij对 D_ij做如下调整:

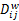
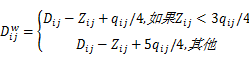
当 w_ki=0时,保证 mod q_ij<0 .5 q_ij,令:

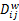
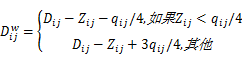
当 w_ki=1时,保证 mod q_ij>0 .5 q_ij,令:

Setp4 按照式(11)对 d_ij₀、 d_ij₁、 d_ij₂进行修正,得到隐藏了水印信息的直流系数、、 :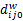

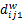
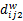
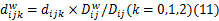
Step5 计算 b_ij灰度均值 avg_ij,将 avg_ij表示成8位二值序列并取其高4位记作{ avg_ij( q)}(0≤ q<4)。

Step6 对 b_ij₃进行2×2大小的分块DCT变换,得直流系数集合{ d_ij₃( q)}(0≤ q<4)。

Step7 取步长 q=q_ij/2,使用Quantization index modulation(QIM)水印嵌入方法^{[ 9]}将{ avg_ij( q)}(0≤ q<4)中每个比特依次嵌入{ d_ij₃( q)}(0≤ q<4)中。

Setp8 逆变换 b_ij中所有子块对应的DCT系数矩阵。

Setp9 遍历{ b_ij}中所有像素块,至此 G_ki中水印隐藏过程结束。

遍历 G_k中所有随机四元组,将 l( l为 G_k内随机四元组数目)个待嵌入水印比特按上述过程隐藏至 G_k中。遍历所有 G_k( k=1,2,3,4)继而完成了图像 H的水印嵌入过程。

2.2 水印提取过程

假设 h'是含水印图像采用Radon方法^{[ 10]}进行旋转校正后的图像,其中第 k个四元域 G'_k内第 i个随机四元组为 G'_ki( k=1,2,3,4;0≤ i<l, l为 G'_k中随机四元组总数),{ b'_ij}( j=0,1,2,3)为 G'_ki中像素块集合,则 G'_ki中所含水印 w'_ki提取过程如下:

Step1 将 b'_ij均分成4 ×4大小像素块集合{ b'_ijp}( p=0,1,2,3),分别对 b'_ij₀、 b'_ij₁、 b'_i₂进行DCT变换,得到直流系数集合 d'_ij₀、 d'_ij₁、 d'_i₂。

Step2 按2.1节中Step1并结合密钥 k₃、 k₄计算 b'_ij对应的水印嵌入量化步长 q'_ij,按式(12)计算 D'_ij, Z'_ij:

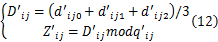
Step3 提取出水印 W'_ij:

若 Z'_ij<0 .5 q'_ij,则 W'_ij=0;否则 w'_ij=1。

Step4 统计{ w'_ij}中0比特的数目 C₀,若 C₀ >2,则 w'_ki=0;若 C₀ =2,转Step5;否则, w'_ki=1。

Step5 对 b'_ij₃进行2×2分块DCT变换,得到直流系数集合{ d'_ij₃( q)}( q=0,1,2,3)。

Step6 取量化步长 q'=q'_ij/2,使用QIM水印提取方法从{ d'_ij₃( q)}中提取水印序列{ w_ij₃( q)},步长为 q'_ij/2。

Step7 将 b'_ij灰度均值转化为二值序列并保留高4位得{ avg_ij( q)}( q=0,1,2,3)。

Step8 获取 G'_ki所含水印信息:

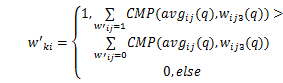
式中: q=0,1,2,3; CMP( avg_ij( q), w_ij₃( q))为比较函数,当 avg_ij( q)与 w_ij₃( q)相等时返回1;否则返回0。

Step9 遍历 h'中全部四元域内全部随机四元组获得提取水印 w_e。

Step10 将2.1节所得Logistic混沌序列与 w_e进行按位与或便得到最终水印 W'。

2.3 水印相似度比较

使用归一化相关(Normalized correlation,NC)方法比较 W'与原始水印 W的相似度,公式如下^{[ 11]}:

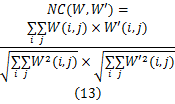
可见, NC( W, W')∈[0,1],其值越大,表示 W'与 W越相似。

3 实验结果与分析

选取512×512大小灰度图像Barbara作为宿主图像,32×32大小的二值图像Girl作为水印图像。

3.1 随机四元组策略安全性分析

若 n_r、 n_c分别为四元域 G中每个区域对应的行、列块数,由于 n_r、 n_c取值相互独立,则在密钥 k₁、 k₂未知的前提下, G中某随机四元组 G_i被选中的概率 P=1 /( n_r×n_c),易知,若攻击者欲改变原始水印序列中对应的 l_w个比特位,则其需对这些比特位对应的 l_w个随机四元组进行篡改,而 l_w个随机四元组全被修改的概率 P_s为: P_s= 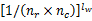。当 n_r=16, n_c=16, l_w=3时, P_s≈5 .941 ×10 ^-⁸,显然,攻击者企图通过穷举法实现对水印序列进行篡改几乎是不可能的。

3.2 含水印图像质量评价

结构相似度(Structural similarity,SSIM)方法^{[ 12]}综合考虑了图像结构、亮度和对比度信息,相对于归一化相关方法^{[ 2]}能更好地反应水印嵌入带来的变化。若原始图像与含水印图像分别用 H、 H'表示,则 SSIM( H, H')定义如下:

SSIM( H, H') =l( H, H') ^α×c( H, H') ^β×s( H, H') ^γ(14)

式中: s( H, H')、 l( H, H')和 c( H, H')分别表示含水印图像的结构、亮度和对比度属性。由文献[12]知,SSIM( H, H')∈[0,1],值越大,含水印图像质量越高。

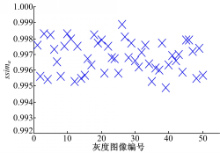
图3显示了 q_m、 q_M取不同值下含水印 Barbara图像及对应的 SSIM值。由图3可见,( a)( b)( c)所示的含水印图像质量良好(对应 SSIM≥0.9987),证明算法满足水印不可见性;图3(d)(e)(对应SSIM≤0.9971)中的图像有较明显的“块状效应”,说明水印嵌入强度过大将影响含水印图像的视觉质量。进一步地,记人眼所能接受的质量差 H'对应SSIM值为 ssim_a,当 q_m取不同值时(为方便计算,令 q_M=q_m+30),分别向编号为0~50的512×512大小的不同灰度图像中嵌入Girl水印。标注每幅灰度图像对应的 ssim_a值,结果如图4所示。可见,不同编号灰度图像对应 ssim_a∈(0 .994,0 .999)。本文将所有图像的 ssim_a均值0 .9969作为人眼所能接收的质量最差的含水印图像,对应SSIM阈值,记为 ssim_th。

	Figure Option View Download New Window
	图3 q_m、 q_M取不同值时所得含水印图像及对应 SSIM值Fig.3 Obtained watermarked images and corresponding SSIM values with different values of q_m and q_M

	Figure Option View Download New Window
	图4 不同灰度宿主图像对应的 ssim_a值Fig.4 ssim_a values of different gray host images

3.3 最优 q_m及 q_M取值

为选取最优 q_m、 q_M,仿真了以下攻击类型: ①1 /4裁剪; ②1 /4替换; ③1 /2裁剪; ④1 /2替换; ⑤3 /4裁剪; ⑥3 /4替换; ⑦质量因子为70的 JPEG压缩操作; ⑧Gauss噪声(均值0,方差5); ⑨3 ×3均值滤波; ⑩锐化(数量100 %,半径1,阈值0)。为了公平,将随机选择裁剪、替换区域所处位置。给定宿主图像 H及含水印图像 H',原始水印 w及提取水印 w',定义算法性能评价函数 F如下:

F=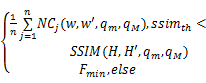(15)

式中: n为 H'遭受的攻击数目; F_min为性能极小值,这里取0.5。选取50幅512×512大小的灰度图像作为宿主图像,在 q_m、 q_M(令 q_M=q_m+q_del( q_del >0))分别取不同值的情况下,将Girl水印嵌入每幅宿主图像中,并计算所有含水印图像在上述攻击下所得 F值的均值,结果如图5所示。由图5可知,最大 F均值为0 .989,对应 q_m、 q_del分别为40、10,故为获得最优算法性能,本文取 q_m=40, q_del =10, q_M=q_m+q_del =50。

	Figure Option View Download New Window
	图5 50幅宿主图像在 q_m、 q_del取不同值情况下算法所得 F均值Fig.5 Average F values of 50 host images under different values of q_m and q_del by proposed method

3.4 算法鲁棒性实验

在常规区域攻击及其他攻击(如:联合攻击^{[ 13]}、JEPG压缩攻击等)类型下测试算法的鲁棒性。为公平起见,保证所有含水印图像SSIM值约为0.9979。

3.4.1 常规区域攻击

图6显示了当含水印Barbara图像遭受不同程度区域攻击时提取出的水印图像,由此可见,虽然含水印图像遭受攻击面积较大,但从中提取的水印图像内容依然清晰可辨,说明算法的鲁棒性能良好。

	Figure Option View Download New Window
	图6 区域攻击后图像及对应提取的水印图像Fig.6 Tempered images with regional attacks and corresponding extracted watermark images

为进一步测试算法的鲁棒性,使用50幅大小为512×512的灰度图像隐藏Girl水印,并计算在区域大小为 l_max× l_max/2(0< l_max H_w, H_h))的裁剪、替换两种攻击下(篡改位置随机确定),不同算法所得 NC均值 nc_c、 nc_r。记 nc'=( nc_c+ nc_r)/2,统计 nc'值如图7所示。由图7可知,未使用冗余水印的文献[4]所得NC值随着攻击面积的逐渐变大而明显变小;文献[3]所得的该结果普遍较本文小,原因在于其针对含水印图像中任意边长为min( H_w, H_h) /2的方形区域进行水印提取,导致提取水印的质量具有随机性;本文方法的结果基本稳定为1,说明本文能更好地抵抗较大程度的常规区域攻击操作。

	Figure Option values obtained by different algorithms under l_max× l_max/2 size regional attacks '>View Download New Window
values obtained by different algorithms under l_max× l_max/2 size regional attacks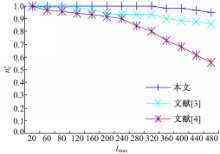 '>	图7 l_max× l_max/2大小区域攻击下不同算法所得 nc'值比较Fig.7 Comparisons of nc' values obtained by different algorithms under l_max× l_max/2 size regional attacks

3.4.2 其他类型攻击

图8中(a)~(d)、(e)~(h)分别为遭受不同程度的联合攻击后的含水印Barbara图像;(i)~(l)、(m)~(p)分别为8(a)~(d)、8(e)~(h)遭受联合攻击后提取的水印图像,并标注了对应的NC值。由图8可知,虽然提取的水印图像中存在不同程度的噪声点,但其中标记信息依然能被准确辨识,说明算法针对所给联合攻击类型表现良好。

实验取50幅大小为512×512的灰度图像嵌入Girl水印。针对每幅含水印图像实施包含不同程度裁剪、替换操作的8种联合攻击,以及不同质量因子(Quality factor,QF)下的JPEG压缩攻击。图9给出了不同算法下所有实验图像所得NC均值。由图9可知,在单纯JPEG压缩攻击下,当QF=50时,本文仍获得较大NC均值(0.9832)且相对其他算法优势明显,这缘于DC系数对JPEG压缩操作的不敏感性^{[ 14]};文献[3]表现最差,这是因为快速傅里叶变换(Fast Fourier transform,FFT)中频系数间大小关系极易受较大程度JPEG压缩攻击的影响。在应对联合攻击方面,当攻击区域较小(含水印图像的1/4)时,本文抵抗包含JPEG压缩、噪声、均值滤波等操作的联合攻击能力较其他算法强,但当遭受包含锐化、对比度增加等操作的联合攻击时,本文表现稍差,这是因为本文使用图像低频系数隐藏水印,而锐化、对比度增加等操作旨在通过弱化图像低频来凸显图像细节即高频部分,因此影响了本文水印提取的效果。当攻击区域为含水印图像的1/2时,文献[3][4]水印误识率下降明显,水印提取精度均不如本文方法。表1依据不同标准将本文与其他算法进行了比较,进一步验证了本文方法作为一种新颖的冗余水印方法在保证算法安全性、提升含水印图像质量及抵抗区域攻击能力方面的应用价值。

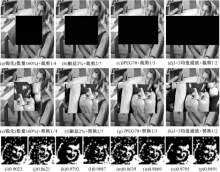	Figure Option View Download New Window
	图8 联合攻击后图像及对应提取的水印图像Fig.8 Tempered images with joint attacks and corresponding extracted watermark images

	Figure Option View Download New Window
	图9 不同攻击类型下不同算法所得NC均值Fig.9 Average NC values obtained by different algorithms under various attacks

表1 不同标准下算法性能比较 Table 1 Performances of different algorithms under different standards

4 结论

(1)使用随机四元组隐藏冗余水印信息,在增强算法安全性的同时降低了含有冗余水印的不同像素块被同时修改的可能性。

(2)向随机四元组中每个小块隐藏该块均值信息,避免了水印提取过程中的投票纠纷。

(3)依据新算法性能评价函数寻找最优水印嵌入量化步长的上下限,在此基础上自适应确定最优量化步长,有效保证了含水印图像的质量。

(4)实验分析表明,算法水印透明性高,随机四元组策略能有效避免攻击者针对水印特定位置进行篡改。

(5)相对于以往方法,本文方法能有效抵抗含水印图像中较大程度的常规区域修改,在应对单纯JPEG压缩攻击及结合了JPEG压缩、缩放、均值滤波等操作的联合攻击方面效果显著。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Lian S, Kanellopoulos D, Ruffo G. Recent advances in multimedia information system security[J]. Slovenian Society Information, 2009, 33(1): 3-24. [本文引用:1]
[2]	Run R S, Horng S J, Lai J L, et al. An improved SVD-based watermarking technique for copyright protection[J]. Expert Systems with Applications, 2012, 39(2): 673-689. [本文引用:1] [JCR: 1.854]
[3]	姜楠, 郝利刚, 朱小陆. 基于二重循环的数字水印算法[J]. 北京工业大学学报, 2012, 38(11): 1694-1697, 1715. Jiang Nan, Hao Li-gang, Zhu Xiao-lu. Digital watermarking algorithm based on dual circulation[J]. Journal of Beijing University of Technology, 2012, 38(11): 1694-1697, 1715. [本文引用:1] [CJCR: 0.3379]
[4]	Zhu S M, Liu J M. A novel adaptive watermarking scheme based on human visual system and particle swarm optimization[J]. Information Security Practice and Experience, Lecture Notes in Computer Science, 2009, 5451: 136-146. [本文引用:1]
[5]	Nasir I, Weng Y, Jiang J M, et al. Multiple spatial watermarking technique in color images signal[J]. Image and Video Processing, 2010, 4(2): 145-154. [本文引用:1] [JCR: 0.409]
[6]	Ahmed N, Al-Gindy H, Ahmad H A. A new blind image watermarking of hand written signatures using low-frequency band DCT coefficients[C]∥IEEE International Conference on Signal Processing and Communications, 2007. [本文引用:1]
[7]	Ammerle-Uhl J H, Koidl C, Uhl A. Multiple blind re-watermarking with quantization-based embedding[C]∥The 18th IEEE International Conference on Image Processing, 2011: 265-268. [本文引用:1]
[8]	胡玉平, 王志坚, 张玲华, 等. 基于小波变换和混沌映射的自适应水印算法[J]. 吉林大学学报: 工学版, 2012, 42(1): 401-404. Hu Yu-ping, Wang Zhi-jian, Zhang Ling-hua, et al. Image-adaptive watermarking algorithm based on chaos map and DWT[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(1): 401-404. [本文引用:1] [CJCR: 0.701]
[9]	Brian C, Gregory W W. Quantization index modulation: a class of provably good methods for digital watermarking and information embedding[J]. IEEE Transaction on Information Theory, 2001, 47(4): 1423-1443. [本文引用:1] [JCR: 2.621]
[10]	罗小刚, 刘静静, 汪德暖, 等. 基于Radon变换与功率谱结合的心脏MR图像配准算法[J]. 计算机科学, 2012, 39(4): 254-257. Luo Xiao-gang, Liu Jing-jing, Wang De-nuan, et al. Cardiac MRI registration algorithm based on radon transform and power spectrum[J]. Computer Science, 2012, 39(4): 254-257. [本文引用:1] [CJCR: 0.61]
[11]	Lai C C. A digital watermarking scheme based on singular value decomposition and tiny genetic algorithm[J]. Digital Signal Processing, 2011, 21: 522-527. [本文引用:1] [JCR: 1.918]
[12]	Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transaction on Image Processing, 2004, 13(4): 600-612. [本文引用:1] [JCR: 3.199]
[13]	王春桃, 倪江群, 卓华硕, 等. 基于可变形多尺度变换的几何不变鲁棒图像水印算法[J]. 自动化学报, 2011, 37(11): 1368-1380. Wang Chun-tao, Ni Jiang-qun, Zhuo Hua-shuo, et al. A geometrically invariant robust image watermarking based on deformable multi-scale transform[J]. Acta Automatica Sinica, 2011, 37(11): 1368-1380. [本文引用:1] [CJCR: 0.572]
[14]	黄继武, Shi Y Q, 程卫东. DCT域图像水印: 嵌入对策和算法[J]. 电子学报, 2000, 28(4): 57-60. Huang Ji-wu, Shi Y Q, Cheng Wei-dong. Image watermarking in DCT: an embedding strategy and algorithm[J]. Acta Electronica Sinica, 2000, 28(4): 57-60. [本文引用:1] [CJCR: 0.686]

2009

0.0

2012

1.854

0.0

. 2012, 39(2):null-null

An improved SVD-based watermarking technique for copyright protection

... 2 含水印图像质量评价结构相似度(Structural similarity,SSIM)方法^[12]综合考虑了图像结构、亮度和对比度信息,相对于归一化相关方法^[2]能更好地反应水印嵌入带来的变化 ...

2012

0.0

0.3379

... 冗余水印嵌入策略是抵抗图像区域攻击的有效方法^[7],此类方法能在一定条件下降低图像区域攻击对提取水印的影响,但仍存在以下问题^[3,5,6]:①冗余水印比特隐藏块位置生成规则固定,不法者通过只攻击含水印图像特定区域即可达到攻击水印的目的 ...

2009

0.0

. 2009, 5451:136-146

A Novel Adaptive Watermarking Scheme Based on Human Visual System and Particle Swarm Optimization

Shaomin Zhu (19) , Jianming Liu (20)

19. China Electric Power Research Institute, 100192, Beijing, China 20. State Grid Information & Telecommunication Co.Ltd, 100761, Beijing, China

In this paper, we proposed a novel watermarking scheme based on adaptive quantization index modulation and singular value decomposition in the hybrid discrete wavelet transform (DWT) and discrete cosine transform (DCT). The secret watermark bits are embedded on the singular values vector of blocks within low frequency subband in host image hybrid DWT-DCT domain. To embed watermark imperceptibly, robustly and securely, we model the adaptive quantization steps by utilizing human visual system (HVS) characteristics and particle swarm optimization (PSO) algorithm. Experimental results demonstrate that the proposed scheme is robust to variety of image processing attacks. In the proposed algorithm the quantized embedding strategy is adopted, so no host image is needed for blind extraction of watermarking image.

2010

0.409

0.0

. 2010, 4(2):145-154 DOI:10.1007/s11760-009-0106-7

Multiple spatial watermarking technique in color images signal

1.University of Bradford School of Informatics Bradford UK

This paper presents a novel multiple digital watermarking technique for the copyright protection of digital color images. In order to improve the robustness against cropping attacks, a binary watermark image is divided into four parts. Each is encrypted by a secret key and embedded into different regions of the blue component of the color image in the spatial domain. Watermark extraction is based on the comparisons between the original intensity pixel values and the corresponding watermarked intensity pixel values in blocks of size 8 × 8. The watermark-extracted bits are determined using the probabilities of detecting bit ‘1’ or bit ‘0’. The watermark can be extracted in several parts depending on the size of the host image, but only four of these are selected by a correlation coefficient detector and used to reconstruct the extracted watermark. Experimental results show that the proposed scheme successfully makes the watermark perceptually invisible and robust for a wide range of attacks, including JPEG-loss compression, median filtering, low pass filtering, rotation, rotation-scaling, rotation-crop, image cropping, image scaling, and self-similarity attacks.

2007

0.0

2011

0.0

2012

0.0

0.701

. 2012, 42(1):401-404

Image-adaptive watermarking algorithm based on chaos map and DWT

Guangdong Province Key Lab of EC Market Application Technology, Guangdong University of Business Studies, Guangzhou 510320, China

A robust watermark algorithm based on discrete wavelet transform and chaos map was proposed. In the algorithm, the watermark was produced by a chaotic sequence and embedded in the lowest band of the original image. Before the watermark was embedded ,a correlation mask for every lowest coefficient was confirmed by the characteristic and tree structure relation of the wavelet coefficients. Then, the hided watermarking strength of every lowest coefficient was controlled by its corresponding mask. The experimental results show that the embedded digital watermarks with this proposed method are image-adaptive, invisible and security, it is more robust.So it is an effective method to protect copyright of digital image.

提出的基于小波变换和混沌映射的自适应图像水印算法中水印由混沌序列生成,在宿主图像的低频系数中嵌入水印信息,嵌入时根据低频逼近系数和高频系数的特点以及树结构关系,给每一个低频系数确定一个相关掩蔽参数,并用此参数控制其对应低频系数嵌入水印时的相对修改强度。实验表明:该算法能够自适应地根据图像内容添加水印,对图像的平滑区进行的修改非常小,而对图像中抑制噪声能力较强的纹理和边缘区域修改较大,使用该算法嵌入的数字水印具有很好的隐蔽性、安全性及鲁棒性。

... 55,此时函数进入混沌状态^[8] ...

2001

2.621

0.0

... Step7 取步长q=q_ij/2,使用Quantization index modulation(QIM)水印嵌入方法^[9]将#cod#x0007b ...

2012

0.0

0.61

... 2 水印提取过程假设h'是含水印图像采用Radon方法^[10]进行旋转校正后的图像,其中第k个四元域G'_k内第i个随机四元组为G'_ki(k=1,2,3,4 ...

2011

1.918

0.0

. 2011, 21:522-527 DOI:10.1016/j.dsp.2011.01.017

A digital watermarking scheme based on singular value decomposition and tiny genetic algorithm

Abstract A robust digital image watermarking scheme based on singular value decomposition (SVD) and a tiny genetic algorithm (Tiny-GA) is proposed in this paper. Previous works have shown that both one-way and non-symmetric properties of SVD make it desirable for watermarking techniques. The produced singular values are very stable and vary very little under various image processing operations or attacks. In the proposed scheme, the singular values of a cover image are modified by multiple scale factors to embed the watermark image. Since the values of scale factors determine the watermark strength; therefore, we use the Tiny-GA to search the proper values in order to improve the visual quality of the watermarked image and the robustness of the watermark. Experimental results demonstrate that our scheme is able to withstand a variety of image processing attacks.

... 3 水印相似度比较使用归一化相关(Normalized correlation,NC)方法比较W'与原始水印W的相似度,公式如下^[11]: ...

2004

3.199

0.0

2011

0.0

0.572

. 2011, 37(11):1368-1380 DOI:10.3724/SP.J.1004.2011.01368

A geometrically invariant robust image watermarking based on deformable multi-scale transform

1. School of Information Science and Technology, Sun Yat-sen University, Guangzhou 510006; 2. College of Informatics, South China Agricultural University, Guangzhou 510642

The robustness against geometrical transforms is still one of major concerns in robust watermarking although significant improvements have been achieved in past decades. This paper tackles the global geometrical attacks by designing a deformable multi-scale transform (DMST) with joint shiftability in position, orientation and scale. Via DMST, we derive theoretically the principles for geometrical synchronization and then utilize it to develop a template-based scheme to efficiently estimate geometrical parameters. The hidden Markov model in the standard wavelet domain is extended to the steerable wavelet domain, which is further used to improve the watermark extraction performance. Experimental simulation demonstrates that the proposed watermarking scheme is quite robust to common signal processing, global geometrical attacks, and their joint attacks.

尽管过去十多年鲁棒数字水印取得了长足的进展,然而如何有效地抵抗几何变换仍然是鲁棒数字水印的关键问题之一. 本文通过设计具有平移不变性、可旋转和可缩放特性的可变形多尺度变换(Deformable multi-scale transform, DMST)来抵抗全局几何攻击. 基于此变换,本文从理论上推导几何同步机制,然后进一步利用它并辅助于模板来设计能有效估计几何攻击参数的算法. 此外,将常规(双)正交小波域隐马尔科夫模型进一步推广到可旋转小波域,以提高水印的检测性能. 实验结果表明本文算法对于常见信号处理攻击、全局几何攻击及其联合攻击具有很好的鲁棒性.

... 4 算法鲁棒性实验在常规区域攻击及其他攻击(如:联合攻击^[13]、JEPG压缩攻击等)类型下测试算法的鲁棒性 ...

2000

0.0

0.686

. 2000, 28(4):57-60

Image watermarking in DCT: an embedding strategy and algorithm

1. Dept.of Electronics,Zhongshan University,Guangzhou 510275,China;2. NLPR,Institute of Automation,Chinese Academy of Science,Beijing 100080,China;3. Dept.of ECE,New Jersey Institute of Technology,Newark,NJ 07102,USA;4. Dept.of Electronics,Chengdu Institute of Meteorology,Chengdu 610041,China

Where should invisible image watermarks be embedded in DCT domain in order for the image watermarks to be invisible and robust?Though many papers in the literature agree that watermarks should be embedded in perceptually significant components,DC components are explicitly excluded from watermark embedding.In this paper,a new embedding strategy and an algorithm applying the strategy for watermarking in DCT domain is proposed.Based on a quantitative analysis on magnitude of DCT components,we argue that more robustness can be achieved if watermarks are embedded in DC components since DC components have much larger perceptual capacity than any AC components.Applying this embedding strategy,an adaptive watermarking algorithm incorporating the feature of visual masking of human vision system is presented.Experimental results demonstrate that the embedding strategy is effective and the invisible watermarks thus generated are very robust.

DCT域的隐形水印应嵌入哪里,水印才足够稳健?尽管许多关于DCT域水印算法的文献赞成水印应放在对视觉效果重要的分量,但DC分量总是被无一例外地排除在外.本文提出了一个DCT域隐形水印的嵌入对策和一个应用该对策的自适应水印算法.基于对图像DCT系数振幅的定量分析,我们指出:DC分量比任何AC分量有更大的感觉容量,从稳健性的角度,DC分量最适合用来嵌入水印.应用这个对策,本文提出了一个把视觉系统纹理掩蔽特性结合到水印编码过程的自适应水印算法.实验结果有效地支持了这个结论,所产生的隐形水印体现了很好的稳健性.

... 9832)且相对其他算法优势明显,这缘于DC系数对JPEG压缩操作的不敏感性^[14] ...