1.初始化门限值 Z₀=0;

2.数据分组 P到达;

3.if 存在 P所属流的记录;

4.更新相应流计数器: c=c+P包含字节数;

5.else;

6.在链表尾部创建新流记录,并置相应计数器为 c=P包含字节数;

7.记 p所属流的估计值 Z=c;

8.if Z≥ Z₀;

9.数据分组 P进入LRU缓存

10.if LRU缓存已满;

11.丢弃LRU底部的流 F₀,根据规则调整过滤门限 Z₀;

12.if P属于LRU中流 F;

13.流 F的字节数 =流 F的字节数 +P包含字节数;

14.将流 F的记录置于LRU的队列顶部;

15.else;

16.建立新流,放置于缓存顶部,相应计数器计为 P₀;

17.else; 丢弃 P;

LRU_based算法最初的目的在于:当有大量小流短期到达时,必然会导致大流被LRU缓存丢弃的情况发生,一旦发生,迅速提高过滤门限,有效地过滤掉包含数据分组较少的小流。该算法是以牺牲少量常态准确率换取大量小流短期出现时的准确率。首先给出两个定义。

定义1:门限时长是指根据淘汰流的大小设置的门限值应该保持的时间。

定义2:门限超时是指门限值的实际保持时间超过了门限时长。

门限时长 T应随着淘汰流 M变大而增大,即 T( M)为增函数,即 T(1) <T(2) <… <T( n) <T( n+1) <…。为方便计算,此处设定 T和 M成正比例关系,即满足 T=KM( K为常系数),则 T( n) =nT(1)。

类似地,门限值与淘汰流之间的关系也为增函数,同样设置为正比例关系,即门限值 Q=LM( L为常系数)。设置门限后,如果下一时刻丢弃的流更大,说明当前门限值还不够大,应该提高门限;如果丢弃的流变小,证明设置门限有效,属正常情况,则维持当前门限不变,等待当前门限时长结束。实现流程如图2所示,其中 T₀为根据门限值 Z₀设置的门限时长。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 时长设置流程图Fig.2 Flow chart of duration setup

数据分组进入流归并缓存和LRU缓存时,首先查找相应的流记录,本文均采用Hash方案,其计算复杂度均为 O(1)。随后的操作包括LRU缓存中流记录在双向链表中的移动,流记录的移动是有限常数次指针操作,其计算复杂度为 O(1),因此,LRU_based算法处理一个数据分组的时间复杂度为 O(1)。

流归并缓存部分,假设 b为分组平均大小; R为链路速率, n为每流平均分组数,则在时间 t内到达流测速缓存的流个数,也即流归并缓存的空间为:

LRU缓存部分,由于每个大流所占链路总容量的比例为 P,所以最多会有1 /P个大流,故LRU缓存的空间复杂度为 O(1 /P)。

处理一个数据分组需要访问存储器的次数是衡量一个算法效率的关键因素之一。在LRU方法中,表项采用双向链表结构组织,当有新的数据分组到达时,首先查找LRU缓存中是否有相应的流记录,分两种情况:①不存在相应的流记录,新建流记录;②存在流记录,对其更新,分别需要访问内存4次(如果新建流记录后,LRU缓存已满,则将最后一个表项丢弃,需访问内存1次,此时共需访问5次)和6次。LRU算法访问存储器次数如下:首先,在LRU缓存中查找流记录分两种情况,若 F属LRU:查找记录(1次);修改流目录(4次);修改指针(1次),共6次;若 F不属LRU:查找记录(1次);创建流目录(1次);修改第一个指针(2次),共4次。

本文方法和LRU方法相比,在内存访问次数上,增加了流归并缓存中的处理过程。

在流归并环节,由于采用单向链表结构。数据分组访问内存的次数最少的情况为:数据分组进入流归并缓存,查找相应流记录;找到并修改流记录;当该数据分组所属流小于当前门限值时,被丢弃,这种情况下,处理该数据分组需要访问内存2次。

当数据分组进入流归并缓存,查找;没有找到相应的流记录,此时需创建新的流记录;修改指针,共需要访问内存3次。即在流归并阶段,最多需访问内存3次,最少2次。

结合上述LRU缓存访问次数的分析,LRU_based方法处理一个数据分组最多需访问存储器(3+6)次,最少为2次。

表1为LRU_based算法与Sample and Hold算法、Multistage Filters算法^{[ 8]}和LRU算法访问存储器的次数比较。

根据以上分析,算法最多需要9次访问内存操作。根据当前的硬件性能,SRAM访问速度可以达到2~5 ns,假设使用3 ns的SRAM,则最坏情况下,算法需要27 ns处理一个数据分组。当有大流被淘汰时,门限值提高,使得大量属于小流的数据分组不能进入LRU缓存,进一步降低了平均内存访问次数,提高了算法的处理速率。互联网中封装TCP协议的IP分组最小长度为40字节,10 GB链路中,满负荷状态下每个分组的处理时间为32 ns。因此,算法的处理速度理论上完全可以满足10 Gbit/s链路的要求。

表1

Table 1

表1(Table 1)

表1 不同算法访问存储器次数比较表 Table 1 Number of different algorithms access memory table 算法 最少访问次数 最多访问次数 本文算法 2 9 MF lg n 1+lg n SAH 1 1 LRU 4 6

表1 不同算法访问存储器次数比较表 Table 1 Number of different algorithms access memory table

设流归并缓存大小为 L₀,LRU缓存大小为 L₁,每隔 t时间对归并缓存的计数器进行清零处理。单位时间段内通过链路的流个数平均为 S,则在 t时间段内进入流归并缓存的流数量可近似为 tS,则所需流归并缓存的大小为 L₀ =tS。即所需流缓存的大小和时间 t成正比,因此, t越小越好;另一方面, t又不能太小,以至于失去流归并的功能。经过试验验证,此处取 t=1 s最合适。

为使各种算法测量效果的展示更为直观,首先对oc48-mfn的前5 s数据,采用不同的算法进行大流检测,将检测出的大流从大到小排序,如图3所示。

在前5 s时间内,oc48-mfn测试数据流的总数为45 382个,大流的数量为104,如图3(a)所示;对于LRU算法,检测得到的大流数为91;如图3(b)所示,丢掉了数值较大的几个大流点;对于MF算法,计算得到的大流数目为107,如图3(c)所示;MF算法检测出的大流数量多于实际大流数目,原因是MF使用Hash函数存在将多条流映射到同一个入口,多条小流相加检测为大流的情况;对于SAH算法,设置抽样率为0.000 04,计算得到的大流数目为82;对于本文算法,反馈函数采用正比例函数,经过多次试验,发现当取 L=0 .3、 K=2时效果较好,计算得到的大流数目为101。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 大流检测算法效果比较Fig.3 Algorithms comparison

将总的测量时间300 s分为 J段,每5 s为一测量时间段,假设第 j个测量时间段内共有大流 M_j个,其中大小分别为 N_i字节,使用本文算法检测的相应的流大小为 T_i( i≤ M_j),漏检的大流个数为 O_j,误检的大流个数为 Q_j,采用3个尺度衡量算法的准确性:

平均假阴性误判率(AFNR):

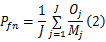
平均假阳性误判率(AFPR):

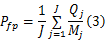
第 j个时间段相对误差率:

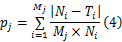
故整个测量时间平均相对误差率(ARER):

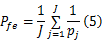
经过试验比较,得到的结果如表2所示。

表2

Table 2

表2(Table 2)

表2 算法准确性比较 Table 2 Comparison of algorithm accuracy % 评价指标 Pfn Pfp Pfe LRU_based 2.3 0 0.33 LRU 12.5 0 0.57 MF 0 2.54 1.42 SAH 13.1 0 0.84

表2 算法准确性比较 Table 2 Comparison of algorithm accuracy %

Sample and Hold算法由于只需访问一次存储器,效率较高且容易实现,但假阴性误判率较高,很多大流不能被检测到;Multistage Filters算法不存在假阴性误判,但假阳性误判率较高,处理速度慢、实现难度大;本文算法相对于Sample and Hold算法更准确;相对于Multistage Filters算法速度更快。因此,本文算法满足工程应用所需的实现简单、处理速度高、准确性较高的要求。