作者简介:贺岩(1980-),男,博士研究生.研究方向:信号处理.E-mail:yanhe08@mails.jlu.edu.cn
利用信道相关估计、压缩采样以及基追踪的信号重构理论,并应用平均一致算法实现了多用户合作检测。在瑞利衰落信道环境中,将本文算法与传统能量检测算法进行了仿真比较。仿真结果表明:与传统能量检测算法相比,本文算法在较低信噪比环境中,使用较少的采样数量即可获得较好的检测性能;同时,当认知用户增加时,检测性能也有所提高。
Using correlated channel estimation, compressive sampling theory, signal reconstruction based on the basis pursuit technique and the average-consensus algorithm, the proposed algorithm realizes effective and accurate signal detection. The proposed algorithm is compared with the traditional energy detection scheme in the condition of Rayleigh fading. Results show that the proposed algorithm can achieve better performance than the energy detection scheme in low SNR and less sampling rate scenario. Meanwhile, the detection performance can also be improved when the cognitive radio users increase.
随着无线通信业务的迅猛发展,无线频谱资源日益稀缺,然而现有的频谱分配制度使频谱资源没有得到充分有效的利用,根据美国联邦通讯委员会(FCC)在2003年的调查统计,现阶段的频谱资源利用率为15%~85%[ 1]。解决当今频谱稀缺问题成为近年来学者研究的一项重要课题,一些研究人员把频谱利用率更高的动态频谱接入方式作为解决方案进行研究,1999年认知无线电(Cognitive radio,CR)由Mitola等[ 2]首次提出以来得到研究人员的广泛关注,作为频谱资源有效利用的解决方案[ 3],其主要思想是非授权用户在不影响授权用户正常通信的前提下通过动态频谱接入方式合理使用空闲频谱,从而提高频谱的利用效率,解决频谱稀缺问题。
传统采样过程必须满足香农采样定理,即采样频率不能低于信号最低频率的2倍,2006年Candes等[ 4]从数学上证明了从不完全的傅立叶变换系数中精确重构出原始信号,为信号的压缩采样奠定了理论基础[ 5],同年Donoho[ 6]提出压缩感知(Compressed sensing,CS)理论,从此对于稀疏信号的采样可以摆脱香农采样定理的束缚,以远低于奈奎斯特采样频率对稀疏信号进行采样,得到的压缩信号用最小 l0范数的优化算法精确重构出原始信号,从而提高采样速度,以较少的采样点数获得高频宽带稀疏信号重要信息,在一定程度上降低了系统的软硬件复杂度,显著提高了信号处理效率。压缩感知被提出以来便得到科研人员的广泛关注,并成为研究热点,其中也有一些学者把压缩感知技术引入到频谱感知的研究领域,文献[7]将压缩感知理论应用到认知无线网络中的宽带信号的频谱感知中,基于压缩感知重构原始信号的频谱估计,利用小波边缘检测器对频谱边缘进行检测,该算法在较低信噪比的衰退信道环境中不能得到较好的检测概率。文献[8-9]利用模拟信息采样理论获取宽带模拟信号,以低采样率信号对其功率谱进行估计,文献[10]对其进行扩展,应用到分布式CR网络进行研究。文献[11]基于压缩感知理论利用宽带信道的稀疏性结构估计其功率谱密度实现对宽带信道的感知,文献[12]用传统的MVDR(Minimum variance distortionless response)算法对由压缩采样信号重构出的原信号进行频谱感知。
在众多基于压缩感知理论的频谱检测文献中,少有文献解决宽带频谱检测问题,本文结合压缩采样理论[ 13, 14]、信道估计技术、信号重构理论以及平均一致融合算法提出一种有效的宽带多用户频谱感知算法。把宽带信道分成若干个互不重叠的子信道,利用信道参数的相关特性对信道进行估计,基于压缩重构理论对原信号进行恢复,获得检测统计量,与给定的门限比较得到单用户检测结果,最终应用平均一致算法融合各感知用户的检测结果获得空间多样性增益来提高系统性能。最后,在瑞利环境中对本文算法进行仿真实验,仿真结果显示,本文算法在较低的采样速率下也能得到良好的检测性能,同时随着感知用户数量的增加检测性能也随之提高。
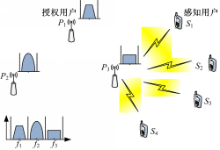
考虑一个由授权用户和感知用户共同组成的宽带信道,将整个宽带信道分成 M个带宽相等且互不重叠的窄带子信道,每个子信道的中心频率为 fm且已知,其中 m=0,1,…, M-1。信道的功率大小会随着授权用户的存在与否而实时变化,而那些频谱空闲的子信道可以为感知用户提供频谱进入的机会。假设系统中有 J个空间分布的感知用户合作检测整个宽带信道上的频谱空洞。同时,假设有 I个授权用户在检测期间活动,则 I个授权用户传输的信号记为 si( t),其中 i=1,2,…, I。
如图1所示,第 i个授权用户信号 si( t)通过无线传输信道到第 j个感知用户接收机后的信号可以表示成 hij( t) *si( t),其中 *表示卷积计算, hij( t)表示从第 i个授权用户到第 j个感知用户之间的信道脉冲响应,假设信道在检测期间是缓慢变化的时不变信道。因此,第 j个感知用户的接收信号可以表示为:

为了避免干扰,认为授权用户数量不大于可用子信道数量, wj( t)表示均值为零、方差为 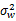
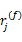
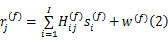
式中: 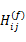
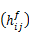
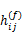
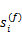
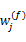
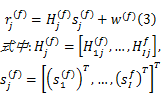
为了更好地检测频谱空洞,每个感知用户需要从接收信号 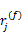
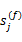
本文利用已知的训练序列对信道进行估计,假设信道参数在时频域具有相关性,感知用户已知授权用户使用的训练序列码(Training sequence code,TSC),在时间 t第 j个感知用户收到的训练序列码表示为:
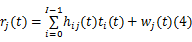
式中: hij( t)可以表示为一组时间有限的脉冲序列:
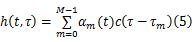
式中: αm是第 m条路径的广义平稳窄带复高斯振幅,不同路径间彼此独立; c( t)是整形脉冲函数; τm表示第 m条路径的时延;信道在时间 t的频域响应为:
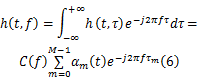
式中: C 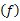
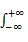
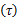
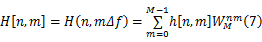
式中: h 
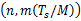
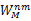
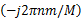
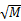

式中: Hij 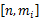
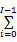
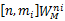
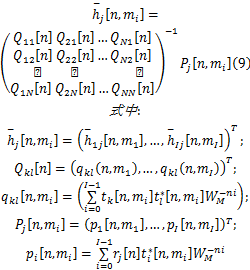
本算法由两部分组成,首先利用压缩采样技术在时频域检测频谱,然后利用融合算法在空间域进行合作检测。为实现该算法,先对单个感知用户压缩检测算法进行研究,利用式(3)中信道的估计参数 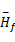
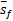
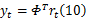
式中: rt是 M×1维离散时间信号; Φ是 M×K( K<M)维投影矩阵,其列向量 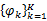

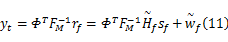
式中: 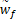
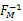
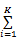
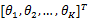

对每一个感知用户接收机,判决统计向量 T( j)可以通过比较给定的判决门限得到:
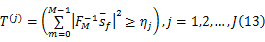
式中:检测门限 ηj可以基于一个给定的错误报警概率 Pfa来获得,在 H0假设条件下,接收信号由噪声组成,其概率密度服从均值为零、方差为 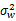
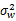
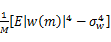
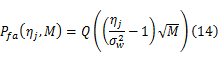
式中: Q 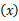
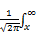

在 H1假设条件下,判决统计量 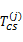

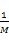
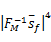

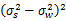

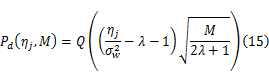
式中: λ= 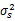
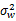
在实际应用中,由于无线信道的多径效应,信号的传输会产生衰落,当接收信号的振幅服从瑞利分布时,接收信噪比 λRAY的概率密度函数服从指数分布:
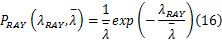
式中: 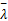
给定一个检测门限 ηRAY,瑞利衰落信道的错误警报概率为:
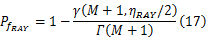
式中: γ 
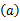
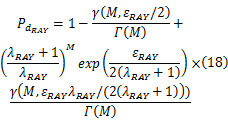
为了提高频谱检测性能,本文利用多用户合作频谱感知方案收集空间多样性增益,允许不同的感知用户彼此共享他们的检测信息,为了减小感知用户间传递信息的信道开支,考虑硬判决融合方案,感知用户彼此传递本地判决状态给其他感知用户。本文采用平均一致算法[ 17]实现合作频谱检测。假设各感知用户间为理想信道,对于整个感知网络,合作检测的判决均值为 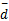
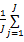
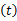
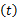

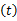
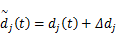
式中: Δdj= 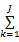
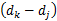
每个感知用户将合作判决与给定的门限 ηc进行比较得到最终判决结果。不同的门限设置决定不同的感知用户频谱进入机会,在最保守的认知网络中,当任何一个感知用户检测出授权用户存在时,其网络最终判决授权用户存在的门限值为 ηc=1 /J,而更激进的网络认为:当超过一半的感知用户判决为1时,网络最终判决授权用户存在的门限为 ηc=1 /2。
本文实验考虑一段含有16个子信道的宽频带,授权用户随机占用其中子信道,假定占用率为20%,授权用户信号采用线性频率调制信号,为获得精确的授权用户信号,信号的采样间隔 τ=200 μs,采样频率约等于3倍信号带宽,采样点数500。授权用户信号在波形匹配字典 Ψ上的投影具有稀疏性,令 τAIC表示模信转换(AIC)的采样间隔,定义参数压缩比 r=τ/τAIC来评估本文算法性能,例如压缩比 r=0 .1表示AIC的采样频率是奈奎斯特采样频率的1/10。宽带信道经历频率选择性衰落,参考模型采用多径瑞利衰落环境。
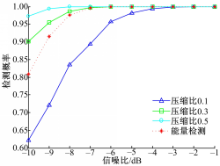
图2给出了在高斯白噪声中本文算法与传统能量检测算法的性能比较,实验给出了在不同信噪比以及压缩比下的两种算法的检测概率,两种算法均在错误警报概率为0.1的条件下进行仿真实验。传统能量检测的采样频率为5000 Hz,其在信噪比为(-10,-1) dB条件下的检测概率如虚线所示。从图中可看出,本文算法检测概率在压缩比分别为0.3和0.5两种情况下优于传统能量检测算法,在压缩比为0.1的情况下检测性能有较大幅度下降,检测概率低于传统能量检测算法。
在实际通信环境中,接收信号受多径效应影响,信号能量出现衰落,在瑞利衰落环境中对本文算法进行仿真实验。假设授权用户信号经由3条路径到达感知用户接收机,时延分别为100、200、300 μs,多谱勒频移为20 Hz。
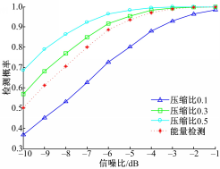
图3给出了本文算法在瑞利衰落环境中压缩比分别为0.1、0.3、0.5时不同信噪比下的检测概率以及与传统能量检测算法的性能比较。从图3可知,在瑞利信道环境中,以压缩比大于0.3的采样频率采样,本文算法仍然优于传统能量检测算法,并且在-6 dB信噪比环境中的检测概率仍然大于0.9。
通过对本文算法的仿真实验可知:授权用户信号经过压缩采样后的观测向量的信噪比有所增加,图4给出了观测向量的信噪比增益随着压缩比的变化情况,分别在三种信噪比下对本文算法进行了仿真。由4图中可以看出,观测向量的信噪比增益几乎不受授权用户信号的信噪比影响,性能曲线随着压缩比的增大而下降。这是由于随着压缩比的减小,观测向量中的授权用户信息在观测向量中所占的比重增加,以至于观测向量的信噪比增加,同时信噪比增益增加。
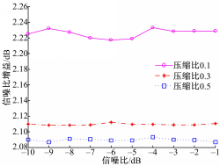
图5为在不同信噪比和压缩比条件下的信噪比增益的变化曲线,从图5中可以进一步看出,本文检测算法的信噪比增益几乎不随授权用户的信噪比变化而大幅波动,压缩比越小,信噪比增益越大。由此可见,该算法的压缩采样信噪增益对授权用户的信噪比具有一定的鲁棒性。
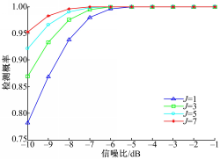
从图6可以看出,随着感知用户的增加,检测性能也随之提高,仿真实验是在误警概率为0.1、压缩比为0.2的条件下进行的,当压缩比提高时,检测性能也随之提高,同时会增加系统的采样负担,检测时间也会随之增加。
本文提出了一种基于压缩采样、信道估计以及基于压缩感知理论重构信号的频谱感知算法,结合平均一致算法对各感知用户的检测结果进行融合,得到最终的检测统计量。与传统的检测算法相比,本文算法的采样频率不受奈奎斯特理论限制,在一定程度上减轻了系统计算负担。仿真实验结果表明,在采样频率减小的情况下,本算法的检测性能仍比传统能量检测算法有所提高,同时随着感知用户的增加,检测性能也随之提高。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|