作者简介:行鸿彦(1962-),男,教授,博士.研究方向:微弱信号检测与处理,仪器仪表设计. E-mail:xinghy@nuist.edu.cn
在混沌预测模型基础上,提出了消散型同步的混沌背景下微弱信号检测算法。采用径向基函数神经网络(RBFNN)拟合混沌模型,结合消散型同步实现混沌时间序列与混沌系统的同步,利用同步误差实现微弱信号的检测。以Rossler混沌系统为研究对象,验证了算法的可行性,研究了噪声对微弱信号检测的影响。仿真研究表明,该算法能检测各种频率的微弱信号,在一定条件下可检测到信杂比大于-110 dB的微弱周期信号;若信噪比
Based on the chaos forecasting model, a dissipative coupling detection method is proposed for detecting weak signal in chaotic background. The Radial Basis Function Neural Network (RBFNN) is applied to fit the chaos forecasting model. The synchronization between chaotic time series and chaos system is realized by combination of RBFNN and dissipative coupling. Then the synchronization error is used to detect the weak signal. The Rossler chaos system is taken as the object to test the feasibility of the proposed method and analyze its performance with weak signals of different frequencies. In order to avoid the mixed impact of noise and chaos time series to the performance of the method, the interference of noise intensity on weak signal detection is investigated in depth. Simulation results show that the proposed method can detect weak signal with different frequencies; under certain conditions, the method can detect weak periodic signal if the Signal-to-Clutter Ratio is bigger than -110 dB. The noise influence on the detection performance can be ignored if the Signal-to-Noise Ratio (
混沌[ 1]是非线性的确知系统,具有对初始条件极其敏感、短时可预测等特性,混沌背景下的微弱信号检测与估计是目前信号处理研究的热点和难点。混沌背景下微弱信号检测的主要理论依据是混沌相空间重构和神经网络理论,其实质是选择合适的方法抑制混沌序列,突显微弱信号,实现微弱信号检测。首先,采用伪最近邻法[ 2, 3]、C-C法[ 4]、互信息量[ 5]等获得混沌时间序列的嵌入维 m和时间延迟 τ,重构混沌相空间;然后运用神经网络拟合混沌预测模型;最后,利用混沌预测模型进行单步预测,获得预测值,并计算预测值与实际值的误差,运用适当的方法(傅里叶变换FFT、幅值分析等)检测误差中是否存在微弱信号。1995年,Haykin[ 6]等采用反向传播(BP)神经网络与混沌相空间重构结合,较好地解决了海杂波(具有混沌特性)背景下的微弱信号检测。随后研究者提出了混沌相空间重构与径向基函数(RBF)[ 7, 8]、支持向量机(SVM)等[ 9]神经网络结合的改进算法。但这类方法也存在一些问题:①没有讨论噪声对检测的影响,只有少量文献对噪声进行了[ 10]研究,而实际应用中,噪声无处不在,导致方法的实用性降低;②忽略了微弱信号对混沌系统后期状态的影响,而当周期信号加入到混沌时间序列中时,这种影响不能忽略。
Kurian等[ 11, 12, 13]通过添加对偶同步改进了上述方法,在分析过程中考虑了噪声的影响,提高了方法的实用性,引入同步后算法在性能上有了较大提高[ 12]。混沌同步减小了噪声、微弱信号对混沌系统后期状态的影响,但文献[11-13]中只分析了算法在较高信杂比(-25 dB)下的检测性能,没有分析在低信杂比下的检测性能及噪声的影响。混沌同步一般是指两个混沌系统最终到达同步的过程,混沌对初始条件非常敏感,两个混沌系统看似不可能同步。1990年,Pecora和Carroll[ 14]发现了两个耦合混沌振子的同步现象,提出了PC同步法使混沌应用成为可能[ 15, 16]。混沌同步减少了初始条件对混沌系统的影响,可用于含噪声混沌系统的参数估计[ 17, 18]。1994年,Brown[ 19]提出采用混沌时间序列建模实现系统的混沌同步,2002年,Voss[ 20]提出消散型混沌同步实现了混沌时间序列与混沌系统同步。采用混沌时间序列与混沌系统的同步实现微弱信号检测具有可行性。混沌同步的研究也得到了国内学者[ 21, 22]的关注。
近年来,作者对混沌背景下的微弱信号检测进行了一定的研究[ 9],但这些方法只研究了混沌信号和微弱信号存在的情况,没有考虑噪声的影响。本文将在上述研究基础上,结合混沌同步理论,实现混沌信号、噪声、微弱信号同时存在的微弱信号检测,使检测方法的实用性更强。
驱动-响应模型是混沌同步中较成熟的模型,单向耦合混沌同步[ 23]是驱动-响应同步中的一种,其定义如下。
假设某混沌系统表示为:
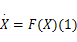
则由该系统作为驱动系统和响应系统组成的单向耦合的动力学方程组为:

式中: E为一个矩阵,它是确定响应系统与驱动系统变量差的线性组合; a为耦合强度或者回馈系数,其中 e=X-Y称之为误差系统,当 e趋向于0时,称系统实现完全的单向耦合同步;驱动系统为 F( X),响应系统为 F( Y, X)。
通常混沌同步是指两个混沌系统同步,2003年Voss[ 20]提出了消散型耦合同步,实现了混沌时间序列与混沌系统的同步,这种实现扩大了混沌同步的运用范围。混沌时间序列 xn可看作 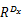
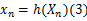
如果将 xn作为驱动系统的输出,那么离散响应系统表示为:
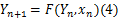
式中: Yn是 n时刻的混沌状态; Yn+1是 n+1时刻的混沌状态。
选择合适的参数即可实现混沌时间序列与响应系统的单向耦合同步。
假设存在混沌时间序列 xn( n=1,2,…, N),可采用多种方法找到同步响应系统,其中最常用的方法是首先采用相空间重构和神经网络等技术拟合混沌预测模型。然后依据预测模型建立混沌系统模型,最后确定响应系统。
首先,依据对混沌时间序列采用时间延迟法重构相空间,其中:
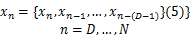
式中: D表示嵌入维。
然后,采用BP、RBF或SVM神经网络拟合混沌预测模型:
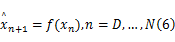
采用混沌预测模型 f( x)建立混沌系统如式(7)所示。
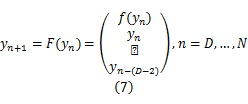
而混沌系统的输出 yn+1 =f( yn)=h(F( yn)),即混沌状态的第一个分量。
消散型耦合混沌同步的响应系统形式[ 20]如下:

式中: yn是混沌系统 F( y)在 n时刻的状态; xn是输入的混沌时间序列; yn是同步系统的输出。
由式(8)可知,消散型混沌同步是通过耦合参数 K使输入 xn与同步系统输出 yn之间的差值逐渐减小,最终实现混沌同步。
耦合参数 K可通过混沌时间序列 x(驱动信号)与响应系统的输出 y(响应信号)的相关系数[ 20]或误差的最小均方差[ 12]来确定。 x、 y的相关系数越接近1,说明两个信号越相似,等于1时达到完全同步,因此 x与 y相关系数为最大值时对应的 K即为同步参数 K;当 x和 y的误差的最小均方差达到最小值时,说明此时 x与 y的同步性最好,此时的 K即为耦合参数 K,也可称为同步参数。
假设实际需要处理的信号如式(9)所示:

式中: cn为混沌背景; sn为需要检测的微弱信号; ηn为白噪声。
传统检测算法中为了简化模型,忽略 ηn。为提高检测算法的实用性能,本文不简化模型。
混沌背景下的微弱信号检测主要分为三个步骤:
步骤1 对不含微弱信号的混沌信号 cn确定嵌入维 m和时间延迟 τ,完成混沌相空间重构。其中 cn= 
步骤2 运用神经网络拟合混沌预测模型 f( x)。通常选择BP、RBF、SVM等神经网络。本文选择RBF神经网络,RBF理论上具有能实现任意函数的模拟,避免局部极小值问题,结构简单等优点。高斯基函数是RBF神经网络中的经典基函数,采用该基函数具有普遍性。
RBF神经网络的表达式为:
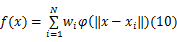
式中: wi是权重; x为输入; φ(‖ x-xi‖)=exp( 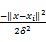
本文在上述基础上添加消散型同步[ 20],混沌同步减少了初始条件对预测混沌系统的影响,考虑了微弱信号与噪声对预测混沌系统的影响,提高了系统的实用性,其中消散型耦合同步系统的输出如式(11)所示:
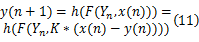
式中: K为耦合参数; F( Y)为混沌系统; F( Y)由混沌预测模型 f( y)构建,如式(7)所示, Yn为混沌系统 n时刻的状态, Yn={ y( n), y( n-1),…, y( n-D+1)}T, x=h( x)是混沌向量在混沌时间序列的映射。当存在某一时刻 N1,满足 x( n) -y( n) =0, n≥ N1,此时序列 x( n)与 F( x)完全同步。若 x中包含噪声和微弱信号, x与混沌 F( Y)系统将不能完全同步,即同步误差 x( n) -y( n)≠0,噪声和微弱信号的特征会保留在同步误差中,可使用该同步差别 x( n) -y( n)实现微弱信号的检测,因此实际处理的对象为 err( n),如式(12)所示:
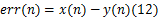
步骤3 微弱信号的检测。混沌背景下的噪声和信号的特征就会保留在同步误差 x( n) -y( n)中,因此对误差 err( n)进行相应的处理就能实现微弱信号的检测。

由式(13)可知,通过同步系统处理后的同步误差主要包含噪声和微弱信号,实质上是将混沌背景下的微弱信号检测问题转化为从同步误差中检测微弱信号的问题。通过消散型同步抑制混沌时间序列,突显微弱信号。若存在微弱周期信号,则采用FFT处理对 err( n)进行频谱分析,观察频谱图对应频率处是否存在突起等特征。如果存在瞬态信号,则可直接对误差值进行幅值分析,但并不仅限于频谱、幅度分析,还可以采用自相关、多重相关、双谱估计等微弱信号检测理论。但是即使同步系统参数非常精确,误差中仍会存在残余混沌信号,当微弱信号非常小,特别是当残余混沌信号和噪声、微弱信号在同一数量级时,微弱信号将不能被检测,本方法检测微弱信号的性能在3.4节进行分析和讨论。
为验证方法的有效性,采用经典Rossler混沌系统[ 23](如式(14))作为实验对象。
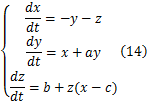
式中: a=0 .15; b=0 .2; c=10。
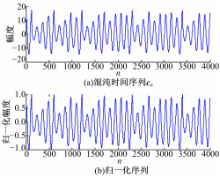
积分步长为0.05 s,选择状态 x作为混沌时间序列,积分步长可作为实际中的采样时间间隔,取4000点混沌时间序列作为混沌背景,记作 cn, n=1,2,…,4000,如图1(a)所示。为了说明方法的通用性,依托南京恒立达光电仪器厂的MKS-CEC-Ⅲ新型混沌演化控制实验仪进行实验,该实验仪能产生Coullet混沌[ 24]。采集Coullet混沌的状态 x作为实验数据进行方法的通用性分析。本文假设需要检测的微弱信号为周期信号,采用正弦信号作为检测目标。
为了量化分析噪声、混沌杂波对微弱信号检测性能的影响,避免噪声与混沌杂波对检测影响的混叠,引入信噪比( SNR)和信杂比( SCR):
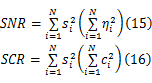
在分析过程中加入适当的白噪声成分,讨论随着 SNR的变化,算法检测微弱信号的性能的变化情况,分析噪声对信号检测的影响。
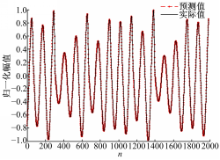
将混沌背景 cn采用最大最小归一化方式归一化到(-1,1),如图1(b)所示。取前2000点作为训练样本,后2000点作为测试样本,确定单步混沌预测模型,选择时间延迟 τ=1,嵌入窗 D=15,该值并不唯一,经实验验证当 D≥10时,可获得较好的实验效果。采用RBF神经网络拟合出单步预测模型,为了避免过拟合等问题,训练误差可设置在1×10-10左右。图2是采用RBF网络拟合的预测模型效果图,由图可知该预测模型拟合效果好。
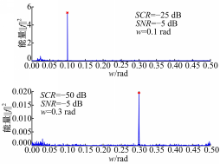
在已知的混沌信号 cn中添加 SCR=-25 dB, SNR=-5 dB的白噪声和正弦信号,周期信号频率 w=0.2 rad,正弦信号相对混沌信号可视为微弱信号。对混合信号进行最大最小值归一化操作,取后2000点作为驱动信号。运用同步系统输入输出的误差的均方差值确定同步参数 K,输入输出误差的均方差越小,说明同步性能越好。对于一系列的 k,如果同步系统输入输出的误差存在极小值点,则该极小值点对应的 k即可作为同步参数 K。通常对不同的输入信号,同步参数存在一定的差别,必要时可采用训练集合中的输入输出集合进行训练,选择合适的初始参数 k(1或者0),比较同步系统的输出与实际的输出集,采用LMS算法确定合适的同步参数 K实现自适应处理,但同一 SCR情况下,可认为同步参数是近似相同的。如图3所示,当 K=0 .61时,误差值的均方差值图中存在局部极小值,因此可认为采用 SCR=-25 dB, SNR=-5 dB的混合信号驱动同步系统的同步参数 K=0 .61。
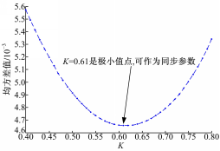 | 图3 基于最小均方差极小值的同步参数确定Fig.3 Synchronization parameter determined based on minimal value of mean square error |
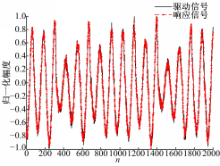
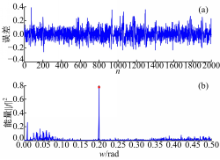
同步系统可用来实现微弱信号的检测,图4是添加了微弱周期信号和噪声的驱动信号和采用驱动信号驱动同步系统的输出信号(响应信号),可知两种信号基本重合,这说明系统实现了混沌时间序列与混沌系统的同步,但两种信号也存在一定的差别。图5(a)是驱动信号与响应信号的误差,该误差类似于噪声,没有明显的周期特性,也没有图4的混沌信号特征,说明混沌同步较好地抑制了混沌信号,使误差中主要是噪声与微弱信号成分。对误差采用FFT进行频谱分析,误差的能量频谱图如图5(b)所示,在 w=0.2 rad处存在明显的突起,因此能判断出信号中存在微弱周期信号。混沌同步的引入考虑了噪声、微弱信号的影响,所确定的误差比单步混沌预测模型确定的误差值更丰富,更贴近实际情况,能更好地解决检测问题。
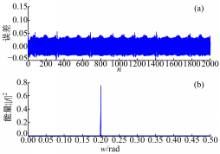 | 图6 无噪声情况下驱动信号与响应信号的误差值及噪声的能量频谱图Fig.6 Error between driving and response signalon circumstance without noise,and energy spectrum of error |
考虑更理想的情况,在混沌背景 cn中仅加入微弱周期信号,取后2000点作为驱动信号,其中 SCR=-25 dB。图6(a)是同步系统的输出信号(响应信号)与驱动信号的误差,由图可知误差呈现周期性,与图5(a)有较大差别,结合混沌背景中添加的噪声和微弱信号,说明误差与混沌背景下的其他信号密切相关,当混沌背景中存在较大噪声时,误差表现出随机特性,当存在较小噪声、较大周期信号时,误差表现出周期特性。图6(b)是误差的能量频谱图,由该图可知在 w=0.2 rad处存在突起,相比图5(b),误差的频谱在其他的频率处不存在突起,说明噪声对微弱信号的检测存在影响。
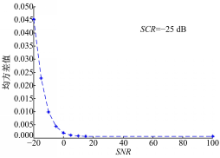 | 图7 不同信噪比下驱动信号与响应信号误差的均方差值Fig.7 Mean square error of error between driving and response signal on different signal to noise ratio |
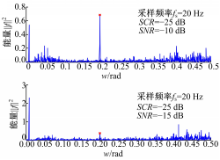
为了说明噪声强度对微弱信号检测功能的影响,在混沌背景 cn中加入 SCR=-25 dB的微弱正弦信号,但添加不同强度的噪声, SNR分别为-20、-15、-10、-5、0、5、10、15、100 dB,分别驱动同步系统,由于 SCR不变, SNR只影响噪声成分,可认为同步参数 K近似相同,计算响应信号与驱动信号误差的均方差值,如图7所示。由图7可知,噪声成分越多,均方差值越大, SNR增大说明噪声成分减少,均方差值也会减小,并最终趋向于平稳状态,当 SNR≥0 dB时,均方差值基本相同,说明在微弱信号可检测的情况下,信噪比较高时,噪声对微弱信号检测的影响小,但当 SNR<-10 dB时,均方差值变化剧烈,说明此时噪声影响明显。由上述可知,当 SNR=-5 dB时,能较好地检测微弱信号。分析 SNR分别等于-10、-15 dB时的检测效果,如图8(a)(b)所示。由图8(a)可知,当 SNR=-10 dB时,在 w=0.2 rad频率处出现了尖峰,但小于0.1 rad的频率处也出现了尖峰,该尖峰与Rossler混沌系统有关,由图1可知Rossler混沌时间序列具有伪周期性,低频率处的尖峰与伪周期性有一定联系。当 SNR=-15 dB时,虽然在 w=0.2 rad处出现了尖峰,但相比其他频率处的尖峰现象并不能说明该频率就是微弱信号的频率,不能检测微弱周期信号。结合更高的信噪比( SNR=-5 dB)和无噪声时的检测效果可知,在不同信噪比的情况下,算法的检测性能并不一样,当信噪比 SNR<-10 dB时,不能从混沌背景中实现微弱信号的检测,而当 SNR≥0 dB时,噪声对微弱信号检测的影响小。
实际环境中总是存在噪声的,分析过程中假设信噪比为 SNR=-5 dB。
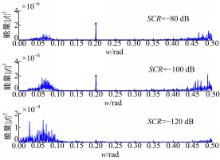
随着 SCR的不断减小,混沌背景下微弱信号和噪声成分减小,响应信号与驱动信号误差的均方差值会趋向于0,最终将感知不到信号的存在,不能实现微弱信号的检测,因此不能用均方差值说明算法的性能。选择 SCR为-120、-100、-80 dB的混合时间序列作为研究对象, SCR的变化会导致噪声与信号存在较大变化,不同 SCR的驱动信号需选择不同的同步系数 K,然后检测微弱信号,效果如图9所示。由图可知,当 SCR=-80 dB时,频谱图中在添加的频率处存在尖峰,且在其他频率处的尖峰峰值远远小于该频率处的峰值,因此能方便地检测出微弱信号。当 SCR=-100 dB时,频谱图中出现较多尖峰,该频率处仍存在尖峰,且峰值比其他频率处的峰值大,因此峰值仍可作为检测依据,但可能导致误判。当 SCR=-120 dB时,对应频率处不存在尖峰,即不能实现信号的检测。通过反复实验验证当 SCR=-110 dB时,该方法仍然能实现微弱周期信号的检测。
研究不同频率下微弱信号的检测性能,选择 SCR=-50 dB, SNR=-5 dB,频率 w为0.1,0.15,…,0.45 rad的一系列频率的微弱正弦信号分布添加到混沌背景中作为驱动信号,通过驱动信号与响应信号误差的均方差值说明该方法的性能, SCR与 SNR的值没有改变,可采用相同的同步参数 K。不同频率对应的均方差值如图10所示。从图10中可知,虽然在不同频率处的均方差值存在一定的差别,但仍属于同一数量级,可认为对不同频率的检测性能基本相似。
为了说明该方法的通用性,依托南京恒立达光电仪器厂的MKS-CEC-Ⅲ新型混沌演化控制实验仪进行实验,该实验仪能产生Coullet混沌。首先结合模拟示波器调试出Coullet相空间图[ 24],采集Coullet的 x状态作为混沌时间序列,采集某一时刻的实际数据如图11(a)所示,对数据进行滑动平均获得平滑序列如图11(b)所示。
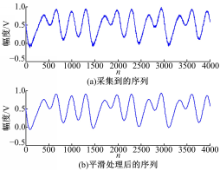 | 图11 实际采集的Coullet混沌序列和平滑处理后的序列Fig.11 Chaotic time series collected from Coullet system and the time series after smoothing |
取图11(b)中数据的前2000点作为训练数据,后2000点作为测试数据,并在测试数据中加入 SCR=-25 dB, SNR=-5 dB, w=0.1 rad的正弦信号和噪声作为测试数据 A,加入 SCR=-50 dB, SNR=-5 dB, w=0.3 rad的正弦信号和噪声作为测试数据 B,采用RBF网络实现单步预测模型的拟合,训练误差选择在1×10-7左右,然后对测试数据 A、 B分别确定同步参数 K,当 SCR=-25 dB时,同步参数 K=0 .09,当 SNR=-50 dB时, K=0 .19,说明不同信杂比情况下系统的同步参数存在差异。最后进行微弱信号的检测,两种不同信杂比情况下的检测效果如图12所示。在两种不同信杂比情况下,图中均出现了明显的尖峰,但峰值幅度存在差别,说明了微弱信号能量的差别。两种不同频率处都有较好的检测效果,说明该方法受微弱信号频率的影响小。由以上分析可知该方法能适用于不同混沌系统,能实现不同频率微弱信号的检测,具有较强的通用性。
(1)本文在混沌预测模型微弱信号检测模型的基础上,提出了基于消散型同步的混沌背景下微弱周期信号的检测方法,采用经典的Rossler混沌系统作为实验对象,分析了算法的可行性、噪声对微弱信号检测性能的影响、微弱信号频率对性能的影响等。通过实际Coullet混沌序列对方法进行了通用性分析。
(2)消散型混沌同步是混沌时间序列与混沌系统的同步,同步的引入能够分析噪声、微弱信号对混沌系统后期状态的影响,不再像单步混沌预测系统中那样忽略了两者的影响,增强了方法的实用性。该方法的预测模型不需要大量的训练,经分析该方法对所检测微弱信号的频率不敏感;在误差的频谱图中,在对应信号频率处存在较大的幅度,而非检测频率处频谱幅度小,这是基于混沌同步模型的检测方法的优点。存在一定噪声( SNR=-5 dB)的情况下,经实验验证表明该方法能检测出信杂比 SCR>-110 dB的微弱信号。通过实际Coullet混沌序列进行了方法的通用性分析,结果表明该方法能在其他混沌系统中完成微弱信号检测,具有较好的通用性。
(3)为了避免噪声和混沌杂波两者对微弱信号检测影响的重叠,定义了信杂比 SCR和信噪比 SNR,经分析可知,噪声对微弱信号检测存在一定的影响。当信杂比 SCR较高时( SCR>-50 dB),若 SNR≥0 dB,即微弱信号的能量大于等于噪声能量时,噪声对方法的检测性能影响很小,可以忽略噪声的影响,但若 SNR<-10 dB,即微弱信号的能量远远大于噪声能量时,不能检测出微弱信号,因此在实际的微弱信号检测中不能忽视噪声的影响。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|