节点定位在无线传感器网络(Wireless Sensor Network,WSN)应用中占有重要的地位,例如目标追踪、事件监测、定位路由、战场定位等^{[ 1]}。目前,针对无线传感器网络的静态节点定位算法已经趋于成熟,理论研究成果比较丰富,例如Nirupama Bulusu等^{[ 2]}提出的质心法;Lance Doherty等^{[ 3]}提出的凸规划定位算法;Andreas Savvides等^{[ 4]}提出的AHLOS算法;Radhika Nagpal等^{[ 5]}提出的Amorphous算法;Dragos Niculescu等^{[ 6]}提出的DV-Hop算法等。这些方法大多没有考虑节点的移动性,已经不能满足实际环境下的定位要求。如何设计出适合WSN移动节点的定位算法成为热点研究问题。2004年,Ling-xuan Hu等^{[ 7]}首次将应用在机器人定位领域的蒙特卡罗定位(Monte Carlo localization,MCL)算法应用到WSN中,该算法在贝叶斯位置估计的基础上,用若干带权重的采样点来描述移动节点的可能位置分布,其定位精度不仅不受节点移动的影响,反而利用其移动性来提高定位精度,减小定位代价,为WSN移动节点定位提供了新思路。国内外学者在此基础上提出了多种MCL改进算法^{[ 8, 9, 10]},但是MCL及其改进算法均是在理想环境下进行实验的,即节点的无线电射程为标准圆形区域,这与实际环境中节点的无线电射程有较大出入。

本文在MCL算法的基础上,根据不规则度的大小实时改变滤波半径的大小,为采样粒子提供随不规则度变化的权重,采样圆的圆心由原算法的估计位置改进为上一时刻的采样粒子位置,并将这一算法应用在WSN移动节点定位中,力求解决非理想环境下节点的定位问题。

MCL算法的核心思想是用 N个带权重的离散采样粒子来估计其后验概率密度,并利用重要性采样来迭代更新,算法主要包括预测阶段和滤波阶段,算法步骤如下^{[ 7, 11]}。

(1)初始化节点位置。根据未知节点的一跳和二跳锚节点,用质心法来估计未知节点的位置。

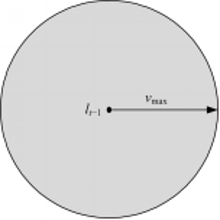
(2)预测阶段。待定节点的运动速度和方向未知,仅知道其最大运动速度 v_max,假设 l_t-1是节点前一时刻的位置,则该节点在当前时刻的位置在以 l_t-1为圆心, v_max为半径的圆内,如图1所示。

假设节点的运动速度 v在[0, v_max]上满足均匀分布, d( l_t-1, l_t)表示相邻时刻节点间的欧式距离。那么节点在 t时刻的位置估计概率为:

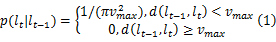
式中: p( l_t|l_t-1)称为转移方程,表示用 t-1时刻节点位置分布预测 t时刻的节点位置分布。然后在该圆内进行采样,得到节点位置分布的采样样本。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 节点预测区域图Fig.1 Predicted node region diagram

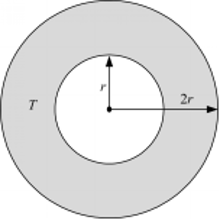
(3)滤波阶段。根据节点接收到的一跳、二跳锚节点信息对采样样本进行过滤,把不符合要求的样本过滤掉。若 S是一跳锚节点集合,如图2阴影区域所示; T是二跳锚节点集合,如图3阴影区域所示, r为锚节点的通信半径, l为采样粒子, s为锚节点, d( l, s)为点 l、 s的欧式距离,则节点 l的过滤条件可表示为:

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 一跳锚节点滤波区域图Fig.2 Filter region diagram of one-hop anchor node

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 二跳锚节点滤波区域图Fig.3 Filter region diagram of two-hop anchor node

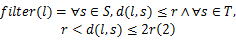
(4)重采样阶段。过滤阶段完成后,剩余的样本数目可能很少,一般不能从后验分布中直接取样,需要使用非严格的滤波条件,即将采样节点与一跳锚节点的距离进行适度扩大,比如 d( l, s) <1 .2 r,进行重采样增加样本数目,满足滤波条件的粒子称为一个采样粒子,当得到50个采样粒子时计算所有采样粒子位置坐标的均值作为节点的估计位置。

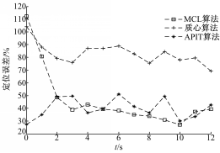
在MCL-simulator仿真环境中对常用的质心算法、APIT算法,以及MCL算法的定位误差进行仿真测试,仿真结果如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 常用定位算法性能比较图Fig.4 Performance of common localization algorithms

由图4计算各算法的平均定位误差,定位误差使用估计位置和实际位置之间的欧氏距离与通信半径的比值来表示。质心算法的平均定位误差为74.34%;APIT算法为35.99%;MCL算法为34.84%,为三者中误差最小者。同时仿真实验还表明:随着时间的推移MCL算法的精度越来越高,可以定位的未知节点越来越多,最终可实现节点的全部定位。

MCL算法的前提为理想环境,即未知节点和锚节点的无线射程均为固定值,DOI(Degree of irregular)=0,表示无线电射程在不同位置、不同发射方向、不同发射时间等条件下均为相同的值^{[ 7, 9, 11]}。但是在实际环境中,无线电射程在各个方向的值是不同的,即DOI>0,节点的无线电射程范围并非理想的圆形,其示意图如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 DOI的取值对定位精度的影响示意图Fig.5 Effect of different DOI on localization accuracy

图5中虚线表示DOI=0时的无线电射程范围,实线表示DOI=0.015时的无线电射程范围,其中通信半径为 r=100 m。

MCL算法虽然在一定程度上解决了节点移动时的定位问题,但是当节点的无线电射程非理想时,或者节点的速度较快时,不能取得较好的定位精度,基于此,分别从预测阶段和滤波阶段对MCL算法进行改进。

2.1 预测阶段

MCL算法采用重要性采样,即从粒子密度高的区域进行采样,基本思想是选择一个建议密度 q( x)来代替难以采样的真实概率密度 p( x),则MCL积分问题可转变为:

式中: p( x)为实际密度; q( x)为代替 p( x)的估计密度。假设 q( x)的形状覆盖了 p( x)的形状,即 q( x)的定义域要大于等于 p( x)的定义域。

MCL算法中的重要性采样利用多个 q( x)独立样本的加权来近似:

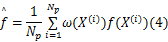
式中: N_p为采样粒子个数; ω( X^{( i)}) =p( X^{( i)}) /q( X^{( i)})为权重,由于 p( x)归一化是未知的,应满足 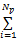ω(X⁽ⁱ⁾)=1,于是得到:

式中: ( X^{( i)})为归一化权重,其方差

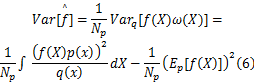
要想提高定位精度,则需降低方差值。由式(6)可以看出, q( x)与 p( x)形状越相似,方差越小,精度越高。 MCL算法是以上一时刻节点的估计位置为圆心进行采样的,本算法采用以上一时刻的采样点为圆心进行采样,这样可使得 q( x)与 p( x)形状更相似,从而提高定位精度。

2 .2 滤波阶段

2 .2 .1 自适应滤波条件

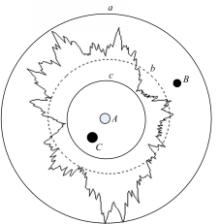
由于实际环境中 DOI>0,如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 DOI>0时的采样点区域分布图Fig.6 Distribution diagram of sampling points when DOI>0

点 A是一跳锚节点,点 B、点 C为经过预测阶段的采样点,虚线圆 b是理想的无线电射程,不规则实线是实际的锚节点无线电射程。改进算法根据 DOI的大小对通信半径的影响修改其滤波条件,表示为式(7),对于一跳锚节点的采样粒子,该采样粒子与锚节点的距离 d( l, s)小于锚节点半径 r与 r*DOI的和,如图6中的圆 a所示,圆 c为实际锚节点无线射程的内切圆,表示必定在一跳锚节点 A射程范围内点的集合。

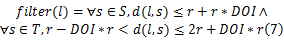
2 .2 .2 自适应权重

由自适应滤波条件可知,改进的 MCL算法考虑到不同区域的锚节点会影响定位误差的大小,当采样节点处在锚节点无线射程不同的采样区域时,对未知节点的影响是不同的。图6中 C点肯定在锚节点的无线射程范围内,权重设为1;而 B点由于不规则度的影响,不一定在锚节点射程范围内,其对未知节点和待定位节点的影响与 C点不同。基于此,本算法对于采样粒子样本权重进行调整,考虑到滤波条件的改变,若所有粒子的权重均相同则不符合实际情况,由此对满足不同滤波条件的采样粒子赋予相应的权重。当采样点绝对满足节点的无线射程时,即在圆 c中时,权重设为1,当满足放松限制后的条件,即在圆 a和圆 c之间时,节点的权重随着 DOI的改变而改变,由于圆 a与圆 c间的面积与节点的 DOI成正相关关系,为了简化,本算法将圆 a和圆 c间的采样点权重定义为DOI *r/r,则节点综合权重条件设置为:

本算法考虑到了不规则度的影响,处于不同区域的采样粒子对节点定位的影响不同,因此对滤波阶段进行的自适应滤波和自适应权重的改进恰好弥补了原算法的缺陷,提高了定位精度。

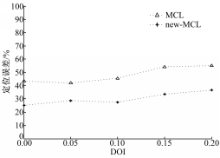
在 MCL-simulator仿真器下,设置 WSN区域大小为500 m×500 m,节点总数为320个,其中锚节点32个,锚节点和未知节点的通信半径均为50 m,锚节点的速度 v_s∈[ S_min, S_max], S_min和 S_max分别表示锚节点的最小速度和最大速度;节点的速度 v∈[ v_min, v_max], v_min和 v_max分别表示节点的最小速度和最大速度。对每种算法进行10次实验,每轮中节点进行80步的移动,最后求得80次定位误差的均值。节点具有判断某个节点是否在通信范围内的能力,但是没有测距能力;有感知自己速度大小的能力,但是没有感知运动方向的能力,定位误差使用估计位置和实际位置之间的欧氏距离与通信半径的比值来表示。图7是 MCL定位算法和自适应 MCL定位算法( new-MCL)在不同的 DOI下的定位误差图,其中锚节点和未知节点的最大速度为50 m/s。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 不同DOI下节点定位误差对比图Fig.7 Localization error of nodes comparison under different DOIs

由图7可知,随着 DOI的增大,节点的无线电传播模型越来越不规则,但 new-MCL的定位精度总是好于 MCL,平均定位误差下降了约13 %。随着 DOI的逐渐增大, MCL和 new-MCL算法的定位误差均有一定程度的增大, new-MCL的定位精度在不规则度为0 .1时定位误差达到最小。

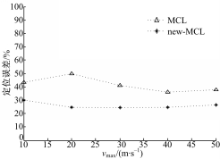
图8是随着 v_max的增大 new-MCL与 MCL的平均定位误差曲线比较图。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 vmax对定位误差的影响Fig.8 Effect of vmax on localization error

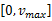
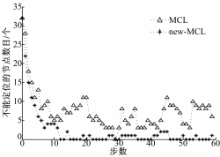
假设未知节点和锚节点的最大速度相同,均为 v_max,两者的实际运动速度均匀分布在 ,从图8可以看出,随着 v_max的逐渐增大, new-MCL定位误差始终低于 MCL,平均定位误差下降了约10 %。

图9是节点运动60步,每一步定位时无法定位节点的数目。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 无法定位的节点数目对比图Fig.9 Number comparison of nodes can not be located

由图9可以看出,改进后的算法无法定位节点的数目低于 MCL算法。46次以后,改进后可定位的数目约为100 %。对60次不能定位节点进行平均得到 MCL不能定位的数目约为7 .6717个,改进的算法不能定位节点个数为2 .3333个。 MCL算法网络的覆盖率为97 .36 %, new-MCL算法的网络覆盖率为99 .19 %。这是由于滤波条件的放宽,使相同的采样次数下满足条件的采样粒子数目增加,从而增加了可定位节点的数目。

大多数 WSN节点定位算法是针对静态网络提出的, MCL利用节点的移动性来协助定位。本算法在 MCL算法的基础上,针对其在非理想环境中定位精度不高,网络覆盖率较差等缺点,在节点预测和滤波阶段分别进行了改进。在预测阶段以上一时刻的采样点为圆心进行采样,滤波阶段根据 DOI的不同自适应调整不同区域采样粒子的权重,从而在非理想环境下提高了 WSN节点的定位精度和网络覆盖率。