标识点的自动识别、快速提取和高精度定位是计算机视觉、目标识别、相机标定、相对定向中的一个重要而基础的问题,自动识别的速度、稳健性,尤其是标识点的定位精度仍然是限制自动识别在一些场合应用的瓶颈问题。

匹配领域的特征点提取算法,例如Harris、DOG、SUSAN等算子^{[ 1]},通常只能达到亚像素级的精度,并且存在很多伪特征和漏特征现象。数字相关法具有原理简单、适应性强和精度高等优点,但在旋转目标中很少用到,因此时模板选择难以实现^{[ 2]}。

圆心(椭圆圆心)拟合、形心法和灰度重心法是针对中心对称目标的亚像素算法,重心的特征拟合具有速度快的特点,但是对各向异性的灰度,例如光照、特征的不规则性非常敏感^{[ 3]},其定位精度可达0.2~0.5个像素^{[ 2]}。小面元拟合具有一定的通用性^{[ 4]},但其定位精度通常只能达到0.3个像素左右。二项式的极点或鞍点可用来定位,当邻域的半径足够小时,可以一定程度地抵消透视变换和非线性变形,而拟合法的前提是目标的特性满足已知或假定的函数形式^{[ 5]},所以一般很难获得很高的亚像素精度^{[ 2]}。文献[6]介绍了Zernike矩、Hu不变矩、Wavelet矩,并利用它们定位特征点,然而统计窗口与形状的确定是个潜在的问题,计算量也很大。圆和有尺寸的角点也存在一个共性:中心会受到透视变换的偏移;一些边界的提取会在一定程度上增加计算负担;模型中较多的参数通常带来解算结果的不稳定性,陷入局部极值的可能性非常大。

数学模型拟合直线或曲线求交点的方法(例如用基于Hough变换的思想估计直线,并不断排除偏离较大的点,然后拟合直线的参数^{[ 7, 8]},并求取交点),虽然Hough变换及其改进方法的稳健性较好,但不可能达到很高的精度。文献[3]等利用棋盘网格的交点为一点、不易受透视变换和非线性畸变影响的特点,能提取0.1个像素级精度的交点。然而在实际过程中,棋盘格的颜色过渡为渐变的,没有较明显的边界信息,这对下一步的精确定位提出了挑战。

针对上述问题,本文设计了一种快速的标识点提取算法,并在标识点提取的初始位置上进行单点式中心对称匹配与求中心的迭代。整个过程包括高分辨率影像的局部降噪和除去背景的方法、标识点的快速提取算法、单点式迭代匹配修正等环节。并针对多种环境下的标识点,在不同的噪声、光照等环境下进行了大量试验,对试验结果进行了剖析和总结。

为了有效去除噪声和背景对标识点提取的影响,高精度地提取标识点的精确位置,需要对图像进行必要的反色和预处理。

首先,如果图像是白色网格黑色线条,将“+”线条按颜色分量合成并反色(如果是黑色网格白色线条,则只需进行颜色分量的合成),即:

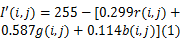
然后对图像进行高斯平滑,去掉高频噪声分量:

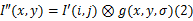
式(1)(2)中: g( x, y, σ)为方差为 σ²的高斯函数;􀱋表示卷积; r( i, j)、 g( i, j)和 b( i, j)分别为原始影像的三原色分量。 I'( i, j)和 I″( x, y)分别为变化后的灰度图。

为了消除不同光源或显示器不同角度成像时局部和整体数据统计规律不一致的特点,将高分辨率的网格影像划分为有一定重叠的动态网格。统计分块簇图像的灰度直方图 G_table( i),为更加稳定地探测峰值和谷值,对图像的直方图进行高斯平滑:

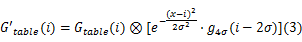
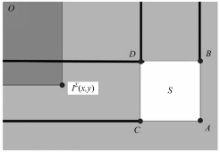
式中: g_{4 σ}()表示宽度为4 σ的门函数; σ²为高斯方差,然后采用非最大值抑制,探测出峰值点和谷值点。由于噪声、光照、视角等因素的影响,可能存在多个峰值点和谷值点,利用能量最大的“波峰”,并配合“波谷”以及一定权重的非极大峰值和谷值检测出分界岭,然后将小于分界岭的数值赋为0,保留灰度值大于分界岭的值,从而实现局部图像的背景分离,如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 高分辨率网格标识点影像的预处理前后效果对比Fig.1 Effect of pre-disposing for high resolution images of cross points in mesh

特征的检测和获取过程中需要多次解算邻域的灰度质心、灰度统计量和一阶统计量,图像的迭代积分^{[ 9]}可以加快处理的速度。

若图像的积分记为 I^Σ( x, y),则:

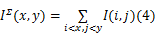
可利用迭代算法快速解算上式:

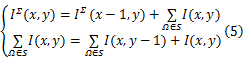
其中,迭代初值为0,当坐标值小于0时,相应项的响应值为0。于是,特定区域 Ω内( Ω∈{( x, y) |i-r₀ <x<i+r₀, j-r₀ <j<j+r₀})的统计量 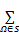I( i, j),其快速获取方法如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 图像的积分和局部统计量的快速获取示意图Fig.2 Accumulative of image and quick calculating method

即有:

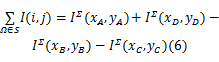
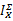
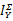
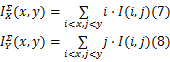
同理,定义 ( x, y)和 ( x, y)为影像分别在 X和 Y方向上的统计量:

类似地,可计算:

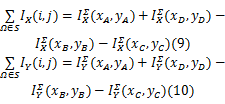
检测交点时,采用如下的约束条件:

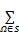
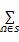
(1)只有当 I( i, j)大于一定阈值时,才考虑其作为提取中心点的候选点或区域,因为在空白区域时, I( i, j)的值接近0。此约束将搜索范围控制到“+”线条上。需要注意的是,此时能量的极大值点理论上处在参考点附近的“+”两条相交直线的中心线上,而并非中心点。

(2)计算参考点上下左右邻域(距离在线宽之外的邻域)的灰度累积量,只有当左右和上下之间的变化量的比例均较小时,即该点的对称性较好时才进一步考虑。此约束将点的搜索范围控制在参考邻域“+”两条直线的中心附近。

(3)分别计算上下左右邻域影像块的灰度质心,即:

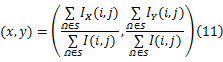
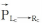
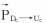
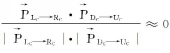
由于对称型标识点的邻域具有对称性,所以其左重心与右重心形成的矢量 ,以及上重心和下重心形成的矢量 ,满足近似正交。即:

据此,可将对称性不好的点排查在阈值范围之外,例如阈值取arccos(85 ×π/180)表示不垂直的程度小于5°。

(4)将线段 L_CR_C与 D_CU_C的交点确定为角点的初始位置。

(5)此时在某一微小邻域仍然存在多个可能的交点,选择交点最接近两条线段中点的点作为最优候选点。

至此可以比较准确地快速确定“+”交点的准确位置,由于“+”标识的对称性,图像旋转不影响算法的性能。本算法将传统的提取标识点的程序的复杂度从 O( N⁴)以上降到 O( N²),大幅度减少了处理时间,并且每个点邻域实现最优意义上的初始位,保证了“+”交叉点的重现率。

在相机标定^{[ 10]}时,固定网格的实际宽度,在图像中设置大小不一样的几个圆形或矩形点作为基准点,便可通过候选点能量大小的排序自动识别。然后,以基准点为基础,利于网格点的空间分布规律进行扩散,便可实现其他点空间坐标的自动赋值,从而快速实现标识点的像素坐标与空间指示坐标的全部自动对应。

由于“+”字型的标识点具有左右对称、上下对称以及中心对称的特点,可将高精度的影像相关的思想用到自身和自身变换图像的匹配上。

如图3所示,对于某初始标识点的位置点 P₀见图3(a),经过180°旋转后,其位置变为图3(b)中的点 P₁,然后利用高精度的仅平移约束下的加权最小二乘影像匹配方法(详见本节最后部分描述)以图3(a)中的 P₀为模板,将图3(b)中的点 P₁与 P₀进行匹配,可得到匹配点 P₂的位置如图3(c)所示,然后将图3(c)旋转180°后得到如图3(d)所示的点 P₄,此时点 P₄与 P₀所处的坐标系一致,然后取点 P₄与 P₀的中点 P₅即为 P₀调整过后的“+”中心点,如图3(e)所示。多次(一般3次即可)迭代后便可得到精度更高的点的位置。

图3

Fig.3

	Figure Option ViewDownloadNew Window
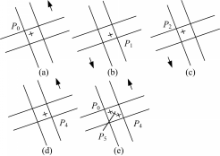	图3 对称型标识点高精度单点匹配式定位示意图Fig.3 Accurate locating by single-point-mode matching for symmetric marking points

对于图像的翻转操作(旋转180°),仅需要将像素重置即可,不需要图像的重采样,因而避免了人工引入的采样和量化噪声。

由于此时的图像仅存在翻转变换,变换后标识的几何分布不变,尺度信息及比例关系不变,局部的光照条件亦不变,所以仅需考虑图像的平移变化,故:

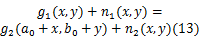
式中: n₁( x, y)和 n₂( x, y)表示局部影像的噪声,尤其是不对称性噪声分量; g₁( x, y)和 g₂( x, y)分别表示原始标识图和翻转后对应标识图的灰度值,用全微分一次项表示上式有:

利用最小二乘残差的原理^{[ 11, 12]}构造误差函数有:

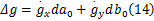
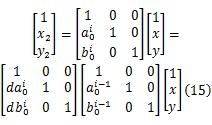
距离参考点 x_i较近的点取较大的权值,权值函数采用Sinc函数,记权值矩阵为 W, W=^∧( w₁, w₂,…),于是

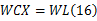
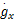
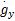
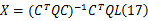
式中: C表示微调量 ( i, j)和 ( i, j)组成的系数矩阵; L表示 Δg列向量,通过加权最小二乘求得:

如果 C^T QC不可逆,则采样广义逆矩阵求解。并在初值( a₀ =0, b₀ =0)下,通过如下迭代过程微调点的位置:

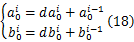
直到迭代参数调整量很小,或者残差函数值变化很小,或者开始发散为止。

测试图片的生成与基准点位置的确定:假设线宽为 W_L,方格的宽度为 W_B。对应的第 M行第 N列的网格交点即“+”中心点 P( M, N)的坐标为:

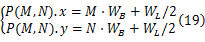
然后对上式进行旋转、加入噪声、反色后等变换。噪声为随机分布的高斯白噪声,设其规格化后的值域为[ -1,1],转化为噪声所占的比例为 N_G,即对应于[ -N_G, N_G]。为保证图像变换的精度,插值采用三次近似Sinc曲面插值。

对于旋转变化,对应网格点的真值为:

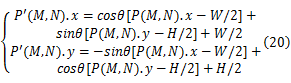
式中: W和 H分别表示影像的宽和高。

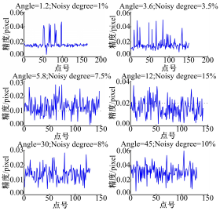
试验中, W_L为3个像素,W _B为50 个像素。图4为一组变换参数在不同噪声下对定位精度的影响。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 本算法在不同噪声比例和图像变换下的定位精度Fig.4 Accuracy of proposed algorithm under different situations

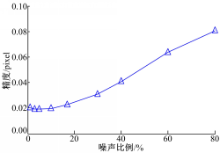
固定角度和尺度变化量,测试噪声对本算法的影响,如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同噪声比例对本算法定位精度的影响Fig.5 Effect of noisy on accuracy of proposed algorithm

图像旋转变化产生较大直线走样(此时用双线性插值)下的定位误差如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
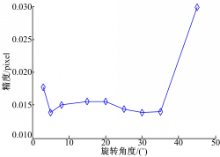	图6 细线条图像旋转产生较大走样对本文算法定位精度的影响Fig.6 Effect of rotating resampling error of digital image with thin lines on accuracy of proposed method

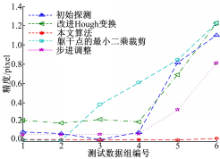
在与图4相同的环境设置下,本文算法与改进Hough变换直线求交算法(简称改进Hough变换法)、最小二乘直线拟合与裁剪然后求交点算法(简称躯干点的最小二乘裁剪法)、对称性约束惩罚函数盲采样步进调整算法(简称步进调整法)进行比较,结果如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 本文算法与一些经典算法的定位精度比较Fig.7 Comparison of accuracy among different algorithms

时间开销比较如表1所示(共试验6次,取其平均值),试验环境为VS2005下的VC++,PC机内存为4 GB,主频为2.93 GHz。

表1

Table 1

表1(Table 1)

表1 本文算法与一些经典算法时间开销对比表 Table 1 Comparison of time cost among different algorithms 算法 时间开销/s 1 2 3 4 5 6 平均 初始探测算法 5 5 4 7 4 6 5.17 改进Hough变换法 10 13 12 11 9 10 10.83 本文算法 10 8 13 8 16 16 11.83 躯干点的最小二乘 裁剪法 7 8 4 7 9 8 7.17 盲采样步进调整法 60 53 68 52 58 63 59

表1 本文算法与一些经典算法时间开销对比表 Table 1 Comparison of time cost among different algorithms

试验表明,噪声会一定程度降低定位精度,量化误差会较小程度影响本文算法的定位精度。就抗噪性能而言,改进Hough变换法稳健性相对较好,躯干点的最小二乘裁剪法容易受到一些异常解的影响,步进调整法抗噪性能较好,但在时间开销上很大,通常在 O( N⁶)以上,本文算法最好。针对采样和量化误差的影响而言,改进Hough变换法、躯干点的最小二乘裁剪法和步进调整法均不能适应图像本有的非对称量化噪声(数字影像将距离采样信息反映为等像素宽度的像素亮度差异),并随着这种变化呈现比较一致的偏离,本文算法能够适应这种变化,一定程度修正这种几何不对称变化;从时间开销上讲,本文算法与改进Hough变换法和躯干点的最小二乘裁剪法相当,而远小于步进调整法;从定位精度来讲,步进调整法比其他两类方法高,但远低于本文算法。

采用多种对称型标识点和多种环境下的标识点进行试验,本文算法均能取得理想的效果,稳健性强,识别准确,定位精度高。依据文献[10]的评定指标,本文算法的重复定位误差小于10^-5像素,稳健性和定位精度远大于文献[10]中10^-2像素量级的水平。

在图像的局部高斯平滑去噪和二值化思想去背景的基础上,利用图像整体的累积量和一阶矩统计量,通过标识点邻域的对称性、高亮度性等特点,设计出了基于灰度中心和几何重心“+”交叉点等约束的快速稳健标识点探测与初定位;然后利用单点式匹配算法微调交点的精度,大大提高了标识点的定位精度。本算法能够有效适应图像的旋转、尺度变化、光照变化以及一定量的不对称噪声、透视变形等影响,达到0.01~0.05像素级的定位精度。通过密集布设的网格的自动识别和定位,可大幅度提高相机标定的自动化水平和精度;通过地面标识点的自动提取和高精度识别,可以在极少数人工标识点的情形下全自动相对定向以及空间解算;此方法也可为一些精度较高的航天器空间对接与制导提供技术支持。