作者简介:田文飚(1987-),男,博士研究生.研究方向:压缩感知.E-mail:twbi5si@gmail.com
为提高现有直接信息均匀压缩采样(Analog to information conversion,AIC)的观测效率和性能,在能量准则下,提出非均匀信息采集(Non-uniform information acquisition,NUIA),充分利用信息的重要性先验,即对信号随机调制后,依据能量进行变速率的采集,能量越大的信号段采样速率越高,反之亦然。结合支撑域扩充、剪枝的思路提出变速匹配追踪(Variable rate matching pursuit,VRMP)算法,通过引入非均匀观测的先验支撑集,并在追踪过程中将其与迭代估计出的支撑集相并,提高了重构精度。理论分析和实验结果表明了NUIA-VRMP的有效性。特别地,相比于常规AIC的子空间追踪重构,NUIA-VRMP的组合能在低采样速率条件(如20%的Nyquist速率)下获得50 dB的重构增益。
The existing Analog to Information Conversation (AIC) is based on uniform-low-rate information measurement, and the importance prior information contained in the signal is underused. Under the energy criterion, a Non-Uniform Information Acquisition (NUIA) method is proposed. After random modulation, the signal is sampled at non-uniform-rate that the bigger the energy is the higher the sampling rate is and vice versa. Combing the idea of support merger with pruning, a Variable Rate Matching Pursuit (VRMP) algorithm is proposed. The prior support set, which is united with the set of signal appropriation support, is able to promote the recovery accuracy. Compared with the Subspace Pursuit (SP) reconstruction of conventional AIC, the combination of NUIA-VRMP can obtain 50dB reconstruction gain at ultra-low-rate, (e. g. 20% Nyquist Rate).
绝大多数压缩感知[ 1, 2, 3](Compressed sensing,CS)理论关注的都是那些能够在离散、有限维字典上稀疏表示的信号。然而,在遥感、通信和雷达等应用领域中所呈现的信号往往是一些连续信号。模拟信号直接信息压缩采样[ 4, 5](Analog to information conversion,AIC,以下简称直接信息采样)巧妙地以硬件形式实现了感知矩阵的生成及其与模拟信号的乘法,即跨越了信号压缩感知过程中模拟-数字间的鸿沟。AIC着眼于可压缩的模拟信号,通过对其进行随机调制、低通滤波及低速采样后得到数字化的压缩观测值,实现数字化与压缩同步进行,在接收端采用求解优化问题的方式重构出原始信号。技术层面上,AIC主要采用随机PN序列调制信号并进行低通滤波后再输入常规ADC器件的手段,均匀、低速地获取信号的观测。Laska等[ 6]给出了其中相关电路的设计方案。近年来,AIC又衍生出了几种变型,包括利用积分器替换低通滤波器的信息采样框架[ 7]以及基于分段压缩感知(Segmented compressed sampling)的AIC[ 8],用基于多路并行混合器和积分器组的结构实现。
现有AIC框架内的信息采集都是基于均匀采样的,这样的采集方式实际上没有充分考虑信号中蕴涵的不同信息在信号重构中的不同地位,观测效率和性能均有待提高。现实生活中人们关注的信号,如:语音、图像、核磁共振成像等大都是稀疏的或“可压缩的”信号[ 2],若以能量为准则衡量信号中蕴含信息的重要性,且假设信号在小波域上稀疏,那么,信号的尺度系数占据绝大多数能量,即其在信号重构中更加重要。
本文提出对信号随机调制后,依据能量进行变速率地采集,能量越大的信号段采样速率越高,反之亦然,即所谓的非均匀信息采集(Non-uniform information acquision,NUIA)。由于感知矩阵的不均匀性会使得现有的典型算法,如正交匹配追踪(OMP)[ 9]、子空间追踪(SP)[ 10]、基追踪(BP)[ 11]等对此类问题的求解性能较差。因此,结合支撑域扩充、剪枝的思路提出了变速匹配追踪(Variable rate matching pursuit,VRMP)算法,通过引入非均匀观测的先验支撑集,并在追踪过程中将其与迭代估计出的支撑集相并,提高重构精度,算法能在低采样速率条件(如20%的Nyquist速率)下重构原信号,NUIA-VRMP的采集、重构组合能够获得比现有方法更高的重构增益。
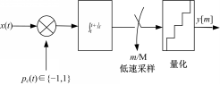
通过AIC,信号的采样和压缩可以真正同时低速进行,使采样和计算成本大大降低。该理论指出了将模拟信号直接采样压缩为数字形式的有效途径,具有直接信息采样特性。其设计框架[ 7]如图1所示。
直接信息采样系统由三部分组成:调制器、积分器以及常规采样单元。模拟信号首先被一个 N Hz(2倍的信号Nyquist频率)的伪随机最大长度PN序列 pc 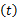
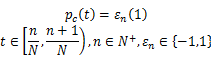
接着对调制后的信号进行低通滤波,这里的低通滤波简化为一个积分过程,完成1/ M(s)时间内调制信号的累加。调制的目的在于扩展频谱以保证低通滤波后信息的完整性。最后利用常规的ADC器件以速率 M进行采样、量化后得到信息观测值序列 y[ m]。AIC以固定速率 M进行采样,这种采样方式没有充分利用信号本身蕴含的先验信息,使其采集效率和重构性能都有待提高,由此引出本文的主要研究内容。
在能量准则下,即以能量来衡量信号中蕴含信息的重要性,非均匀信息采集(NUIA)依据输入信号的幅度值控制采集速率,幅度值越接近前级限幅器的最大幅值,则采样速率越接近预设最大采样速率(如信号的Nyquist速率);反之,幅度值越接近0,则采样速率越接近预设最小采样速率(如10%的信号Nyquist速率)。其设计框架如图2所示。
不妨在1 s内考察整个系统(当然也可以选择其他时长),现以离散时间表示信号,令:
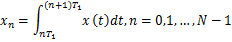
式中: T1 =1 /N为PN序列一个码元的持续时间,在这个时间间隔内PN序列取值为一个常数。先来考察积分器对信号的作用。这里,仍然假设模拟信号中所蕴含信息的速率是有限的,即信号在某个变换域上稀疏[ 2],换句话说,信号应当能由有限的连续基或基字典元素线性组合表示。这里不妨先设信号在频率域稀疏,即:
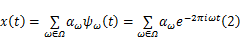
式中: Ω为一个只包含 K个频率值的集合,满足:

式中: N为信号Nyquist频率的2倍。可将 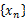
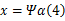
式中: α为信号中所包含的信息,其中:
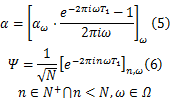
因为PN序列一个码元的持续时间为 T1 =1 /N,在1 s内PN序列的 N个码元构成码片序列(Chipping sequence) ε0, ε1,…, εN-1,对信号的作用可写成矩阵形式 xaDx,其中:
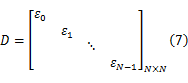
接下来考察变速采样器的影响。信号观测值可表示为:
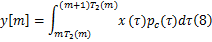
式中: T2 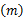
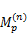

式中:max 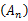
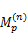

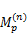
低速采样器的作用可表示为一个 M×N的矩阵 H,每一行对应一个观测值,且每行元素值的平方和恰好为 N/ 
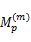
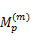

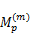
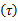

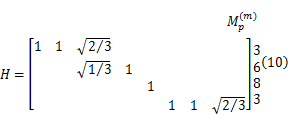
式中: H是一个非均匀采样矩阵( M=4, N=8)。文献[7]给出的均匀采样矩阵实际上可以视作是上述矩阵的一种特例。图3为一组均匀、非均匀采样矩阵稀疏结构的对照,非零元素以点的形式描绘出来。由采样矩阵的物理意义可知,图3(b)中斜率大的部分相比斜率小的部分对应的采样速率更大。
构造感知矩阵 Φ=HDΨ,信号观测值可表示为矩阵形式:
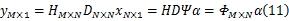
每次迭代时,贪婪追踪算法从信号中选取与感知矩阵最相关的一个或一组原子作为支撑集,然后,重建信号并计算与原信号的残差,通过残差选取新的原子来更新支撑集,从而重构信号。以 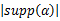
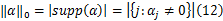
若 α为稀疏信号, Λ=supp 
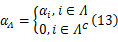
式中:矩阵 H由信号瞬时采样速率 Mp决定,其中携带了信号的先验信息,由式(9)可知,在能量准则下,信号越重要,瞬时采样速率越大,反之亦然。考虑用 Mp来估计 x在变换域上的支撑集:
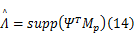
在VRMP重构算法中,选取 ΨT Mp中最大的 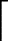

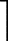
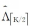



输入:观测值向量 yM×1 ,感知矩阵 ΦM×N,信号瞬时采样速率 Mp。
输出:重构信号 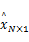
Step1初始化:初始残差 r1= y,求信号的先验支撑估计,重构信息 

Step2更新投影系数 vn= Φrn,获取其前若干个大元素对应的指标集 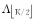
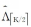
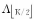
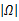

Step3通过最小二乘法计算信号估计: b 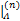
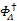
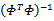
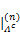
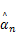
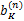
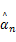
Step4更新残差 rn= y-Φ 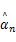
Step5若 
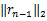

信号的重构可视为一个欠定稀疏方程组 y=HDx的求解问题,正是由于 H的不均匀特性使得现有的典型求解算法如OMP、SP、BP等对此类问题的求解性能较差。 H对信号的作用类似于一种能量的均衡,因为信号能量大时采样速率也大,众多采样点分摊了信号能量,信号能量小时采样速率低,积分器累加了这些能量。于是信号观测点之间能量差异被缩小,进而使得重构时投影系数(即 vn= Φrn)差异缩小。而类似于OMP、SP的贪婪算法正是基于搜索最大投影系数进行重构的,因此将其应用于非均匀采样重构性能不理想。
从算法流程来看,VRMP算法实际上是对SP算法的改进推广和应用。每次迭代之初,两种算法均是扩充总数为 K的原子,不同的是,SP扩充的是 K个最大相关系数的索引,VRMP扩充的 K个原子中包括了 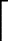
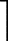

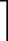

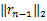
定理1 (有效性)若信号 x在变换域 Ψ上稀疏度为 K,其观测值满足式(11),若感知矩阵 Φ满足参数为 
公理1 若信号 x和感知矩阵 Φ满足上述RIP性质,非均匀采样的瞬时采样速率 Mp由式(9)确定,可重写作:

式中: C和 Mmin为常数,则VRMP算法能够等价于一个引入先验支撑 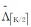
根据式(9)(15)描述的顺时采样速率 Mp与信号幅度 An的关系,可利用式(14)估计信号的支撑集。然而,目前仅能以公理形式给出且利用实验验证 
定理2 (可靠性)假设条件与定理1相同,并假定观测信号被噪声污染, y=Φα+e,噪声 e能量为 σ2。若感知矩阵 Φ满足 δ3 K<0.083的RIP特性,那么VRMP算法重构信号误差满足:
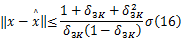
该定理也依赖于公理1所述VRMP与SP的关系,证明详见文献[10]定理9。
另外,前期研究已经给出了依据感知矩阵RIP参数判断信号稀疏度的分治试探方法[ 14],逆向运用此判据则可利用稀疏度已知的信号来试探出感知矩阵的RIP参数 δK。
取长度为 N=1024点的一维稀疏测试信号(本实验中使用的是MATLAB环境下的Leleccum信号),稀疏度 K=80。实验过程中,固定最低采样速率 Mmin为10%的Nyquist速率(即0.1 N),最大采样率 Mmax在0.1 N~1.5 N范围内浮动,使得观测的平均压缩比 M/N∈ 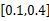
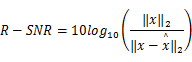
杨海蓉等[ 15]综述了若干种压缩感知重构算法,其中常规均匀采样条件下,SP比其他同类算法(如OMP、ROMP等)重构性能要好。另外,盲稀疏度自适应匹配追踪(BSAMP)算法[ 14]与本文类似,同样是通过引入信号先验达到增强重构性能的目的,不同之处在于其思路是利用分治试探预估计信号的稀疏度并精确重构出原信号。因此,这里选用SP作为常规AIC的重构算法与非均匀采集下的重构作对照,考察非均匀采集及重构性能。在非均匀采集框架下,重构算法选择典型的SP、OMP、BP(用CVX工具箱[ 16]实现)和BSAMP与本文提出的VRMP对照。
若认为R-SNR>20 dB时,信号被成功重构,2000次模拟实验中重构概率随平均压缩比收敛曲线如图4所示。
非均匀采集下变速匹配追踪(对应NUIA-VRMP)的重构概率随平均压缩比升高而增大;相同压缩比下,NUIA-VRMP重构概率大于常规AIC下性能最好的SP重构,也大于非均匀采集下的其他算法的重构概率。若在重构时都采用SP算法,那么非均匀采集下的重构概率会低于常规均匀采集下的重构概率,这是因为,SP算法没有充分利用信号的重要性先验,而非均匀采样对信号类似能量均衡的作用使得恢复矩阵的列向量和残差的投影系数(内积值)差异缩小。因此,基于搜索最大投影系数的贪婪算法(如OMP,SP等)应用于非均匀采样重构性能不理想。解决这个问题正是提出VRMP算法的初衷之一。由于BSAMP的稀疏度估计是基于均匀采样提出的,因此,在非均匀采样条件下,重构结果因其稀疏度估计不准确而不是很理想。NUIA-VRMP的组合在低采集速率下(平均压缩比为20%时)重构概率为95%。
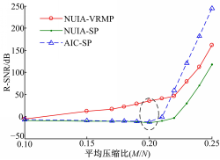
图5给出了2000次Monte Carlo实验中的平均重构信噪比随平均压缩比变化的规律,可以看出,非均匀采集下的变速匹配追踪(NUIA-VRMP)在低采样速率下,R-SNR大于常规AIC下性能最好的SP算法的对应值。特别地,相对于AIC-SP的组合,在平均压缩比为20%时,NUIA-VRMP的组合能获得50 dB的重构增益。
针对常规AIC采集效率及重构性能有待提高的问题,本文提出了非均匀信息采集(NUIA),同时,提出变速匹配追踪(VRMP),考虑依据信号重要性先验信息判断出感知矩阵中与重要的信号段最相关的若干列,利用这些先验支撑组成的子阵对信息进行首次试探性重构,提取感知矩阵中与残差最相关的若干列,并与先验支撑求并集以扩充重构子阵。每次迭代时,只保留重构信息前若干项系数以剔除冗余。由此循环迭代保证重要信息的重构质量。相对于AIC-SP的组合,NUIA-VRMP的组合在低速率下(如平均压缩比为20%时)能获得50 dB的重构增益,且重构概率为95%。本文中讨论时认为R-SNR>20 dB信号被成功重构。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|