城区树冠是城市生态系统的一个重要组成部分,它是评价城市生态的一个重要生物物理指标。城市绿量(Living vegetation volume,LVV)是指绿化植物茎叶所占空间的体积,它是城市绿化指标体系的第一个立体指标^{[ 1]},LVV在研究绿化布局、数量及其与大气环境的相关关系方面具有重要意义^{[ 1]}。

从城区树冠信息提取的数据源来看大部分集中于航空遥感影像、多光谱卫星遥感影像、高分辨率卫星遥感影像。从城区树冠信息提取的方法来看大部分集中于常规的监督分类和非监督分类^{[ 2]}。文献[3-5]研究以高分辨率遥感影像提取树冠信息,其基本方法包括学习与监督、基于区域增长、分水岭或模板匹配等以及这些方法的混合,少有考虑影像尺度问题对树冠识别的影响,特别是在高分辨率影像中,树冠纹理结构高度细节化,造成在固定尺度下,上述方法都很难获得理想结果。

针对多尺度目标识别问题,文献[6]提出用小波分解的高、低频系数的标准偏差与均值构成纹理影像的多尺度金字塔特征空间,用于纹理影像的多尺度分割,但是,该方法在进行多尺度特征传递过程中,造成了不同尺度特征空间的复杂性,加大了均值漂移(Mean shift,MS)带宽等参数选择的困难。因此,本文提出利用小波分解建立多尺度特征空间的金字塔结构,通过城区树冠内、外部结构差异以及平均光谱辐射强度差异计算目标特征,采用改进后的约束均值漂移(Constrained mean shift,CMS)方法,解决多尺度聚类导致的特征空间复杂化问题,最终解决了由于基本特征因素(例如光谱、纹理或尺度)缺失造成的树冠识别缺陷。采用小波金字塔结构,由于下采样导致小波分解的第一层特征影像尺度是原始影像的1/4,降低了影像分辨率,因此本文进一步提出基于聚类特征的监督分割方法,细化分割结果。本文方法在高分辨影像上取得了很好效果。

小波变换为纹理分析提供了一种多尺度的集频谱、影像结构和像素统计基础于一体的综合分析方法^{[ 6]},具有良好的空间和频率分解特性,它通过伸缩和平移等运算功能对影像进行多尺度分解,是性能极好的影像多尺度多通道分析工具,为纹理影像在不同尺度上提取和表示特征提供了精确统一的框架。本文采用对低通信号(近似影像)进行递归分解,每一层均由低通和高通信号构成特征空间,从低层到高层纹理特征逐层分离,构成小波系数特征空间的金字塔结构。

根据特征计算原理,函数 f( x)的连续小波变换为:

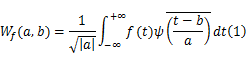
式中:函数 ψ( x)∈ L²( R)是基小波; a为伸缩因子; b为平移因子。

对连续小波变换的尺度因子进行二进制离散化,同时也对平移因子进行离散化,即 a=2 ^j, b=2 ^jk,( j, k∈ Z),这样就得到对尺度与时间都离散化的小波变换。

在纹理分割中,基小波的选取主要考虑其正交性,使所提取的纹理特征之间尽可能不相关,提高特征的有效性和分割性能。本文选用Daubechies4基小波^{[ 6]}。小波分解各通道内不同纹理区域间的特征分离,还需要对小波系数作进一步纹理特征测度。由于低频信号承载了影像的近似信息,即纹理影像的轮廓结构信息,因此对小波分解的低频系数,采用窗口内小波系数的均值作为概略特征,可以最大程度保护纹理区域的边缘信息。高频信号承载影像的细节信息,即纹理影像的微观纹理信息,对高频系数,采用窗口内小波系数的标准差为纹理特征,可以最大程度突出微观纹理细节的变化频率信息。均值和标准差计算窗口采用(2 n₁ +1) ×(2 n₁ +1)。此外,对高频特征,可以在标准差基础上,再做进一步平滑计算,加强细节纹理间的紧致性^{[ 6]},平滑计算窗口采用(2 n₂ +1) ×(2 n₂ +1)。

一些文献分别证明了均值漂移算法对连续与离散函数的收敛性^{[ 7, 8]}以及收敛的充分条件^{[ 9]}。文献[9]成功地将其应用于影像分割、影像平滑问题后,其在影像滤波、边缘提取和信息融合等影像处理的多个领域也得到成功应用。文献[9]采用式(2)进行迭代计算:

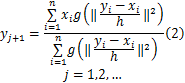
式中: y_j+1是第 j次迭代得到的特征状态; x是当前点,是与 y_j最接近的特征状态,即带宽内数据点中心。

文献[9]证明,当满足一定条件时,序列 y_j+1能够收敛到 y',则 y'点被称为数据中心 x对应的模式。均值漂移技术应用的复杂性在于它依赖两个相互关联的控制参数:带宽 h和密度 T^{[ 8]}。实际影像的离散特征空间密度表面一般不平滑,非均匀离散数据的密度统计与带宽选择密切相关^{[ 8, 9, 10]},带宽过大,会产生概括性过强的密度模式失真;带宽过小,在稀疏数据区域极易产生密度孤岛等过于琐碎的密度模式,使算法陷入局部极大。因此,利用较小带宽并附加密度约束是比较可靠的方法^{[ 8]},密度约束不仅可以避免无意义的模式判断过程,而且可以提高聚类精度、加速收敛。

在影像处理问题中,除变换的特征空间之外,每个像素点的空间信息也很重要。因此,有必要把影像的空间信息加入特征向量组中,这时,核函数如下:

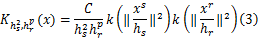
式中: x^r为空间位置特征; x^s为构成特征空间的特征向量; h_r和 h_s分别为空间带宽和特征带宽,空间带宽在影像中的取值窗口为 h_r=(2 n_r+1) ×(2 n_r+1); C是归一化常数。

带宽选择的困难在于统计密度模型的窄小峰值和细节变化与带宽有关。文献[11]提出两个自适应方案:一种是非参数法,需要定义新的均值漂移自适应过程,采用插入规则和抽样点密度估计算子;另一种是半参数法,采用局部数据结构抽取尺度信息。自适应带宽选择聚类优于固定带宽方法,但是,一方面加大了均值漂移计算代价,另一方面影像特征空间的复杂性很难被插入规则和结构信息所适应。因此,综合来看,文献[8]提出的峰谷比方法更加可靠且实用,但是,峰谷比的计算需要建立密度表面模型,增加了额外计算负担。基于以上的分析,本文提出了约束均值漂移(Constrained mean shift,CMS)方法,以解决复杂特征空间均值漂移的稳健性问题,带宽约束信息来自尺度传递的特征合并信息,无需任何额外计算。

从式(2)可看出,常规均值漂移算法必须假设数据密度的平滑性^{[ 9]},在离散数值影像中,假设密度平滑就是给出一个密度变化率限制,例如,图1中的蓝色散点,很容易获得一个平滑特征空间,常规均值漂移算法可以顺利实施。但是,图1中的红色散点,支离破碎、间断、阶梯状不平滑,很难获得一个平滑特征空间,因此,式(2)或式(3)所要求的路径连续性被破坏,常规均值漂移算法很难在这种特征空间中实施。为研究约束均值漂移(CMS)算法,应该讨论造成特征空间不平滑的成因,从而有针对性地提出路径约束条件。

研究表明文献[6]的特征传递方法是造成特征空间不平滑的原因,下面简要介绍其原理^{[ 6]}:如果窗口中不包含影像边缘,就使用较大的特征分析窗口进行分割;如果含有边缘,则缩小窗口,直至其中不再包含任何边缘为止^{[ 12]}。该思想可以通过搜索当前窗口的初分割邻域性质实现,即如果当前窗口和其邻域窗口在粗尺度特征空间中的分割结果都被分为同一类,那么就认为该窗口内不包含边缘并进行标记,否则不标记。这里,未被标记的区域就认为其中包含影像边缘,即为不同纹理间的交界区,对此再使用更细尺度的特征对其进行分割。也就是说,特征分析窗口的大小由其上一级分割的区域一致性及其邻域特性决定。小波系数特征满足马尔可夫性质,即当前窗口的性质只取决于其邻域窗口性质,而与其他窗口无关。所采用正交小波分解得到的每一尺度系数矩阵大小都是之前较细尺度系数矩阵的1/4,即每个小波系数都对应下一级的4个系数,相当于在下一尺度中把上一层特征窗口一分为四。具体分割过程,首先在小波分解的最粗尺度特征中应用均值漂移进行初分割并标记影像,然后把标记后的初分割结果扩展为原来的4倍,未标记区域使用其对应的较细尺度特征,而标记区作为一个整体使用相同分割区域内的特征均值作进一步分割, 直至得出最细尺度的分割结果。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 多尺度特征传递过程的特征分布示意图Fig.1 Feature distribution of multi-scale feature transfer plot

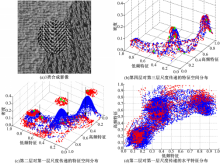
本文沿用文献[6]使用8邻域进行边缘判断搜索。为方便分析尺度传递前后特征空间变化情况,以3类纹理合成影像为例(见图1(a)),图解特征空间点的密度分布变化。图1中,蓝色为当前层通道的特征点,红色为接受上层通道特征传递后的特征聚类点,绿色点为聚类中心,聚类中心是上层小波系数聚类结果扩展4倍与对应下层均质区域特征值的平均值,边缘特征点保持不变。特征聚类空间由聚类中心和边缘特征点构成。图1(b)是第四层特征通道对第三层的特征传递的密度分布结果,由于第四层特征空间比较稀疏、绿色聚类中心点较多(20类),聚类比较分散,所以图1(b)中,红色散点相对于蓝色散点的间断性、阶梯状现象都比较轻微;但是,越向下层均值漂移的聚类数越接近实际类别,其特征传递效果越显著。图1(c)是第二层对第一层的特征传递结果密度分布,特征聚类空间的间断性、阶梯状非常显著。文献[6]通过多通道传递不同尺度特征,实现多尺度间的逐级选择性特征聚类,特征聚类空间隐含了尺度间的聚类信息,但是其平滑性被严重损坏,呈现间断性、阶梯状分布,见图1(b)(c)中的红色点。

尺度传递特征空间中包含两种点:聚类中心点和边缘点。一方面,离散点密度计算需要带宽假设,每个聚类中心密度的计算必然基于一定带宽范围,假设带宽足够小而不可能包含两个以上聚类中心,则聚类中心带宽范围内的近邻点必然是边缘点,同时,聚类中心密度主要是聚类中心对应的同类特征像素的重复计数构成,所以,其密度必然高于边缘点密度;同理,每个边缘点密度的计算也基于一定带宽范围,则与聚类中心较近的边缘点密度必然被聚类中心密度抬高,因此造成特征空间的阶梯状变化,并且影像区域的边缘一定处于特征空间阶梯变化的边缘,如图1(c)中黑色箭头所示。由于越向下层通道传递,聚类中心重复计数的基数越大,所以特征聚类空间的间断性、阶梯状现象越显著。另一方面,因为聚类中心是同类像素特征的重复(叠加)构成,因此特征聚类空间在水平方向的投影表现出伪稀疏化,加剧了水平方向的不连续性,见图1(d)中的红色点。

综上所述,在多尺度特征聚类空间(红色散点)应用常规均值漂移算法很难收敛到较高密度的优化模式,通过分析可以得出特征聚类空间的三个分布特点:①水平方向更加破碎、不连续;②密度方向(纵向)存在很大阶跃、不连续;③边缘点处于水平方向不连续和纵向阶跃的交界处。针对这3个特点,本文提出路径约束均值漂移(CMS)算法,既可利用尺度间的聚类信息又能够顺利实施均值漂移算法,在粗尺度聚类信息传递给细尺度的过程中,实现稳健聚类。

算法具体步骤如下:

Step1 均值漂移起点被约束为上层通道特征空间的聚类中心点(图1中绿色点)。用式(2)进行迭代计算时,当前点 x的第一个取值 x₁必须满足: x₁∈ Cet_Le,其中 Cet_Le是当前通道获得上层聚类信息后的聚类中心点的集合,下标 Le=3,2,1是金字塔层数,本文金字塔共分4层,顶层(即第4层)没有路径约束。 Cet_Le是聚类后新的特征空间的轮廓点,具有较高密度,均值漂移路径约束在 Cet_Le中,一致向更高密度特征点漂移,避免路径通过低密度区域,克服了数据不平滑导致的局部极大聚类错误,既缩短了收敛时间也排除了低密度聚类的发生。

Step2 迭代计算开始后, x_i为当前点,下标 i≥2,则密度模式满足 y₁ ii+₁…≤ y',当收敛到 y'后,开始新一轮迭代,重复Step1和Step2。均值漂移路径可以进入较高密度边缘点,形成新的聚类中心,不会落入较低密度边缘点,符合尺度传递特征。

Step3 给出恰当密度阈值,可以获得正确聚类模式,因为中间层具有较大聚类模式变动,没有模式收敛的意义,所以密度阈值 T只设置在最底层。密度阈值的选择具有经验性,但规律性很强,一般在密度突变位置附近就是密度阈值,取值范围较大且不敏感。

图2以密集城区影像提取树冠绿地为例,使用约束均值漂移进行实验,分别显示从粗尺度到细尺度的各小波分解层的聚类分割过程,可以看出,最终聚类结果如图2(e)所示,只在边缘处存在误差,总体效果较好。实验表明CMS方法在一定带宽范围内,对带宽变化不敏感,鲁棒性好。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 约束均值漂移方法各尺度层聚类分割过程Fig.2 Segmentation process of clustering at different scales by constrained mean shift method

应用多通道、多尺度均值漂移聚类进行纹理分割,依赖于多尺度特征传递的一致性以及各通道特征分布的可分性。应该指出,应用小波多尺度方法进行纹理分割,存在如下固有技术缺陷:①小波特征提取的下采样技术,导致最细尺度通道为原始影像空间尺寸的1/4,因此其分割结果与原始影像空间分辨率相差1/4像素;②特征聚类的精确性依赖于特征空间的可分性,小波特征提取很难保证纹理特征空间完全可分,特征的混淆性难以避免,纹理边缘错分割是原始影像的4倍。

纹理分割的关键困难在于纹理抽样与类别确定,CMS技术有效解决了纹理类别确定与纹理抽样问题。本文将CMS聚类作为纹理粗分割结果,利用影像空间纹理特征(或变换特征),提出基于聚类特征的监督分割方法,进一步细化边缘分割。原理与步骤如下:

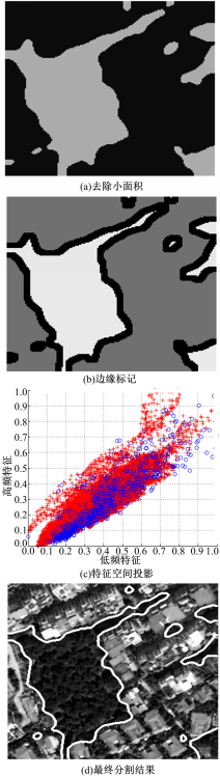
Step1 抽样影像准备:由均值漂移聚类的分割结果,可以确定纹理类别数,去除小面积并将聚类影像扩展4倍,得到与原始影像等尺寸的聚类影像,称为抽样影像,小面积去除的邻域窗口尺寸为(2 n_E+1) ×(2 n_E+1)。如图3(a)是对图2(e)去除小面积后的结果。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 基于聚类特征的监督算法原理Fig.3 Algorithm principle of feature supervision based on clustering

Step2 边缘标记,待识别像素准备:抽样影像中,存在边缘分割错误,利用文献[6]的标记原理,进行8联通标记,将窗口内不存在边缘的像素进行标记(即保留分类结果),未标记(取值为0)的像素即为待识别像素,标记窗口尺寸为(2 n_L+1) ×(2 n_L+1)。如图3(b)是对图3(a)的标记结果。

Step3 样本特征提取:抽样影像的聚类区域是不规则形状,在标记影像的约束下,进行纹理特征计算,需要将其划分成互相不重叠的规则影像块,影像块抽样窗口尺寸为(2 n₃ +1) ×(2 n₃ +1),设聚类数为 L,每一类可以划分的窗口数为 W_{L, p},则抽样影像的总窗口数为 S_p= 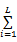W_{L, p},构成已分类像素纹理特征的计算单元,分别以低频均值和高频标准偏差为测度构成特征点,特征点数为 S_p,用以监督待识别像素的归属。如图3(c)中的蓝色点所示。

Step4 待识别像素特征提取:以待识别像素为中心,计算像素的纹理特征,特征计算窗口同抽样窗口,特征点数为待识别像素数。如图3(c)中的红色点所示。

Step5 监督计算:在特征空间中,计算待识别像素特征点(见图3(c)中的红色点)与样本特征点(见图3(c)中的蓝色点)之间的特征距离,取最小距离对应的样本特征点的属性类,赋予待识别像素。

Step6 影像分割:所有待识别像素计算完毕,将分类特征投影到影像空间,完成影像分割。

计算复杂度与待识别像素数、抽样特征点数有关。其中,待识别点数可以在均值漂移聚类阶段使其尽可能减少,抽样特征点数可以控制适度,同时,算法过程本质上可以实现并行计算,所以,在软件工程化实现中,计算效率可以保证。

实验一:为对CMS算法与常规MS算法的性能、精度、计算效率进行比较,本文采用4种人工合成纹理影像进行实验,并将标准模板与分割结果的边缘叠加在原始影像上进行目视对比,结果见图4。图4中黑色边界线是CMS方法的提取结果,白色边界线是MS方法的提取结果,红色边界线是标准模板。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 CMS算法与MS算法对比实验Fig.4 Contrast experiments between CMS algorithm and MS algorithm

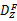
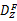
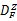
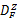
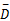
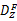
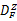
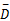
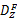
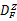
实验结果的评价可分成定性准则和定量准则两类。定性评价方法可结合应用和目视效果进行,定量评价方法分为基于区域的像素数量误差和基于边界的像素距离误差两种测度。为准确对比识别精度,本文同时采用了基于区域和边缘两种质量评价指标。以图4为例,CMS算法或MS算法提取结果的面积设为 M₁;标准模板是由人工确定的正确面积,设为 M₂;影像总面积设为 M。两者叠加之后,可以确定误分的像元范围及位置。1基于区域像素数量误差评价方法,是对比实验区的算法结果与模板面积的像素差异值,区域像素误分率 Err=|M₁ -M₂ |/M,则正确率 Cor=1 -Err。2基于边界的像素距离误差评价方法^{[ 13]},是用 F和 Z分别表示算法所得边界和模板边界,则 Z上各点到 F的最小距离和 F上各点到 Z的最小距离分别构成两个分布 和 ,它们的均值 μ 、 μ 和方差 σ 、 σ 可以用来度量 F和 Z之间的偏离,对均值和方差分别取平均值 μ =( μ +μ ) /2和 σ =( σ +σ ) /2,可以表示 F和 Z之间的综合偏离,单位为像素。数值越小则 F和 Z的吻合程度越高,即边界准确度就越高。

图4(a)(b)(c)(d)的实验参数和精度值列于表1。综合表1的定量指标与图4的定性观察来看,CMS算法的带宽选择敏感性显著下降,自动化程度大大提高;CMS算法与MS算法对纹理边缘分割的精度基本一致;CMS算法在特征空间中,通过继承较粗尺度特征通道的聚类信息,避免进行较低密度数据的无效搜索过程及其时间消耗,因此,聚类效率最大提高2.06倍,最小提高1.38倍,平均提高1.73倍。CMS的特点是:由于尺度传递造成特征空间复杂化,需要对均值漂移路径进行约束,因此CMS算法的路径约束思想是对MS在多尺度应用问题中的算法优化。对比实验表明,本文CMS算法的性能优于常规MS算法。

实验二:对高分辨率影像进行树冠提取。树冠提取研究的基本方法主要是基于光谱特征的各类方法,即便是使用高分辨率遥感影像,也主要是采用基于光谱特征的分类信息提取方法,均不能很好地解决树冠提取问题^{[ 14]},主要原因在于忽略了树冠在不同尺度下的纹理特征,因而光谱混淆不可避免。本文对高分辨率彩色影像采用基于光谱信息的直接监督和非监督方法进行树冠提取实验,与本文方法(仅采用光谱强度信息)进行实验对比,以验证本文算法对树冠提取的有效性。

选用城区树冠分布比较典型的高分辨率遥感影像进行提取实验,实验中采用了中国某地区0.5 m空间分辨率航空彩色影像数据,提取结果见图5~图7,图中黑色边界线包围的区域为计算机自动提取的城区树冠,白色边界线包围的区域为城区树冠的分割标准模板,由人工实测得到。图5是本文方法的结果,图5的实验参数列于表2,实验参数是通过特征空间分析启发式获得。图6是直接监督分类结果,图7是非监督分类结果。图6和图7算法均采用ERDAS软件进行实验,分割结果都进行了滤除小面积噪声的后处理,滤波窗口尺寸为9×9,相当于实地4.5 m²。实验结果的精度指标列于表3。

表1

Table 1

表1(Table 1)

表1 不同方法的对比实验结果 Table 1 Results of contrast experiments with different methods Image 带宽 计算 时间/s 基于区域/% 基于边缘/像素 Err/% Cor/% μ σ μ σ μ σ 图4(a) MS 变化 327.08 2.2 97.8 4.5 4.2 4.7 3.9 4.6 4.0 CMS 固定 176.78 2.3 97.7 4.6 4.2 5.2 4.6 4.9 4.4 图4(b) MS 变化 355.80 1.3 98.7 3.6 1.9 3.7 1.8 3.6 1.8 CMS 固定 220.20 1.8 98.2 2.5 2.1 3.5 2.7 3.0 2.4 图4(c) MS 变化 244.50 3.3 96.7 5.8 4.3 6.8 4.4 6.3 4.4 CMS 固定 176.61 2.7 97.3 4.6 2.7 5.4 3.0 5.0 2.8 图4(d) MS 变化 333.23 3.8 96.2 5.5 3.3 7.0 4.3 6.3 3.9 CMS 固定 162.05 4.1 95.9 5.7 3.8 7.2 4.4 6.4 4.1

表1 不同方法的对比实验结果 Table 1 Results of contrast experiments with different methods

由图5的提取结果总体可以看出,集中连片树冠提取效果较好,零星分散树冠较难提取,易被漏分;高大建筑之间的阴影对楼间较低矮树冠影响较大,易将阴影误分割成树冠,

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 本文方法典型城区树冠分布的提取实验结果(320×320)Fig.5 Extraction results for tree canopy in a typical urban area,processed by proposed method (320×320)

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 直接监督方法典型城区树冠分布的提取实验结果(320×320)Fig.6 Extraction results for tree canopy in a typical urban area,processed by direct supervised method(320×320)

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 非监督方法典型城区树冠分布的提取实验结果(320×320)Fig.7 Extraction results for tree canopy in a typical urban area,processed by unsupervised method(320×320)

所以,虽然本文方法获得了较好的效果,但是为简化模型中光谱描述难度,只考虑了光谱强度而没有考虑光谱矢量,所以在光谱识别上存在进一步扩展的空间。与图5相比,图6的提取结果中,误分割显著增加,主要原因是,在树冠光谱采样中,树冠阴影与树冠较难精确区分,在直接监督分割中建筑阴影与树冠阴影非常相似,从而导致大量误分割;同时,由于直接监督方法没有考虑多尺度与纹理因素,导致分割区域内部存在很多小斑块,经过后处理,依然存在较多破碎斑块。与图6相比,图7的提取结果中,误分割非常严重,主要原因是,非监督分割方法具有极大的盲目性,同时它也没有考虑多尺度与纹理因素,因此非监督分割基本是无效方法。定性分析认为,本文方法效果最优,直接监督方法次之,非监督方法基本无效。

结合对图5~图7的定性评价以及表3的定量分析可以得出如下结论:总体上,影响城区树冠识别率的因素包括:建筑物阴影、零星树冠与城市建筑物复杂环境的纹理背景相混合。总体精度表现为:树木植被越集中正确率越高,越零星分散正确率越低,建筑物遮挡越少正确率高,反之越低。提取方法的比较:直接监督分割方法只考虑了光谱多维矢量因素,而没有考虑尺度与纹理因素,其精度较本文方法低得多;非监督分割方法,既没有考虑光谱多维矢量的目标指向性,也没有考虑尺度与纹理因素,其错误率基本上都高于18.7%以上,其中图7(a)的错误率竟达到47.7%,所以直接使用非监督分割方法识别目标,基本上是无效的;本文方法在仅考虑光谱强度的情况下,提取精度最高,可见,在城市树冠提取中尺度与纹理因素是目标识别的主要因素。

表3中数据精度分析表明,本文方法自动提取城区树冠的正确率都在96%以上,平均正确率达到97.3%;基于边缘的平均均值偏差与平均方差偏差分别为6.1和7.4个像素,分别相当于实地3.1 m和3.7 m,可以满足城市绿量数据更新与城市快速发展情况下,绿化规模变化程度的客观评价、规划管理和环境保护等方面工作的实际应用要求。

表2

Table 2

表2(Table 2)

表2 图5的实验参数 Table 2 Experimental parameters of Fig.5 Image 层别 带宽 密度 特征窗口 监督分类参数 hs nr T/像素数 低频 n1 高频 n1 平滑 n2 nE nL n3 Fig.5(a) 4 0.05 1 1 1 3 1 2 2 6 3 0.05 2 1 3 3 1 2 0.08 3 1 3 3 3 1 0.08 4 1800 5 5 3 Fig.5(b) 4 0.05 1 1 1 3 1 1 1 6 3 0.05 2 1 3 3 1 2 0.08 3 1 3 3 3 1 0.10 4 2600 5 5 3 Fig.5(c) 4 0.05 1 1 1 3 1 2 2 6 3 0.08 2 1 3 3 1 2 0.08 3 1 3 3 3 1 0.10 4 2320 5 5 3 Fig.5(d) 4 0.05 1 1 1 3 1 3 3 6 3 0.08 2 1 3 3 1 2 0.08 3 1 3 3 3 1 0.10 4 2500 5 5 3

表2 图5的实验参数 Table 2 Experimental parameters of Fig.5

表3

Table 3

表3(Table 3)

表3 不同算法与实际量测结果的精度比较 Table 3 Precision comparison of different extraction algorithms and actual measured results Image 方法 基于区域(像素) 基于边缘(像素) Err/% Cor/% μ σ μ σ μ σ Fig.5(a) 本文方法 3.2 96.8 5.5 5.2 6.6 8.7 6.1 6.9 Fig.6(a) 直接监督 18.3 81.7 4.0 3.1 20.7 19.0 12.3 11.0 Fig.7(a) 非监督 47.7 52.3 10.3 6.4 23.2 16.6 16.7 11.5 Fig.5(b) 本文方法 2.3 97.7 4.7 4.7 7.3 13.2 6.0 8.9 Fig.6(b) 直接监督 10.9 89.1 3.8 4.6 12.6 15.8 8.2 10.2 Fig.7(b) 非监督 18.7 81.3 3.8 3.8 14.3 16.5 9.0 10.2 Fig.5(c) 本文方法 3.2 96.8 5.7 5.2 4.4 3.1 5.1 4.2 Fig.6(c) 直接监督 8.7 91.3 3.7 3.4 5.0 5.6 4.3 4.5 Fig.7(c) 非监督 22.5 77.5 7.3 6.2 9.0 8.4 8.1 7.3 Fig.5(d) 本文方法 2.2 97.8 10.0 15.8 4.6 3.1 7.3 9.4 Fig.6(d) 直接监督 9.7 90.3 4.9 4.9 9.0 11.6 6.9 8.3 Fig.7(d) 非监督 24.9 75.1 13.7 15.1 18.4 19.8 16.0 17.5

表3 不同算法与实际量测结果的精度比较 Table 3 Precision comparison of different extraction algorithms and actual measured results

本文提出了一种集光谱、纹理特征与多尺度分析方法于一体的树冠识别技术。首先根据树冠目标与背景之间在纹理和光谱强度两个方面的多尺度统计差异性,确定有效统计量,利用小波分解技术建立多尺度金字塔结构及其多尺度特征空间,然后利用尺度传递策略,采用约束均值漂移技术,从最粗尺度到最细尺度逐层聚类分割,实现多尺度树冠有效提取。实验表明,仅考虑光谱特征的非监督法基本上是无效方法,基于目标抽样的直接监督方法效果也不佳,本文方法取得了最好效果,表明算法具有良好性能与应用有效性。本文主要研究了同时顾及光谱、纹理和尺度的集成化树冠识别模型,为突出研究模型机理,减小模型描述难度,光谱特征只考虑了光谱强度信息,显然,如果引入多光谱或高光谱信息,纹理特征可以顾及多光谱纹理(如彩色纹理)描述,则可能获得更好的效果。