无级变速器电液控制系统关键技术

引用本文

韩玲, 张立斌, 安颖, 李春荣. 无级变速器电液控制系统关键技术. 吉林大学学报:工学版, 2014, 44(5): 1247-1252[HAN Ling, ZHANG Lin-bin, AN Ying, LI Chun-rong, Sohel Anwar. Key technology of the electric-hydraulic system for continuous variable transmission. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1247-1252] 复制到剪切板

Permissions

无级变速器电液控制系统关键技术

韩玲¹, 张立斌¹, 安颖², 李春荣³, Sohel Anwar⁴

1.吉林大学交通学院, 长春 130022

2.湖南大学汽车工程学院, 长沙 410000

3.吉林农业大学工程技术学院, 长春 130000

4.美国普渡大学机械学院, 印第安纳州 46202

通信作者:张立斌（1971-）,男,教授,博士生导师.研究方向:载运工具运用工程.E-mail:zlb@jlu.edu.cn.com

作者简介:韩玲（1984-）,女,博士研究生.研究方向:载运工具运用工程.E-mail:world-bird386@sohu.com

基金:国家自然科学基金项目(50775094)

摘要

针对无级变速器(CVT)电液控制系统软件开发过程中DNR离合器控制效果一致性的问题重点进行了分析。由于参数的多样性、不确定性和时变性导致了DNR湿式离合器开环控制存在一定难题,在分析其结合过程的基础上,针对半离合点和滑摩过程的控制提出了一种自学习方法。该方法将涡轮加速度作为目标,构建了李亚普诺夫判据的二次型性能方程,制定了学习规则,从理论上确保了自学习过程的渐进收敛性。为验证上述自学习控制算法在实际应用过程中的有效性,本文在ETAS软件中对上述控制算法进行了建模,并利用快速原型仿真工具对上述算法在实车上进行了测试,试验表明应用效果良好。

关键词: 汽车工程; 无级变速器; 电液控制系统; DNR湿式离合器

中图分类号:U472.9 文献标志码:A 文章编号:1671-5497(2014)05-1247-06

Key technology of the electric-hydraulic system for continuous variable transmission

HAN Ling¹, ZHANG Lin-bin¹, AN Ying², LI Chun-rong³, Sohel Anwar⁴

1.College of Transportation, Jilin University, Changchun 130022, China

2.College of Automotive Engineering, Hu'nan University, Changsha 410000, China

3.College of Mechanical Engineering, Jilin Agriculture University, Changchun 130000, China

4.College of Mechanical Engineering, Purdue University, Indiana 46202, USA

Abstract

The control consistency of Drive-Neutral-Reverse (DNR) clutch in the software development of the electric-hydraulic control system of Continuous Variable Transmission (CVT) is analyzed. The parameter diversity, uncertainty, and time-varying introduce difficulties to the open-loop control of DNR clutch. Regarding the filling time and the slipping process, a self-learning method is proposed, which takes the smooth turbine acceleration as the target. The learning rule is derived from the Lyapunov argument. The asymptotic convergence of the self-learning process is theoretically proved. To verify the effectiveness of the learning control algorithm in practical application, the control algorithm modeling is set up in the ETAS software, and the control algorithm is tested using rapid prototype simulation on real vehicle. The test results indicate that application effect of the control method is good.

Keyword: vehicle engineering; continuously variable transmission(CVT); electric-hydraulic control system; DNR clutch

Show Figures

0 引言

近些年来,许多学者对离合器的控制进行了研究,但研究对象往往是起步离合器,且认为带有液力变矩器作为起步装置的无级变速器离合器没有起步工况^{[ 1, 2, 3, 4, 5]}。鲜有人提及离合器在控制系统实际应用中的控制效果问题。但是在CVT实际应用的过程中,某些特殊工况下,即使带有液力变矩器,DNR通过前进档离合器和倒档制动器实现车辆的前进档(Drive)、空档(Neutral)和倒档(Reverse)之间的切换,离合器也会担负某种程度的起步功能^{[ 6, 7, 8, 9, 10]}。如将换档手柄切换到前进档时,在较短时间或几乎同时踩下加速踏板,此时离合器还处于充油或滑摩开始阶段,而发动机根据加速踏板信号已经提升功率,离合器的输入扭矩与转速提升,如没有相应的控制策略,会造成滑摩阶段离合器输入部件与从动部件滑摩不充分,在离合器结合过程的最后快速升压阶段,离合器输入部件与从动部件在仍有较大转速差的情况下突然结合,对传动系造成扭矩冲击,导致车辆起步时的冲击感,造成CVT的严重破坏。另外,如何在控制DNR离合器结合的过程中对离合器的充油过程、滑摩过程以及结合过程进行准确的控制,实现快速无冲击结合,也是要重点考虑的问题。因此为了提高离合器控制软件对诸多不确定性参数的适应性,本文对上述问题开展了相应的研究。

1 DNR离合器

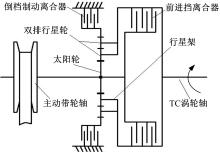
在配有液力变矩器的CVT车型上,DNR换向机构的典型结构如图1所示。

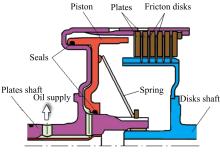
	Figure Option View Download New Window
	图1 DNR换向离合器原理简图Fig.1 Principle diagram of convert clutch

从图中可以看出:该DNR机构采用双排行星轮并配合前进档离合器和倒档制动离合器,通过调整制动离合器和前进档离合器的分离/结合状态来实现DNR档位的切换。前进档离合器和倒档制动器均采用液压执行元件,作用原理简图如图2所示。

	Figure Option View Download New Window
	图2 离合器结构原理图Fig.2 Principle diagram of the clutch

判断离合器结合性能的主要因素就是结合的平顺性(即冲击度)以及快速性(滑摩功)。

$\begin{matrix} \begin{matrix} J \frac{d ω_{cl}}{dt} = T_{cl} - T_{r} (1) \\ j = \frac{d^{2} ω_{cl}}{d t^{2}} = \frac{1}{J} (\frac{d T_{cl}}{dt} - \frac{d T_{r}}{dt}) (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} j \end{matrix}$ 为冲击度; $\begin{matrix} T_{cl} \end{matrix}$ 为作用在离合器从动盘上的扭矩; $\begin{matrix} T_{r} \end{matrix}$ 为整车各种阻力等效到离合器从动盘上的阻力矩; $\begin{matrix} J \end{matrix}$ 为离合器从动盘到车轮以及车辆的等效惯性。

在结合过程中 $\begin{matrix} T_{cl} \end{matrix}$ 油压 $\begin{matrix} P_{cl} \end{matrix}$ 的函数,假如 $\begin{matrix} d T_{r} / dt = 0, \end{matrix}$ 那么冲击度又可以表达为:

$\begin{matrix} j = \frac{1}{J} \frac{d T_{cl}}{dt} = \frac{1}{J} f' (P_{cl}) \frac{d P_{cl}}{dt} (3) \end{matrix}$

离合器油缸的压力可以表示为:

$\begin{matrix} \begin{matrix} \frac{d P_{cl}}{dt} = \\ \frac{E'}{V_{0, cl} + A_{cl} x_{cl} + C_{d, j} E'} (Q_{in} - Q_{leak} - A_{cl} {\overset{\cdot}{x}}_{cl}) (4) \end{matrix} \end{matrix}$

湿式离合器结合过程分为3个阶段,即快速充油阶段、滑摩阶段以及离合器结合阶段,3个阶段对应着离合器4种状态,用 $\begin{matrix} S_{cl} \end{matrix}$ 表示。

状态1: $\begin{matrix} S_{cl} = 0, \end{matrix}$ 离合器处于分离状态,此时的活塞在其初始位置 $\begin{matrix} X_{cl} = 0 。 \end{matrix}$ 对此时的离合器活塞进行受力分析有:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot \cdot}{X}}_{p} = {\overset{\cdot}{X}}_{p} = X_{p} = 0 \\ F_{p} = 0 \end{matrix} (5) \end{matrix}$

式中: $\begin{matrix} {\overset{\cdot \cdot}{X}}_{p} 、 {\overset{\cdot}{X}}_{p} \end{matrix}$ 和 $\begin{matrix} X_{p} \end{matrix}$ 分别为活塞轴向运动的加速度、速度以及位移; $\begin{matrix} F_{p} \end{matrix}$ 为作用在离合器活塞上的液压力。

状态2: $\begin{matrix} S_{cl} = 1, \end{matrix}$ 离合器处于快速充油阶段,活塞随着离合器油缸的充油而快速轴向移动, $\begin{matrix} 0 \leq X_{cl} \leq X_{\max} \end{matrix}$ 。对此时的离合器活塞进行受力分析有:

$\begin{matrix} \{\begin{matrix} m_{p} {\overset{\cdot \cdot}{X}}_{p} + C_{p} {\overset{\cdot}{X}}_{p} + k_{p} (X_{p} + X_{p 0}) = F_{cl} \\ F_{f} = 0 \end{matrix} (6) \end{matrix}$

式中: $\begin{matrix} F_{f} \end{matrix}$ 为作用在离合器摩擦片上的力;可以通过活塞面积和液体压强计算; $\begin{matrix} m_{p} \end{matrix}$ 为活塞质量。

状态3: $\begin{matrix} S_{cl} = 2, \end{matrix}$ 离合器建压阶段,此时的活塞已经到达其终止位置,即 $\begin{matrix} X_{cl} = X_{\max}, \end{matrix}$ 离合器摩擦片处于滑摩状态。

状态4: $\begin{matrix} S_{cl} = 3, \end{matrix}$ 离合器的从动片和主动片的速度差减小到一定程度,离合滑摩状态结束,离合器处于完全结合状态。

对状态3和状态4的离合器活塞受力状态进行分析有:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot \cdot}{X}}_{p} = {\overset{\cdot}{X}}_{p} = 0 \\ X_{p} = X_{p, \max} \\ F_{f} = F_{p} - k_{p} (X_{p, \max} + X_{p 0}) \end{matrix} (7) \end{matrix}$

式中: $\begin{matrix} k_{p} \end{matrix}$ 为离合器弹簧的刚度,文中将离合器弹簧的刚度视为定值。

经过上述分析,离合器的结合过程中其压力、离合器阀的控制目标以及离合器油缸充油的过程如图3所示。

	Figure Option View Download New Window
	图3 离合器结合过程示意图Fig.3 Structure diagram of the clutch process

图中在 t₁时刻,根据离合器油缸的压力响应计算公式可知,充油过程中离合器目标压力不直接影响离合器油缸的压力,而是影响离合器油缸的充油速度。因此, t₁过程中油缸压力与活塞行程近似呈线性比例关系。

t₁与 t₂时刻的过渡点A是充油结束的时刻,对这一过渡点的精确控制非常重要,否则会出现“充油过度”或者“充油不足”。“充油过度”,即在A点,离合器阀的目标压力继续保持 $\begin{matrix} P_{fill} \end{matrix}$ 不变,而离合器活塞到达其最大行程以后,进入油缸的流量会将离合器油缸内的压力水平快速提升至离合器阀的目标压力水平,引起换档冲击;“充油不足”,即充油尚未完成,控制系统已经将离合器阀的目标压力从 $\begin{matrix} P_{fill} \end{matrix}$ 拉低至 $\begin{matrix} P_{slip, 0}, \end{matrix}$ 导致充油速度下降,充油过程被拉长。如果在离合器油缸充满的时刻,离合器阀的目标压力已经沿着直线 $\begin{matrix} P_{slip, 0} - P_{slip, 1} \end{matrix}$ 将目标压力提升到较高的水平,那么作用在摩擦片上的压力也会在这一时刻迅速提升导致换档冲击。

$\begin{matrix} t_{2} 和 t_{3} \end{matrix}$ 时刻的过渡点B是离合器滑摩结束的时刻。在A这一点,控制系统将离合器阀的目标压力降低至较低水平 $\begin{matrix} P_{slip, 0}, \end{matrix}$ 这样作用于离合器油缸的压力就以这一较低的压力水平为起点,逐渐升高至 $\begin{matrix} P_{slip, 1} \end{matrix}$ 完成建压过程, $\begin{matrix} P_{slip, 1} \end{matrix}$ 是根据发动机的扭矩计算得到的。在这一过程中,离合器处于滑摩状态,作用在离合器从动摩擦片上的扭矩逐渐增大,从动摩擦片的转速与液力变矩器涡轮轴之间的转速差逐渐减小。滑摩结束之后,应立即将离合器阀的目标压力提升到较高水平 $\begin{matrix} P_{safe}, \end{matrix}$ 使得离合器的扭矩传递能力在发动机实际扭矩的基础上仍有一定的安全余量。

如果在滑摩结束之前将离合器阀的目标压力迅速提升,将会由于转速差的存在导致扭矩突变,从而引起第二次换档冲击。

综上所述,离合器结合的控制关键就在于精确控制A点和B点离合器油缸的压力变化。但是对于DNR离合器的开环控制系统,往往要耗费大量的精力对上述关键参数 $\begin{matrix} P_{slip, 0} 、 P_{slip, 1} 、 P_{safe} 、 P_{fill} 、 t_{1} 、 t_{2} \end{matrix}$ 及 $\begin{matrix} t_{3} \end{matrix}$ 进行测试标定,往往结果不尽如人意,原因就在于通过若干台标定车辆确定的控制参数无法较好地适应多变的工况、参数及各种影响因素。

影响离合器接合过程的因素多种多样,主要有:①驾驶员操作意图的随机性。②路况的复杂性。③离合器机械执行元件以及液压元器件的制造误差一致性。④离合器摩擦特性、电磁阀的电磁特性、油品参数等随着时间的衰减变化。因此,离合器控制的最大难点在于要搭建具有较强鲁棒性、具有高适应性的控制系统,并具有实际应用的可行性,基于上述要求,本文选择了自学习控制算法。

2 离合器自学习控制系统

2.1 充油阶段离合器自学习控制

根据图3所示离合器曲线,在离合器的充油阶段,电磁阀控制的目标压力 $\begin{matrix} P_{fill} \end{matrix}$ 保持不变,即离合器油缸充满且缓冲弹簧行程被完全压缩。半离合点的控制是整个过程中难度最大的点,离合器接合过程中的第一次冲击也来源于此。

充油过程的控制目标就是要以最快的速度充满油缸同时避免出现扭矩冲击。但是,在CVT变速器中,扭矩 $\begin{matrix} T_{cl} \end{matrix}$ 是无法测量的,当然也就不能被作为控制目标用于控制系统策略的设计。通过观察, $\begin{matrix} {\overset{\cdot}{T}}_{cl} \end{matrix}$ 的大小及变化率会直接引起涡轮转速 $\begin{matrix} ω_{t} 、 \end{matrix}$ 加速度 $\begin{matrix} {\overset{\cdot}{ω}}_{t} \end{matrix}$ 及加速度变化率 $\begin{matrix} {\overset{\cdot \cdot}{ω}}_{t} \end{matrix}$ 的变化,而与涡轮速度相关的参数是可以直接测量和计算的,因此可以将与涡轮转速相关的参数作为离合器控制器的控制依据。

在上述分析的基础上,针对离合器的充油过程设计了自学习控制器,结构如图4所示。

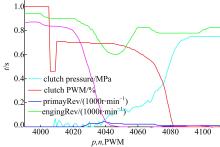
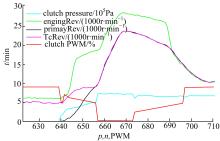
	Figure Option View Download New Window
	图4 具有自学习功能的离合器控制系统Fig.4 Clutch control system with self-learning function

图5为DNR离合器接合过程的一条典型曲线,从图中可以看出,离合器油缸的压力在目标时刻完成时并没有发生变化,而是在充油结束后的0.25 s后才开始上升,并且离合器压力开始上升的时刻,发动机转速和涡轮转速出现明显下降,由此判断,在充油阶段离合器存在充油不足的现象。

	Figure Option View Download New Window
	图5 离合器接合过程曲线Fig.5 The curve for clutch engagement process

2.2 滑膜阶段离合器自学习控制

由于冲击扭矩的不可测量性及其与涡轮转速的直接相关性,本文选择了涡轮转速参数作为自学习控制的依据。

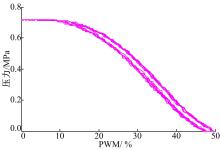
$\begin{matrix} \frac{d ω_{t}}{dt} = α_{1} T_{t} + α_{2} T_{cl} (8) \end{matrix}$

根据离合器电磁阀的试验特性曲线图6,取其类似线性的可控段,电磁阀的电流-压力特性表示为:

$\begin{matrix} P_{cl} = β_{1} I_{current, cl} + β_{2} (9) \end{matrix}$

	Figure Option View Download New Window
	图6 前进档离合器稳态调压Fig.6 Steady-state surge of f the forward gears cutch

要避免换档冲击的产生,液力变矩器涡轮转速 $\begin{matrix} ω_{t} \end{matrix}$ 的二次导数 $\begin{matrix} {\overset{\cdot \cdot}{ω}}_{t}, \end{matrix}$ 即加速度的变化率应当是稳定的,如果将某一常数作为 $\begin{matrix} {\overset{\cdot \cdot}{ω}}_{t} \end{matrix}$ 的控制目标,那么式(4)可以转换为计算目标驱动电流的公式:

$\begin{matrix} T_{cl} = λ_{1} P_{cl} + λ_{2} (10) \end{matrix}$

整理式(8)(9)(10)有:

$\begin{matrix} \begin{matrix} \frac{d ω_{t}}{dt} = α_{1} T_{t} + α_{2} [λ_{1} (β_{1} I_{current, cl} + β_{2}) + λ_{2}] (11) \\ I_{current, cl} = \frac{- α_{1} T_{t} - α_{2} λ_{2} + \frac{d ω_{t}}{dt}}{α_{2} λ_{1} β_{1}} - \frac{β_{2}}{β_{1}} = θ_{1} T_{t} + θ_{2} (12) \end{matrix} \end{matrix}$

参数 $\begin{matrix} θ_{1} \end{matrix}$ 和 $\begin{matrix} θ_{2} \end{matrix}$ 是不确定参数,而且具有时变性。从其推导过程可以看出, $\begin{matrix} α_{1} \end{matrix}$ 和 $\begin{matrix} α_{2} \end{matrix}$ 是有关旋转惯量和整车质量的参数, $\begin{matrix} β_{1} \end{matrix}$ 和 $\begin{matrix} β_{2} \end{matrix}$ 是与电磁特性以及液压系统增益相关的参数,而 $\begin{matrix} λ_{1} \end{matrix}$ 和 $\begin{matrix} λ_{2} \end{matrix}$ 则包含离合器弹簧刚度特性、离合器片摩擦特性及其随时间变化的不确定性等因素。自学习策略就是要解决其中包含的不确定因素,通过调整控制参数 $\begin{matrix} θ_{1} \end{matrix}$ 和 $\begin{matrix} θ_{2} \end{matrix}$ 来补偿系统特性的变化及其不确定因素。显然,通过自学习调整式(10)的参数可以解决系统的不确定性的问题。

将稳定涡轮加速度作为自学习控制目标,并为之设定一个允许范围:

$\begin{matrix} {\bar{α}}_{1} \leq |α_{t}| \leq {\bar{α}}_{u} (13) \end{matrix}$

由此,根据涡轮加速度的偏差范围,可以写出李亚普诺夫稳定性判据二次型性能方程:

$\begin{matrix} \begin{matrix} V (e) = e^{2} / 2 = (|α_{t}| - {\bar{α}}_{u})^{2} / 2, |α_{t}| < {\bar{α}}_{1} (14) \\ V (e) = e^{2} / 2 = (|α_{t}| - {\bar{α}}_{1})^{2} / 2, |α_{t}| > {\bar{α}}_{u} (15) \end{matrix} \end{matrix}$

在李亚普诺夫稳定性判据的基础上,应用链式法则,制定 $\begin{matrix} θ_{1} \end{matrix}$ 和 $\begin{matrix} θ_{2} \end{matrix}$ 的自学习规则:

$\begin{matrix} \overset{\cdot}{V} (e) = e \overset{\cdot}{e} = e \frac{\partial e}{\partial a_{t}} \end{matrix} \frac{\partial a_{t}}{\partial T_{c}} \frac{\partial T_{c}}{\partial P_{c}} \frac{\partial P_{c}}{\partial I_{current, cl}} \frac{\partial I_{current, cl}}{\partial θ} \overset{\cdot}{θ}$

式中: $\begin{matrix} θ = [θ_{1} {\begin{matrix} θ_{2} \end{matrix}]}^{T} 。 \end{matrix}$

结合式(8)(9)(10)并对其整理后代入上式(16):

$\begin{matrix} \begin{matrix} \overset{\cdot}{V} (e) = e \overset{\cdot}{e} = α_{2} β_{1} λ_{1} e [\begin{matrix} T_{t} & 1 \end{matrix}] [\begin{matrix} {\overset{\cdot}{θ}}_{1} \\ {\overset{\cdot}{θ}}_{2} \end{matrix}] = \\ - γ e ({\overset{\cdot}{θ}}_{1} T_{t} + {\overset{\cdot}{θ}}_{2}) (17) \end{matrix} \end{matrix}$

由于 $\begin{matrix} α_{2} < 0, β_{1} < 0 \end{matrix}$ 且 $\begin{matrix} λ_{1} > 0, \end{matrix}$ 因此自学习规则可以整理如下:

$\begin{matrix} {\overset{\cdot}{θ}}_{1} = γ_{1} e, {\overset{\cdot}{θ}}_{2} = γ_{2} e (18) \end{matrix}$

式中: $\begin{matrix} γ_{1} 、 γ_{2} \end{matrix}$ 为可调正增益,因此李亚普诺夫判据方程式是负定的,可以断定涡轮加速度的偏差的渐近稳定性是可以保证的,即当 $\begin{matrix} t \to \infty \end{matrix}$ 时, $\begin{matrix} e \to 0 。 \end{matrix}$

$\begin{matrix} \begin{matrix} \overset{\cdot}{V} (e) = - γe ({\overset{\cdot}{θ}}_{1} T_{t} + {\overset{\cdot}{θ}}_{2}) = \\ - γ (γ_{1} T_{t} + γ_{2}) e^{2} = - γ^{2} e^{2} < 0 (19) \end{matrix} \end{matrix}$

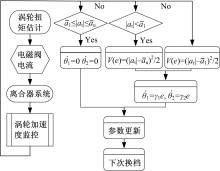
式(18)的物理意义在于:如果 $\begin{matrix} |α_{t}| < {\bar{α}}_{1}, \end{matrix}$ 即涡轮加速度太小将会导致滑摩时间过长,那么根据式(14)(16)有 $\begin{matrix} e = |α_{t}| - {\bar{α}}_{u} < 0, \end{matrix}$ 从而 $\begin{matrix} {\overset{\cdot}{θ}}_{1} < 0 \end{matrix}$ 且 $\begin{matrix} {\overset{\cdot}{θ}}_{2} < 0, \end{matrix}$ 在下一次的滑摩过程中控制参数将作负向调整,目的是使得涡轮的加速度斜率更大。反之,如果 $\begin{matrix} |α_{t}| > {\bar{α}}_{u}, \end{matrix}$ 即涡轮加速度过大,结合时间较短,那么根据式(14)(15)有 $\begin{matrix} e = |α_{t}| - {\bar{α}}_{t} > 0, \end{matrix}$ 从而 $\begin{matrix} {\overset{\cdot}{θ}}_{1} > 0 \end{matrix}$ 且 $\begin{matrix} {\overset{\cdot}{θ}}_{2} > 0, \end{matrix}$ 在下一次的滑摩过程中控制参数将作正向调整,使得涡轮的加速度斜率平缓,延长滑摩时间减少换档冲击。

根据上述分析,参数调整的自学习规则具有实际物理意义且易于实现,并且根据李亚普诺夫判据涡轮加速度的偏差具有渐进稳定性。将其应用于控制系统中的离合器控制模块,自学习模块的作用原理如图7所示。

	Figure Option View Download New Window
	图7 自学习控制模块原理图Fig.7 Principle diagram of the self-learning control module

3 离合器控制算法测试

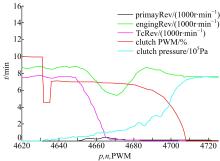
为验证上述自学习控制算法在实际应用过程中的有效性,本文在ETAS软件中对上述控制算法进行了建模,并利用快速原型仿真工具对上述算法在实车上进行了测试,测试结果如图8~图10所示。

	Figure Option View Download New Window
	图8 怠速工况离合器接合曲线Fig.8 Idle speed condition curve of clutch engagement

	Figure Option View Download New Window
	图9 节气门开度为中度时离合器接合曲线Fig.9 Throttle-opening medium level curve for clutch engagement

	Figure Option View Download New Window
	图10 节气门开度较大时离合器接合曲线Fig.10 Larger throttle-opening curve of clutch engagement

将图10与图5相比较可以看出,离合器油缸的压力在目标时刻完成时已发生变化,并且离合器压力上升后始终保持平稳状态,发动机转速和涡轮转速出现明显下降,由此判断,在充油阶段离合器充油充足,控制效果良好,通过对离合器接合过程的分析所建立的自学习控制模块达到了预期的控制效果。

4 结束语

参数的多样性、不确定性和时变性,导致了离合器接合一致性难以保证。本文在对离合器结合过程中的三个阶段进行了深入分析,针对不同阶段提出了不同的控制方案。对离合器充油过程,检测涡轮转速开始下降的时刻,并与目标充油结束时刻(即半离合点时刻)进行比较,然后根据两者之间的差值对目标充油时间进行调整。对离合器的滑摩阶段,监控其涡轮转速的加速度,以稳定的加速度值作为控制目标,构建了基于李亚普诺夫判据的二次型性能方程,并据此确定了自学习规则,确保了自学习控制过程的渐进收敛性。通过本文的研究,上述控制方案可进行工程化生产。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	高帅. 无级变速器电液控制系统开发及关键技术研究[D]. 长春: 吉林大学汽车学院, 2012. Gao Shuai. Development of the electric-hydraulic system for continuously variable transmission and research on the key technology[D]. Changchun: Automotive Engineering, Jilin University, 2012. [本文引用:1]
[2]	杨凯. 金属带式CVT夹紧力控制及液压控制系统的仿真分析[D]. 长沙: 湖南大学汽车工程学院, 2012. Yang Kai. The clamping force control and simulation analysis of hydraulic control system about Metal-Belt type CVT[D]. Changsha: College of Automotive Engineering, Hu'nan University, 2012. [本文引用:1]
[3]	张伯英. 金属带式无级变速传动机理与控制的研究[D]. 长春: 吉林大学汽车学院, 2002. Zhang Bo-ying. Study mechanism and control of metal belt continuously variable transmission[D]. Changchun: Automotive Engineering, Jilin University, 2002. [本文引用:1]
[4]	卢延辉, 张友坤, 郑联珠, 等. 基于Infenion C164CI的金属带式无级变速器电控系统设计[J] . 吉林大学学报: 工学版, 2006, 36(增刊): 84-88. Lu Yan-hui, Zhang You-kun, Zheng Lian-zhu, et al. Design of electronic control unit on infenion C164CI for metal belt continuously variable transmission[J]. Journal of Jilin University(Engineering and Technology Edition), 2006, 36(Sup. ): 84-88. [本文引用:1] [CJCR: 0.701]
[5]	张宝生, 付铁军, 周云山, 等. 金属带式无级变速传动系统与发动机的匹配及其控制策略[J]. 吉林大学学报: 工学版, 2004, 34(1): 65-70. Zhang Bao-sheng, Fu Tie-jun, Zhou Yun-shan, et al. Matching of V-belt type continuously variable transmission with engine and its control strategy[J]. Journal of Jilin University (Engineering and Technology Edition), 2004, 34(1): 65-70. [本文引用:1] [CJCR: 0.701]
[6]	周萍, 聂晋, 孙跃东. 基于模糊PID控制的CVT速比仿真研究[J]. 机械传动, 2011(8): 25-28. Zhou Ping, Nie Jin, Sun Yue-dong. Simulation study of CVT speed ratio based on fuzzy-PID control theory[J] . Journal of Mechanical Transmission, 2011(8): 25-28. [本文引用:1] [CJCR: 0.3404]
[7]	Togai K, Tamaki H. Human driving behavior analysis and model representation with expertise acquiring process for controller rapid prototyping[C]∥SAE Technical Paper, 2011-01-0051. [本文引用:1]
[8]	Prasad M, Sardar A, Mubashir S. Transmission technologies : an Indian perspective[C]∥SAE Technical Paper, 2011-26-0083. [本文引用:1]
[9]	Manyala J. Gearshift actuator dynamics predictions in a dual clutch transmission[J]. SAE Int J Commer Veh, 2013, 6(2): 589-597. [本文引用:1]
[10]	Kamijo S, Tomomatsu H, Sawada M, et al. Development of iQ with CVT for USA[J]. SAE Int J Engines, 2011, 4(1): 2142-2147. [本文引用:1]

2012

0.0

... 0 引言近些年来,许多学者对离合器的控制进行了研究,但研究对象往往是起步离合器,且认为带有液力变矩器作为起步装置的无级变速器离合器没有起步工况^[1,2,3,4,5] ...

2012

0.0

2002

0.0

2006

0.0

0.701

. 2006, 36(增刊):84-88

Design of electronic control unit on infenion C164CI for metal belt continuously variable transmission

利用单片机技术,基于C164单片机设计开发了金属带式无级变速器的电控单元,研究了控制系统的硬件及研究了输入模块和输出模块的设计原则.控制软件采用模块化设计思想,保证对系统进行实时优化管理.为了验证系统设计的正确性,进行了台架试验,结果表明,电控单元能完成控制要求并具有较好的控制效果.

2004

0.0

0.701

. 2004, 34(1):65-70

Matching of V-belt type continuously variable transmission with engine and its control strategy

College of Automotive Engineering, Changchun 130025, China

A fuel economy model was set up for the engine and on its basis the matching strategy for continuously variable transmission with the engine was studied and the relationship between engine goal rpm and vehicle speed was determined.The comprehensive control strategy was formulated from the demand on vehicle dynamic performance at transient operating conditions and fuel economy at steady operating conditions.The improved comprehensive control strategy remedies the deficiency of control strategy for best fuel economy,improves the vehicle dynamic performance at transient conditions without penalty on steady condition fuel economy.

建立了发动机燃油经济性模型,并在此基础上研究了发动机与无级变速传动系统的匹配策略,确定了发动机的目标转速与车速的关系。以实现汽车瞬态过程的动力性和稳态过程的经济性为依据,确定了综合控制策略。改进后的综合控制策略弥补了最佳燃油经济性控制策略的不足,提高了瞬态工况的动力性能,同时保持了稳定状态下系统的燃油经济性,改善了系统的性能。

0.0

0.3404

... 但是在CVT实际应用的过程中,某些特殊工况下,即使带有液力变矩器,DNR通过前进档离合器和倒档制动器实现车辆的前进档(Drive)、空档(Neutral)和倒档(Reverse)之间的切换,离合器也会担负某种程度的起步功能^[6,7,8,9,10] ...

0.0

2013

0.0

2011

0.0