汽车线束的动态串扰特性预测

引用本文

高印寒, 王天皓, 杨开宇, 张俊东, 樊宽刚, 朱宇. 汽车线束的动态串扰特性预测. 吉林大学学报: 工学版, 2014, 44(5): 1258-1263[GAO Yin-han, WANG Tian-hao, YANG Kai-yu, ZHANG Jun-dong, FAN Kuan-gang, ZHU Yu. Prediction of the dynamic crosstalk of automotive wiring hardness. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1258-1263] 复制到剪切板

Permissions

汽车线束的动态串扰特性预测

高印寒¹, 王天皓¹, 杨开宇¹, 张俊东¹, 樊宽刚², 朱宇³

1.吉林大学汽车仿真与控制国家重点实验室, 长春 130022

2.江西理工大学机电工程学院, 江西赣州 341000

3.吉林大学仪器科学与电气工程学院, 长春 130061

通信作者:杨开宇(1971-),男,副教授.研究方向:汽车电子、电磁兼容及车辆测试技术.E-mail:yangky@jlu.edu.cn

作者简介:高印寒(1951-),男,教授,博士生导师.研究方向:车辆测试技术及仪器.E-mail:yinhan@jlu.edu.cn

基金:高等学校博士学科点专项科研基金项目(20110061110059); 吉林省科技发展计划重点项目(20110326); 江西省教育厅青年基金项目(GJJ12353)

摘要

针对汽车线束中导线相对位置和线束对地高度参数以及由于不同的安装方式和汽车不同的运动状态带来的随机性,提出了一种在低频下用来计算汽车线束动态串扰的统计学模型。利用镜像法计算获得了带有绝缘层导线的单位长度分布参数,运用统计学原理推导得到了线束动态串扰的均值与方差,并将计算所得合理的最差串扰值与273次随机中点布置样条插值法(RDSI)仿真结果进行了对比,验证了模型的准确性和可靠性。所建立的线束动态串扰统计模型可以根据实际情况灵活调整相关参数,实现快速预测,为车辆电磁兼容性设计提供依据。

关键词: 车辆工程; 汽车线束; 串扰; 随机性; 统计模型

中图分类号:TM930.11 文献标志码:A 文章编号:1671-5497(2014)05-1258-06

Prediction of the dynamic crosstalk of automotive wiring hardness

GAO Yin-han¹, WANG Tian-hao¹, YANG Kai-yu¹, ZHANG Jun-dong¹, FAN Kuan-gang², ZHU Yu³

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

2.College of Mechanical & Electrical Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China

3.College of Instrumentation & Electrical Engineering, Jilin University, Changchun 130061, China

Abstract

Different installation methods and different moving states of automobile can bring randomness to the relative position of wire in automobile wiring harness and ground height of wiring hardness. A statistic model is proposed to calculate the dynamic crosstalk of automobile wiring harness under the low frequency. The image method is employed to acquire the unit length distribution parameters of the wire with insulation layer, and the principle of statistics is applied to infer the mean value and variance of the dynamic crosstalk of wiring harness. The reasonable worst-case crosstalk value calculated by the proposed model is compared with the 273 times simulation results of random displacement spline interpolation to verify the accuracy and reliability of the model. The proposed statistic model can also adjust the relevant parameters flexibly according to practical situation and realize rapid prediction, which provide the basis to the design of vehicle electromagnetic compatibility. The model has very important practical significance.

Keyword: vehicle engineering; automotive wiring harness; crosstalk; randomness; statistical model

Show Figures

0 引言

线束串扰已经成为汽车电磁干扰中最重要的传导干扰,同时也成为汽车电磁兼容设计的首要预测目标之一。线束串扰与导线在线束中的几何位置及对地高度等因素有关,但由于汽车线束在捆扎和固定的过程中具有不确定性,以及汽车在运动过程中存在振动、加速和减速等不同运动状态,使导线分布成为非确定性的几何布置,进而串扰也就具有了动态特性。因此,根据针对线束确定性几何布置的传统计算电磁学方法(如矩量法(MOM)、多导体传输线法(MTL)、时域有限差分法(FDTD)等)进行串扰分析,不仅会消耗大量的计算时间和计算机资源,而且生成的结果也并不理想。在导线串扰的动态预测研究中,国外学者已经获得了一定的成果,如分形理论^{[ 1]}、配置法^{[ 2]}、随机中点布置法^{[ 3]}、卷积法^{[ 4]}、随机中点布置样条插值法^{[ 5]}等。汽车线束对地高度和导线相对位置这两个因素的改变都会影响线束串扰的结果,其中国外的研究成果多数是针对导线相对位置变化对串扰的影响,而国内对汽车线束动态串扰的研究则刚刚起步,本文模型将同时考虑这两个因素变化时对汽车线束串扰产生的影响。

由于汽车线束几何布置和线束对地高度等因素的不确定性本质上是随机的,故采用统计模型对其串扰进行预测是最合适的。本文在假设导线无损耗、相互间弱耦合以及电小尺寸的条件下,利用镜像法获得等效电路模型的单位长度互电容和互电感,同时由于绝大多数的随机现象都服从或近似服从高斯分布,假设线束对地高度这个变量的概率密度函数符合高斯分布。在此基础上,运用统计学的方法获得导线相对位置及对地高度两个变量都发生变化时线束串扰的统计特性,并依此获得合理的导线串扰最差情况,最后通过与随机中点布置样条插值法(RDSI)^{[ 5]}仿真结果进行对比,说明本文提出的汽车线束动态串扰预测模型的可靠性。

1 线束选取及分布参数的确定

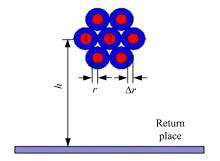
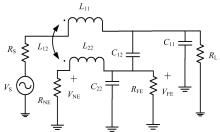
本文采用VW汽车电缆标准中的由7根18#规格导线组成的线束,线束中导体材料为铜,绝缘层是相对介电常数为 ε_r=3.0的PVC(聚氯乙烯),导线半径为 R=1 mm,其中导体半径为 r=0.5 mm,绝缘层壁厚Δ r=0.5 mm,线束长度为 L=2 m(电小尺寸),其结构如图1所示。从其中选取导线1为发射线,导线2为受扰线,发射线激励电压 V_S=1 V,源阻抗及终端阻抗分为高阻抗和低阻抗两种情况,分别为 R_S= R_L= R_NE= R_FE=50 Ω和 R_S= R_L= R_NE= R_FE=1 kΩ,因线束导线为电小尺寸、无耗弱耦合,可用如图2的三导体传输线串扰等效电路模型表示,其他导线的终端阻抗均设为50 Ω。

	Figure Option View Download New Window
	图1 2D线束横截面模型Fig.1 2D cross section of cable bundles model

	Figure Option View Download New Window
	图2 三导体传输线串扰等效电路模型Fig.2 Conductor transmission line crosstalk equivalent circuit model

由于假设导线无耗弱耦合,导致导线产生串扰的主要分布参数为单位长度的互电感和互电容^{[ 6, 7]},其中单位长度的互电感 $\begin{matrix} L_{mn} \end{matrix}$ 为:

$\begin{matrix} L_{mn} = \frac{μ_{0}}{4 π} \ln (1 + 4 \frac{h_{G} h_{R}}{s^{2}}) (1) \end{matrix}$

由于绝缘层的存在使导体周围介质不均匀,从而无法通过重要关系式 $\begin{matrix} LC = CL = εμ 获得单位长度的互电容 C_{mn}, \end{matrix}$ 不过本文利用镜像法原理推导获得了单位长度的互电容:

$\begin{matrix} \begin{matrix} C_{mn} = π ε_{0} C ([AB - \frac{1}{4} C^{2}]) (2) \\ 式中 : \\ A = (\frac{1}{ε_{r}} \ln \frac{1}{r_{a}} + ε_{e} \ln \frac{1}{r_{a} + Δ r_{a}} - \ln \frac{1}{2 h_{G}}); \\ B = (\frac{1}{ε_{r}} \ln \frac{1}{r_{b}} + ε_{e} \ln \frac{1}{r_{b} + Δ r_{b}} - \ln \frac{1}{2 h_{R}}); \\ C = \ln (1 + \frac{4 h_{G} h_{R}}{s^{2}}); \end{matrix} \end{matrix}$

$\begin{matrix} r 为导体半径; Δr 为导线绝缘层厚度; h_{G} 、 h_{R} 分别为发射线和受扰线的距地高度; s \end{matrix}$ 为发射线和受扰线之间的距离;有效介电常数 $\begin{matrix} ε_{e} = (ε_{r} - 1) / ε_{r} 。 \end{matrix}$ 通过式(1)(2)可以获得图1所示线束内处于不同相对位置的任意两导线间的单位互电感和单位互电容。

2 线束近端串扰的统计特性

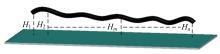
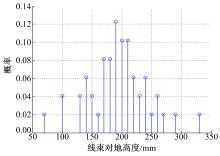
本文主要讨论的是线束对地高度和线束内导线相对位置两个因素都发生变化时线束的动态串扰特性,根据上述分析获得了线束内处于不同相对位置的两条导线的单位长度分布参数。此时假设线束对地高度变量的概率密度函数符合高斯分布^{[ 8, 9]},线束对地高度模型如图3所示。图4为随机产生的一组符合高斯分布的线束对地高度变量概率密度分布示意图,在本文动态串扰的计算模型中,线束对地高度变量可根据实际情况选取合适的均值和方差来描述符合高斯分布的概率密度函数。

	Figure Option View Download New Window
	图3 线束对地高度模型Fig.3 Height of cable bundles from ground level model

	Figure Option View Download New Window
	图4 线束对地高度的概率分布Fig.4 Probability distribution of the height of cable bundles from ground level

由于线束对地高度的概率密度函数可以根据实际情况进行确定,所以根据近端串扰的表达式^{[ 10]}:

$\begin{matrix} \begin{matrix} NEXT = |\frac{V_{NE}}{V_{S}}| = ω (M_{NE}^{IND} + M_{NE}^{CAP}) = \\ ω \frac{R_{NE}}{R_{NE} + R_{FE}} \frac{1}{R_{S} + R_{L}} l (L_{mn} + R_{FE} R_{L} C_{mn}) (3) \end{matrix} \end{matrix}$

可推导出不同线束对地高度下的串扰统计特性。其中, $\begin{matrix} M_{NE}^{IND} \end{matrix}$ 、 $\begin{matrix} M_{NE}^{CAP} \end{matrix}$ 分别为汽车线束近端串扰的感性耦合和容性耦合; $\begin{matrix} L_{mn} 、 C_{mn} \end{matrix}$ 为线束内发射线与受扰线之间的单位长度互电感与互电容值。

在实际汽车线束内发射线与受扰线的相对位置是沿着线束的长度方向具有不确定性的,因此为表现出这一实际特点,将线束划分为 $\begin{matrix} N_{S} 段, 其中每一段内被分析的两导线可选取线束内任意两条位置不同的导线, 其长度为 Δ l_{k}, k = 1,2, \dots, N_{S} 。 \end{matrix}$

$\begin{matrix} l = \overset{N_{S}}{\sum_{k = 1}} Δ l_{k} (4) \end{matrix}$

每段线束内导线的分布参数 $\begin{matrix} L_{mn} 、 C_{mn} \end{matrix}$ 是通过式(1)(2)计算获得的一对对应的相关随机变量。同时,线束对地高度变量的概率密度函数符合图3、图4的高斯分布模型。

将式(4)代入式(3)中得:

$\begin{matrix} \begin{matrix} NEXT = \\ ω \frac{R_{NE}}{R_{NE} + R_{FE}} \frac{1}{R_{S} + R_{L}} \sum_{k}^{=} (L_{mn} + R_{FE} R_{L} C_{mn}) Δ l_{k} (5) \\ 令 : P_{mk} = L_{mk} + R_{FE} R_{L} C_{mk} (6) \\ Δ l_{k} = \frac{x_{k}}{\overset{N_{S}}{\sum_{i = 1}} x_{i}} l (7) \end{matrix} \end{matrix}$

式中: $\begin{matrix} x_{k} (k = 1, \dots, N_{S}) 是在 (0, X) 内服从均匀分布的独立随机变量, X \end{matrix}$ 为任意正数。

从式(5)中可以看出,在 N_S被合适选取的情况下,导线在某一对地高度下的近端串扰值与角频率、负载阻抗和分段长度及该段内单位长度的互电感、互电容相关,其中每一段内的单位互电感和互电容具有一定相关性,应对应进行选取。将式(6)(7)代入式(5)中得:

$\begin{matrix} \begin{matrix} NEXT = ω \frac{R_{NE}}{R_{NE} + R_{FE}} \frac{1}{R_{S} + R_{L}} \overset{N_{S}}{\sum_{k = 1}} P_{mk} \frac{x_{k}}{\overset{N_{S}}{\sum_{i = 1}} x_{i}} l (8) \\ 令 : y = \overset{N_{S}}{\sum_{k = 1}} P_{mk} \frac{x_{k}}{\overset{N_{S}}{\sum_{i = 1}} x_{i}} (9) \end{matrix} \end{matrix}$

那么近端串扰的均值和方差可表示为:

$\begin{matrix} \begin{matrix} μ_{NEXT} = ω \frac{R_{NE}}{R_{NE} + R_{FE}} \frac{1}{R_{S} + R_{L}} l μ_{y} (10) \\ σ_{NEXT}^{2} = {(ω \frac{R_{NE}}{R_{NE} + R_{FE}} \frac{1}{R_{S} + R_{L}} l)}^{2} σ_{y}^{2} (11) \end{matrix} \end{matrix}$

式(9)中的 $\begin{matrix} P_{mk} \end{matrix}$ 和 $\begin{matrix} x_{k} \end{matrix}$ 是相互独立的变量, $\begin{matrix} P_{mk} = μ_{P_{mk}}, x_{k} = μ_{x_{k}}, 则基于泰勒级数展开的 y \end{matrix}$ 的均值和方差解析表达式为:

$\begin{matrix} μ_{y} = \end{matrix} y + \frac{1}{2} (\overset{N_{S}}{\sum_{k = 1}} \frac{\partial^{2} y}{\partial P_{mk}^{2}} σ_{P_{mk}}^{2} + \overset{N_{S}}{\sum_{k = 1}} \frac{\partial^{2} y}{\partial x_{k}^{2}} σ_{x k}^{2}) (12)$

$σ_{y}^{2} = \overset{N_{S}}{\sum_{k = 1}} [{(\frac{\partial y}{\partial P_{mk}})}^{2} σ_{P_{mk}}^{2} + {(\frac{\partial y}{\partial x_{k}})}^{2} σ_{xk}^{2}] (13)$

分别对 $\begin{matrix} y 求 P_{mk} \end{matrix}$ 和 $\begin{matrix} x_{k} \end{matrix}$ 的一阶偏导数及二阶偏导数:

$\begin{matrix} \frac{\partial y}{\partial P_{mk}} = \frac{1}{N_{s}} (14) \end{matrix}$

$\frac{\partial y}{\partial x_{k}} = \frac{\partial^{2} y}{\partial x_{k}^{2}} = 0 (15)$

$\frac{\partial^{2} y}{\partial P_{mk}^{2}} = \frac{\partial^{2} y}{\partial x_{k}^{2}} = 0 (16)$

将式(14)(15)(16)代入式(12)(13)得:

$\begin{matrix} \begin{matrix} μ_{y} = \frac{\overset{N_{S}}{\sum_{k = 1}} μ_{P_{mk}} μ_{x_{k}}}{\overset{N_{S}}{\sum_{i = 1}} μ_{x_{k}}} = μ P_{mk} (17) \\ σ_{y}^{2} = \overset{N_{S}}{\sum_{k = 1}} [{(\frac{1}{N_{S}})}^{2} σ_{P_{mk}}^{2}] = \frac{σ_{P_{mk}}^{2}}{N_{S}} (18) \end{matrix} \end{matrix}$

从式(17)(18)中可以看出,需要通过式(19)(20)计算获得 $\begin{matrix} P_{mk} \end{matrix}$ 的均值 $\begin{matrix} μ_{P_{mk}} \end{matrix}$ 与方差 $\begin{matrix} σ_{P_{mk}}^{2} 。 \end{matrix}$

$\begin{matrix} μ_{P_{mk}} = \end{matrix} μ_{lmk} + R_{FE} R_{L} μ_{c_{mk}} (19)$

$σ_{P_{mk}}^{2} = {(\frac{\partial P_{mk}}{\partial l_{mk}})}^{2} σ_{l_{mk}}^{2} + {(\frac{\partial P_{mk}}{\partial c_{mk}})}^{2} σ_{c_{mk}}^{2} +$

$2 \frac{\partial P_{mk}}{\partial l_{mk}} \frac{\partial P_{mk}}{\partial c_{mk}} σ_{l_{mk}} σ_{c_{mk}} ρ_{l_{mk}} c_{mk} (20)$

式中: $\begin{matrix} ρ_{l_{mk}} c_{mk} 为 l_{mk} 和 c_{mk} \end{matrix}$ 的相关系数。

由式(6)可知:

$\begin{matrix} \frac{\partial P_{mk}}{\partial l_{mk}} = 1; \end{matrix} \frac{\partial P_{mk}}{\partial c_{mk}} = R_{FE} R_{L} (21)$

将式(14)(15)(19)(20)(21)代入到式(10)(11)可得线束某一对地高度下近端串扰的均值和方差为:

$\begin{matrix} \begin{matrix} μ_{NEXT} = ω \frac{R_{NE}}{R_{NE} + R_{FE}} \frac{1}{R_{S} + R_{L}} \times \\ l (μ_{l_{mk}} + R_{FE} R_{L} μ_{c_{mk}}) (22) \\ σ_{NEXT}^{2} = ω \frac{R_{NE}}{R_{NE} + R_{FE}} \frac{1}{R_{S} + R_{L}} l \times \\ \frac{σ_{l_{mk}}^{2} + R_{FE}^{2} R_{L}^{2} σ_{c_{mk}}^{2} + 2 R_{FE} R_{L} σ_{l_{mk}} σ_{c_{mk}} ρ_{l_{mkcmk}}}{N_{S}} (23) \end{matrix} \end{matrix}$

利用式(22)(23),结合线束对地高度变量的概率分布,同时考虑汽车线束对地高度和导线相对位置两个变量,导线间的近端串扰值表达式为:

$\begin{matrix} μ_{c} = E \{C\} = \int μ_{\frac{c}{x}} P (x) dx (24) \end{matrix}$

式中: $\begin{matrix} μ_{c / x} \end{matrix}$ 为在线束对地高度概率分布中各个固定对地高度下的近端串扰的均值,可由式(22)求出; $\begin{matrix} P (x) \end{matrix}$ 为已知的与线束不同对地高度一一相对应的概率。

两个因素同时考虑时的串扰值方差可表示为:

$\begin{matrix} \begin{matrix} σ_{c}^{2} = E \{{(C - μ_{c})}^{2}\} = E \{C^{2}\} - μ_{c}^{2} (25) \\ 式中 : \\ E \{C^{2}\} = \int E \{\frac{C^{2}}{x}\} P (x) dx (26) \end{matrix} \end{matrix}$

某一固定对地高度下线束串扰的方差为:

$\begin{matrix} \begin{matrix} σ_{c / x}^{2} = E \{C^{2} / x\} - μ_{\frac{c}{x}}^{2} (27) \\ 所以有 : \\ E \{C^{2} / x\} = σ_{c / x}^{2} + μ_{c / x}^{2} (28) \end{matrix} \end{matrix}$

将式(28)代入式(26)可得:

$\begin{matrix} E \{C^{2}\} = \int (σ_{\frac{c}{x}}^{2} + μ_{\frac{c}{x}}^{2}) P (x) dx (29) \end{matrix}$

故式(25)可写成:

$\begin{matrix} σ_{c}^{2} = \int (σ_{\frac{c}{x}}^{2} + μ_{\frac{c}{x}}^{2}) P (x) dx - μ_{c}^{2} (30) \end{matrix}$

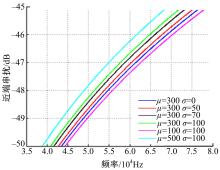
至此,同时考虑线束对地高度和导线相对位置两个变量的线束近端串扰统计特性参数 $\begin{matrix} μ_{c} 、 σ_{c} \end{matrix}$ 可由式(24)(30)获得。

3 基于统计特性的动态串扰最差情况预测

利用上述获得的线束近端动态串扰统计特性参数计算如图1所示的线束模型,其中令线束对地高度变量的概率密度函数是 μ=200 mm、 σ=100 mm的高斯分布,为了保证对动态串扰最差情况预测的合理性,选择置信水平为80%,此时所预测的线束动态串扰值80%都落入以均值 $\begin{matrix} μ_{c} \end{matrix}$ 为中心的 $\begin{matrix} \pm 1.25 σ_{c} \end{matrix}$ 范围内,故合理的最差情况近端串扰值为 $\begin{matrix} μ_{c} + 1.25 σ_{c} 。 \end{matrix}$ 进行对比的RDSI算法是对基于分形图学生成的线束随机性模型的改进,它不仅可以很好地表现出汽车线束分布的随机行为,而且更好地保证了线束具有良好的连续性^{[ 11]}。通过多次仿真可以形成线束串扰的动态变化区间,图5为不同负载阻抗下本文模型与RDSI算法计算结果的对比图。

	Figure Option View Download New Window
	图5 低阻抗负载和高阻抗负载近端串扰对比图Fig.5 Contrast figure of low impedance load and high impedance load near-end crosstalk

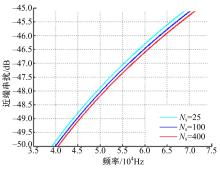
本算法应用到线束动态串扰预测的过程中具有相当高的灵活性,根据汽车内线束的真实情况,可通过调整线束对地高度的高斯分布概率密度函数和线束所分段数 $\begin{matrix} N_{S} \end{matrix}$ 来仿真实际情况,获得更加可靠的汽车线束动态串扰的预测结果,图6和图7分别表示低阻抗负载时,不同线束对地高度高斯分布概率密度函数和不同线束分段数 $\begin{matrix} N_{S} \end{matrix}$ 情况下线束近端动态串扰的仿真结果。通过仿真可知,当考虑线束的安装位置和车辆运动情况时,其全长各段的实际对地高度与预定高度离散程度越大,其近端串扰值越大。同时,在进行串扰计算时,将线束全长分割的段数越多,近端串扰值越小。

	Figure Option View Download New Window
	图6 不同对地高度模型近端动态串扰Fig.6 Near-end dynamic crosstalk of different above-ground-level models

	Figure Option View Download New Window
	图7 不同段数所对应的近端串扰Fig.7 Near-end crosstalk of different segments

4 结束语

在汽车运动和线束安装的过程中,线束内的导线相对位置和对地高度具有随机变化的特性,本文利用镜像法获得了具有绝缘层线束导线的单位分布参数,利用动态线束在低频下的统计特性获得了合理的最差情况近端串扰模型,通过与273次RDSI算法的仿真结果进行对比可知,在置信水平为80%的情况下,其在低频范围内的串扰值基本吻合,验证了模型的合理性和可靠性。同时,本文通过对实际的汽车线束建模,分析了该线束在不同的负载、线束对地高度分布及线束所分段数等情况下的近端动态串扰情况,说明了该模型的灵活性,能够结合汽车中线束的实际情况对相关参数进行调整,实现汽车线束动态串扰进行合理的快速预测。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Salio S, Canavero F, Lecointe D, et al. Crosstalk prediction on wire bundles by Kriging approach[C]∥2000 IEEE International Symposium on Electromagnetic Compatibility, Washington DC, USA: IEEE, 2000: 197-202. [本文引用:1]
[2]	Fatou D, Flavio C. Crosstalk statistics via collocation method[C]∥2009 IEEE International Symposium on Electromagnetic Compatibility , Austin, TX. United states: IEEE, 2009: 92-97. [本文引用:1]
[3]	Salio S, Canavero F, Lefkbvre J, et al. Statistical description of signal propagation on rand om bundles of wires[C]∥1999 International Zurich Symposium on Electromagnetic Compatibility, Zurich , Switzerland , 1999: 499-504. [本文引用:1]
[4]	Meilin W, Daryl G B, Todd H H, et al. Statistical prediction of “reasonable worst-case” crosstalk in cable bundles[J]. IEEE Transactions on Electromagnetic Compatibility, 2009, 51(3): 842-851. [本文引用:1] [JCR: 1.327]
[5]	Shishuang S, Geping L, Drewniak J L, et al. Hand -assembled cable bundle modeling for crosstalk and common-mode radiation prediction[J]. IEEE Transactions on Electromagnetic Compatibility, 2007: 708-718. [本文引用:2] [JCR: 1.327]
[6]	高印寒, 王瑞宝, 李碧若, 等. 汽车线束电感性串扰动态变化的预测[J]. 光学精密工程, 2011, 19(5): 1088-1094. Gao Yin-han, Wang Rui-bao, Li Bi-ruo, et al. Prediction of variation of inductive crosstalk in automotive cable bundles[J]. Optics and Precision Engineering, 2011, 19(5): 1088-1094. [本文引用:1] [CJCR: 2.239]
[7]	王瑞宝. 汽车线束分布参数和串扰预测研究[D]. 长春: 吉林大学仪器科学与电气工程学院, 2011. Wang Rui-bao. Reserch on prediction for parasitic parameters and crosstalk in automotive wiring harness[D]. Changchun: College of Instrument Science and Electrical Engineering, Jilin University, 2011. [本文引用:1]
[8]	Bellan D, Pignari S A. Estimation of crosstalk in nonuniform cable bundles[C]∥IEEE International Symposium on Electromagnetic Compatibility. USA: IEEE, 2005: 336-341. [本文引用:1]
[9]	Xiang L, Meilin W, Daryl G B, et al. Rapid simulation of the statistical variation of crosstalk in cable harness bundles[C]∥2010 IEEE International Symposium on Electromagnetic Compatibility. USA: IEEE , 2010: 614-619. [本文引用:1]
[10]	Paul C R. Introduction to Electromagnetic Compatibility[M]. 2nd ed. USA: Wiley Online Library, 2005: 402-421. [本文引用:1]
[11]	Fei D, Guihao B, Donglin S. Crosstalk prediction in nonuniform cable bundles based on neural betwork[C]∥2010 International Symposium on Antennas Propagation and EM Theory . Guangzhou, China: ISAPE, 2010: 1043-1046. [本文引用:1]

2000

0.0

... 在导线串扰的动态预测研究中,国外学者已经获得了一定的成果,如分形理论^[1]、配置法^[2]、随机中点布置法^[3]、卷积法^[4]、随机中点布置样条插值法^[5]等 ...

2009

0.0

1999

0.0

2009

1.327

0.0

2007

1.327

0.0

... 在此基础上,运用统计学的方法获得导线相对位置及对地高度两个变量都发生变化时线束串扰的统计特性,并依此获得合理的导线串扰最差情况,最后通过与随机中点布置样条插值法(RDSI)^[5]仿真结果进行对比,说明本文提出的汽车线束动态串扰预测模型的可靠性 ...

2011

0.0

2.239

. 2011, 19(5):1088-1094 DOI:10.3788/OPE.20111905.1088

Prediction of variation of inductive crosstalk in automotive cable bundles

1. Center of Test Science, Jilin University, Changchun 130022, China; 2. College of Instrumentation & Electrical Engineering, Jilin University, Changchun 130022, China; 3. Unit 92571 of the Chinese People's Liberation Army, Sanya 572021, China; 4. Research Institute of New Weaponry Technology ＆ Application, Naval University of Engineering, Wuhan 430033, China; 5. Special Information Department,Aviation University of Air Force, Changchun 130022, China

In order to predict the variation of inductive crosstalk in the cable bundles as the automobile was in motion, both the prediction model of the inductive crosstalk of the best/worst cases and the amended model by Monte Carlo method were established. According to the extreme positions of wires in the cable bundles, the prediction intervals of the inductive crosstalk of the best/worst cases were defined. By using the Monte Carlo method, the mathematical expectation of the inductive crosstalk was obtained, and the confidence interval for the expectation was defined under the circumstance of 80% confidence level. Here, the confidence interval was the amended prediction interval. By comparison with the results from EMC Studio electromagnetic simulation software, it is shown that the cable bundle crosstalks in all selected positions are in the best/worst case interval and most of them are in the amended interval when the frequencies are lower than 5 MHz.The length of the amended interval has decreased by 40%. Moreover,the electrical dimensions tend to electrically large and the error also increases when the frequencies are higher than 5 MHz.It concludes that the both models are simple and convenient to predict the inductive crosstalk rapidly according to different accuracy requests.

为了预测汽车运动时其线束的电感性串扰动态变化,建立了均匀、无损、弱耦合、电小尺寸线束的电感性串扰最好、最差情况预测模型和蒙特卡罗方法改进模型。根据导线在线束内几何布置的极限位置,得到电感性串扰的最好、最差情况预测区间;基于蒙特卡罗法得到电感性串扰数学期望值,在80%置信水平下求得期望值的置信区间,置信区间即为改进的预测区间。与EMC Studio仿真软件结果的比较显示,低于5 MHz时,所选位置的线束串扰都在长度为5 dB最好、最差预测区间内,多数位置线束串扰在长度为3 dB蒙特卡罗改进区间内,改进的预测区间缩小了40%;高于5 MHz时,电尺寸趋于电大,误差变大。建立的两个汽车线束电感性串扰预测模型能够根据不同精度要求快速预测电感性串扰动态变化。

... 由于假设导线无耗弱耦合,导致导线产生串扰的主要分布参数为单位长度的互电感和互电容^[6,7],其中单位长度的互电感 Lmn为: ...

2011

0.0

... 由于假设导线无耗弱耦合,导致导线产生串扰的主要分布参数为单位长度的互电感和互电容^[6,7],其中单位长度的互电感 Lmn为: ...

2005

0.0

... 此时假设线束对地高度变量的概率密度函数符合高斯分布^[8,9],线束对地高度模型如图3所示 ...

2010

0.0

... 此时假设线束对地高度变量的概率密度函数符合高斯分布^[8,9],线束对地高度模型如图3所示 ...

2005

0.0

... 由于线束对地高度的概率密度函数可以根据实际情况进行确定,所以根据近端串扰的表达式^[10]: ...

2010

0.0

... 进行对比的RDSI算法是对基于分形图学生成的线束随机性模型的改进,它不仅可以很好地表现出汽车线束分布的随机行为,而且更好地保证了线束具有良好的连续性^[11] ...