基于极值外推的高速列车齿轮传动装置载荷谱编制

引用本文

宫海彬, 苏建, 王兴宇, 徐观, 张益瑞. 基于极值外推的高速列车齿轮传动装置载荷谱编制. 吉林大学学报: 工学版, 2014, 44(5): 1264-1269[GONG Hai-bin, SU Jian, WANG Xing-yu, XU Guan, ZHANG Yi-rui. Compiling method of load spectrum of high-speed train gear drive system base on extreme value extrapolation. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1264-1269] 复制到剪切板

Permissions

基于极值外推的高速列车齿轮传动装置载荷谱编制

宫海彬^1,², 苏建¹, 王兴宇³, 徐观¹, 张益瑞¹

1.吉林大学交通学院, 长春 130022

2.上海汽车集团股份有限公司技术中心, 上海 201804

3.长春轨道客车股份有限公司技术中心, 长春 130062

通信作者:苏建(1954-),男,教授,博士生导师.研究方向:车辆智能化检测与诊断.E-mail:sujianjd@163.com

作者简介:宫海彬（1987-）,男,博士研究生.研究方向:车辆智能化检测与诊断.E-mail:gonghaibin126@aliyun.com

基金:吉林省科技发展计划项目(20080356); 长春市科技支撑计划项目(2010018)

摘要

针对传统传动系载荷谱编制时计数及统计方法的局限性及高速列车齿轮传动装置载荷测量的特殊性,构建了基于电机有功功率的高速列车齿轮传动装置扭矩间接测量方案,统计了传动系扭矩转数历程,提出了一种基于极值理论及非参数密度估计相结合的载荷数据统计方法,从而获得了总体载荷样本概率密度分布函数,并据此建立了高速列车齿轮传动装置程序载荷谱,实现了载荷极值外推和载荷谱压缩。最后,基于实测车辆网端功率转数历程完成了一个高速列车齿轮传动装置载荷谱编制算例。

关键词: 车辆工程; 载荷谱; 极值外推; 间接测量

中图分类号:U264 文献标志码:A 文章编号:1671-5497(2014)05-1264-06

Compiling method of load spectrum of high-speed train gear drive system base on extreme value extrapolation

GONG Hai-bin^1,², SU Jian¹, WANG Xing-yu³, XU Guan¹, ZHANG Yi-rui¹

1.College of Transportation,Jilin University, Changchun 130022, China

2.SAIC Motor Technical Center, Shanghai 201804, China

3.CNR CRC Technical Center, Changchun 130062, China

Abstract

For the limitations of traditional counting and statistic methods in drawing up load spectrum and the particularity of high-speed train gear drive load measurement, an indirect measurement scheme of torque of high-speed train drive system is proposed based on motor active power. Statistic calculation of the torque-revolution history of the gear drive system is carried out. Synthesizing extreme value theory and non-parametric probability density estimation, a load data statistical method is introduced. The probability density function of the overall load samples is obtained, and load extreme extrapolation and load spectrum compression are realized. Accordingly, high-speed train gear transmission unit's load spectrum is established. A case study based on measured network end power of rolling stock is presented to verify the proposed scheme.

Keyword: vehicle engineering; load spectrum; extreme value extrapolation; indirect measurement

Show Figures

0 引言

车辆在轨道上行驶时,高速列车齿轮传动装置处于高速重载的运行工况,校核其疲劳强度是否满足机车运用要求,对提高机车车辆的可靠性有重大意义。载荷谱的编制是进行疲劳寿命分析和疲劳可靠性试验的关键^{[ 1]}。根据实测或仿真获得的载荷时间历程编制传动系载荷谱时,往往采用能够较好反雨流计数法进行统计分析。如Xu等^{[ 2]}采用较好雨流计数法对装载机传动系载荷数据进行计数,基于非参数法进行统计外推,从而编制载荷谱。Kim等^{[ 3]}根据变速器输入轴的扭矩历程,采用雨流循环计数方法统计载荷循环分布并据此建立农用拖拉机传动系载荷谱。张英爽等^{[ 4, 5]}采用雨流计数法对传动系载荷历程进行统计处理,获得载荷均值和幅值的二维联合分布概率密度函数,并据此建立二维载荷谱。由于直接测试轮齿载荷较困难,传动系载荷测量时往往仅测量传动轴的扭矩,将载荷时间历程和相邻等值数据压缩,提取峰、谷值,然后采用雨流计数法提取循环数,然而该方法将无法反映载荷历程中相邻等值及幅值波动小的载荷对基于轮齿啮合传递扭矩的齿轮传动装置疲劳寿命的影响。同时,实测载荷数据有限,难以暴露全寿命周期可能发生对部件寿命影响较大的极值载荷。

针对高速列车载荷谱编制问题,本文提出一种基于能量转换法的高速列车传动系统扭矩测量的间接测量方法,根据获得的扭矩-转数分布构建一种基于极值理论与非参数密度估计相结合的高速列车齿轮传动装置载荷数据统计方法,以获得总体载荷样本概率密度分布函数,并实现载荷极值外推,据此完成高速列车传动系统载荷谱的编制。

1 扭矩测量方法

传动系统扭矩测量往往采用无线遥测的方法,高速列车传动系统布置十分紧凑,因此只能将应变片粘贴在联轴器表面,遥测系统发射机固定在联轴器上。但由于联轴器紧靠牵引电机,遥测系统必须解决牵引电机引起的电磁干扰问题,同时,高速列车传动系设计寿命十分长,线路试验所需测量里程相应较长,对测量系统的可靠性提出了很高的要求。

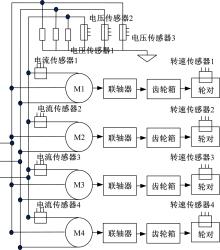
本文基于能量转换法提出适用于高速列车传动系统扭矩测量的间接测量方法,即采用电压传感器分别测量动车变流器输出三相电压,采用电流传感器测量各牵引电机单相输入电流计算得到的电机有效功率,以计算牵引电机输出扭矩。同时,将转速传感器安装在车轴轴箱盖上测量车轴转速。为测量每节动车4台电机的有功功率,构建的测量系统传感器布置如图1所示。电机每相有功功率为:

$\begin{matrix} P = \frac{1}{T} \int_{0}^{T} u (t) \times i (t) dt (1) \end{matrix}$

牵引电机 $\begin{matrix} i \end{matrix}$ 的输入有功功率为:

$\begin{matrix} P_{i} = \frac{3}{1000 \times T} \int_{0}^{T} u (t) \times i (t) dt (2) \end{matrix}$

牵引电机输出扭矩为:

$\begin{matrix} T_{m} = \frac{9549 η_{m} \cdot P_{i}}{r \cdot k} (3) \end{matrix}$

式中: $\begin{matrix} i (t) 为一相瞬时电流值; u (t) 为对应相位瞬时电压值; η_{m} 为电机效率; r 为车轴转速; k \end{matrix}$ 为齿轮箱传动比。

	Figure Option View Download New Window
	图1 电机有功功率测量传感器布置图Fig.1 Measuring sensor placement for traction motor’s active power measurement

由于测量高速列车传动系载荷时间历程进行的线路试验成本较高,而采用能量转换法在车辆实际线路运行时即可方便地进行试验测量,为获得传动系载荷时间历程提供了一个有效可靠的手段。

2 载荷数据统计方法

载荷数据统计是通过对实测载荷数据进行数据处理、概率统计,以获得代表全寿命周期载荷分布的概率密度函数,是载荷谱编制的关键。然而线路实测只能进行一定时间内的载荷时间历程的测量,不能够反映全寿命周期载荷分布,同时实测载荷包含大量不产生疲劳损伤的小载荷循环。

实测载荷数据统计包括无效载荷截除、载荷谱外推、载荷样本概率密度估计、极大值载荷截止等内容。其统计处理过程如下:①载荷数据预处理,获得齿轮传动装置的扭矩-转数分布图。②确定无效载荷门槛值,删除无效小载荷循环。③选取阈值,对大于阈值的载荷数据进行极值外推,以估计全寿命周期内可能发生的极大载荷数据,同时估计小于阈值的载荷数据的概率密度分布。④获得总体样本概率密度分布,确定载荷极值。

2.1 无效载荷的删除

载荷数据中包括大量不产生疲劳损伤的小载荷循环,为提高试验效率,必须删除小载荷循环,其中无效载荷门槛值的确定是关键。

高速列车齿轮传动装置具有较高的可靠性,通常其全寿命周期内载荷循环次数大于10⁹次,齿轮的疲劳破坏往往属于高周疲劳,疲劳极限对应的载荷循环次数为10⁷~10⁸。故选择累积频次为10⁸作为截至级,所对应的载荷值作为无效载荷门槛值 X_th。对于实测载荷信号,令 $\begin{matrix} D_{1} 为实测车辆行驶里程, D \end{matrix}$ 为设计寿命里程。则累积频次的截至级 N_th为:

$\begin{matrix} N_{t h} = 10^{8} \frac{D_{1}}{D} (4) \end{matrix}$

2.2 基于极值理论GPD分布的极值外推方法

载荷谱外推是依据样本推断全寿命周期内总体分布的未知部分。载荷历程中的极值载荷对部件损伤影响最大,而实测载荷仅能反映短期内的载荷历程,难以暴露全寿命周期可能发生的极值载荷。基于实测载荷数据的极值统计为准确估计极值载荷概率密度分布提供了一种有效方法。

为充分利用测量数据中包含的极值信息,可基于超出某阈值的载荷数据建立近似极值模型,即服从广义Pareto分布的超阈值载荷的概率密度分布。

2.2.1 超阈值载荷数据概率密度

如果 $\begin{matrix} X_{1} 、 X_{2} 、 \dots 、 X_{n} \end{matrix}$ 是一个独立同分布的随机变量,其分布函数为:

$\begin{matrix} G (x; μ, σ, ξ) = 1 - {(1 + ξ \frac{x - μ}{σ})}^{- 1 / ξ}, x \geq μ (5) \end{matrix}$

则称 $\begin{matrix} X \end{matrix}$ 服从广义Pareto分布,其中, $\begin{matrix} μ \in R 为位置参数, σ > 0 为尺度参数, ξ \in R \end{matrix}$ 为形状参数。

采用矩法、概率权矩法或极大似然估计法对Pareto分布参数 $\begin{matrix} μ 、 σ 和 ξ \end{matrix}$ 进行估计,从而获得超阈值载荷样本的概率密度分布函数。

2.2.2 阈值的选取

为正确估计广义Pareto分布 $\begin{matrix} G (x; μ, σ, ξ) 的参数, 首先要选择适当的阈值 u 。如果 u \end{matrix}$ 值选取过高,会导致超过阈值的样本个数太少,从而参数估计的方差会偏高。阈值的选取往往根据平均超出量函数法确定。

基于广义Pareto分布的平均超出量函数为:

$\begin{matrix} e (u) = E (X - u |X > u) = \frac{\hat{σ}}{1 - ξ} = \frac{σ + ξu}{1 - ξ} (6) \end{matrix}$

$\begin{matrix} e (u) 是 u 的线性函数, 对于给定的样本 X_{1} 、 X_{2} 、 \dots 、 X_{n}, \end{matrix}$ 样本平均超出量函数为:

$\begin{matrix} e_{n} (u) = \frac{1}{N_{u}} \sum_{i \in Δ_{n} (u)} (X - u), u > 0 (7) \end{matrix}$

式中: $\begin{matrix} Δ_{n} (u) = {i : X_{i} > u}; N_{u} \end{matrix}$ 为超出量的个数。

定义点集 $\begin{matrix} \{(u, e (u)) : u > 0}, 以 u 为横坐标, e (u) 为纵坐标, 绘制平均剩余寿命图。对于适当阈值 u_{0} > 0, 当 u > u_{0} 时, 样本平均超出量函数 e (u) 近似为线性, 斜率保持不变时, 通常可选取该点 u_{0} \end{matrix}$ 作为阈值。

2.3 阈值内载荷数据概率密度估计

实测载荷时间历程中阈值以内载荷数据概率密度分布形式是未知的,为掌握其密度分布,本文采用核密度函数估计法对其进行估计。

对于样本 $\begin{matrix} X_{1} 、 X_{2} 、 \dots 、 X_{n}, 定义一光滑函数 K (x) \geq 0 为核, 使 \int K (x) dx = 1, \int xK (x) dx = 0, 选择核函数 K, 给定带宽 h, \end{matrix}$ 定义核密度估计为:

$\begin{matrix} {\hat{f}}_{n} (x) = \frac{1}{n} \overset{n}{\sum_{i = 1}} \frac{1}{h} K (\frac{x - X_{i}}{h}) (8) \end{matrix}$

相应地,任意区间 $\begin{matrix} [a, b] \end{matrix}$ 内的概率为:

$\begin{matrix} \begin{matrix} {\hat{F}}_{n} (a \leq x \leq b) = \int_{a}^{b} {\hat{f}}_{n} (x) dx = \\ \frac{1}{\sqrt[]{2 π} n h} \overset{n}{\sum_{j = 1}} \int_{a}^{b} e^{- \frac{{(x - x_{j})}^{2}}{2 h^{2}}} dx (9) \end{matrix} \end{matrix}$

2.4 总体样本概率密度分布

根据选取的阈值,将实测载荷时间历程获得的载荷数据分为超过阈值的载荷样本和阈值以内的载荷样本两部分,其在总体载荷样本中的比例分别为 $\begin{matrix} K_{1} 、 K_{2} 。 \end{matrix}$ 根据广义Pareto分布获得超过阈值的载荷样本的概率密度分布 $\begin{matrix} g (x), 基于核密度函数估计方法计算阈值以内载荷样本的概率密度分布 f (x) 。 \end{matrix}$ 求得总体载荷样本概率密度分布及累积概率分布函数分别为:

$\begin{matrix} \begin{matrix} p (x) = \{\begin{matrix} K_{1} g (x), x \in [u, X_{\max}] \\ K_{2} \hat{f} (x), x \in [X_{t h}, u) \end{matrix} (10) \\ P (x) = \{\begin{matrix} K_{1} G (x), x \in [u, X_{\max}] \\ K_{1} + K_{2} \hat{F} (x), x \in [X_{t h}, u) \end{matrix} \\ (11) \end{matrix} \end{matrix}$

式中: X_max为载荷极大值。

已有研究和实践资料认为,10⁶个载荷循环对于很少发生的最严重情况在内的全部载荷具有足够的代表性。根据截除无效载荷后的载荷数据样本分布,选取10⁶个载荷循环累积频次为1的载荷作为载荷极大值 X_max,即:

$\begin{matrix} X_{\max} = X_{10^{- 6}} (12) \end{matrix}$

3 载荷谱编制及算例

3.1 高速列车齿轮传动装置载荷谱编制

程序载荷谱应在具有一定的精度的同时,保证试验简单便于实施,由于高速列车齿轮传动装置结构载荷或应力变化相对不太剧烈,其载荷谱可采用程序载荷谱描述。

结构平均使用寿命大于20个以上的程序块谱,能够较大地减少加载顺序对疲劳寿命的影响。考虑各程序块谱所需的加载时间,选择程序块循环次数为100,从而确定各程序块谱等效载荷频次为10⁶。将总体载荷样本的累积概率分布函数外推10⁶倍,即得载荷累积频次分布。本文选择8级程序载荷谱模拟传动系统工作载荷谱。

根据载荷极大值和无效载荷门槛值之间的载荷范围Δ X=X_max- X_min,常用的分级比例系数 $\begin{matrix} K = (X_{i} - X_{\min} \frac{)}{Δ} X \end{matrix}$ 分别为1、0.95、0.85、0.725、0.575、0.425、0.275、0.125。相应地,各载荷级 $\begin{matrix} X_{i} 的频次 Δ N_{i} \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} Δ N_{i} = \{\begin{matrix} N_{pi}, i = 1 \\ N_{i + 1} - N_{i}, i = 2,3, \dots, 8 \end{matrix} \\ (13) \\ N_{i} = \frac{1}{2} (N_{pi} + N_{pi - 1}) (14) \\ i = 2,3, \dots, 8 \end{matrix} \end{matrix}$

式中: $\begin{matrix} N_{pi} 为第 i \end{matrix}$ 级载荷的累积循环次数。

3.2 高速列车齿轮传动装置载荷谱编制算例

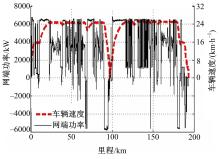
由于试验条件有限,目前尚未进行车辆运行时各牵引电机有功功率实测试验,本文基于如图2所示的某动车组型式试验时在某先导段进行典型运行图检查及能量消耗试验时测得的网端功率及车速历程两组实测数据编制载荷谱。将试验中上行和下行共运行193 km的两组数据作为一完整试验进行分析。

	Figure Option View Download New Window
	图2 网端功率及车速历程Fig.2 Power of network end and vehicle speed history

3.2.1 预处理

考虑车辆运行前、后车载电器消耗功率大致相同,可得牵引电机消耗(产生)的功率 $\begin{matrix} P_{z} \end{matrix}$ 为:

$\begin{matrix} P_{z} = P_{w} - P_{w 0} (15) \end{matrix}$

将牵引传动系统各部件功率因数、效率视为不随运行工况变化的常数,对各电机传递至传动系统的平均功率做近似估计,电机驱动状态时:

$\begin{matrix} P_{m} \approx P_{z} η_{tr} η_{conv} η_{inv} p_{m} η_{m} (16) \end{matrix}$

电机配合摩擦制动动力制动时:

$\begin{matrix} P_{m} \approx \frac{P_{z}}{η_{tr} η_{conv} η_{inv} p_{m} η_{m}} (17) \end{matrix}$

式中: P_w为实测网端功率; P_w0为未运行时初始网端功率; P_m为电机输出功率; η_tr=0.94,为牵引变压器效率; η_conv=0.975,为脉冲整流器效率; η_inv=0.985,为逆变器效率; p_m=0.87,为电机功率因数; η_m=0.94,为电机效率。

电机传递至传动系统的扭矩为:

$\begin{matrix} T_{m} \approx \frac{9549 \cdot P_{m}}{r} = \frac{9549 \times 3.6 \times 2 πR P_{m}}{60 vI} (18) \end{matrix}$

式中: $\begin{matrix} R 为轮对滚动圆半径; v 为车辆速度; I \end{matrix}$ 为齿轮箱传动比。

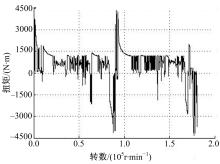
统计每转对应的电机输出扭矩,从而获得牵引电机输出扭矩-转数历程,如图3所示。保守考虑,将车辆制动时电机输出的负扭矩变成正扭矩。样本载荷最大值为 T_max=4467 N·m,根据截至级计算公式得 N_th=16 080,从而得无效载荷门槛值 T_th=1840.1 N·m。

	Figure Option View Download New Window
	图3 牵引电机输出扭矩-转数历程Fig.3 Motor output torque-revolution history

3.2.2 载荷数据统计分析及载荷谱编制

截除小于无效载荷门槛值的载荷,对剩余样本进行统计分析。根据前文所述方法计算样本超出量函数,并考虑超过阈值的样本个数,选取 u=4100,超过阈值的数据共528个,具体计算过程不在此赘述。样本参数进行极大似然估计 $\begin{matrix} (\hat{σ}, \hat{ξ}) = (176.14, - 0.4377), \hat{σ} \end{matrix}$ 和 $\begin{matrix} \hat{ξ} \end{matrix}$ 的标准误差分别为10.04和0.0414,可知超阈值样本服从ParetoⅢ型分布,具有有限的上端点。

分位数 x_p的估计为:

$\begin{matrix} {\hat{x}}_{p} = u + \frac{\hat{σ}}{\hat{ξ}} ({(\frac{n}{N_{u}} (1 - p))}^{- \hat{ξ}} - 1) (19) \end{matrix}$

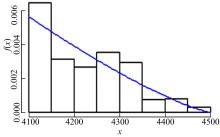
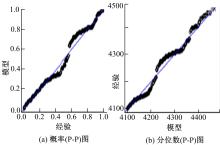
可得载荷样本上端点 $\begin{matrix} \hat{μ} = {\hat{x}}_{1} = 4502.4 。 \end{matrix}$ 由于载荷样本较少,包含极值信息较少,载荷极大值由4467 N·m外推至相应的4502.4 N·m,极值变化不大。相应地,求得超阈值样本的概率密度分布为:

$\begin{matrix} \begin{matrix} g (x) = \frac{1}{176.14} {(\frac{4502.4 - x}{402.4})}^{1.28} (20) \\ x \in [4100,4502.4] \end{matrix} \end{matrix}$

采用P-P图、Q-Q图对GPD模型拟合的载荷分布进行诊断,如图4所示,由于载荷数据不是完全独立同分布的随机变量,数据拟合效果并不是太好,但样本基本为一条直线,图5所示超阈值载荷的概率密度与直方图基本吻合,因此诊断图基本能支持所拟合的GPD模型。

	Figure Option View Download New Window
	图4 超阈值样本概率密度函数Fig.4 Probability density function of over-threshold sample

	Figure Option View Download New Window
	图5 GPD拟合诊断图Fig.5 Diagnostic diagram of GPD

采用核密度函数法估计低于阈值的15 552个样本数据分布,从而得到总体样本概率密度函数 $\begin{matrix} p (x) \end{matrix}$ 为:

$\begin{matrix} p (x) = \{\begin{matrix} 0.0328 g (x) = \frac{1}{5364} {(\frac{4502.4 - x}{402.4})}^{1.28}, \\ x \in [4100,4502.4] \\ 0.9672 {\hat{f}}_{n} (x), x \in [1840.1,4100) \end{matrix} (21) \end{matrix}$

相应地,总体样本的累积概率分布函数 $\begin{matrix} P (x) \end{matrix}$ 为:

$\begin{matrix} P (x) = \{\begin{matrix} 0.0328 G (x), x \in [4100,4502.4] \\ 0.0328 + 0.9672 \hat{F} (x), \\ x \in [1840.1,4100) \end{matrix} (22) \end{matrix}$

式中: $\begin{matrix} g (x) 、 G (x) 分别为超阈值样本的概率密度函数和分布函数; {\hat{f}}_{n} (x) 、 \hat{F} (x) \end{matrix}$ 分别为阈值内载荷样本的概率密度函数和分布函数。

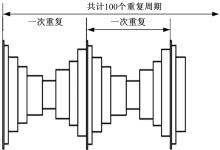
将总体样本的累积概率曲线外推10⁶倍得到相应的累积频次分布,采用8个块载荷按一定顺序排列组成一个块载荷程序,由100个重复的块载荷程序组成代表全寿命周期载荷历程的高速列车齿轮传动装置载荷谱。表1给出了一个块载荷程序中的块载荷水平及相应的循环次数,累积频次分布及相应的块载荷分布如图6所示。基于高速列车齿轮传动装置载荷历程分布特点确定高-低-高载荷排列顺序,制定的载荷谱见图7,至此完成了高速列车齿轮传动装置载荷谱编制算例。

表1 块载荷程序统计 Table 1 Statistics of block load

	Figure Option View Download New Window
	图6 累积频次及块载荷分布图Fig.6 Cumulative frequency and block load distribution

	Figure Option View Download New Window
	图7 高速列车齿轮传动装置载荷谱Fig.7 Load spetrum of high-speed train gear drive

通过数据处理和统计分析,截除了对部件损伤影响较小的载荷样本,载荷极大值由4467 N·m外推至4502.4 N·m,实现载荷极大值外推,同时验证了超阈值样本服从ParetoⅢ型分布,样本具有确定的极大值,符合实际车辆扭矩载荷状况。最后,根据实际车辆起动-加速-平稳运动-制动减速时齿轮传动装置扭矩载荷特点编制了高-低-高顺序的8级程序块载荷谱。该载荷谱能够较好地反映全寿命历程的高速列车齿轮传动装置载荷分布规律。然而由于采用基于车辆网端功率获得的传动系载荷历程与实际各电机输出扭矩尚存在一定区别,且试验样本较少,该载荷谱尚不能直接用于试验和设计。

4 结束语

针对高速列车齿轮传动装置载荷谱编制问题的特殊性,提出了具体的实施方案:①分析了高速列车齿轮传动装置扭矩测量的特点,构建了一种基于电机有功功率的高速列车齿轮传动装置扭矩间接测量方案。②提出了一种基于极值理论与非参数密度估计相结合的载荷数据统计方法,获得了总体载荷样本概率密度分布函数,实现了载荷外推,避免了测量周期载荷不包括全寿命周期中较少发生的极值载荷的问题。③根据总体载荷样本概率密度分布编制高速列车齿轮传动装置程序载荷谱,并基于实测车辆网端功率时间历程完成了一个高速列车齿轮传动装置载荷谱编制算例。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Berger C, Eulitz K G, Heuler P, et al. Betriebsfestigkeit in Germany—an overview[J]. International Journal of Fatigue, 2002, 24(6): 603-625. [本文引用:1] [JCR: 1.976]
[2]	Xu Zhi-qiang, Wang Hong-jian, Yao Ming-yao. Load spectrum compilation based on nonparametric statistical extrapolation[J]. Advanced Materials Research, 2013, 694: 271-277. [本文引用:1]
[3]	Kim Jung Hyeon, Kim Kyeong Uk, Wub Yong Gen. Analysis of transmission load of agricultural tractors[J]. Journal of Terramechanics, 2000, 37(3): 113-125. [本文引用:1] [JCR: 0.803]
[4]	张英爽, 王国强, 王继新, 等. 轮式装载机半轴载荷谱编制及疲劳寿命预测[J]. 吉林大学学报: 工学版, 2011, 41(6): 1646-1651. Zhang Ying-shuang, Wang Guo-qiang, Wang Ji-xin, et al. Load spectrum compiling and fatigue life prediction of wheel loader axle shaft[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(6): 1646-1651. [本文引用:1] [CJCR: 0.701]
[5]	刘永臣, 常绿, 孙丽. 轮式装载机传动系载荷谱编制方法研究[J]. 中国机械工程, 2012, 23(12): 1412-1416. Liu Yong-chen, Chang Lyu, Sun Li. A method of compiling load spectrum on wheel loader transmission[J]. China Mechanical Engineering, 2012, 23(12): 1412-1416. [本文引用:1] [CJCR: 0.751]

2002

1.976

0.0

. 2002, 24(6):603-625 DOI:10.1016/S0142-1123(01)00180-3

Betriebsfestigkeit in Germany—an overview

Abstract The German word “Betriebsfestigkeit” can be translated into English with several terms. The best expression seems to be structural durability or structural integrity. This article gives a brief description of the efforts taken especially by the German automotive industry and its cooperating research institutes to improve the accuracy of life time prediction and to optimise the proof-out by usage of experimental and numerical procedures. The advantages of standardised load–time histories (SLHs) for the user particularly in the pre design stage are shown and an overview of the existing SLHs is given. At the end of the article some aspects of practical applications of “Betriebsfestigkeit” in the German automotive industry are presented.

... 载荷谱的编制是进行疲劳寿命分析和疲劳可靠性试验的关键^[1] ...

2013

0.0

... 如Xu等^[2]采用较好雨流计数法对装载机传动系载荷数据进行计数,基于非参数法进行统计外推,从而编制载荷谱 ...

2000

0.803

0.0

. 2000, 37(3):null-null

Analysis of transmission load of agricultural tractors

... Kim等^[3]根据变速器输入轴的扭矩历程,采用雨流循环计数方法统计载荷循环分布并据此建立农用拖拉机传动系载荷谱 ...

2011

0.0

0.701

. 2011, 41(6):1646-1651

Load spectrum compiling and fatigue life prediction of wheel loader axle shaft

1.College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China|2.Research &|Development Center, China FAW Group Corporation, Changchun 130011, China|3.Technology Center, Liugong Machinery Co., Ltd, Liuzhou 545007, China

The load spectra of the wheel loader axle shaft were compiled by collecting the measured shaft load signals in the typical operation conditions to provide a reliable load condition for the prediction of the shaft fatigue life. Based on the compiled load spectra and the finite element analysis of the shaft, the fatigue life of the shaft was predicted using the Miner criterion. The effects of the operation conditions on the shaft fatigue life were analyzed. The results showed that the percentage of the fatigue damage is 68.6% in the operation in the cases of primary soil and semihumid soil, and it is less in other operation conditions. Considering the effect of the uncertainties on the fatigue life,the sensitivity analysis was performed on the shaft fatigue life. According to the sensitivity analysis result,the fatigue life increases by 3.7 times when the surface residual compressive stress reaches 100 MPa, and the fatigue life reduces by 80% when the load amplitude increases by 10%. The presented approach provides a reference for predicting the axle shaft fatigue life and improving its structural design.

通过实测装载机半轴典型作业工况的载荷信号，编制了半轴的载荷谱，为预测半轴疲劳寿命提供了载荷条件。根据所编制的载荷谱和半轴有限元分析结果，利用Miner准则对半轴进行了疲劳寿命预测。分析了不同工况对疲劳寿命的影响。结果表明：原生土和半湿土工况造成的疲劳损伤比例达到68.6%，而其他工况造成的损伤较小。考虑到不确定因素对疲劳寿命的影响，对半轴的疲劳寿命进行了灵敏度分析。由灵敏度分析结果可知，当半轴表面有100 MPa的残余压应力，可提高寿命3.7倍；载荷幅值增加10%，寿命减少80%。该方法可以为准确预测装载机半轴疲劳寿命，改进半轴结构提供参考。

... 张英爽等^[4,5]采用雨流计数法对传动系载荷历程进行统计处理,获得载荷均值和幅值的二维联合分布概率密度函数,并据此建立二维载荷谱 ...

2012

0.0

0.751

... 张英爽等^[4,5]采用雨流计数法对传动系载荷历程进行统计处理,获得载荷均值和幅值的二维联合分布概率密度函数,并据此建立二维载荷谱 ...