改进的湿式离合器带排转矩模型

引用本文

杨立昆, 李和言, 马彪. 改进的湿式离合器带排转矩模型. 吉林大学学报: 工学版, 2014, 44(5): 1270-1275[YANG Li-kun, LI He-yan, MA Biao. Improved drag torque model for wet clutch. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1270-1275] 复制到剪切板

Permissions

改进的湿式离合器带排转矩模型

杨立昆, 李和言, 马彪

北京理工大学车辆传动国家重点实验室, 北京 100081

通信作者:李和言（1978-）,男,副教授,博士.研究方向:车辆传动理论,摩擦与润滑.E-mail:Lovheyan@gmail.com

作者简介:杨立昆（1989-）,男,博士研究生.研究方向:传动装置功率损失特性.E-mail:maikiyang@gmail.com

基金:国家自然科学基金项目(51005021); 基础产品创新科研项目(VTDP-3203)

摘要

基于表面张力和表面波度以及摩擦副不平行度的影响,建立了改进的湿式离合器带排转矩模型。推导了考虑表面张力和表面湿润的摩擦副径向压力分布方程,同时推导了摩擦副不平行度和表面波度影响下的油膜厚度。通过计算研究发现:表面张力、摩擦副不平行度和表面波度均使离合器带排转矩增大,而且不平行程度越大,带排转矩增加越快,而表面波度对带排转矩的影响较小。将改进的模型与原模型和试验数据进行了对比,验证了改进模型的有效性。

关键词: 车辆工程; 湿式离合器; 带排转矩; 表面张力; 摩擦副不平行度; 表面波度

中图分类号:U463.22 文献标志码:A 文章编号:1671-5497(2014)05-1270-06

Improved drag torque model for wet clutch

YANG Li-kun, LI He-yan, MA Biao

State Key Laboratory of Vehicle Transmission, Beijing Institute of Technology, Beijing 100081, China

Abstract

An improved drag model for wet clutch is proposed based on the surface tension of lubricant, surface waviness and nonparallelism of friction pairs. The radial pressure distribution equation is derived by considering the surface tension and surface wettability. The thickness of oil film is deduced under the influences of surface waviness and nonparallelism of the friction pairs. Results of numerical calculation indicate that the surface tension, surface waviness and nonparallelism of friction pairs all lead to increase in the drag torque of wet clutch. The drag torque increases rapidly with rise of the nonparallelism, while the influence of the surface waviness is not obvious. The effectiveness of proposed model is verified by comparison of this model with existing model and with test data.

Keyword: vehicle engineering; wet clutch; drag torque; surface tension; nonparallelism of friction pair; surface waviness

Show Figures

0 引言

当前,采用湿式离合器的动力换档式变速箱在车辆上已获得广泛应用,而湿式离合器的带排损失也成为变速箱功率损失的主要成分,且具有不可消除性,不容忽视。有效减小湿式离合器的带排损失已成为提高变速箱效率的潜在措施,带排损失问题也成为动力换档变速系统设计中的研究热点。

对于湿式离合器带排损失的研究,国外主要从理论建模和试验研究两方面进行。理论建模的主要思路是通过分析离心力作用下的层流或紊流状态本构方程,建立摩擦副间油膜压力分布方程及带排转矩模型^{[ 1, 2, 3]}。同时,基于计算流体动力学(CFD)仿真分析表面沟槽对湿式多片式离合器带排转矩的影响^{[ 4, 5, 6]}。国内的研究方法与国外类似,主要基于黏性流体力学的层流理论及牛顿内摩擦定律建立带排转矩的预测模型,并进行相应的试验验证^{[ 7, 8, 9]}。文献[9]进一步考虑离合器主被动部分均有转速的情况,获得了油膜沿径向的压力分布方程以及带排转矩模型。但是,以上带排转矩模型的理论计算值和试验数据之间还存在一定偏差,理论模型大都忽略了以下两个方面的影响。首先,模型建立的基础是摩擦副工作在最理想的状态,未考虑摩擦副工作状态下的变化及表面几何形状的影响。此外,模型中未考虑表面张力和表面湿润的影响。润滑油和气体界面的表面张力使润滑油表面积趋于收缩,同时润滑油与摩擦副之间的湿润接触角也会使实际润滑面积发生变化,而且二者是相互关联的。在文献[3]的模型中虽引入了表面张力这一参量,但其分析存在一定的偏差。针对以上湿式离合器带排转矩研究的不足,本文建立了基于表面张力和表面湿润、摩擦副不平行度和表面几何形状的带排转矩模型,并进行了相应的仿真计算和试验对比验证。

1 考虑表面张力和表面湿润的带排转矩模型

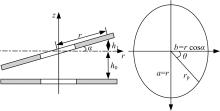
实际的车用湿式离合器的特点是多摩擦副、定流量润滑、主被动部分转速一般均不为0。在分离状态下其单摩擦副的简化几何模型如图1所示。

	Figure Option View Download New Window
	图1 湿式离合器摩擦副分离状态几何模型Fig.1 Geometric model of wet clutch friction pair during disengagement

文献[3,8-9]基于Navier-Stokes方程对相似的几何模型建立了摩擦副间润滑油的压力分布方程,并进行了相应的求解。当转速增大到一定值时,由于油膜的离心作用力,油膜产生边缘收缩作用,摩擦副不再处于全油膜润滑状态,油膜的实际作用半径会减小。

本文中,定义摩擦副等效外径为 $\begin{matrix} R_{e}, \end{matrix}$ 在离合器主被动部分转速均不为0的情况下推导得到的油膜等效外径内侧(不与空气接触一侧)与摩擦副内径处的压力差为:

$\begin{matrix} \begin{matrix} p (R_{e -}) - p (R_{i}) = \\ - (R_{e -}^{- 2} - R_{i}^{- 2}) \frac{27 ρ Q^{2}}{140 π^{2} h_{0}^{2}} - \frac{6 μQ}{π h_{0}^{3}} \ln (\frac{R_{e -}}{R_{i}}) + \\ (R_{e -}^{2} - R_{i}^{2}) \frac{ρ (3 Δ ω^{2} + 10 ω_{2} Δω + 10 ω_{2}^{2})}{20} (1) \end{matrix} \end{matrix}$

式中: $\begin{matrix} ρ \end{matrix}$ 为润滑油密度; $\begin{matrix} μ \end{matrix}$ 为润滑油黏度; $\begin{matrix} Q \end{matrix}$ 为润滑油供应流量; $\begin{matrix} h_{0} \end{matrix}$ 为名义油膜厚度; $\begin{matrix} ω_{2} \end{matrix}$ 为离合器主动部分转速; $\begin{matrix} Δω \end{matrix}$ 为主、被动部分转速差,应为负值。

在变速箱实际运行过程中,分离的离合器主、被动部分之间总保持确定的速比关系,则:

$\begin{matrix} Δω = \pm (ω_{1} - ω_{2}) = \pm ω_{2} \cdot (\frac{1}{i} - 1) (2) \end{matrix}$

式中: $\begin{matrix} i \end{matrix}$ 为主、被动部分速比。

在等效外径外侧(与空气接触一侧),由于液体表面张力的存在,油膜表面会产生压力波动^{[ 3, 10]}。同时由于固-液界面的自由能,为保证润滑油与空气接触部分表面积最小,摩擦副与润滑油的固-液界面的接触角变小,浸润面积增大^{[ 11, 12]},综合作用下的结果如图2所示,这些因素的作用对等效外径的大小产生影响。等效外径内、外侧的压力波动为:

$\begin{matrix} p (R_{e -}) - p (R_{e +}) = F_{σ} / A_{e} (3) \end{matrix}$

式中: $\begin{matrix} F_{σ} \end{matrix}$ 为润滑油表面张力; $\begin{matrix} A_{e} \end{matrix}$ 为润滑油表面积。

	Figure Option View Download New Window
	图2 摩擦副间油膜接触角分析模型Fig.2 Oil film contact angle model of friction pair

根据表面张力和表面湿润角的定义,取润滑油在摩擦副之间分布有表面张力的周线长为 $\begin{matrix} L, \end{matrix}$ 由图2分析则有:

$\begin{matrix} F_{σ} = σ \cdot L = σ \cdot 2 π \cdot \frac{h_{0}}{2} = πσ h_{0} (4) \end{matrix}$

式中: $\begin{matrix} σ \end{matrix}$ 为表面张力系数。

表面张力作用下的润滑油表面积为:

$\begin{matrix} A_{e} = (π - 2 φ) \cdot 2 r_{s}^{2} = \frac{(π - 2 φ) \cdot h_{0}^{2}}{2 co s^{2} φ} (5) \end{matrix}$

式中: $\begin{matrix} φ \end{matrix}$ 为固-液表面接触角。

将式(3)(4)(5)代入式(1),整理得:

$\begin{matrix} \begin{matrix} p (R_{e +}) - p (R_{i}) = \\ - (R_{e +}^{- 2} - R_{i}^{- 2}) \frac{27 ρ Q^{2}}{140 π^{2} h_{0}^{2}} - \frac{6 μQ}{π h_{0}^{3}} \ln (\frac{R_{e +}}{R_{i}}) + \\ (R_{e +}^{2} - R_{i}^{2}) \frac{ρ (3 Δ ω^{2} + 10 ω_{2} Δω + 10 ω_{2}^{2})}{20} - \\ \frac{2 πσ co s^{2} φ}{(π - 2 φ) h_{0}} (6) \end{matrix} \end{matrix}$

通常离合器的润滑流量是一定值,且入口与出口处压差较小,在一般情况下可忽略不计,从而由式(6)通过数值计算可获得摩擦副的等效外径。

根据牛顿内摩擦定律,作用在摩擦副上的切应力为:

$\begin{matrix} τ_{θz} = \frac{μΔωr}{h} (7) \end{matrix}$

式中: $\begin{matrix} h \end{matrix}$ 为实际油膜厚度; $\begin{matrix} r \end{matrix}$ 为径向坐标。

进一步求得单摩擦副时的带排转矩为:

$\begin{matrix} T = \int_{0}^{2} \int_{R_{1}}^{R_{e}} \frac{μ \cdot Δω}{h} r^{3} drdθ (8) \end{matrix}$

式中: $\begin{matrix} θ \end{matrix}$ 为周向坐标。

多摩擦副的带排转矩一般认为是单摩擦副带排转矩的线性叠加。

2 考虑摩擦副表面状态的油膜厚度

2.1 考虑摩擦副不平行度的油膜厚度

湿式离合器在工作过程中,由于外界随机扰动的存在,如润滑油压的不均匀作用以及花键的摩擦作用等因素使得摩擦片或对偶钢片出现一定的倾斜,即二者之间有一定的不平行度。假设摩擦片相对位置不变,对偶钢片偏离原位置角度为 $\begin{matrix} α \end{matrix}$ ,钢片上任意一点偏离初始位置为 $\begin{matrix} h_{1} \end{matrix}$ ,如图3所示。

	Figure Option View Download New Window
	图3 不平行状态下的摩擦副几何模型Fig.3 Geometric model of friction pair under nonparallelism condition

对偶钢片在标准位置的投影为椭圆,根据相应的几何投影关系,椭圆半长轴与半短轴长度如图3所示,进而半径的投影长度为:

$\begin{matrix} \begin{matrix} r_{p} = \frac{ab}{\sqrt[]{a^{2} co s^{2} θ + b^{2} si n^{2} θ}} = \\ \frac{rcosα}{\sqrt[]{co s^{2} θ + si n^{2} θco s^{2} α}} (9) \end{matrix} \end{matrix}$

所以钢片的偏离距离为:

$\begin{matrix} h_{1} = \sqrt[]{r^{2} - r_{p}^{2}} = \frac{rcosθsinα}{\sqrt[]{co s^{2} α + si n^{2} αco s^{2} θ}} (10) \end{matrix}$

则这种情况下摩擦副之间的实际油膜厚度为:

$\begin{matrix} h = h_{0} + h_{1} = h_{0} + \frac{rcosθsinα}{\sqrt[]{co s^{2} α + si n^{2} αco s^{2} θ}} (11) \end{matrix}$

将式(11)代入式(8)即可求得摩擦副不平行时的湿式离合器带排转矩值。

2.2 考虑摩擦副表面几何的油膜厚度

机械零件经加工制造产生的表面结构比较复杂,主要包括宏观形状误差和微观几何形状。对于离合器的摩擦副,宏观形状误差主要是表面波度。表面波度一般是周期性的,对于普通的加工方法,其波高范围最大可达500 μm^{[ 11]},一般情况下也在几十微米到100 μm左右,这样的幅值已与名义油膜厚度接近,对离合器摩擦副间带排损失会产生一定的影响。微观几何形状一般指表面粗糙度,不同加工方法下其粗糙度范围一般不同,但最大值一般为几微米,较摩擦副间隙小两个甚至多个数量级,所以其对带排损失的影响可忽略。一般表面波度的表征形式为^{[ 13]}:

$\begin{matrix} h_{2} = h_{n} \cos (nθ) (12) \end{matrix}$

式中: $\begin{matrix} h_{n} \end{matrix}$ 为表面波度幅值; $\begin{matrix} n \end{matrix}$ 为表面波度的数目,通常波峰之间的距离为0.8~10 mm。

考虑摩擦副表面波度的实际油膜厚度为:

$\begin{matrix} h = h_{0} + h_{2} = h_{0} + h_{n} \cos (nθ) (13) \end{matrix}$

3 模型求解与验证

为了验证上述分析的正确性与合理性,并验证本文模型是否较以往模型有所改进,将新模型的计算结果与文献[9]中所建模型的结果进行对比,并针对不同对偶钢片偏离角度和不同表面波度下的带排转矩进行分析。因为计算所得的带排转矩值相对较小,为使模型的计算结果能够体现出更明显的差异性以便于分析,需合理选取计算参数。根据润滑油的黏温特性,计算中选取润滑油油温为40 ℃。具体的摩擦副结构参数和润滑油相关参数如下:润滑油密度 ρ=875kg·m^-3,润滑油黏度 μ=0.086 Pa·s,表面张力系数 σ=0.035 N·m^-1,润滑油供应流量 Q_i=1.5 L·min^-1,摩擦片内径 R_i=86 mm,摩擦片外径 R_o=125 mm,名义油膜厚度 h₀=0.6 mm,摩擦副内外径压差Δ p=0 Pa,摩擦副数 Z=1,离合器主被动部分速比 $\begin{matrix} i \end{matrix}$ =1.8。

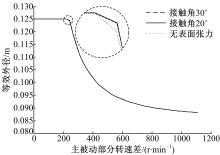
为分析表面张力对带排转矩的影响,分别取有表面张力和无表面张力两种情况进行计算,其中对于有表面张力时又分别取湿润接触角分别为20°和30°进行分析,在以上计算参数下,得到的等效外径与润滑油表面张力的关系如图4所示。可以看出,表面张力的存在使等效外径有所增大,

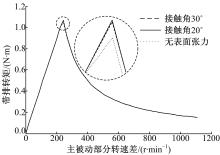
	Figure Option View Download New Window
	图4 表面张力对等效外径的影响Fig.4 Influence of surface tension on equivalent outer radius

且随着接触角的减小,等效外径的值也会变大。而离合器带排转矩与表面张力的关系如图5所示。可见,3种情况下带排转矩随主被动部分转速差的变化趋势是一致的,表面张力的作用使带排转矩增加。当接触角为30°时,其峰值转矩增加约1.97%;而当接触角为20°时,峰值转矩较无表面张力时增加约2.25%。所以,湿润接触角越小,带排转矩增加量越大,主要是因为越小的接触角会导致越大的接触面积,从而引起等效外径增大,进而使带排转矩增大。但是,从计算结果也能看出,带排转矩增大的幅值并不明显。

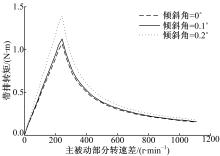
	Figure Option View Download New Window
	图5 表面张力对带排转矩的影响Fig.5 Influence of surface tension on drag torque

对于摩擦副不平行度的分析,分别选取对偶钢片的倾斜角度为0°、0.1°和0.2°进行计算,计算结果如图6所示。不难发现,随着对偶钢片倾斜角度的增加,离合器带排转矩增大,且倾斜角度越大,带排转矩增加越明显。当倾斜角度为0.1°时,峰值转矩较未倾斜时增大5.75%;当倾斜角度为0.2°时,峰值转矩较未倾斜时增大22.8%,增加的程度较大。这主要是因为随倾斜角度的增加,摩擦片与对偶钢片之间的接近程度越来越高,根据牛顿内摩擦定律,使得润滑油的切应力增大,从而引起带排转矩显著增大。

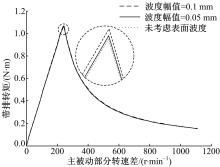
	Figure Option View Download New Window
	图6 摩擦副不平行度对带排转矩的影响Fig.6 Influence of nonparallelism of friction pair on drag torque

本文分析了表面波度对带排转矩的影响,分别选取波度幅值为0.05 mm和0.1 mm进行分析,所得结果如图7所示。当名义油膜厚度为0.6 mm、波度幅值为0.05 mm时,带排转矩峰值仅增加约0.037%;而当波度幅值为0.1 mm时,转矩峰值增加约1.48%。可见,表面波度对带排转矩的影响较小,

	Figure Option View Download New Window
	图7 表面波度对带排转矩的影响Fig.7 Influence of surface waviness on drag torque

在本文的计算条件下,仅波度幅值增加到与名义油膜厚度同等数量级时,才产生一定的影响。但是,这种影响也不能忽略,当摩擦副因过热等因素发生变形但仍不足以导致失效时,摩擦副在继续工作过程中表面波度的这种效用会被放大,离合器带排损失值将会明显增大。

为验证所建立的改进的湿式离合器带排转矩模型,专门搭建了湿式离合器带排转矩测试试验台,试验台实际布局和湿式离合器包箱内部结构如图8所示。试验中为了避免因润滑油温度变化而引起的黏度变化,试验前将润滑油温度预热到50 ℃,这样在短时间内油温不会发生变化,进而在该温度下完成试验,相应工况参数如下:润滑油密度 ρ=875 kg·m^-3,

	Figure Option View Download New Window
	图8 湿式离合器带排转矩试验台及被试件内部结构Fig.8 Test rig for testing drag torque of wet clutch and inner configuration of the tested component

润滑油黏度 μ=0.062 Pa·s,表面张力系数 σ=0.034 N·m^-1,摩擦片内径 R_i=86 mm,摩擦片外径 R_o=125 mm,表面波度幅值 h_n=80 μm,润滑油供应流量 Q_i=1.5 L·min^-1,名义油膜厚度 h₀=0.6 mm,摩擦副数 Z=4。将相关参数代入改进模型和原模型计算,并将计算结果与试验数据进行比较。

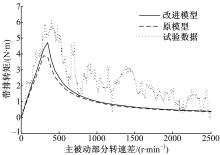
试验中离合器主动部分转速从0增加到2500 r/min,被动部分固定,所得试验结果与新模型及文献[9]中的模型对比如图9所示。在计算过程中,将可能的摩擦副倾斜全部等效到某一对偶钢片上,认为只有该对偶钢片发生倾斜,倾斜角度为0.15°。从图9可以看出,改进的模型与试验结果更加接近。但是同时能够发现,改进模型较试验结果依然偏小,而且在转速大于500 r/min时差异明显。这主要因为随着转速的增加,由于振动等随机因素使摩擦副实际间隙发生变化,不再保持名义值,从而造成测试的带排转矩值偏高。同时试验中不能完全排除离合器包箱中轴承等干扰因素的存在,这是引起测试值偏高的另一个可能原因。虽然存在一定差异,但改进模型与试验数据之间具有更好的趋势一致性和数值接近程度。

	Figure Option View Download New Window
	图9 模型结果与试验数据对比Fig.9 Contrast between model results and test data

4 结论

(1)基于润滑油的表面张力及固-液界面接触角,对离合器摩擦副间油膜径向压力分布进行了修正,进而对湿式离合器的带排转矩模型进行了改进,通过计算发现表面张力使湿式离合器带排转矩增加。

(2)分析了摩擦副不平行度对带排转矩的影响。研究发现,摩擦副不平行度使带排转矩增加,而且不平行程度越大,带排转矩损失增加越明显。

(3)分析了摩擦副表面波度对带排转矩的影响。研究发现,表面波度使带排转矩有所增大,但这种影响并不显著。只有当波度幅值与名义油膜厚度接近时,带排转矩的增加才会相对明显。

(4)通过与试验结果对比发现,改进的模型与试验结果更加接近。改进的模型较原模型能够更好地预测带排转矩。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Hashimoto H, Wada S, Murayama Y. The performance of a turbulent lubricated sliding bearing subject to centrifugal effect[J]. Transaction of Japanese Society of Mechanical Engineering, 1984, 49: 1753-1761. [本文引用:1]
[2]	Kato Y, Murasugi T, Hirano H, et al. Fuel economy improvement through tribological analysis of the wet clutches and brakes of an automatic transmission[J]. Society of Automotive Engineers of Japan, 1993, 16(12): 57-60. [本文引用:1]
[3]	Yuan Yi-qing, Eysion A Liu, James Hill, et al. An improved hydrodynamic model for open wet transmission clutches[J]. Journal of Fluid Engineering, 2007, 129: 333-337. [本文引用:2] [JCR: 0.886]
[4]	Yuan Yi-qing, Attibele P. CFD simulation of the flows within disengaged wet clutches of an automatic transmission[J]. SAE Transaction, 2003, 56(3): 1760-1768. [本文引用:1]
[5]	Chinar R Aphale, Jinhyun Cho, William W Schultz, et al. Modeling and parametric study of torque in open clutch plates[J]. Journal of Tribology, 2006, 128: 422-430. [本文引用:1] [JCR: 1.213]
[6]	Chinar R Aphal. Drag reduction at low and high reynolds numbers[D]. Ann Arbor: The University of Michigan, 2007. [本文引用:1]
[7]	Hu Ji-bin, Peng Zeng-xiong. Drag torque prediction model for the wet clutches[J]. Chinese Journal of Mechanical Engineering, 2009, 22(2): 238-243. [本文引用:1] [CJCR: 1.505]
[8]	张志刚, 周晓军, 李永军, 等. 湿式多片换挡离合器带排转矩的预测模型[J]. 浙江大学学报: 工学版, 2011, 45(4): 708-713. Zhang Zhi-gang, Zhou Xiao-jun, Li Yong-jun, et al. Drag torque prediction model of wet multi-disk shifting clutch[J]. Journal of Zhejiang University(Engineering Science), 2011, 45(4): 708-713. [本文引用:1] [CJCR: 0.551]
[9]	景琦. 湿式换挡离合器带排损失特性研究[D]. 北京: 北京理工大学机械与车辆学院, 2012. Jing Qi. Study on the drag loss characteristic of wet shift clutch[D]. Beijing: School of Mechanical Engineering, Beijing Institute of Technology, 2012. [本文引用:1]
[10]	Paul D W, None Z. Simulation of drag torque affecting synchronizers in a dual clutch transmission[J]. Springer, 2011, 28(5): 121-140. [本文引用:1]
[11]	刘佐民. 摩擦学理论与设计[M]. 武汉: 武汉理工大学出版社, 2009: 8-13. [本文引用:2]
[12]	张也影. 流体力学[M]. 2版. 北京: 高等教育出版社, 1998: 36-39. [本文引用:1]
[13]	杨惠霞, 顾永泉. 考虑表面锥度、波度和粗糙度的两维机械密封混合摩擦研究[J]. 流体机械, 1994, 22(5): 3-10. Yang Hui-xia, Gu Yong-quan. Study on two dimensional mixed friction of mechanical face seals considering surface taper, waviness and roughness[J]. Fluid Machinery, 1994, 22(5): 3-10. [本文引用:1] [CJCR: 0.3966]

1984

0.0

... 理论建模的主要思路是通过分析离心力作用下的层流或紊流状态本构方程,建立摩擦副间油膜压力分布方程及带排转矩模型^[1,2,3] ...

1993

0.0

... 理论建模的主要思路是通过分析离心力作用下的层流或紊流状态本构方程,建立摩擦副间油膜压力分布方程及带排转矩模型^[1,2,3] ...

2007

0.886

0.0

J. Fluids Eng.. 2007, 129(3):333-337

An Improved Hydrodynamic Model for Open Wet Transmission Clutches

Yiqing Yuan Eysion A. Liu, James Hill Qian Zou

DaimlerChrysler Corporation, 800 Chrysler Dr., Auburn Hills, MI 48326 DaimlerChrysler Corporation, 800 Chrysler Dr., Auburn Hills, MI 48326 Oakland University, Rochester, MI

A mathematical model describing the hydrodynamics of the flow within a disengaged wet transmission clutch is presented. The primary improvement of this model over the existing ones is the inclusion of the surface tension effect, which is expressed in the pressure equation as an additional term. The drag torque predicted by the model correlates well with the test data for nongrooved clutch packs. The significance of the surface tension in this type of flows is discussed as well.

... 理论建模的主要思路是通过分析离心力作用下的层流或紊流状态本构方程,建立摩擦副间油膜压力分布方程及带排转矩模型^[1,2,3] ...

... 在等效外径外侧(与空气接触一侧),由于液体表面张力的存在,油膜表面会产生压力波动^[3,10] ...

2003

0.0

... 同时,基于计算流体动力学(CFD)仿真分析表面沟槽对湿式多片式离合器带排转矩的影响^[4,5,6] ...

2006

1.213

0.0

J. Tribol.. 2006, 128(2):422-430

Modeling and Parametric Study of Torque in Open Clutch Plates

Chinar R. Aphale Jinhyun Cho William W. Schultz Steven L. Ceccio Takao Yoshioka Henry Hiraki

Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI 48105 caphale@umich.edu Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI 48105 jinhyunc@umich.edu Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI 48105 schultz@umich.edu Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI 48105 ceccio@umich.edu Dynax Corporation, Hokkaido, Japan yoshioka-t@mail.dxj.co.jp Dynax Corporation, Hokkaido, Japan hiraki-h@mail.dxj.co.jp

The relative motion of the friction and separator plates in wet clutches during the disengaged mode causes viscous shear stresses in the fluid passing through the 100 microns gap. This results in a drag torque on both the disks that wastes energy and decreases fuel economy. The objective of the study is to develop an accurate mathematical model for the above problem with verification using FLUENT and experiments. Initially we two consider flat disks. The mathematical model calculates the drag torque on the disks and the 2D axisymmetric solver verifies the solution. The surface pressure distribution on the plates is also verified. Then, 3D models of one grooved and one flat disk are tested using CFD, experiments and an approximate 3D mathematical model. The number of grooves, depth of groove and clearance between the disks are studied to understand their effect on the torque. The study determines the pressure field that eventually affects aeration incipience (not studied here). The results of the model, computations and experiments corroborate well in the single-phase regime.

... 同时,基于计算流体动力学(CFD)仿真分析表面沟槽对湿式多片式离合器带排转矩的影响^[4,5,6] ...

2007

0.0

... 同时,基于计算流体动力学(CFD)仿真分析表面沟槽对湿式多片式离合器带排转矩的影响^[4,5,6] ...

2009

0.0

1.505

... 国内的研究方法与国外类似,主要基于黏性流体力学的层流理论及牛顿内摩擦定律建立带排转矩的预测模型,并进行相应的试验验证^[7,8,9] ...

2011

0.0

0.551

... 国内的研究方法与国外类似,主要基于黏性流体力学的层流理论及牛顿内摩擦定律建立带排转矩的预测模型,并进行相应的试验验证^[7,8,9] ...

2012

0.0

... 国内的研究方法与国外类似,主要基于黏性流体力学的层流理论及牛顿内摩擦定律建立带排转矩的预测模型,并进行相应的试验验证^[7,8,9] ...

2011

0.0

... 在等效外径外侧(与空气接触一侧),由于液体表面张力的存在,油膜表面会产生压力波动^[3,10] ...

2009

0.0

... 同时由于固-液界面的自由能,为保证润滑油与空气接触部分表面积最小,摩擦副与润滑油的固-液界面的接触角变小,浸润面积增大^[11,12],综合作用下的结果如图2所示,这些因素的作用对等效外径的大小产生影响 ...

... m^[11],一般情况下也在几十微米到100 #cod#x003bc ...

1998

0.0

1994

0.0

0.3966

... 一般表面波度的表征形式为^[13]: ...