基于移动瓶颈交通波理论的上坡路段货车对客车干扰建模

引用本文

陈永恒, 王新慧, 曲昭伟, 尉明丽, 张虎. 基于移动瓶颈交通波理论的上坡路段货车对客车干扰建模. 吉林大学学报: 工学版, 2014, 44(5): 1290-1295[CHEN Yong-heng, WANG Xin-hui, QU Zhao-wei, WEI Ming-li, ZHANG Hu. Modeling of buses interference with trucks based on kinematic wave theory of moving bottlenecks. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1290-1295] 复制到剪切板

Permissions

基于移动瓶颈交通波理论的上坡路段货车对客车干扰建模

陈永恒, 王新慧, 曲昭伟, 尉明丽, 张虎

吉林大学交通学院, 长春 130022

通信作者:曲昭伟（1962-）,男,教授,博士生导师.研究方向:交通流理论,交通视频处理,交通控制. E-mail:quzw@jlu.edu.cn

作者简介:陈永恒（1978-）,男,副教授,博士.研究方向:交通控制与交通组织.E-mail:cyh@jlu.edu.cn

基金:国家自然科学基金项目（51278220）

摘要

对单行双车道上坡路段、多种车型的复杂条件下货车产生移动瓶颈的干扰机理进行了研究,以多种货车叠加干扰的情况作为干扰建模的基本环境,通过车道通行能力折减来反映干扰大小,建立了干扰模型。利用模型分析了货车车道限制对车道通行能力的影响,结果表明:对高速公路采取货车车道限制能够提升车道的平均通行能力。

关键词: 交通运输系统工程; 货车对客车干扰模型; 移动瓶颈交通波理论; 车道限制

中图分类号:U461 文献标志码:A 文章编号:1671-5497(2014)05-1290-06

Modeling of buses interference with trucks based on kinematic wave theory of moving bottlenecks

CHEN Yong-heng, WANG Xin-hui, QU Zhao-wei, WEI Ming-li, ZHANG Hu

College of Transportation, Jilin University, Changchun 130022,China

Abstract

The mechanism of buses interference with trucks is studied under complicated conditions, including two-lane upslope one-way road and multiple types of vehicles. An interference model is proposed for the capacity reduction of freeway bottlenecks caused by trucks. The model is applied to estimate the impact of truck lane restriction on the passing capacity. It is found that the system capacity is maximized when all the trucks share one lane. Truck lane restriction can effectively enhance the passing capacity of freeway.

Keyword: engineering of communications and transportation system; the modeling of cars interference with trucks kinematic; wave theory of moving bottlenecks; lane restrictions

Show Figures

0 引言

近年来高速公路中载重货车的比例不断增长,车道上客货车混行现象较为突出,而货车自身的加减速特性较差,尤其是在上坡路段,速度下降较大,而坡度对小客车的加速干扰较小,从而客货车之间的速度差拉大,货车对小客车的影响加剧。随着交通量的增加,车辆自由行驶空间不足,货车干扰强度急剧增长,货车后续车辆产生排队。Newell^{[ 1]}针对这种排队现象,建立了移动瓶颈交通波模型;Laval等^{[ 2, 3, 4, 5]}利用概率微观模型获得了单货车引发移动瓶颈的路段通行能力模型,他先后利用移动瓶颈理论分析了货车产生瓶颈时对车道通行能力的干扰情况,以及多车道多货车车型对通行能力的干扰。以上模型对货车产生的瓶颈机理进行了分析,并建立了相应的干扰模型,而Laral、Daganzo等^{[ 5]}的研究忽略了车型变化对干扰程度的影响;Laval分析了货车车型对车道通行能力的干扰,但没有考虑每种慢车产生的波速的差异。在国内,高学辉、刘晨辉等^{[ 6, 7, 8, 9]}分析了货车在车道上起到的干扰作用,并利用仿真软件对干扰程度进行了分析,但对货车引发瓶颈的作用机理分析不够深入。

本文针对高速公路车型多样化的特点,分析了货车在坡道上的到达关系对消散波波速传播的影响,建立了多种货车叠加干扰的干扰模型,并利用干扰模型分析了货车车道限制的作用。

1 货车干扰机理

货车在道路运行当中充当了一种障碍物的角色,相当于移动的瓶颈,对上游车辆产生干扰,进而产生排队,这种现象被称为移动瓶颈,结合交通三参数建立适合移动瓶颈的交通流理论称为移动瓶颈交通波(Kinematic wave theory of moving bottlenecks)模型。

1.1 货车产生移动瓶颈分析

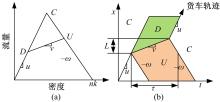
公路上的移动瓶颈制造者通常是由于速度差引起,而这种瓶颈通常产生在坡路上、出入口匝道处,或基本路段短时间内没有超车间隙处。假设车道流量、密度符合三角形关系,干扰路段为上坡路段,如图1(a)所示,当货车驶入坡道,货车干扰开始,车道通行能力下降直至货车驶离坡道,此时产生消散波 $\begin{matrix} ω \end{matrix}$ ,货车干扰路段长为 $\begin{matrix} L \end{matrix}$ ,干扰期间车道通行能力为 $\begin{matrix} U \end{matrix}$ (无干扰时车道通行能力为 $\begin{matrix} C \end{matrix}$ );图1(b)为货车的行驶轨迹,货车初始速度为自由流速度 $\begin{matrix} u \end{matrix}$ ,干扰路段车速为 $\begin{matrix} v \end{matrix}$ ,根据图形的关系可计算出干扰的时间以及不同状态下的流量、密度^{[ 6]}。

	Figure Option View Download New Window
	图1 移动瓶颈交通波流量-密度三角形关系以及货车轨迹Fig.1 Representation of a moving bottlenecks in a triangular fundamental diagram(flow-density);approximate truck trajectories and induced traffic states

1.2 货车干扰模型

单向一条车道、多种货车条件,假设货车的爬坡速度符合离散分布,表示为 G( v_i) = $\begin{matrix} \overset{i}{\sum_{j = 1}} \end{matrix}$ p_j,i=1,…,n,其中 $\begin{matrix} p_{j} \end{matrix}$ 为速度为 $\begin{matrix} v_{i} \end{matrix}$ 的货车流量占总货车流量的比例,且货车的速度满足 $\begin{matrix} v_{i} < v_{i + 1} 。 \end{matrix}$ 单车道货车到达关系假定为图2所示的关系,坡道上货车1对货车2产生干扰,尾随排队行驶,货车2对货车3产生干扰,排队继续,依次循环。根据移动交通波理论,相对干扰时间为 $\begin{matrix} {\tilde{τ}}_{i} = τ_{i} / τ (u), \end{matrix}$ 表达式如下:

$\begin{matrix} \frac{1}{{\tilde{τ}}_{i}} = \frac{v_{i} (u + w)}{u (w + v_{i})} (1) \end{matrix}$

式中: $\begin{matrix} {\tilde{τ}}_{i} \end{matrix}$ 为货车 $\begin{matrix} i \end{matrix}$ 产生的相对干扰时间; $\begin{matrix} τ_{i} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 种货车产生的干扰时间; $\begin{matrix} u \end{matrix}$ 为小客车的自由行驶速度; $\begin{matrix} w \end{matrix}$ 为波速。

	Figure Option View Download New Window
	图2 两种货车到达轨迹图例Fig.2 Example of a realization in a single lane and two types of trucks

货车到达坡底的流量包括两种: $\begin{matrix} U \end{matrix}$ 或 $\begin{matrix} C, \end{matrix}$ 那么到达的货车车辆数可表示为:

$\begin{matrix} m_{τ} (h) = \{\begin{matrix} λ_{i} h, h \leq τ \\ λ_{i} τ + (h - τ) λ_{i}^{*}, h > τ \end{matrix} (2) \end{matrix}$

式中: $\begin{matrix} λ_{i} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 种货车到达率; $\begin{matrix} h \end{matrix}$ 为货车车头时距; $\begin{matrix} λ_{i}^{*} \end{matrix}$ 为第 $\begin{matrix} i - 1 \end{matrix}$ 种货车到达率。

假定货车到达符合泊松分布,其车头时距符合以下分布:

$\begin{matrix} f_{H} (h_{i}) = \{\begin{matrix} λ_{i} e^{- h λ_{i}}, h_{i} \leq τ \\ e^{τ (λ_{i}^{*} - λ_{i})} λ_{i}^{*} e^{- h λ_{i}^{*}}, h_{i} > τ \end{matrix} (3) \end{matrix}$

平均车头时距 $\begin{matrix} {\bar{H}}_{i} \end{matrix}$ 为:

$\begin{matrix} {\bar{H}}_{i} = (1 - e^{- λ_{i} τ_{i}}) / τ_{i} + e^{- λ_{i} τ_{i}} / λ_{i}^{*} (4) \end{matrix}$

设货车占流量占总流量的百分比为 $\begin{matrix} p_{i}, 那么货车 i \end{matrix}$ 的到达率可表示为 $\begin{matrix} r, λ_{i} 、 λ_{i}^{*} \end{matrix}$ 可分别表示为 $\begin{matrix} λ_{i} = r p_{i} U_{i}; λ_{i}^{*} = r p_{i} U_{i + 1}^{*}, \end{matrix}$ 此时的流量为 $\begin{matrix} U_{i}^{*} = 1 / (r p_{1} {\bar{H}}_{i}), \end{matrix}$ 那么 $\begin{matrix} U_{n + 1}^{*} = C, \end{matrix}$ 由此推导出:

$\begin{matrix} \begin{matrix} λ_{i}^{*} = p_{i} / (p_{i + 1} {\bar{H}}_{i + 1}) (5) \\ λ_{i} τ_{i} = p_{i} φ (6) \end{matrix} \end{matrix}$

设 $\begin{matrix} {\bar{H}}_{i} = a_{i} + b_{i} {\bar{H}}_{i + 1}, \end{matrix}$ 参数 $\begin{matrix} a_{i} 、 b_{i} \end{matrix}$ 分别表示为 $\begin{matrix} a_{i} = (1 - e^{- p_{i} φ}) / λ_{i}, b_{i} = e^{- p_{i} φ} p_{i + 1} / p_{i}, \end{matrix}$ 则 $\begin{matrix} {\bar{H}}_{1} \end{matrix}$ = $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ a_i $\begin{matrix} \overset{i}{\prod_{j = 1}} \end{matrix}$ b_j。那么单车道多种货车的车道标准化通行能力可表示为:

$\begin{matrix} ρ = 1 / (r p_{1} {\bar{H}}_{1} C) (7) \end{matrix}$

将参数代入式(7),得到标准化通行能力:

$\begin{matrix} \frac{1}{ρ} = e^{- φ} - \overset{}{\sum_{}} {\tilde{τ}}_{i} (e^{- φG (v_{i})} - e^{- φG (v_{i - 1})}) (8) \end{matrix}$

2 适应单向两车道多种货车的干扰模型

单车道上的车流的行驶受到货车的干扰,无法自由行驶,货车成为瓶颈障碍物,后续车辆根据货车的车速进行排队行驶,而实际道路至少为两车道,车辆可在有可插间隙时进行换道,或允许时完成超车,在换道时产生货车并行的现象,两条车道同时产生干扰,也就是说可以用单车道货车干扰模型分析两车道同时干扰的情况。

2 .1 模型建立

(1)货车超车影响:两车道同时产生干扰情况包括两种,一种为货车在同一时间到达坡底同时对各自车道车辆产生干扰;另一种为除了货车1的其他货车换道,此时两种货车并行,对后续车辆产生干扰。

(2)客车超车影响:仅有客车超车则对两条车道上行驶的车流不存在影响,两车道相当于独立的两条车道,分别考虑两条车道各自的干扰情况,即为车道同时产生干扰的情况。

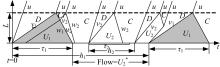
假设干扰路段为上坡路段,且坡长为 $\begin{matrix} L \end{matrix}$ ,货车在干扰路段两端的行驶速度均为自由流,爬坡车速低于自由流速度。驶入坡底,干扰产生,当货车行驶到干扰路段终点时,干扰源消失,产生消散波。假设货车到达为离散分布,到达符合泊松分布。

货车变为自由流时,产生消散波,且波速为:

$\begin{matrix} w = \frac{q_{1} - q_{2}}{k_{1} - k_{2}} (9) \end{matrix}$

式中: $\begin{matrix} k \end{matrix}$ 为车道密度; $\begin{matrix} q \end{matrix}$ 为流量,而 $\begin{matrix} q = kv, k = 1 / h_{l}, \end{matrix}$ 则货车产生的波速可表示为:

$\begin{matrix} w_{i} = \frac{k_{c} u - k_{i} v_{i}}{k_{c} - k_{i}} = \frac{u h_{li} - v_{i} h_{lc}}{h_{li} - h_{lc}} (10) \end{matrix}$

式中: $\begin{matrix} w_{i} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 种货车产生的波速; $\begin{matrix} h_{li} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 种货车为瓶颈时,排队车辆的平均车头间距; $\begin{matrix} h_{lc} \end{matrix}$ 为无瓶颈时车辆的平均车头间距。

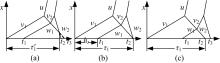
每种货车产生的干扰时间均与自身的爬坡速度、波速及干扰路段长度有关,假设干扰路段一定,分析两类货车在路段上的到达关系,如图3所示,货车1产生的干扰时间与两车到达车头时距有关。图3( b)为两种货车波速恰好在坡底相交,此时为两种状态的分界点,下面推导两车到达关系干扰状态公式。

	Figure Option View Download New Window
	图3 两种波速传播关系Fig.3 Relationship of waves by two kinds of trucks

如图3( b)( c),货车1单独干扰时间 $\begin{matrix} τ_{i} \end{matrix}$ 为:

$\begin{matrix} τ_{i} = \frac{L (v_{i} + w_{i})}{v_{i} w_{i}} (11) \end{matrix}$

当货车1与货车2之间的车头时距为图3( b)所示时,两个波恰好同时消失,而图3( a)为货车2产生的波追上了货车1产生的波,以波速2进行释放,则两者车头时距的临界值可表示为:

$\begin{matrix} {\tilde{h}}_{ti} = τ [1 - \frac{w_{i} (v_{i + 1} + w_{i + 1})}{w_{i + 1} (v_{i + 1} + w_{i})}] (12) \end{matrix}$

货车1的干扰时间变为:

$\begin{matrix} \begin{matrix} τ'_{1} = \frac{L}{v_{1}} + {\tilde{h}}_{t} (\frac{1}{v_{1} w_{1}} - \frac{1}{w_{1}^{2}}) + \\ {\tilde{h}}_{t} (\frac{\frac{1}{v_{2}} - \frac{1}{w_{2}}}{(1 - \frac{1}{v_{1} w_{2}}) (1 + \frac{1}{v_{1} w_{1}})}) (13) \end{matrix} \end{matrix}$

根据两种货车的到达车头时距关系,计算干扰时间:

$\begin{matrix} τ (v_{i}) = \{\begin{matrix} τ_{i}, h_{t} \geq {\tilde{h}}_{ti} \\ τ'_{i}, h_{t} < {\tilde{h}}_{ti} \end{matrix} (14) \end{matrix}$

式中: $\begin{matrix} {\tilde{h}}_{ti} \end{matrix}$ 为前、后两辆货车之间的车头时距。

每种货车产生的无量纲干扰时间可表示为:

$\begin{matrix} {\tilde{τ}}_{i} = τ (v_{i}) / τ (u) (15) \end{matrix}$

考虑单向两条车道上多种货车车道干扰情况。货车的速度为离散分布,且每种速度的货车在车道 $\begin{matrix} i \end{matrix}$ 上的速度分布满足:

$\begin{matrix} \begin{matrix} G (v_{1, i}) = \overset{i}{\sum_{j = 1}} p_{1, j} (16) \\ G (v_{2, i}) = \overset{i}{\sum_{j = 1}} p_{2, j} (17) \end{matrix} \end{matrix}$

式中: $\begin{matrix} G (v_{1, i}) 、 G (v_{2, i}) \end{matrix}$ 分别为第 $\begin{matrix} i \end{matrix}$ 种货车在车道1和车道2上的速度分布。

每种货车在车道 $\begin{matrix} l \end{matrix}$ 上的比例表示为:

$\begin{matrix} \begin{matrix} p_{1, i} = \frac{p_{i} ξ_{i}}{\overset{n}{\sum_{i = 1}} p_{i} ξ_{i}} (18) \\ p_{2, i} = \frac{p_{i} (1 - ξ_{i})}{\overset{n}{\sum_{i = 1}} p_{i} (1 - ξ_{i})} (19) \end{matrix} \end{matrix}$

式中: $\begin{matrix} p_{i} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 种货车占货车流量的比例; $\begin{matrix} ξ_{i} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 种货车在车道1上的比例。

车道 $\begin{matrix} l \end{matrix}$ 上总货车占总流量的比例由以上公式推导出,表达式为:

$\begin{matrix} \begin{matrix} r_{1} = r \overset{n}{\sum_{i = 1}} p_{i} ξ_{i} (20) \\ r_{2} = r \overset{n}{\sum_{i = 2}} p_{i} (1 - ξ_{i}) (21) \end{matrix} \end{matrix}$

式中: $\begin{matrix} r \end{matrix}$ 为货车占总流量比例。

令 $\begin{matrix} φ_{l} = r_{l} k L 。 \end{matrix}$ 由以上变量可推导出车道标准化通行能力表达式如下:

$\begin{matrix} \begin{matrix} \frac{1}{ρ_{1}} = \exp (- φ \overset{n}{\sum_{i = 1}} p_{i} ξ_{i}) - \\ \overset{n}{\sum_{i = 1}} {\tilde{τ}}_{i} [\exp (- φ \overset{i}{\sum_{j = 1}} p_{i} ξ_{i}) - \\ \exp (- φ \overset{i}{\sum_{j = 1}} p_{j - 1} ξ_{i - 1})] φ (22) \\ \frac{1}{ρ_{2}} = \exp [- φ \overset{n}{\sum_{i = 2}} p_{i} (1 - ξ_{i})] - \\ \overset{n}{\sum_{i = 2}} {\tilde{τ}}_{i} {\exp [- φ \overset{i}{\sum_{j = 2}} p_{j} (1 - ξ_{j})] - \\ \exp [- φ \overset{i}{\sum_{j}} p_{j - 1} (1 - ξ_{j - 1})]} (23) \end{matrix} \end{matrix}$

式中: $\begin{matrix} ρ_{l} 、 ρ_{2} \end{matrix}$ 分别为车道1和车道2的标准化通行能力。

$\begin{matrix} ρ_{1} 、 ρ_{2} \end{matrix}$ 分别描述了各自车道上通行能力的变化趋势,那么这个车道的通行能力变化则以两条车道的平均值来描述:

$\begin{matrix} ρ = \frac{1}{2} (ρ_{1} + ρ_{2}) (24) \end{matrix}$

2 .2 模型验证

由推导可知 $\begin{matrix} \frac{1}{{\tilde{τ}}_{i}} = \frac{U_{i}}{C}, 当 φ \to \infty \end{matrix}$ 时,即干扰无限大时, $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ p_iξ_i→ ¥, exp( -φ $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ p_iξ_i) =0;而 $\begin{matrix} p = 0 \end{matrix}$ 时,即 $\begin{matrix} G (v_{l, o}) = 0, \end{matrix}$ 那么可推出 $\begin{matrix} ρ_{1} = 1 / {\tilde{τ}}_{1}, ρ_{2} = 1 / {\tilde{τ}}_{2} 。 \end{matrix}$

$\begin{matrix} {\tilde{τ}}_{i} \end{matrix}$ 与自由流速度、波速、货车 $\begin{matrix} i \end{matrix}$ 爬坡速度密切相关,体现了不同状态车流之间产生的干扰,进而产生波,致使车道通行能力产生损失。

3 货车干扰趋势分析

利用 MATLAB软件对各种条件下的车道通行能力模型进行分析, 得到图4、图5所示结果。

	Figure Option View Download New Window
	图4 通行能力 ρ随各货车在车道1上比例的变化趋势Fig.4 Trend of capacity ρ with the proportion trucks on lane1

	Figure Option View Download New Window
	图5 平均通行能力 ρ随 φ的变化趋势Fig.5 Trend of average capacity ρ with the φ

以两种货车为分析对象,通过对某实际货车运行速度的调查,爬坡速度分别取50、70 km/h,自由流速度为120 km/h,上坡时产生的波速分别为10、13 m/s,根据干扰时间公式计算可得出两种车型无量纲干扰时间分别为0 .68、0 .84 s。

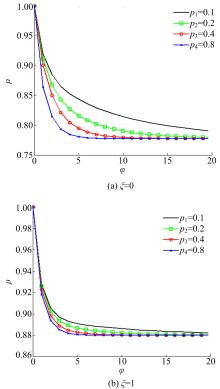
图4中,u =120 km/h,k =124 pcu/km/Ln,L =1 km,当每种货车的相对比例不变时,随着总货车比例的不断升高,通行能力不断下降,而当货车比例增长到一定程度时,其对道路通行能力的影响也趋于平稳;当总货车流量不变时,随着货车1的比例不断升高,车道1的通行能力一直降低,且降低幅度较大,而车道2的通行能力随着慢速车型数量的减少,通行能力恢复到理想通行能力。

车道1上的固定车型为货车1,即车道1为混行车道,通过每一列图形的对比,车道1的通行能力随货车比例的增加而降低,通过每行图形对比可知,车道1上货车1达到一定值时,车道的通行能力基本不变。

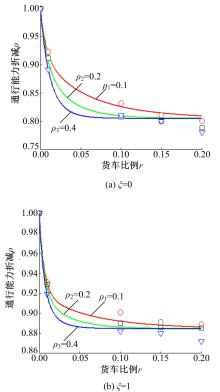
由图5可知: $\begin{matrix} ξ = 1 \end{matrix}$ 时,车道的平均通行能力达到最大值,即车道2为客车专用车道,车道为混行车道; $\begin{matrix} ξ = 0 \end{matrix}$ 时,车道1、2均为混行车道,此时的干扰较大,从而证明了车道限制能够提升道路的平均通行能力。

4 仿真验证

车道通行能力受货车干扰产生一定损失,但是由于实际数据无法获得,因此,本文利用 VISSIM仿真技术对模型进行验证^{[ 10]}。主要通过对不同货车比例下车道的通行能力进行仿真,验证本文所建模型的可信度。

从图6中可知,当货车比例较小时,仿真结果能够很好地与模型计算结果吻合,但随着货车比例的增长,仿真输出的结果与模型计算结果产生偏差。由于本文的假设为货车到达符合泊松分布,当货车比例不断增加时,很难让货车的到达符合泊松分布,因此,本模型的适用范围为货车比例较小时,即货车比例在0 ~20 %之间均有较好的拟合度。

	Figure Option View Download New Window
	图6 仿真验证Fig.6 Agreement between simulation of the exact process and capacity formulae

5 结束语

以高速公路上坡路段多种货车到达关系为研究的出发点,分析了多种货车产生消散波的传播关系,以移动交通波理论为理论基础,建立了多种货车叠加干扰模型,以通行能力折减来反映干扰程度。通过研究货车占总流量的比例和各种货车占总货车流量的比例来分析两条车道的通行能力折减趋势。货车对客车行驶存在干扰,且干扰大小随着货车比例的增加而增大,多种货车与单一货车干扰不同,当采取货车车道限制时,车道平均通行能力最高。通过对两车道多种货车车型进行仿真,得到不同货车比例条件下的车道通行能力,分析了货车对车道通行能力的折减大小与本文所建模型之间的吻合度,并以此验证此模型的适用范围。货车比例小于20 %时,仿真结果与模型计算结果较为吻合。

本文的货车干扰模型中主要考虑货车比例较小时,即货车分布符合泊松分布时进行的理论建模,而当货车比例增大时此模型与实际运行情况存在偏差。模型适用范围是货车比例为0 ~20 %。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Newell G F. A moving bottleneck[J]. Transportation Research Board, 1998, 32(8): 531-537 [本文引用:1]
[2]	Laval Jorge A. Stochastic processes of moving bottlenecks[C]∥Transportation Research Board of the National Academies, Washington DC, 2006 [本文引用:1]
[3]	Laval Jorge A. Effects of geometric design on freeway capacity: impacts of truck lane restrictions[J]. Transportation Research Part B, 2009, 43(6): 720-728 [本文引用:1] [JCR: 2.944]
[4]	Laval Jorge A. Hybrid models of traffic flow: impacts of bounded vehicle accelerations[D]. Berkeley: University of California, 2004 [本文引用:1]
[5]	Laval J A, Daganzo C F. Lane-changing in traffic streams[J]. Transportation Research Part B, 2006, 40(3): 251-264 [本文引用:2] [JCR: 2.944]
[6]	刘晨辉. 基于货车交通影响的高速公路车道限制研究[D]山东: 山东大学土建与水利学院, 2012 Liu Chen-hui. Freeway lane restrichine research based on truck traffic impact[D]. Shand ong: School of Civil Engineering, Shand ong University. [本文引用:2]
[7]	林航飞, 付强, 张红军. 基于移动瓶颈理论的高速公路货车影响对策[J]同济大学学报: 自然科学版, 2007, 35(9): 1209-1213 Lin Hang-fei, Fu Qiang, Zhang Hong-jun. Moving bottleneck theory-based new countermeasure for influence heavy vehicles[J]. Journal of Tongji University(Natural Science), 2007, 35(9): 1209-1213 [本文引用:1] [CJCR: 0.634]
[8]	高学辉, 王刚, 刘艳忠, 等. 基于移动瓶颈理论的高速公路重载货车影响效应研究[J]山东科技大学学报: 自然科学版, 2010, 29(3): 100-104 Gao Xue-hui, Wang Gang, Liu Yan-zhong, et al. Study on the effect of full-load lorry on freeway based on moving bottleneck thery[J]. Journal of Shongdong University of Science and Technology, 2010, 29(3): 100-104 [本文引用:1]
[9]	曲昭伟, 王殿海, 姚荣涵. 信号交叉口起动波的运动学模型[J]吉林大学学报: 工学版, 2008, 38(2): 268-272 Qu Zhao-wei, Wang Dian-hai, Yao Rong-han. Kinematic model of start wave at signalized intersection[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(2): 268-272 [本文引用:1] [CJCR: 0.701]
[10]	Hossam Abdelgawad, Baher Abdulhai. Simulation of exclusive truck facilities on urban freeways[J]. Journal of Transportation Engineering, 2011, 137(8): 547-562 [本文引用:1] [JCR: 0.863]

1998

0.0

. 1998, 32(8):null-null

A moving bottleneck

... Newell^[1]针对这种排队现象,建立了移动瓶颈交通波模型 ...

2006

0.0

... Laval等^[2,3,4,5]利用概率微观模型获得了单货车引发移动瓶颈的路段通行能力模型,他先后利用移动瓶颈理论分析了货车产生瓶颈时对车道通行能力的干扰情况,以及多车道多货车车型对通行能力的干扰 ...

2009

2.944

0.0

. 2009, 43(6):720-728 DOI:10.1016/j.trb.2009.01.003

Effects of geometric design on freeway capacity: impacts of truck lane restrictions

Abstract This paper presents a framework for estimating analytical expressions for the capacity reductions caused by a subset of vehicles forced to slow down at horizontal/vertical curves on multilane freeways. In each lane the underperforming stream is described in terms of its desired speed distribution (either discrete or continuous), and it is explicitly modeled as a stochastic process that disturbs light vehicles as per Newell’s kinematic wave theory of moving bottlenecks. The model is applied for estimating the impact of truck lane restrictions. It is found that system capacity is maximized either (i) when each truck type uses a different lane or (ii) when they share the same lane, depending on the relative proportion of heavy trucks. Moreover, this application sheds some light to the puzzling empirical result in several places around the world, where time and time again it is observed that the operational improvements of truck lane restrictions are small or negligible.

2004

0.0

2006

2.944

0.0

. 2006, 40(3):null-null

Lane-changing in traffic streams

... 以上模型对货车产生的瓶颈机理进行了分析,并建立了相应的干扰模型,而Laral、Daganzo等^[5]的研究忽略了车型变化对干扰程度的影响 ...

2012

0.0

... 在国内,高学辉、刘晨辉等^[6,7,8,9]分析了货车在车道上起到的干扰作用,并利用仿真软件对干扰程度进行了分析,但对货车引发瓶颈的作用机理分析不够深入 ...

... 图1(b)为货车的行驶轨迹,货车初始速度为自由流速度 u,干扰路段车速为 v,根据图形的关系可计算出干扰的时间以及不同状态下的流量、密度^[6] ...

2007

0.0

0.634

. 2007, 35(9):1209-1213

Moving bottleneck theory-based new countermeasure for influence heavy vehicles

在分析货运车辆造成的移动瓶颈影响规律基础上,根据移动瓶颈随时间、空间动态变化的特点,提出针对性解决策略:每隔一定距离增加一条车道,供车辆超车,以缓解移动瓶颈的影响.仿真验证表明,流量在每小时1 000辆左右时,与直接扩建成双向六车道高速公路相比,该策略以不到50%的投资可以达到超过70%的改善效果;并且此策略有较好的流量增长适应性和与后续策略的连续性,从而可减少投资浪费.

2010

0.0

2008

0.0

0.701

. 2008, 38(2):268-272

Kinematic model of start wave at signalized intersection

College of Transportation,Jilin University,Changchun 130022,China

Based on the kinematic characteristics of the vehicle start wave propagation,a kinematic model for the vehicle start wave which accords with the reality and whose parameters are explicit was built.The data acquisition scheme and the data processing method were designed.The model was calibrated by the survey data in Changchun city and the velocity of the vehicle start wave propagation was calculated by the model.The observed velocity of the vehicle start wave propagation was obtained from the survey data directly and the corresponding derived propagation characteristics of the vehicle start wave.The relative error between the two wave velocities obtained by the kinematic model and the direct observation is about 5%.The proposed model can provide a theoretical basis for the urban traffic signal control.

为寻求一种符合实际且参数意义明确的信号交叉口起动波模型，根据起动波传播的运动学特性建立了起动波的运动学模型。设计了数据采集方案和数据处理方法。利用长春市实际调查数据标定了模型，并得到了波速计算值。按照起动波传播特性，由实际调查数据计算了波速观测值。结果表明，运动学起动波模型的波速理论值与实际观测值的相对误差约为5%。该模型不依赖于传统交通波模型，参数意义明确，标定方法简单，波速计算值与观测值接近，为城市交通信号控制提供更可靠的理论依据。

2011

0.863

0.0

... 4 仿真验证车道通行能力受货车干扰产生一定损失,但是由于实际数据无法获得,因此,本文利用VISSIM仿真技术对模型进行验证^[10] ...