基于SVM灵敏度的城市交通事故严重程度影响因素分析

引用本文

孙轶轩, 邵春福, 岳昊, 朱亮. 基于SVM灵敏度的城市交通事故严重程度影响因素分析. 吉林大学学报: 工学版, 2014, 44(5): 1315-1320[SUN Yi-xuan, SHAO Chun-fu, YUE Hao, ZHU Liang. Urban traffic accident severity analysis based on sensitivity analysis of support vector machine. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1315-1320] 复制到剪切板

Permissions

基于SVM灵敏度的城市交通事故严重程度影响因素分析

孙轶轩¹, 邵春福¹, 岳昊¹, 朱亮²

1.北京交通大学城市交通复杂系统理论与技术教育部重点实验室, 北京 100044

2.中国铁道科学研究院运输及经济研究所, 北京 100081

通信作者:邵春福(1957-),男,教授.研究方向:交通安全.E-mail:cfshao@bjtu.edu.cn

作者简介:孙轶轩（1982-）,男,博士研究生.研究方向:交通安全.E-mail:squallsyx@163.com

基金:“973”国家重点基础研究发展计划项目（2012CB725403）; 国家自然科学基金国际合作重大项目（71210001）

摘要

基于某中小城市4881起交通事故现场数据,构建了基于“道路交通事故信息系统”事故数据的特征变量集;以一般事故、严重事故作为二分类标签,建立事故严重程度支持向量机(SVM)分类识别模型,并分别通过网格搜索法、遗传算法进行模型核参数寻优;最后,通过单因素局部灵敏度分析方法,研究各个特征变量对模型测试集分类精度的影响,进一步确定事故严重程度的核心影响因素。结果表明:SVM模型在训练集和测试集上的分类精度均在80%左右,表现出良好的分类识别效果和泛化能力;事故属性、车辆属性中有8个特征变量,显著影响SVM模型的分类精度。

关键词: 交通工程; 事故严重程度; 分类识别; 支持向量机; 智能算法

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2014)05-1315-06

Urban traffic accident severity analysis based on sensitivity analysis of support vector machine

SUN Yi-xuan¹, SHAO Chun-fu¹, YUE Hao¹, ZHU Liang²

1.MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing Jiaotong University, Beijing 100044, China

2.Transportation & Economic Research Institute, China Academy of Railway Sciences, Beijing 100081, China

Abstract

According to 4881 crash scene investigation data of accident database of a middle-size city, a Support Vector Machine (SVM) model is established for accident severity recognition, which is classified into low risk (property loss only) and high risk (injury or death involved). Grid Search (GS) and Genetic Algorithm (GA) are applied to find the best combination of penalty parameter C and Radial Basis Function (RBF) kernel parameter g. Then, the sensitivity analysis method is employed to evaluate the potential impacts of variables on the accident severity. The results show that the accuracies of the SVM model on both training and testing datasets are around 80%, which means better generalization performance: 8 variables of accident and vehicle attributes significantly influence the accident severity classification, which can be inferred as key factors.

Keyword: traffic engineering; traffic accident severity; classification recognition; support vector machine(SVM); intelligent algorithm

Show Figures

0 引言

目前,国内外已经在道路交通事故严重程度影响因素分析领域开展了广泛研究,其中以经典统计模型的相关应用最为广泛^{[ 1]},如二项或多项Logit、Probit模型^{[ 2, 3]},有序Logit、Probit或贝叶斯模型^{[ 4, 5]},嵌套Logit模型^{[ 6]},混合Logit模型^{[ 7]}等。国内学者李世民等^{[ 8]}利用累积Logit模型研究了交叉口交通事故严重程度与转弯车辆、用地性质等因素的关系;马壮林等^{[ 9, 10]}分别利用累积Logit模型和灰色模型研究了道路设计因素对隧道交通事故严重程度的影响;侯树展等^{[ 11]}利用主成分分析法研究了交通流特征和高速公路事故严重程度之间的联系。考虑到经典统计模型的缺陷和不足^{[ 12]},近年来有学者开始尝试将非参数、人工智能方法应用于交通事故严重程度影响因素分析,代表性的如分类回归树模型^{[ 13]},贝叶斯网络模型^{[ 14]},神经网络模型^{[ 15]}等。研究表明,非参数模型在实证研究中具有更优的统计拟合度和泛化能力^{[ 16, 17]}。

分析研究现状可知,在交通事故的空间分布上,现有研究多选择交通流特征稳定、道路环境相对简单的路段或区域,如高等级公路的路口或路段等作为研究对象,对发生于城市道路网中的交通事故研究相对较少;在严重程度影响因素的选择上,现有研究多选择因果关系较为明晰的交通流或道路设计等宏观指标,如交通流量、车型比例、车道宽度等,较少选择对事故信息采集数据进行直接分析,如碰撞形态、驾驶行为、涉事人员背景调查等。

综合考虑以上因素,本文以城市道路交通事故作为研究对象,提取“道路交通事故信息系统”中事故现场信息数据为候选影响因素指标,采用支持向量机(SVM)建立事故严重程度分类识别模型。但SVM方法长于处理小样本、非线性以及高维的分类识别问题,建模过程损失了特征变量对分类精度敏感程度的可解释性^{[ 1]},因此,本文通过计算各影响因素的单变量局部灵敏度,获得特征变量重要性排序^{[ 18]},并通过观察特征变量组合发掘城市道路交通事故严重程度规律,提出相应预防对策和控制措施。

1 SVM基本原理

1.1 SVM基本思想与核参数寻优

基于统计学习理论的结构风险最小化原则的SVM方法,基本思想是通过非线性变换将高维空间线性决策函数代替原样本属性空间非线性决策函数^{[ 19]},最终求解凸二次规划问题,保证解值的唯一性和全局最优性。该方法解决了神经网络方法难以避免的局部极值问题,算法复杂度与样本维度无关,最终能够在有限特征信息情况下充分发掘数据中隐含的规律。

SVM方法的核心是寻找线性可分情况下的最优分类面,对于线性可分训练样本集 T={( x₁, y₁),( x₂, y₂),…,( x_l, y_l)}∈( x×y) ^l,其中 x_i∈R ⁿ, y_i∈{ -1,1}, i=1,…, l,求解样本集最优化问题如式(1)所示:

$\begin{matrix} \{\begin{matrix} \min_{w, b} \frac{1}{2} ‖ w ‖^{2} \\ s . t . y_{i} ((w \cdot x_{i}) + b) \geq 1, i = 1, \dots, l \end{matrix} (1) \end{matrix}$

由最优解 w^*和 b^*确定的分类面,其决策函数为:

$\begin{matrix} \{\begin{matrix} (w^{*} \cdot x) + b^{*} = 0 \\ f (x) = sgn ((w^{*} \cdot x) + b^{*}) \end{matrix} (2) \end{matrix}$

当训练样本集线性不可分时,引入非负松弛变量 ξ_i≥0, $\begin{matrix} \overset{l}{\sum_{i = 1}} \end{matrix}$ ξ_i是错分样本度量值,同时引入惩罚参数 C作为综合权重,则原最优化问题变为:

$\begin{matrix} \{\begin{matrix} \min_{w, b} \frac{1}{2} ‖ w ‖^{2} + C \overset{l}{\sum_{i = 1}} ξ_{i} \\ s . t . y_{i} ((w \cdot x_{i}) + b) + ξ_{i} \geq 1, i = 1, \dots, l \end{matrix} (3) \end{matrix}$

通过满足 Mercer条件的核函数 K实现非线性变换,经过核函数映射后的决策函数为:

$\begin{matrix} f (x) = sgn (\overset{l}{\sum_{i = 1}} y_{i} α_{i}^{*} K (x_{i} \cdot x) + b^{*}) (4) \end{matrix}$

本文选用径向基( RBF)核函数:

$\begin{matrix} K (x, x_{i}) = \exp {- \frac{{|x - x_{i}|}^{2}}{g^{2}}} (5) \end{matrix}$

模型建立后,选用基于交叉验证法( CV)的综合分类精度来评价建模精度。常用交叉验证方法包括 HO-CV、 K-CV、 LOO-CV等。以 K-CV方法为例,将样本分割成 K个子样本,其中一个单独的子样本被留作测试集,其他 K-1个样本用作训练集。交叉验证重复 K次,每个子样本验证一次,平均 K次的结果或者使用其他结合方式,最终得到一个单一估测。此外,惩罚参数 C与 RBF核函数参数 g的选取很大程度上影响着 SVM模型的分类识别效果^{[ 20]}。许多研究者针对 SVM建模的参数寻优提出了各自的算法,常见算法有网格搜索法、双线性搜索法、梯度下降法、拟牛顿法、蒙特卡罗法、遗传算法等^{[ 21]},本文分别采用网格法和遗传算法对惩罚参数 C和 RBF核参数 g进行参数寻优,最终选取 K-CV条件下测试集精度最高和 C值最小的一组作为寻优结果。

1.2 基于SVM的灵敏度分析

灵敏度分析的目的在于确定模型各变量对输出结果影响的大小,通过灵敏度分析可知模型对哪些变量的变化敏感,从而确定各变量对模型结果的影响。具体分析方法主要包括局部灵敏度分析和全局灵敏度分析^{[ 22]}。

在复杂系统中,灵敏度指标(一阶灵敏度系数)常常无法直接计算得到。常用的简化计算方法是进行单因素局部灵敏度分析,即对某一变量进行微小变化,固定其他变量取值进行计算,也称为一次变化法,其灵敏度系数形式为:

$\begin{matrix} S_{i} = \frac{dv}{d p_{i}} (6) \end{matrix}$

式中: S_i为第 i个变量的灵敏度系数; v为模型输出结果,对SVM分类识别模型来说是测试集精度; p_i为第 i个变量。

对变量 p_i进行人工微小扰动,对连续型变量一般采用因子变化法,即将待分析变量增加或减少一个固定因子;或偏差变化法,即增加或减少量为标准偏差的倍数。对二值或多值分类变量计算灵敏度系数,则分别计算不同取值组合下的模型输出结果均值。单因素局部灵敏度分析法操作简单,当处理的变量变化幅度不大、变量间相互作用对模型输出结果影响不明显时,可以得到较为准确的灵敏度系数。城市道路交通事故严重程度影响因素特征变量多为二值或多值分类变量及少数连续变量^{[ 23]},适用于单因素局部灵敏度分析。

2 实证研究

2.1 数据集特征分析

如表1所示,本文选取某中小城市2006~2013年间事故数据作为实证研究对象,从数据库系统调取事故信息总计4881起,含财产损失事故2238起,致伤事故2224起,死亡事故419起。城市道路交通事故影响因素特征变量取自“事故基本信息”数据集,主要包括事故自身属性、致因属性、时空属性和行政属性等,其数据结构为事故现场信息代码^{[ 24]}。考虑到事故信息代码本身较为繁复,对其进行合并分类处理,使用“合成”变量对变量集进行初步降维,重点构造时间属性、事故自身属性、涉事驾驶员及车辆属性变量集。

表1 属性变量定义 Table 1 Attribute variables definition

2.2 SVM建模及参数寻优结果分析

利用Matlab平台Libsvm软件包进行实证数据的SVM建模及核参数寻优,并用序列最小化算法求解。考虑到死亡事故观测频数只有419起,本研究将事故严重程度分类标签定义为一般事故(2238起,占45.9%)和严重事故(2643起,占54.1%)两种分类,其中严重事故包含致伤(2224起)和死亡事故(419起)。

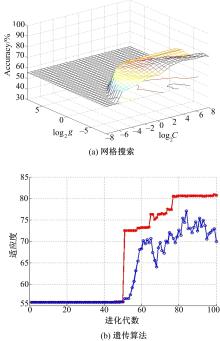
随机抽取一般事故和严重事故各500起作为测试集,剩余事故作为训练集,训练过程K-CV折数为5折。核参数寻优过程网格搜索法设定 C和 g选择范围为2^-8~2⁸,迭代步长为0.5;遗传算法设定进化代数为100,种群数量为20,模型核参数迭代过程如图1所示。

	Figure Option View Download New Window
	图1 训练集参数寻优视图Fig.1 C & g regression result of training dataset

经Matlab计算得出K-CV条件下的训练集精度、测试集精度及对应参数组合 C、 g值,如表2所示。

表2 参数寻优结果 Table 2 C & g regression result

参数寻优结果显示,网格搜索法和遗传算法在训练集精度和测试集精度上较为相近,均为80%左右,模型表现出良好的稳健性。其中网格搜索法标定的 C值较遗传算法小,因此 C=8, g=0 .01可确定为模型最优核参数组合。

2.3 灵敏度分析

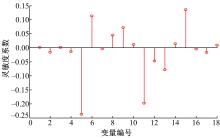
图2为实证数据集事故严重程度影响因素特征变量的单变量灵敏度系数。观察可知,18个变量中共有8个变量显著影响SVM模型的分类识别精度,具体包括事故类型为人车事故,单车事故,碰撞类型追尾、侧撞,气候与能见度,车辆信息中号牌是否合规,号牌种类是否为大型车辆,载运种类是否为载货车辆。8个变量中,灵敏度系数绝对值最大的前3个变量分别为事故类型为人车事故,气候与能见度不佳,涉事车辆载运种类为载货汽车。

	Figure Option View Download New Window
	图2 单变量局部灵敏度系数分布图Fig.2 Sensitive analysis of SVM variables regarding the classification accuracy

数据来源城市为小型重工业城市,核心经济产业涉及矿产资源开发利用、大型机械制造等重型工业及配套的仓储、物流运输业。多条高等级公路延伸或环绕城市建成区,承担部分城市路网功能。城市建成区人员流动密集,农村户籍人口比例大使得三轮车、助动车、农用车辆较多,本地和外地大型货运车辆比例较高,交通流结构复杂。观察灵敏度分析所确定的对SVM分类识别模型的精度影响最大的8个特征变量可以推断:大型载货汽车较容易发生致伤或致死的严重交通事故,这类事故既包含冲撞、碾压行人或非机动车的人车事故,也包括坠车、翻车、撞固定物等单车事故;较其他碰撞类型追尾和侧撞在严重交通事故中多发;不良的气候和能见度也易引起严重交通事故;车辆违法特征中,涉牌类违法车辆影响更为显著,应加强对该类违法行为的查处力度。

3 结束语

以某中小城市道路交通事故数据为样本,结合实际数据的可用性,构建了基于“道路交通事故信息系统”事故数据的特征变量集,并按照一般事故和严重事故二分类标签建立了基于SVM灵敏度分析的城市交通事故严重程度影响因素分析模型。灵敏度系数分析结果显示:时间属性、驾驶员属性对SVM分类识别精度影响不明显;事故属性、车辆属性中共有8个变量显著影响SVM分类识别的精度,可标记为事故严重程度的核心影响因素。核心影响因素中,SVM模型对车牌种类为大型货运车辆,事故类型为人车事故,气候与能见度条件为不佳3项特征变量最为敏感,该结论与实证数据集来源城市实际交通环境较为吻合,进而为实践层面对事故防治策略和措施的制定以及防治效果预测提供了理论支持。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Peter T, Savolainen P T, Fred L, et al. The statistical analysis of highway crash-injury severities: A review and assessment of methodological alternatives[J]. Accident Analysis and Prevention, 2011, 43(5): 1666-1676. [本文引用:2]
[2]	Chang H, Yeh T. Risk factors to driver fatalities in single-vehicle crashes: comparisons between non-motorcycle drivers and motorcyclists[J]. Journal of Transportation Engineering, 2006, 132(3): 227-236. [本文引用:1] [JCR: 0.863]
[3]	Malyshkina N, Mannering F. Empirical assessment of the impact of highway design exceptions on the frequency and severity of vehicle accidents[J]. Accident Analysis and Prevention, 2010, 42(1): 131-139. [本文引用:1]
[4]	Yamamoto T, Shankar V. Bivariate ordered-response probit model of driver's and passenger's injury severities in collisions with fixed objects[J]. Accident Analysis and Prevention, 2004, 36(5): 869-876. [本文引用:1]
[5]	Helai H, Chor C, Haque M. Severity of driver injury and vehicle damage in traffic crashes at intersections: a Bayesian hierarchical analysis[J]. Accident Analysis and Prevention, 2008, 40(1): 45-54. [本文引用:1]
[6]	Lee J, Mannering F. Impact of roadside features on the frequency and severity of run-off-roadway accidents: an empirical analysis[J]. Accident Analysis and Prevention, 2002, 34(2): 149-161. [本文引用:1]
[7]	Eluru N, Bhat C, Hensher D. A mixed generalized ordered response model for examining pedestrian and bicyclist injury severity level in traffic crashes[J]. Accident Analysis and Prevention, 2008, 40(3): 1033-1054. [本文引用:1]
[8]	李世民, 孙明玲, 关宏志. 基于累积Logistic模型的交通事故严重程度预测模型[J]. 交通标准化, 2009(3): 168-171. Li Shi-min, Sun Ming-ling, Guan Hong-zhi. Prediction model cumulative logistic for severity of road traffic accident[J]. Transport Stand ardization, 2009(3): 168-171. [本文引用:1]
[9]	马壮林, 邵春福, 李霞. 基于Logistic模型的公路隧道严重事故严重程度的影响因素[J]. 吉林大学学报: 工学版, 2010, 40(2): 423-426. Ma Zhuang-lin, Shao Chun-fu, Li Xia. Analysis of factors affecting accident severity in highway tunnels based on logistic model[J]. Journal of Jilin University(Engineering and Technology Edition), 2010, 40(2): 423-426. [本文引用:1] [CJCR: 0.701]
[10]	Ma Zhuang-lin, Shao Chun-fu, Ma She-qiang, et al. Constructing road safety performance indicators using fuzzy delphi method and grey delphi method[J]. Expert Systems with Applications, 2011, 38(3): 1509-1514. [本文引用:1] [JCR: 1.854]
[11]	侯树展, 孙小瑞, 贺玉龙, 等. 高速公路交通事故严重程度与交通流特征的关系研究[J]. 中国安全科学学报, 2011(9): 106-111. Hou Shu-zhan, Sun Xiao-rui, He Yu-long, et al. Relationships between crash severity and traffic flow characteristics on freeways[J]. China Safety Science Journal, 2011(9): 106-111. [本文引用:1] [CJCR: 1.327]
[12]	Mussone L, Ferrari A, Oneta M. An analysis of urban collisions using an artificial intelligence model[J]. Accident Analysis & Prevention, 1999, 31(6): 705-718. [本文引用:1]
[13]	Chang L Y, Wang H W. Analysis of traffic injury severity: an application of non-parametric classification tree techniques[J]. Accident Analysis & Prevention, 2006, 38(5): 1019-1027. [本文引用:1]
[14]	de Ona J, Mujalli R O, Calvo F J. Analysis of traffic accident injury severity on Spanish rural highways using Bayesian networks[J]. Accident Analysis and Prevention, 2011, 43(1): 402-411. [本文引用:1]
[15]	Delen D, Sharda R, Bessonov M. Identifying significant predictors of injury severity in traffic accidents using a series of artificial neural networks[J]. Accident Analysis & Prevention, 2006, 38(3): 434-444. [本文引用:1]
[16]	Xie Yuan-chang, Lord Dominique, Zhang Yun-long. Predicting motor vehicle collisions using bayesian neural network models: an empirical analysis[J]. Accident Analysis & Prevention, 2011, 43(1): 402-411. [本文引用:1]
[17]	de Oña Juan, Mujalli Rand a Oqab, Calvo Francisco J. Analysis of traffic accident injury severity on spanish rural highways using bayesian networks[J]. Accident Analysis & Prevention, 2007, 39(5): 922-933. [本文引用:1]
[18]	Li X G, Lord D, Zhang Y L, et al. Predicting motor-vehicle crashes using support vector machine models[J]. Accident Analysis & Prevention, 2008, 40(4): 1611-1618. [本文引用:1]
[19]	田英杰. 支持向量回归机及其应用研究[D]. 北京: 中国农业大学经济管理学院, 2005. Tian Ying-jie. Support vector regression and its application[D]. Beijing: College of Economics & Management, China Agricultural University, 2005. [本文引用:1]
[20]	奉国和. SVM分类核函数及参数选择比较[J]. 计算机工程与应用, 2011, 47(3): 123-128. Feng Guo-he. Parameter optimizing for support vector machines classification[J]. Computer Engineering and Applications, 2011, 47(3): 123-128. [本文引用:1] [CJCR: 0.457]
[21]	董国君, 哈力木拉提·买买提, 余辉. 基于RBF核的SVM核参数优化算法[J]. 新疆大学学报: 自然科学版, 2009(3): 355-358. Dong Guo-jun, Halmurat Maimait, Yu Hui. Algorithms of optimizing SVM's kernel parameters with RBF kernel[J]. Journal of Xinjiang University(Natural Science Edition), 2009(3): 355-358. [本文引用:1] [CJCR: 0.1793]
[22]	徐崇刚, 胡远满, 常禹, 等. 生态模型的灵敏度分析[J]. 应用生态学报, 2004, 15(6): 1056-1062. Xu Chong-gang, Hu Yuan-man, Chang Yu, et al. Sensitivity analysis of ecological modeling[J]. Chinese Journal of Applied Ecology, 2004, 15(6): 1056-1062. [本文引用:1] [CJCR: 1.742]
[23]	Li Zhi-bin, Liu Pan, Wang Wei, et al. Using support vector machine models for crash injury severity analysis[J]. Accident Analysis & Prevention, 2012(45): 478-486. [本文引用:1]
[24]	GA/T859-2010. 中华人民共和国公安部. 道路交通事故处理信息数据结构[S]. [本文引用:1]

2011

0.0

. 2011, 43(5):1666-1676 DOI:10.1016/j.aap.2011.03.025

The statistical analysis of highway crash-injury severities: A review and assessment of methodological alternatives

Abstract Reducing the severity of injuries resulting from motor-vehicle crashes has long been a primary emphasis of highway agencies and motor-vehicle manufacturers. While progress can be simply measured by the reduction in injury levels over time, insights into the effectiveness of injury-reduction technologies, policies, and regulations require a more detailed empirical assessment of the complex interactions that vehicle, roadway, and human factors have on resulting crash-injury severities. Over the years, researchers have used a wide range of methodological tools to assess the impact of such factors on disaggregate-level injury-severity data, and recent methodological advances have enabled the development of sophisticated models capable of more precisely determining the influence of these factors. This paper summarizes the evolution of research and current thinking as it relates to the statistical analysis of motor-vehicle injury severities, and provides a discussion of future methodological directions. Highlights ? This paper provides a state-of-the-practice review of statistical methods for analyzing crash-injury severity data. ? Methodological issues germane to the analysis of injury severity data are discussed. ? Appropriate techniques for addressing these methodological issues are described. ? These techniques range from simple, binary outcome models to more sophisticated models allowing for heterogeneous effects and correlated error terms. ? Areas of opportunity for future research are highlighted based upon advances in computing and richer data sources.

... 0 引言目前,国内外已经在道路交通事故严重程度影响因素分析领域开展了广泛研究,其中以经典统计模型的相关应用最为广泛^[1],如二项或多项Logit、Probit模型^[2,3],有序Logit、Probit或贝叶斯模型^[4,5],嵌套Logit模型^[6],混合Logit模型^[7]等 ...

... 但SVM方法长于处理小样本、非线性以及高维的分类识别问题,建模过程损失了特征变量对分类精度敏感程度的可解释性^[1],因此,本文通过计算各影响因素的单变量局部灵敏度,获得特征变量重要性排序^[18],并通过观察特征变量组合发掘城市道路交通事故严重程度规律,提出相应预防对策和控制措施 ...

2006

0.863

0.0

2010

0.0

. 2010, 42(1):131-139 DOI:10.1016/j.aap.2009.07.013

Empirical assessment of the impact of highway design exceptions on the frequency and severity of vehicle accidents

Abstract Compliance to standardized highway design criteria is considered essential to ensure roadway safety. However, for a variety of reasons, situations arise where exceptions to standard-design criteria are requested and accepted after review. This research explores the impact that such design exceptions have on the frequency and severity of highway accidents in Indiana. Data on accidents at carefully selected roadway sites with and without design exceptions are used to estimate appropriate statistical models of the frequency and severity of accidents at these sites using recent statistical advances with mixing distributions. The results of the modeling process show that presence of approved design exceptions has not had a statistically significant effect on the average frequency or severity of accidents – suggesting that current procedures for granting design exceptions have been sufficiently rigorous to avoid adverse safety impacts. However, the findings do suggest that the process that determines the frequency of accidents does vary between roadway sites with design exceptions and those without.

2004

0.0

. 2004, 36(5):869-876 DOI:10.1016/j.aap.2003.09.002

Bivariate ordered-response probit model of driver's and passenger's injury severities in collisions with fixed objects

Abstract A bivariate ordered-response probit model of driver’s and most severely injured passenger’s severity (IS) in collisions with fixed objects is developed in this study. Exact passenger’s IS is not necessarily observed, especially when only most severe injury of the accident and driver’s injury are recorded in the police reports. To accommodate passenger IS as well, we explicitly develop a partial observability model of passenger IS in multi-occupant vehicle (HOV). The model has consistent coefficients for the driver IS between single-occupant vehicle (SOV) and multiple-occupant vehicle accidents, and provides more efficient coefficient estimates by taking into account the common unobserved factors between driver and passenger IS. The results of the empirical analysis using 4-year statewide accident data in Washington State reveal the effects of driver’s characteristics, vehicle attributes, types of objects, and environmental conditions on both driver and passenger IS, and that their IS have different elasticities to some of the risk factors.

2008

0.0

. 2008, 40(1):45-54 DOI:10.1016/j.aap.2007.04.002

Severity of driver injury and vehicle damage in traffic crashes at intersections: a Bayesian hierarchical analysis

Abstract Most crash severity studies ignored severity correlations between driver–vehicle units involved in the same crashes. Models without accounting for these within-crash correlations will result in biased estimates in the factor effects. This study developed a Bayesian hierarchical binomial logistic model to identify the significant factors affecting the severity level of driver injury and vehicle damage in traffic crashes at signalized intersections. Crash data in Singapore were employed to calibrate the model. Model fitness assessment and comparison using intra-class correlation coefficient (ICC) and deviance information criterion (DIC) ensured the suitability of introducing the crash-level random effects. Crashes occurring in peak time and in good street-lighting condition as well as those involving pedestrian injuries tend to be less severe. But crashes that occur in night time, at T/Y type intersections, and on right-most lane, as well as those that occur in intersections where red light cameras are installed tend to be more severe. Moreover, heavy vehicles have a better resistance on severe crash and thus induce less severe injuries, while crashes involving two-wheel vehicles, young or aged drivers, and the involvement of offending party are more likely to result in severe injuries.

2002

0.0

. 2002, 34(2):149-161 DOI:10.1016/S0001-4575(01)00009-4

Impact of roadside features on the frequency and severity of run-off-roadway accidents: an empirical analysis

Abstract In the US, single-vehicle run-off-roadway accidents result in a million highway crashes with roadside features every year and account for approximately one-third of all highway fatalities. Despite the number and severity of run-off-roadway accidents, quantification of the effect of possible countermeasures has been surprisingly limited due to the absence of data (particularly data on roadside features) needed to rigorously analyze factors affecting the frequency and severity of run-off-roadway accidents. This study provides some initial insight into this important problem by combining a number of databases, including a detailed database on roadside features, to analyze run-off-roadway accidents on a 96.6-km section of highway in Washington State. Using zero-inflated count models and nested logit models, statistical models of accident frequency and severity are estimated and the findings isolate a wide range of factors that significantly influence the frequency and severity of run-off-roadway accidents. The marginal effects of these factors are computed to provide an indication on the effectiveness of potential countermeasures. The findings show significant promise in applying new methodological approaches to run-off-roadway accident analysis.

2008

0.0

. 2008, 40(3):1033-1054 DOI:10.1016/j.aap.2007.11.010

A mixed generalized ordered response model for examining pedestrian and bicyclist injury severity level in traffic crashes

Abstract This paper proposes an econometric structure for injury severity analysis at the level of individual accidents that recognizes the ordinal nature of the categories in which injury severity are recorded, while also allowing flexibility in capturing the effects of explanatory variables on each ordinal category and allowing heterogeneity in the effects of contributing factors due to the moderating influence of unobserved factors. The model developed here, referred to as the mixed generalized ordered response logit (MGORL) model, generalizes the standard ordered response models used in the extant literature for injury severity analysis. To our knowledge, this is the first such formulation to be proposed and applied in the econometric literature in general, and in the safety analysis literature in particular. The MGORL model is applied to examine non-motorist injury severity in accidents in the USA, using the 2004 General Estimates System (GES) database. The empirical findings emphasize the inconsistent results obtained from the standard ordered response model. An important policy result from our analysis is that the general pattern and relative magnitude of elasticity effects of injury severity determinants are similar for pedestrians and bicyclists. The analysis also suggests that the most important variables influencing non-motorist injury severity are the age of the individual (the elderly are more injury-prone), the speed limit on the roadway (higher speed limits lead to higher injury severity levels), location of crashes (those at signalized intersections are less severe than those elsewhere), and time-of-day (darker periods lead to higher injury severity).

0.0

. , 2009(3):168-171

Prediction model cumulative logistic for severity of road traffic accident

为了分析交叉口交通事故严重程度的影响因素,在对北京周边无信号三路交叉口交通事故数据调查的基础上,建立的累积Logistic模型,可为我国交叉口严重交通事故的预防提供科学依据.模型分析结果表明,交叉口转弯车辆比例、控制方式和土地开发强度时无信号三路交叉口交通事故的严重程度有显著影响.

... 国内学者李世民等^[8]利用累积Logit模型研究了交叉口交通事故严重程度与转弯车辆、用地性质等因素的关系 ...

2010

0.0

0.701

. 2010, 40(2):423-426

Analysis of factors affecting accident severity in highway tunnels based on logistic model

School of Traffic &|Transportation|Beijing Jiaotong University|Beijing 100044|China

Based on the traffic accident data collected from the 4 tunnels in Shaoguan section of Beijingzhuhai freeway, taking the accident severity as dependent variable, selecting 9 candidate independent variables from 3 aspects: the time of the accident happened, the tunnel environment, and the traffic dynamic factors, the relevance between the candidate independent variables and the dependent variable was analyzed by the reverse selection method. It was found that the time of the accident happened, the collision type, the weather condition, and the ratio of daily PCU to AADT are the factors that most significantly related to the accident severity. The effects of these most related factors on the accident severity was analyzed using a logistic regression model. A statistical interpretation was given to the modeled estimates in terms of the odds ratio concept. The proposed logistic regression model was tested on the goodnessoffit and predictive accuracy and the encouraging result was achieved.

根据京珠高速公路韶关段4个隧道的交通事故资料，以事故严重程度为因变量，从时间、隧道环境和交通动态因素3个方面选择9个候选自变量，采用反向选择法分析候选自变量与因变量是否显著相关。研究发现：事故发生时段、碰撞类型、天气和日标准小客车交通量与年平均日交通量（AADT）之比与事故严重程度显著相关。采用logistic回归模型，分析了事故发生时段、碰撞类型、天气和日标准小客车交通量与AADT之比对交通事故严重程度的影响程度，并根据发生比率的概念，对模型的估计情况进行了解释。最后，从模型的拟合优度和预测准确度2个方面对模型进行检验。结果表明，建立的logistic回归模型在事故严重程度影响因素分析中具有较好的适应性和实用性。

... 马壮林等^[9,10]分别利用累积Logit模型和灰色模型研究了道路设计因素对隧道交通事故严重程度的影响 ...

2011

1.854

0.0

. 2011, 38(3):1509-1514 DOI:10.1016/j.eswa.2010.07.062

Constructing road safety performance indicators using fuzzy delphi method and grey delphi method

Abstract The main goal of this paper is to construct three sets of road safety performance indicators, which are regional road safety performance indicators, urban road safety performance indicators and highway safety performance indicators, respectively. Fuzzy Delphi Method and Grey Delphi Method are applied to quantify experts’ attitudes to regional road safety, urban road safety and highway safety. Comparing the results of two methods, the different results of two methods are analyzed, and then the final safety performance indicators are obtained by taking the intersection of results of two methods. Finally, three sets of performance indicators are constructed, which can be described and evaluated the safety level of region, urban road and highway, respectively. The research findings show that the method used in this paper is feasible and practical and can be provided as a reference for the administrative authority of road safety.

... 马壮林等^[9,10]分别利用累积Logit模型和灰色模型研究了道路设计因素对隧道交通事故严重程度的影响 ...

0.0

1.327

... 侯树展等^[11]利用主成分分析法研究了交通流特征和高速公路事故严重程度之间的联系 ...

1999

0.0

... 考虑到经典统计模型的缺陷和不足^[12],近年来有学者开始尝试将非参数、人工智能方法应用于交通事故严重程度影响因素分析,代表性的如分类回归树模型^[13],贝叶斯网络模型^[14],神经网络模型^[15]等 ...

2006

0.0

. 2006, 38(5):1019-1027 DOI:10.1016/j.aap.2006.04.009

Analysis of traffic injury severity: an application of non-parametric classification tree techniques

Abstract Statistical regression models, such as logit or ordered probit/logit models, have been widely employed to analyze injury severity of traffic accidents. However, most regression models have their own model assumptions and pre-defined underlying relationships between dependent and independent variables. If these assumptions are violated, the model could lead to erroneous estimations of injury likelihood. The classification and regression tree (CART), one of the most widely applied data mining techniques, has been commonly employed in business administration, industry, and engineering. CART does not require any pre-defined underlying relationship between target (dependent) variable and predictors (independent variables) and has been shown to be a powerful tool, particularly for dealing with prediction and classification problems. This study uses the 2001 accident data for Taipei, Taiwan. A CART model was developed to establish the relationship between injury severity and driver/vehicle characteristics, highway/environmental variables and accident variables. The results indicate that the most important variable associated with crash severity is the vehicle type. Pedestrians, motorcycle and bicycle riders are identified to have higher risks of being injured than other types of vehicle drivers in traffic accidents.

2011

0.0

. 2011, 43(1):402-411 DOI:10.1016/j.aap.2010.09.010

Analysis of traffic accident injury severity on Spanish rural highways using Bayesian networks

Abstract Several different factors contribute to injury severity in traffic accidents, such as driver characteristics, highway characteristics, vehicle characteristics, accidents characteristics, and atmospheric factors. This paper shows the possibility of using Bayesian Networks (BNs) to classify traffic accidents according to their injury severity. BNs are capable of making predictions without the need for pre assumptions and are used to make graphic representations of complex systems with interrelated components. This paper presents an analysis of 1536 accidents on rural highways in Spain, where 18 variables representing the aforementioned contributing factors were used to build 3 different BNs that classified the severity of accidents into slightly injured and killed or severely injured. The variables that best identify the factors that are associated with a killed or seriously injured accident (accident type, driver age, lighting and number of injuries) were identified by inference. Research highlights ? Bayesian Networks are usefully applied in the domain of traffic accident modeling. ? BNs are used for classifying traffic accidents according to their injury severity. ? BNs inference identifies variables associated with KSI (killed or seriously injured). ? The key variables for KSI were accident type, age, lighting and number of injuries.

2006

0.0

. 2006, 38(3):434-444 DOI:10.1016/j.aap.2005.06.024

Identifying significant predictors of injury severity in traffic accidents using a series of artificial neural networks

Abstract Understanding the circumstances under which drivers and passengers are more likely to be killed or more severely injured in an automobile accident can help improve the overall driving safety situation. Factors that affect the risk of increased injury of occupants in the event of an automotive accident include demographic or behavioral characteristics of the person, environmental factors and roadway conditions at the time of the accident occurrence, technical characteristics of the vehicle itself, among others. This study uses a series of artificial neural networks to model the potentially non-linear relationships between the injury severity levels and crash-related factors. It then conducts sensitivity analysis on the trained neural network models to identify the prioritized importance of crash-related factors as they apply to different injury severity levels. In the process, the problem of five-class prediction is decomposed into a set of binary prediction models (using a nationally representative sample of 30 358 police-recorded crash reports) in order to obtain the granularity of information needed to identify the “true” cause and effect relationships between the crash-related factors and different levels of injury severity. The results, mostly validated by the findings of previous studies, provide insight into the changing importance of crash factors with the changing injury severity levels.

2011

0.0

. 2011, 43(1):402-411 DOI:10.1016/j.aap.2010.09.010

Predicting motor vehicle collisions using bayesian neural network models: an empirical analysis

... 研究表明,非参数模型在实证研究中具有更优的统计拟合度和泛化能力^[16,17] ...

2007

0.0

. 2007, 39(5):922-933 DOI:10.1016/j.aap.2006.12.014

Analysis of traffic accident injury severity on spanish rural highways using bayesian networks

Abstract Statistical models have frequently been used in highway safety studies. They can be utilized for various purposes, including establishing relationships between variables, screening covariates and predicting values. Generalized linear models (GLM) and hierarchical Bayes models (HBM) have been the most common types of model favored by transportation safety analysts. Over the last few years, researchers have proposed the back-propagation neural network (BPNN) model for modeling the phenomenon under study. Compared to GLMs and HBMs, BPNNs have received much less attention in highway safety modeling. The reasons are attributed to the complexity for estimating this kind of model as well as the problem related to “over-fitting” the data. To circumvent the latter problem, some statisticians have proposed the use of Bayesian neural network (BNN) models. These models have been shown to perform better than BPNN models while at the same time reducing the difficulty associated with over-fitting the data. The objective of this study is to evaluate the application of BNN models for predicting motor vehicle crashes. To accomplish this objective, a series of models was estimated using data collected on rural frontage roads in Texas. Three types of models were compared: BPNN, BNN and the negative binomial (NB) regression models. The results of this study show that in general both types of neural network models perform better than the NB regression model in terms of data prediction. Although the BPNN model can occasionally provide better or approximately equivalent prediction performance compared to the BNN model, in most cases its prediction performance is worse than the BNN model. In addition, the data fitting performance of the BPNN model is consistently worse than the BNN model, which suggests that the BNN model has better generalization abilities than the BPNN model and can effectively alleviate the over-fitting problem without significantly compromising the nonlinear approximation ability. The results also show that BNNs could be used for other useful analyses in highway safety, including the development of accident modification factors and for improving the prediction capabilities for evaluating different highway design alternatives.

... 研究表明,非参数模型在实证研究中具有更优的统计拟合度和泛化能力^[16,17] ...

2008

0.0

. 2008, 40(4):1611-1618 DOI:10.1016/j.aap.2008.04.010

Predicting motor-vehicle crashes using support vector machine models

Abstract Crash prediction models have been very popular in highway safety analyses. However, in highway safety research, the prediction of outcomes is seldom, if ever, the only research objective when estimating crash prediction models. Only very few existing methods can be used to efficiently predict motor vehicle crashes. Thus, there is a need to examine new methods for better predicting motor vehicle crashes. The objective of this study is to evaluate the application of Support Vector Machine (SVM) models for predicting motor vehicle crashes. SVM models, which are based on the statistical learning theory, are a new class of models that can be used for predicting values. To accomplish the objective of this study, Negative Binomial (NB) regression and SVM models were developed and compared using data collected on rural frontage roads in Texas. Several models were estimated using different sample sizes. The study shows that SVM models predict crash data more effectively and accurately than traditional NB models. In addition, SVM models do not over-fit the data and offer similar, if not better, performance than Back-Propagation Neural Network (BPNN) models documented in previous research. Given this characteristic and the fact that SVM models are faster to implement than BPNN models, it is suggested to use these models if the sole purpose of the study consists of predicting motor vehicle crashes.

2005

0.0

. 2005, :-

Support vector regression and its application

... 1 SVM基本思想与核参数寻优基于统计学习理论的结构风险最小化原则的SVM方法,基本思想是通过非线性变换将高维空间线性决策函数代替原样本属性空间非线性决策函数^[19],最终求解凸二次规划问题,保证解值的唯一性和全局最优性 ...

2011

0.0

0.457

. 2011, 47(3):123-128 DOI:10.3778/j.issn.1002-8331.2011.03.037

Parameter optimizing for support vector machines classification

School of Economy & Manangement，South China Normal University，Guangzhou 510006，China

Support Vector Machine（SVM） has good performance for classification，but the performance is restricted by the kernel function and its parameters.This paper discusses the problem，and uses cross validation，grid searching for optimizing the kernel function parameters.

支持向量机（SVM）被证实在分类领域性能良好，但其分类性能受到核函数及参数影响。讨论核函数及参数对SVM分类性能的影响，并运用交叉验证与网格搜索法进行参数优化选择，为SVM分类核函数及参数选择提供借鉴。

... 此外,惩罚参数C与RBF核函数参数g的选取很大程度上影响着SVM模型的分类识别效果^[20] ...

0.0

0.1793

. , 2009(3):355-358

Algorithms of optimizing SVM's kernel parameters with RBF kernel

SVM是一种新型的机器学习方法,其分类性能的优劣主要受核函数及核参数的影响,国内外学者针对SVM核参数的选择已提出许多算法.本文首先分析了RBF核参数对SVM分类性能的影响,然后又对比分析了目前存在的几种基于RBF核的SVM核参数选择方法.通过实验.发现使用遗传算法选择核参数的SVM有比较快的搜索速度.

... 许多研究者针对SVM建模的参数寻优提出了各自的算法,常见算法有网格搜索法、双线性搜索法、梯度下降法、拟牛顿法、蒙特卡罗法、遗传算法等^[21],本文分别采用网格法和遗传算法对惩罚参数C和RBF核参数g进行参数寻优,最终选取K-CV条件下测试集精度最高和C值最小的一组作为寻优结果 ...

2004

0.0

1.742

... 具体分析方法主要包括局部灵敏度分析和全局灵敏度分析^[22] ...

0.0

... 城市道路交通事故严重程度影响因素特征变量多为二值或多值分类变量及少数连续变量^[23],适用于单因素局部灵敏度分析 ...

0.0

... 城市道路交通事故影响因素特征变量取自“事故基本信息”数据集,主要包括事故自身属性、致因属性、时空属性和行政属性等,其数据结构为事故现场信息代码^[24] ...