基于微分方程组的多排桩内力分析

引用本文

张庆, 王磊. 基于微分方程组的多排桩内力分析. 吉林大学学报: 工学版, 2014, 44(5): 1327-1333[ZHANG Qing, WANG Lei. Internal force analysis of multiple rows of piles based on differential equation set. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1327-1333] 复制到剪切板

Permissions

基于微分方程组的多排桩内力分析

张庆^1,², 王磊¹

1.吉林大学建设工程学院, 长春 130022

2.吉林建筑大学土木工程学院, 长春 130118

作者简介:张庆（1980-）,男,博士研究生,讲师.研究方向:基础结构计算.E-mail:zhang_qing_z@126.com

基金:“973”国家重点基础研究发展计划项目（2010CB731503）

摘要

在基础工程中依据弹性地基梁模型,建立了桩的荷载-内力-变形微分关系式,将多排桩的每个桩构件依据微分关系式的不同分别划分为一组杆件,每个杆件建立一个微分方程,全部微分方程集成一个微分方程组,依据边界条件及杆件连接点的变形协调、内力平衡条件求解微分方程组,得出多排桩的内力和变形,最后通过实例验证了本文方法适用于多排桩的内力分析。

关键词: 工程力学; 多排桩; 微分方程组; 内力分析

中图分类号:TU473.1 文献标志码:A 文章编号:1671-5497(2014)05-1327-07

Internal force analysis of multiple rows of piles based on differential equation set

ZHANG Qing^1,², WANG Lei¹

1.College of Construction Engineering, Jilin University, Changchun 130022,China

2.School of Civil Engineering, Jilin Jianzhu University, Changchun 130118, China

Abstract

Base on the elastic foundation beam model in the foundation work, the differential relationship of the load-internal force-deformation of the piles is established. Each pile component of the multi rows of the piles is divided into a group of bars according to different differential equation. A differential equation is established for each bar, and all the equations are integrated into a differential equation set. The internal force and deformation of the multiple rows of piles are obtained according to the boundary condition, the deformation compatibility of the bar node and the balance conditions of the internal force. Case study is carried out and the results verify the feasibility of the proposed method for internal force analysis of multiple rows of piles.

Keyword: engineering mechanics; multiple rows of piles; differential equation set; internal force analysis

Show Figures

0 引言

桥梁的桩基础承担横向荷载,桩基础的内力计算较多采用弹性地基梁法^{[ 1]},弹性地基梁模型求解方法有半解析法(幂级数、积分方程解、微分算子解)、有限元方法以及有限差分法。计算过程繁琐,摩擦桩、支撑桩的系数不同,计算过程中要引用不同系数、查不同的表格,桩顶自由度和弹性嵌固的计算也要引用不同公式、查不同的表格^{[ 1]},整个公式推导过程复杂。

许多研究人员对桩群承受横向荷载的计算方法进行了研究,Poulo^{[ 2, 3]}采用相互作用系数方法分析水平荷载作用下的群桩问题;Pak^{[ 4]}基于虚拟桩模型建立了均质地基中横向受荷桩的求解方法;周洪波等^{[ 5]}提出了能够考虑群桩效应和群桩中各桩荷载分担比的改进公式;王伟^{[ 6]}利用变分原理和最小势能原理推导得出群桩刚度矩阵的表达式;孙勇^{[ 7]}提出了滑动面以下考虑滑坡体存在的两种新的m法;袁志林等^{[ 8]}提出了有效模拟桩基水平承载特性的有限元模型。研究表明,桩群的计算方法基本上都需要通过实验数据、数值分析和有限元方法改进传统查表方法,通过研究减少了繁琐的查表过程,但是需要运用大量的数理知识和有限元方法实现,不利于实际工程的应用。

由于桩的荷载集度与位移的关系方程是微分方程的形式,利用微分方程求解多排桩的内力问题是可行的,但是微分方程中的变量不同,不同桩的表达式也不尽相同,或者单个桩的不同部位也不相同,根据微分方程的不同,将单桩划分为不同的计算杆件,每个杆件建立自身的微分方程,再将多排桩的所有微分方程联立成微分方程组,确定微分方程组以及边界条件,计算微分方程组,得到多排桩的内力和位移,相比于其他方法,减少了大量的数值分析和有限元仿真等过程,只是利用简单的数学软件Maple实现,并且Maple的计算过程只需进行简单的编程,根据工程的实际情况,对编程进行局部调整即可,计算过程简单,计算结果准确,有利于实际工程应用。

1 多排桩微分方程组的建立

1.1 桩的法向变形微分方程

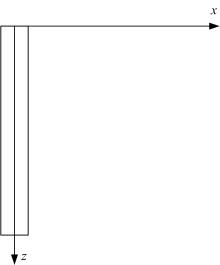
假设桩侧土为文克尔离散线性弹簧,不考虑桩土之间的黏着力和摩阻力,桩作为弹性构件考虑,桩的位移坐标系如图1所示,依据材料力学可知桩的挠曲微分方程如下:

$\begin{matrix} EI \frac{d^{4} x_{z}}{d z^{4}} + mz x_{z} b_{1} = 0 (1) \end{matrix}$

式中: $\begin{matrix} m \end{matrix}$ 为“m”法系数; $\begin{matrix} b_{1} \end{matrix}$ 为杆件计算宽度; $\begin{matrix} E \end{matrix}$ 为杆件弹性模量; $\begin{matrix} I \end{matrix}$ 为杆件横截面惯性矩。

	Figure Option View Download New Window
	图1 桩位移坐标系示意图Fig.1 Diagram of pile displacement coordinate system

1.2 桩的轴向变形微分方程

对于杆件有:

$\begin{matrix} ε = \frac{N (z)}{EA} = \frac{du}{dz} (2) \end{matrix}$

桩身受桩轴力 $\begin{matrix} N (z) \end{matrix}$ 为变值:

$\begin{matrix} N (z) = P - τ_{h} z (3) \end{matrix}$

式中: $\begin{matrix} P \end{matrix}$ 为桩顶竖向荷载; $\begin{matrix} τ_{h} \end{matrix}$ 为桩侧摩阻力。

当桩侧摩阻力呈三角形分布时:

$\begin{matrix} τ_{h} = \frac{2 Pz}{U h^{2}} (4) \end{matrix}$

式中: $\begin{matrix} U \end{matrix}$ 为桩的周长; $\begin{matrix} h \end{matrix}$ 为桩的高度。

当桩侧摩阻力呈均匀分布时:

$\begin{matrix} τ_{h} = \frac{P}{U h} (5) \end{matrix}$

结合前面的公式可以确定位移与桩顶荷载之间的关系式,对于桩侧摩阻力三角形分布情况:

$\begin{matrix} \frac{du}{dz} = P \frac{(1 - \frac{2 z^{2}}{U h^{2}})}{EA} (6) \end{matrix}$

对于桩侧摩阻力均匀分布情况:

$\begin{matrix} \frac{du}{dz} = \frac{P}{EA} (1 - \frac{z}{U h}) (7) \end{matrix}$

式(6)(7)即为桩的轴向变形微分方程,应用于多排桩的计算。

1.3 微分方程组的建立

柱-桩结构中柱和桩的微分方程不同,同样是桩可能因为土层的不同 $\begin{matrix} m \end{matrix}$ 值不同,柱中直径一般要发生变化,即 $\begin{matrix} I \end{matrix}$ 不同,材料发生变化时 $\begin{matrix} E \end{matrix}$ 也会发生变化。柱中要承受外荷载,如果有集中力时 $\begin{matrix} Q 值发生突变, 有集中力矩时 M \end{matrix}$ 值发生突变,以上的各种情况微分方程或者微分方程组的表达式都会发生变化,根据实际特点分别建立微分方程,全部微分方程集成一个微分方程组,该微分方程组全面反映柱-桩受横向荷载时的内力与变形,在实际工程应用中需要根据实际情况划分杆件,建立每个杆件的法向变形和轴向变形的微分方程,法向变形的微分方程一般分为两种情况:

$\begin{matrix} \{\begin{matrix} E_{ij} I_{ij} \frac{d^{4} x_{z}}{d z^{4}} + mz x_{z} b_{ij} = 0 \\ E_{ij} I_{ij} \frac{d^{4} x_{z}}{d z^{4}} = 0 \end{matrix} (8) \end{matrix}$

轴向变形微分方程一般分为3种情况:

$\begin{matrix} \{\begin{matrix} E_{ij} A_{ij} \frac{d^{2} u (z)}{d z^{2}} = 0 \\ E_{ij} A_{ij} \frac{d^{3} u (z)}{d z^{3}} = 0 \\ E_{ij} A_{ij} \frac{d^{4} u (z)}{d z^{4}} = 0 \end{matrix} (9) \end{matrix}$

全部杆件的法向变形和轴向变形联立组成微分方程组,依据微分方程组进行内力分析。研究人员的研究大多集中在单个微分方程的求解,本文依据构件特点划分杆件,建立杆件的微分方程集成微分方程组并求解。

2 多排桩边界条件

2.1 桩底边界条件

2.1.1 摩擦桩

摩擦桩桩底用转角与桩底的土抗力建立一个边界条件,用微分方程的形式表示, $\begin{matrix} z = h \end{matrix}$ 时:

$\begin{matrix} EI \frac{d^{2} x_{z}}{d z^{2}} = - \frac{d x_{z}}{dz} C_{0} I_{0} (10) \end{matrix}$

由于认为摩擦桩桩底面剪力为零,即 $\begin{matrix} z = h \end{matrix}$ 时:

$\begin{matrix} EI \frac{d^{3} x_{z}}{d z^{3}} = 0 (11) \end{matrix}$

当摩擦桩 $\begin{matrix} α h > 2.5 \end{matrix}$ 或支承桩 $\begin{matrix} α h > 3.5 时 \end{matrix}$ 可认为:

$\begin{matrix} EI \frac{d^{2} x_{z}}{d z^{2}} = 0 (12) \end{matrix}$

式中: $\begin{matrix} I_{0} \end{matrix}$ 为桩底面积对其重心轴的惯性矩; $\begin{matrix} C_{0} \end{matrix}$ 为基底土的竖向地基系数, $\begin{matrix} C_{0} = m_{0} h 。 \end{matrix}$

2.1.2 嵌岩桩的边界条件

嵌岩桩桩底线位移和转角均为零,当 $\begin{matrix} z = h \end{matrix}$ 时,边界条件为:

$\begin{matrix} \{\begin{matrix} x_{z} = 0 \\ \frac{d x_{z}}{dz} = 0 \end{matrix} (13) \end{matrix}$

2.2 桩顶边界条件

2.2.1 桩顶自由

桩顶自由弯矩固定值 $\begin{matrix} C_{1}, \end{matrix}$ 剪力固定值 $\begin{matrix} C_{2}, C_{1} \end{matrix}$ 与 $\begin{matrix} C_{2} \end{matrix}$ 由上部结构计算。当 $\begin{matrix} z = - l \end{matrix}$ 时,- $\begin{matrix} l \end{matrix}$ 为桩顶标高,有:

$\begin{matrix} \{\begin{matrix} EI \frac{d^{2} x_{z}}{d z^{3}} = C_{1} \\ EI \frac{d^{3} x_{z}}{d z^{3}} = C_{2} \end{matrix} (14) \end{matrix}$

2.2.2 桩顶弹性嵌固

桩顶弹性嵌固时,转角为零、剪力为固定值 $\begin{matrix} C_{2}, C_{2} \end{matrix}$ 由上部结构得出。当 $\begin{matrix} z = - l \end{matrix}$ 时,有:

$\begin{matrix} \{\begin{matrix} \frac{d x_{z}}{dz} = 0 \\ EI \frac{d^{3} x_{z}}{d z^{3}} = C_{2} \end{matrix} (15) \end{matrix}$

2.3 桩竖向变形边界条件

桩对桩底土构成压缩,得到桩底的竖向位移 $\begin{matrix} u (h) \end{matrix}$ 与桩顶竖向位移 $\begin{matrix} u (0) \end{matrix}$ 的关系式:

$\begin{matrix} C_{0} A_{0} u (h) = EA \frac{du (0)}{dz} (16) \end{matrix}$

式中: $\begin{matrix} A_{0} \end{matrix}$ 为桩底面积。

2.4 桩与承台处边界协调条件

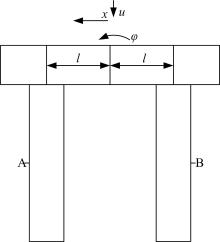
依据承台的刚性假设,承台只发生刚性平动和转动,承台与桩构件连接边界协调条件的示意图如图2所示,建立与承台相连桩的位移边界条件,承台为刚性,则各桩顶法向位移相等、转角相等。

$\begin{matrix} \{\begin{matrix} x_{zA} = x_{zB} \\ \frac{d x_{zA}}{dz} = \frac{d x_{zA}}{dz} \end{matrix} (17) \end{matrix}$

	Figure Option View Download New Window
	图2 承台与桩构件连接边界协调条件示意图Fig.2 Boundary compatibility condition of pile caps with pile components

桩顶轴向位移由承台竖向变形和承台转动引起,承台竖向变形引起的桩顶的竖向位移相等,转角引起桩顶竖向位移等于承台转角和桩顶到承台中心距离的乘积,建立变形协调关系式:

$\begin{matrix} u_{zA} - l \cdot \frac{d x_{zA}}{dz} = u_{zB} + l \cdot \frac{d x_{zB}}{dz} (18) \end{matrix}$

2.5 桩顶与承台顶的内力平衡关系

取承台为脱离体,承台与桩结构受力示意图如图3所示,建立水平、竖向、转动三个方向的平衡方程:

$\begin{matrix} \begin{matrix} E I_{A} \frac{d^{3} x_{zA}}{d z^{3}} + E I_{B} \frac{d^{3} x_{zB}}{d z^{3}} = Q (19) \\ E A_{A} \frac{d u_{A}}{dz} + E A_{B} \frac{d u_{B}}{dz} = P (20) \\ E A_{A} \frac{d u_{A}}{dz} l - E A_{B} \frac{d u_{B}}{dz} l + \\ E I_{A} \frac{d^{2} x_{zA}}{d z^{2}} + E I_{B} \frac{d^{2} x_{zB}}{d z^{2}} = M (21) \end{matrix} \end{matrix}$

式中: $\begin{matrix} M \end{matrix}$ 为节点所受集中弯矩; $\begin{matrix} Q \end{matrix}$ 为节点所受集中法向力; $\begin{matrix} P \end{matrix}$ 为节点所受集中轴向力。

	Figure Option View Download New Window
	图3 承台与桩结构受力示意图Fig.3 Force carried by pile caps and pile structure

2.6 边界条件总结

桩横向变形为四阶常微分方程,需要确定4个未定常数,横向的边界条件是两个桩底、两个桩顶一共4个边界条件,桩的轴向变形为一阶常微分方程,确认一个边界条件即可。

3 多排桩节点位移协调条件、内力平衡条件

3.1 变形协调条件

桩与桩之间均为刚性连接,构件连接示意图如图4所示,则变形协调条件位移与转角相等。

$\begin{matrix} \{\begin{matrix} x_{zA} = x_{zB} \\ \frac{d x_{zA}}{dz} = \frac{d x_{zB}}{dz} \\ u_{A} = u_{B} \end{matrix} (22) \end{matrix}$

	Figure Option View Download New Window
	图4 构件连接示意图Fig.4 Diagram of components connections

3.2 内力平衡条件

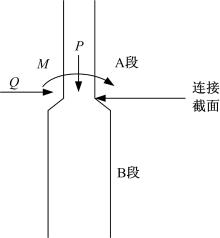
弯矩和剪力的正、负方向规定与材料力学相同,即剪力左面向上、右面向下为正,弯矩左面顺时针、右面逆时针为正,轴力压力为正、拉力为负,构件连接截面剪力、弯矩、轴力示意图如图5所示。

$\begin{matrix} \begin{matrix} E I_{A} \frac{d^{2} x_{zA}}{d z^{2}} = E I_{B} \frac{d^{2} x_{zB}}{d z^{2}} + M (23) \\ E I_{A} \frac{d^{3} x_{zA}}{d z^{3}} - E I_{B} \frac{d^{3} x_{zB}}{d z^{3}} = Q (24) \\ E A_{A} \frac{d u_{zA}}{dz} = E A_{B} \frac{d u_{zB}}{dz} + P (25) \end{matrix} \end{matrix}$

	Figure Option View Download New Window
	图5 构件连接截面剪力、弯矩、轴力示意图Fig.5 Shear force,bending moment,axial force of the component connected section

4 算例验证

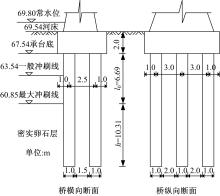
图6为双排式钢筋混凝土钻孔灌注桩桥墩基础荷载。上部为等跨30 m的钢筋混凝土预应力梁桥,荷载为纵向控制设计,作用于混凝土桥墩承台顶面桥纵向荷载如下。

	Figure Option View Download New Window
	图6 双排式灌注桩桥墩基础布置图Fig.6 Double-row bored pile pier foundation arrangement

恒载及一孔活载时:

$\begin{matrix} \begin{matrix} \sum N = 6791.40 kN, \\ \sum H = 358.60 kN, \\ \sum M = 4617.30 kN 。 \end{matrix} \end{matrix}$

恒载及二孔活载时,∑ N=7798.00 kN。

承台用C20混凝土,尺寸为2.0 m×4.5 m×8.0 m,作用在承台地面中心荷载如下:恒载加一孔活载(控制桩截面强度荷载)时,∑ N=8591.40 kN,∑ H=358.60 kN,∑ M=5334.50 kN。恒载加二孔活载(控制桩入土深度荷载)时,∑ N=9598.00 kN。

桩基础采用高桩承台式摩擦桩,桩拟采用直径 d=1.0 m,以冲抓锥施工。

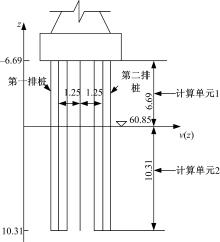
由于本算例桩体中部不产生荷载,设定最大冲刷线位置为零点,计算单元划分如图7所示,由于考虑了轴向变形对两排桩的作用效果不同,这样要区别轴向位移和法向位移的作用,区别前后两排桩的作用,设定第一排桩体计算单元1的轴向位移和法向位移分别为 $\begin{matrix} u_{11} (z) 、 v_{11} (z), \end{matrix}$ 计算单元2的轴向位移和法向位移分别为 $\begin{matrix} u_{10} (z) 、 v_{10} (z), \end{matrix}$ 同样第二排桩体计算单元1的轴向位移和法向位移分别为 $\begin{matrix} u_{21} (z) 、 v_{21} (z), \end{matrix}$ 计算单元2的轴向位移和法向位移为 $\begin{matrix} u_{20} (z) 、 v_{20} (z), \end{matrix}$ 之后通过受力特点和截面自身特点列出微分方程组如下:

$\begin{matrix} \{\begin{matrix} EA \frac{d^{2} u_{11} (z)}{d z^{2}} = 0 \\ EA \frac{d^{3} u_{10} (z)}{d z^{3}} = 0 \\ EI \frac{d^{4} v_{11} (z)}{d z^{4}} = 0 \\ EI \frac{d^{4} v_{10} (z)}{d z^{4}} + mb 1 v_{10} (z) z = 0 \\ EA \frac{d^{2} u_{21} (z)}{d z^{2}} = 0 \\ EA \frac{d^{3} u_{20} (z)}{d z^{3}} = 0 \\ E I \frac{d^{4} v_{21} (z)}{d z^{4}} = 0 \\ EI \frac{d^{4} v_{20} (z)}{d z^{4}} + mb 1 v_{20} (z) z = 0 \end{matrix} (26) \end{matrix}$

桩底的边界条件如下:

$\begin{matrix} \{\begin{matrix} C_{0} A_{0} u_{10} (10.31) = EA \frac{d u_{10} (0)}{dz} \\ EA \frac{d u_{10} (10.31)}{dz} = 0 \\ C_{0} A_{0} u_{20} (10.31) = EA \frac{d u_{20} (0)}{dz} \\ EA \frac{d u_{20} (10.31)}{dz} = 0 \\ EI \frac{d^{2} v_{10} (10.31)}{d z^{2}} = 0 \\ EI \frac{d^{3} v_{10} (10.31)}{d z^{3}} = 0 \\ EI \frac{d^{2} v_{20} (10.31)}{d z^{2}} = 0 \\ EI \frac{d^{3} v_{20} (10.31)}{d z^{3}} = 0 \end{matrix} (27) \end{matrix}$

桩顶的边界条件如下:

$\begin{matrix} \{\begin{matrix} v_{11} (- 6.69) = v_{21} (- 6.69) \\ \frac{d v_{11} (- 6.69)}{dz} = \frac{d v_{21} (- 6.69)}{dz} \\ \begin{matrix} u_{11} (- 6.69) - \frac{d v_{11} (- 6.69)}{dz} \times 1.25 = \\ u_{21} (- 6.69) + \frac{d v_{21} (- 6.69)}{dz} \times 1.25 \end{matrix} \\ \begin{matrix} 3 EA \frac{d u_{11} (- 6.69)}{dz} + \\ 3 EA \frac{d u_{21} (- 6.69)}{dz} = 8591.40 \end{matrix} \\ \begin{matrix} 3 EI \frac{d^{3} v_{11} (- 6.69)}{d z^{3}} + \\ 3 EI \frac{d^{3} v_{21} (- 6.6 9)}{d z^{3}} = 358.60 \end{matrix} \\ \begin{matrix} 3 EA \frac{d u_{11} (- 6.69)}{dz} \times 1.25 - \\ 3 EA \frac{d u_{21} (- 6.69)}{dz} \times 1.25 + \\ 3 EI \frac{d^{2} v_{11} (- 6.69)}{d z^{2}} + \\ 3 EI \frac{d^{2} v_{21} (- 6.69)}{d z^{2}} = 5334.50 \end{matrix} \end{matrix} (28) \end{matrix}$

	Figure Option View Download New Window
	图7 双排桩计算单元划分示意图Fig.7 Computing unit division of double-row piles

计算单元的连接节点的位移、轴力、转角、弯矩、剪力的条件如下:

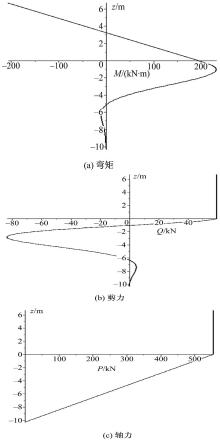
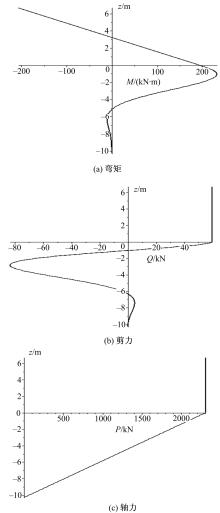
$\begin{matrix} \begin{matrix} \{\begin{matrix} u_{11} (0) = u_{10} (0) \\ u_{21} (0) = u_{20} (0) \end{matrix} (29) \\ \{\begin{matrix} v_{11} (0) = v_{10} (0) \\ v_{21} (0) = v_{20} (0) \end{matrix} (30) \\ \{\begin{matrix} EA \frac{d u_{11} (0)}{dz} = EA \frac{d u_{10} (0)}{dz} \\ EA \frac{d u_{21} (0)}{dz} = EA \frac{d u_{20} (0)}{dz} \end{matrix} (31) \\ \{\begin{matrix} \frac{d v_{11} (0)}{dz} = \frac{d v_{10} (0)}{dz} \\ \frac{d v_{21} (0)}{dz} = \frac{d v_{20} (0)}{dz} \end{matrix} (32) \\ \{\begin{matrix} EI \frac{d^{2} v_{11} (0)}{d z^{2}} = EI \frac{d^{2} v_{10} (0)}{d z^{2}} \\ EI \frac{d^{2} v_{21} (0)}{d z^{2}} = EI \frac{d^{2} v_{20} (0)}{d z^{2}} \end{matrix} (33) \\ \{\begin{matrix} EI \frac{d^{3} v_{11} (0)}{d z^{3}} = EI \frac{d^{3} v_{10} (0)}{d z^{3}} \\ EI \frac{d^{3} v_{21} (0)}{d z^{3}} = EI \frac{d^{3} v_{20} (0)}{d z^{3}} \end{matrix} (34) \end{matrix} \end{matrix}$

利用Maple求解工具进行求解并绘图,得到了第一排桩体法向位移的弯矩、剪力和轴力分布如图8所示。第二排桩体轴向位移的弯矩、剪力和轴力分布如图9所示。通过图形确定第一排桩局部冲刷线处弯矩、水平力、轴向力分别为 $\begin{matrix} M_{1} = 192.95 kN \cdot m 、 Q_{1} = 59.77 kN 、 P_{1} = 2308.672 kN 。 \end{matrix}$ 通过传统方法计算第一排桩的弯矩、水平力、轴向力分别为 $\begin{matrix} M_{0} = 192.51 kN \cdot m 、 Q_{0} = 59.76 kN 、 P_{0} = 2387.53 kN 。 \end{matrix}$ 由两种方法计算得到的弯矩、水平力、轴向力分别相差了0.2%、0.02%、3.3%,说明常微分方程组求解多排群桩结构是可行的。由于本文采用计算机计算,而传统方法是采用大量的手算过程与查表过程实现,因而常微分方程组计算误差更小,计算结果更为准确。

	Figure Option View Download New Window
	图8 第一排桩弯矩、剪力和轴力分布图Fig.8 Bending moment,shear force and axial force distribution of the first row of piles

	Figure Option View Download New Window
	图9 第二排桩弯矩、剪力和轴力分布图Fig.9 Bending moment,shear force and axial force distribution of the second row of piles

5 结束语

利用Maple软件进行微分方程组求解,得到了多排桩的内力图形,通过对内力图形进行分析,微分方程组的计算与通过规范方法进行计算的结果基本相同,说明利用微分方程组可以求解多排群桩的内力,计算过程简单,计算结果精确,便于实际工程应用。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	赵明华, 许学燕, 陈昌富, 等. 基础工程[M]. 北京: 高等教育出版社, 2010. [本文引用:2] [CJCR: 0.474]
[2]	Poulo S H G. Behavior of laterally-loaded piles: I -single piles[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1971, 97(5): 711-731. [本文引用:1]
[3]	Poulo S H G. Behaviour of laterally-loaded piles: II-pile groups[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1971, 97(5): 733-751. [本文引用:1]
[4]	Pak R Y S. On the flexure of a partially embedded bar under lateal loads[J]. Journal of Applied Mechanics, 1989, 56(2): 263-269. [本文引用:1] [JCR: 0.263]
[5]	周洪波, 茜平一, 杨波, 等. 水平荷载作用下群桩计算方法研究[J]. 工程勘察, 2000(1): 1-3. Zhou Hong-bo, Qian Ping-yi, Yang Bo, et al. Calculation methods study on cluster piles under horizontal loading[J]. Geotechnical Investigation &Surveying, 2000(1): 1-3. [本文引用:1] [CJCR: 0.2884]
[6]	王伟, 杨敏. 基于变分原理的群桩位移计算方法[J]. 岩土工程学报, 2005, 27(9): 1072-1076. Wang Wei, Yang Min. Vertical deformation analysis of pile group based on variational theory[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(9): 1072-1076. [本文引用:1] [CJCR: 0.989]
[7]	孙勇. 滑坡面下双排抗滑结构的计算方法研究[J]. 岩土力学, 2009, 30(10): 2971-2984. Sun Yong. Research on calculation method of double-row anti-sliding structure under sliding surfall[J]. Rock and Soil Mechanics, 2009, 30(10): 2971-2984. [本文引用:1] [CJCR: 0.879]
[8]	袁志林, 段梦兰, 陈祥余, 等. 水平荷载下导管架平台桩基础的非线性有限元分析[J]. 岩土力学, 2012, 33(8): 2551-2560. Yuan Zhi-lin, Duan Meng-lan, Chen Xiang-yu, et al. Nonlinear finite element analysis of jacket platform pile foundations under lateral loads[J]. Rock and Soil Mechanics, 2012, 33(8): 2551-2560. [本文引用:1] [CJCR: 0.879]

2010

0.0

0.474

... 0 引言桥梁的桩基础承担横向荷载,桩基础的内力计算较多采用弹性地基梁法^[1],弹性地基梁模型求解方法有半解析法(幂级数、积分方程解、微分算子解)、有限元方法以及有限差分法 ...

... 计算过程繁琐,摩擦桩、支撑桩的系数不同,计算过程中要引用不同系数、查不同的表格,桩顶自由度和弹性嵌固的计算也要引用不同公式、查不同的表格^[1],整个公式推导过程复杂 ...

1971

0.0

... 许多研究人员对桩群承受横向荷载的计算方法进行了研究,Poulo^[2,3]采用相互作用系数方法分析水平荷载作用下的群桩问题 ...

1971

0.0

... 许多研究人员对桩群承受横向荷载的计算方法进行了研究,Poulo^[2,3]采用相互作用系数方法分析水平荷载作用下的群桩问题 ...

1989

0.263

0.0

J. Appl. Mech.. 1989, 56(2):263-269

On the Flexure of a Partially Embedded Bar Under Lateral Loads

Ronald Y. S. Pak

University of Colorado, Boulder, Colo. 80309-0428

This investigation is concerned with a laterally-loaded bar which is partially embedded in a three-dimensional elastic half space. The loading is assumed to be applied at the unembedded end of the bar and may, in general, be a combination of horizontal shear forces and moments. On the adoption of a one-dimensional theory for the bar and the classical theory of elasticity for the semi-infinite solid, the structure-medium interaction problem is reduced to a Fredholm integral equation of the second kind whose solution is then computed. Selected results are presented to illustrate various features of the solution. A set of compliance charts is also included.

... Pak^[4]基于虚拟桩模型建立了均质地基中横向受荷桩的求解方法 ...

0.0

0.2884

... 周洪波等^[5]提出了能够考虑群桩效应和群桩中各桩荷载分担比的改进公式 ...

2005

0.0

0.989

. 2005, 27(9):1072-1076

Vertical deformation analysis of pile group based on variational theory

Department of Geotechnical Engineering Tongji University Shanghai 200092 China

Function with two undetermined coefficients was applied to characterize single pile displacement.Based on variational theory and minimum potential energy principle,analysis of pile group was deduced with the above function in order to get stiffness matrix of pile group.Displacement along pile length in pile group could be determined with the above stiffness matrix.Conclusion should be drawn after the comparison with other analysis methods that this method was as accurate as the other method,but less calculation was needed.The method have other advantage such as discretization of either soil or piles was not needed and solution procedure was rigorous for soil with stiffness increasing linearly with depth.

提出一个包含两个待定参数的群桩中单桩的位移函数关系式,由此利用变分原理和最小势能原理推导了群桩的分析过程,最终得出群桩刚度矩阵的表达式,进而可以求得群桩基础中任意单桩任意深度处的位移。通过各种分析方法对均匀土体和非均匀土体中群桩位移分析结果的比较说明该方法精度满足要求,但应用本文方法进行分析时不用划分桩土体单元,且计算量较小,能准确模拟土体模量随深度线性变化的情形。

... 王伟^[6]利用变分原理和最小势能原理推导得出群桩刚度矩阵的表达式 ...

2009

0.0

0.879

... 孙勇^[7]提出了滑动面以下考虑滑坡体存在的两种新的m法 ...

2012

0.0

0.879

... 袁志林等^[8]提出了有效模拟桩基水平承载特性的有限元模型 ...