表面测量中高斯滤波中线的有理逼近实现

引用本文

许景波, 袁怡宝, 崔晓萌, 郭欣, 王升. 表面测量中高斯滤波中线的有理逼近实现. 吉林大学学报: 工学版, 2014, 44(5): 1347-1352[XU Jing-bo, YUAN Yi-bao, CUI Xiao-meng, GUO Xin, WANG Sheng. Rational approximation implementation approach to determine Gaussian filtering mean line in surface roughness measurement. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1347-1352] 复制到剪切板

Permissions

表面测量中高斯滤波中线的有理逼近实现

许景波^1,², 袁怡宝³, 崔晓萌^1,², 郭欣^1,², 王升^1,²

1.哈尔滨理工大学测控技术与通信工程学院, 哈尔滨 150080

2.测控技术与仪器黑龙江省高校重点实验室, 哈尔滨 150080

3.哈尔滨工业大学自动化测试与控制系, 哈尔滨 150001

作者简介:许景波(1973-),男,副教授,博士.研究方向:高斯滤波器理论与应用,表面及圆度测量、滤波、评定技术.E-mail:hitxjb@126.com

基金:黑龙江省教育厅科学技术研究项目（11541053）

摘要

通过有理分式逼近提出了一种高斯滤波器实现方法。由有理分式模型,根据插值逼近方法确定相应系数,得出的有理逼近分式具有较高的逼近精度,与理论高斯滤波器最大幅度偏差为0.88%,截止频率内的幅度偏差小于2‰,是优化的逼近函数。由逼近分式S域左半平面极点建立逼近滤波器,由后向差分变换得出Z域模型,并应用零相移滤波技术得出了零相移数字滤波算法,满足了表面测量中对高斯滤波器实现方法的相位要求。应用这一方法,建立了表面轮廓中线,分离出表面粗糙度数据,整个算法只经一级零相移滤波就能完成,具有较高的计算效率,为表面测量高斯滤波的实现提供了一种新的方法。

关键词: 表面粗糙度测量; 高斯滤波器; 有理逼近; 零相移滤波

中图分类号:TB92 文献标志码:A 文章编号:1671-5497(2014)05-1347-06

Rational approximation implementation approach to determine Gaussian filtering mean line in surface roughness measurement

XU Jing-bo^1,², YUAN Yi-bao³, CUI Xiao-meng^1,², GUO Xin^1,², WANG Sheng^1,²

1.College of Measure-control Technology & Communication Engineering, Harbin University of Science and Technology, Harbin 150080, China

2. The Higher Educational Key Laboratory for Measuring & Control Technology and Instrumentations of Heilongjiang Province, Harbin 150080, China

3. Department of Automation Measurement & Control,Harbin Institute of Technology, Harbin 150001, China

Abstract

Based on rational fraction approximation, an implementation approach for Gaussian filter is presented. The coefficients in the rational fraction are determined by interpolation approximation. The deduced rational fraction is an optimization approximation function with high approximation accuracy. The maximum amplitude deviation from theoretical Gaussian filter is 0.88% in the whole frequency domain, and is less than 2‰ in cutoff frequency. The approximation filter is designed by the poles in the left half plane of S domain, and the corresponding digital filter in Z domain is obtained by backward difference transformation. The corresponding zero-phase-shift digital filtering algorithm is achieved by zero-phase-shift technique that meets the requirements of surface measurement. This method is applied to surface roughness measurement to determine the mean line of surface profile and separate surface roughness. The algorithm has high computation efficiency because it can be implemented by only one stage zero-phase-shift filtering, and provides a new method for surface measurement.

Keyword: surface roughness measurement; Gaussian filter; rational approximation; zero-phase-shift filtering

Show Figures

0 引言

在表面粗糙度测量中,国际标准ISO16610将高斯滤波器列为一种标准滤波器^{[ 1]},用以建立表面轮廓中线,表面粗糙度参数据此定义并计算。然而,对高斯滤波器的设计往往采用逼近的方法。常用的逼近设计方法有基于巴特沃思滤波器的逼近设计方法和基于移动平均滤波器的逼近设计方法。基于巴特沃思滤波器的逼近设计方法是根据中心极限定理,以巴特沃思滤波器作为基本逼近单元,通过多级级联来逼近实现高斯滤波器。同样,基于移动平均滤波器的逼近设计方法是以移动平均滤波器作为基本逼近单元,在中心极限定理作用下,通过多级级联来逼近实现高斯滤波器。在这两种逼近设计方法中,基本逼近单元巴特沃思滤波器和移动平均滤波器的幅频特性与高斯滤波器相差都很大,巴特沃思滤波器通过16级的级联得到的逼近滤波器与高斯滤波器最大幅度偏差达到了1.4%^{[ 2, 3, 4, 5]},而移动平均滤波器通过8级的级联得到的逼近滤波器与高斯滤波器最大幅度偏差达到了1.2%^{[ 2, 3, 4, 5]}。这说明它们主要是依据中心极限定理,通过自身级联来实现高斯滤波器的,中心极限定理在整个逼近滤波器的设计中起到了主要作用。所以巴特沃思滤波器和移动平均滤波器并不是很好的逼近函数,且多级滤波器级联必然增加系统的复杂性,降低数字滤波的计算效率。

本文基于有理逼近设计方法,提出了一种新的高斯滤波器设计方法,它具有较高的逼近精度和计算效率。本文详细论述了该逼近滤波器设计方法,相应的零相移数字滤波算法,以及在表面粗糙度测量中建立滤波中线的应用。

1 高斯滤波器有理逼近设计方法

虽然高斯滤波器在不同的应用领域表达形式各不相同,但对于设计来说,可以将它们归纳为一种形式。在这里,不失一般性,采用频率归一化的表达形式,其幅频特性和幅度平方函数如下:

$\begin{matrix} \begin{matrix} H (jΩ) = e^{- π {(\frac{αΩ}{Ω_{c}})}^{2}} (1) \\ H (jΩ) = e^{- 2 π {(\frac{αΩ}{Ω_{c}})}^{2}} (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} Ω_{c} \end{matrix}$ 为截止频率;由于要求滤波器在截止频率处幅度传输值为0.5,可以求得 $\begin{matrix} α = 0.4697 。 \end{matrix}$

高斯滤波器的幅频特性和幅度平方函数都为实函数,且具有相同的形式,所以对高斯滤波器的逼近设计可以在幅频特性上直接逼近高斯滤波器的幅频特性,如式(1),这实质是函数逼近问题。根据逼近理论^{[ 6]},采用有理分式逼近模型,通过插值逼近方法对高斯滤波器频率特性逼近,有利于后续滤波器的实现,其中有理分式可设为:

$\begin{matrix} P (jΩ) = \frac{a_{0}}{1 + b_{1} {(\frac{Ω}{Ω_{c}})}^{2} + b_{2} {(\frac{Ω}{Ω_{c}})}^{4} + b_{3} {(\frac{Ω}{Ω_{c}})}^{6}} (3) \end{matrix}$

式中: $\begin{matrix} a_{0} 、 b_{1} 、 b_{2} 、 b_{3} \end{matrix}$ 为待定系数。

由于滤波器的特性主要由分母极点决定,分子零点只影响幅度、相位,不改变波形形式,所以这里设分母为多项式形式,而分子只设为一个常数。分母只取偶次幂是由于后续要对有理逼近分式进行分解,由左半平面极点构成逼近滤波器,分母阶次越高,逼近精度也越高,这里6阶已经足够满足要求。

插值点的选择要反映被逼近频率特性曲线在不同频段的特征,并且要使得到有理逼近分式的最大幅度偏差满足一定的精度要求。根据式(1)描述的频率特性,取其一系列特征点,见表1。

表1 插值逼近点 Table 1 Interpolation approximation points

通过数据比较可以看出:选择 $\begin{matrix} Ω_{8}, Ω_{9}, Ω_{10}, Ω_{11} 作为归一化设计的有理逼近插值点, 逼近精度优于常用方法, 完全能够满足设计要求。根据插值逼近原理, 应使 H (jΩ) 和 P (j Ω) \end{matrix}$ 在这些插值点取值相等,即 $\begin{matrix} H (j Ω_{8,9, 10,11}) = P (j Ω_{8,9, 10,11}), \end{matrix}$ 通过矩阵运算可以求得有理逼近分式(3)中的4个待定系数,这样也就建立了有理逼近模型^{[ 7]}:

$\begin{matrix} ψ \cdot θ = Φ (4) \end{matrix}$

式中:

$\begin{matrix} \begin{matrix} ψ = \\ [\begin{matrix} 1 & - H (j Ω_{8}) Ω_{8}^{2} & - H (j Ω_{8}) Ω_{8}^{4} & - H (j Ω_{8}) Ω_{8}^{6} \\ 1 & - H (j Ω_{9}) Ω_{9}^{2} & - H (j Ω_{9}) Ω_{9}^{4} & - H (j Ω_{9}) Ω_{9}^{6} \\ 1 & - H (j Ω_{10}) Ω_{10}^{2} & - H (j Ω_{10}) Ω_{10}^{4} & - H (j Ω_{10}) Ω_{10}^{6} \\ 1 & - H (j Ω_{11}) Ω_{11}^{2} & - H (j Ω_{11}) Ω_{11}^{4} & - H (j Ω_{11}) Ω_{11}^{6} \end{matrix}] = \\ [\begin{matrix} 1 & 0 & 0 & 0 \\ 1 & - 0.2805 & - 0.1010 & - 0.0364 \\ 1 & - 0.5 & - 0.5 & - 0.5 \\ 1 & - 0.2957 & - 1.0673 & - 3.8531 \end{matrix}]; \\ Φ = [\begin{matrix} H (j Ω_{8}) \\ H (j Ω_{9}) \\ H (j Ω_{10}) \\ H (j Ω_{11}) \end{matrix}] = [\begin{matrix} 1 \\ 0.7792 \\ 0.5 \\ 0.0819 \end{matrix}]; θ = [\begin{matrix} a_{0} \\ b_{1} \\ b_{2} \\ b_{3} \end{matrix}] \end{matrix} \end{matrix}$

可以解得:

$\begin{matrix} θ = (ψ^{T} {\cdot ψ)}^{- 1} \cdot ψ^{T} \cdot Φ = [\begin{matrix} 1 \\ 0.7199 \\ 0.1343 \\ 0.1458 \end{matrix}] (5) \end{matrix}$

最后得出有理逼近模型为:

$\begin{matrix} \begin{matrix} P (jΩ) = \\ \frac{1}{1 + 0.7199 {(\frac{Ω}{Ω_{c}})}^{2} + 0.1343 {(\frac{Ω}{Ω_{c}})}^{4} + 0.1458 {(\frac{Ω}{Ω_{c}})}^{6}} (6) \end{matrix} \end{matrix}$

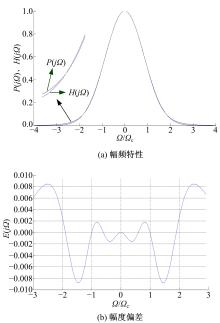高斯滤波器与有理逼近分式幅频特性和幅度偏差曲线如图1所示。可以看出:有理逼近分式以较高的精度逼近了高斯滤波器的幅频特性,整个频域内最大幅度偏差小于1%,在截止频率 $\begin{matrix} Ω_{c} \end{matrix}$ 内最大幅度偏差小于2‰。

	Figure Option View Download New Window
	图1 高斯滤波器与有理逼近分式幅频特性和幅度偏差曲线Fig.1 Amplitude-frequency characteristic and difference of amplitude of Gaussian filter and the rational approximation fraction

在系统初始状态为零的条件下, $\begin{matrix} s = jΩ, \end{matrix}$ 可以得出S域系统函数为:

$\begin{matrix} P (s) = \frac{1}{1 - \frac{0.7199}{Ω_{c}^{2}} s^{2} + \frac{0.1343}{Ω_{c}^{4}} s^{4} - \frac{0.1458}{Ω_{c}^{6}} s^{6}} (7) \end{matrix}$

该系统函数有6个极点,以左半平面极点可构成逼近滤波器:

$\begin{matrix} \begin{matrix} G_{p} (s) = \\ \frac{a}{(s + 1.1285 Ω_{c}) (s^{2} + 2.071 Ω_{c} s + 2.3208 Ω_{c}^{2})} = \\ \frac{2.6190 Ω_{c}^{3}}{(s + 1.1285 Ω_{c}) (s^{2} + 2.071 Ω_{c} s + 2.3208 Ω_{c}^{2})} (8) \end{matrix} \end{matrix}$

由于要求在 $\begin{matrix} Ω = 0 \end{matrix}$ 时滤波器幅频特性为1,故 $\begin{matrix} a = 2.6190 Ω_{c}^{3} 。 \end{matrix}$ 该逼近滤波器的幅度平方函数 $\begin{matrix} {|G_{p} (j Ω)|}^{2} \end{matrix}$ 即为逼近分式,所以通过两级级联可以逼近实现式(1)所描述的高斯滤波器幅频特性,如图2所示。

	Figure Option View Download New Window
	图2 逼近滤波器原型Fig.2 Approximation filter prototype

2 零相移数字滤波算法

第1节论述了如何在幅频特性上逼近高斯滤波器。而对于高斯滤波器的设计,还需在相频特性方面进行逼近设计,高斯滤波器相频特性为零,这就需要设计零相移滤波器。

首先,由得到的模拟高斯逼近滤波器 $\begin{matrix} G_{p} (s) \end{matrix}$ 进行数字滤波器设计,这里根据滤波器S域模型式(8),采用后向差分技术进行设计^{[ 8, 9, 10]}。S域到Z域变换关系式为 $\begin{matrix} s = (1 - z^{- 1}) / T, 其中 T \end{matrix}$ 为采样时间,根据采样定理,可取 $\begin{matrix} T = 1 / 2 Ω_{c} 。 \end{matrix}$ 将变换关系式代入式(8),可得:

$\begin{matrix} \begin{matrix} H (z) = \\ \frac{2.6190}{- 8 z^{- 3} + 36.7980 z^{- 2} - 58.9118 z^{- 1} + 32.7329} (9) \end{matrix} \end{matrix}$

$\begin{matrix} H (z) 即为逼近滤波器 G_{p} (s) \end{matrix}$ 的Z域模型。

其次,进行零相移数字滤波器设计。零相移滤波器是指一个信号序列经过该滤波器滤波后信号序列的相位不发生变化,即该滤波器的相位响应为零。对于实时信号处理的因果系统来说是不可能实现零相移滤波的,而对于一些非实时信号处理的情况,利用当前信号点“前面”和“后面”的信息是可以实现零相移滤波的^{[ 11, 12]}。表面粗糙度测量系统就属于这一情况,它首先将表面测量信号采集存储,然后对存储的数据进行处理,提取中线,计算参数,属于非实时滤波情况,所以在表面粗糙度测量系统中能实现零相移滤波。

零相移数字滤波器原理框图如图3所示,即:

$\begin{matrix} \begin{matrix} \{\begin{matrix} Y (z) = X (z) H (z) H (\frac{1}{z}) \\ Y (e^{jω}) = X (e^{jω}) H (e^{jω}) H (e^{- jω}) = \\ X (e^{jω}) {|H (e^{jω})|}^{2} \end{matrix} \\ (10) \end{matrix} \end{matrix}$

最后,由图3可以得出零相移数字滤波算法,设输入序列为 $\begin{matrix} x (n), 中间序列为 r (n), 输出序列为 y (n), 数据列总点数为 N, \end{matrix}$ 则有:

$\begin{matrix} \{\begin{matrix} r (m) = Ar (m - 1) + Br (m - 2) + \\ Cr (m - 3) + Dx (m) \\ y (N - m) = Ay (N - m + 1) + By (N - \\ m + 2) + Cy (N - m + 3) + Dr (N - m) \end{matrix} \end{matrix}$

式中: $\begin{matrix} A = 1.7998; B = - 1.1242; C = 0.2444; D = 0.08 。 \end{matrix}$

	Figure Option View Download New Window
	图3 零相移数字滤波器原理Fig.3 Principle of zero phase-shift digital filter

对比图2与图3,结合式(10)可以看出,由两级 $\begin{matrix} G_{p} (s) \end{matrix}$ 级联构成的高斯逼近滤波器的幅频特性在一次零相移滤波中就得到了实现,并保证了零相移的特性。在现今普通计算机上(奔腾2.3 GHz CPU、2 GB内存),采用Matlab语言完成该滤波程序只需0.2 s,所以该算法具有很高的计算效率。

3 表面测量中高斯滤波器

在表面粗糙度测量中,国际标准ISO16610已规定使用高斯滤波器作为建立表面轮廓基准线的滤波器,其规定的高斯滤波器的权函数为:

$\begin{matrix} g (t) = \frac{1}{α λ_{c}} e^{- π (t / α λ_{c})^{2}} (11) \end{matrix}$

式中: $\begin{matrix} α = 0.4697; t \end{matrix}$ 为空间域变量; $\begin{matrix} λ_{c} \end{matrix}$ 为截止波长。

对式(11)进行傅里叶变换,可得其频域响应特性:

$\begin{matrix} G (Ω) = \frac{1}{2 π} \int_{-}^{\infty} h (t) e^{- jΩt} dt = e^{- π {(\frac{αΩ}{Ω_{c}})}^{2}} (12) \end{matrix}$

由于空间域波长与频率的对应关系为 $\begin{matrix} Ω = 2 π / λ, \end{matrix}$ 式(12)可以转换成:

$\begin{matrix} H (λ_{c} / λ) = e^{- π {(\frac{α λ_{c}}{λ})}^{2}} (13) \end{matrix}$

至此,可以根据第1、2节所论述的方法设计式(12)所描述的用于表面测量中的高斯滤波器。

4 应用试验

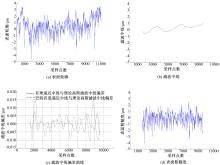
采用马尔表面粗糙度测量仪MarSurf LD120,对一实际工件表面进行测量,选取的截止波长 λ_c=0.8 mm,截止波长内的采样点数为1600,采样间距为0.5 μm。一般地,表面粗糙度参数在5 λ_c内就可进行评定,由于数字滤波器存在边界效应,所以采取扩展采样区间的方法,扩展为7 λ_c的采样区间,滤波后去除受边界效应影响的首尾2 λ_c的数据,由剩下的5 λ_c内数据进行评定。在7 λ_c长度上,总共测得11 200个数据,所测得的表面轮廓数据如图4(a)所示。采用前述方法,变量归一化处理,设计相应的高斯逼近滤波器,得出模拟逼近滤波器为:

$\begin{matrix} \begin{matrix} G_{p} (s) = \\ \frac{2.619}{(\frac{s}{Ω_{c}} + 1.1285) (\frac{s^{2}}{Ω_{c}^{2}} + 2.071 \frac{s}{Ω_{c}} + 2.3208)} (14) \end{matrix} \end{matrix}$

设 $\begin{matrix} N_{c} \end{matrix}$ 为截止波长内采样点数,则有关系式 $\begin{matrix} N_{c} = λ_{c} / T_{s}, T_{s} \end{matrix}$ 为采样间距。利用此关系式,由给定测量条件 $\begin{matrix} N_{c} = 1600, \end{matrix}$ 可推得数字滤波器为:

$\begin{matrix} \begin{matrix} H (z) = \frac{2.619}{N (z)} (15) \\ 式中 : \\ N (z) = - 1.6513 \times 10^{7} z^{- 3} + 4.9746 \times 10^{7} z^{- 2} - \\ 4.9954 \times 10^{7} z^{- 1} + 1.6721 \times 10^{7} \end{matrix} \end{matrix}$

相应的数字滤波算法为:

$\begin{matrix} \{\begin{matrix} r (m) = Ar (m - 1) + Br (m - 2) + \\ Cr (m - 3) + Dx (m) \\ y (N - m) = Ay (N - m + 1) + By (N - \\ m + 2) + Cy (N - m + 3) + Dr (N - m) \end{matrix} \end{matrix}$

式中: $\begin{matrix} A = 2.9875; B = - 2.9751; C = 0.9876; D = 1.5663 \times 10^{- 7} 。 \end{matrix}$

算法只经一次循环就能完成表面轮廓滤波,建立中线,与多级级联逼近滤波器相比,具有较高的计算效率。

由该滤波算法对表面轮廓滤波,得到的高斯滤波中线和表面粗糙度数据分别如图4(b)(d)所示。图4(b)中5 λ_c长度内的数据用作滤波中线输出,由此段分离出的表面粗糙度数据进行参数评定。原始表面轮廓减去滤波中线就可提取出表面粗糙度轮廓,见图4(d),从中可以看出它已经分离出了原始轮廓中的表面波纹度等低频信号。图4(c)为本文方法与理论高斯滤波中线的偏差曲线以及传统方法(8级巴特沃思滤波器逼近方法)得出的滤波中线与理论高斯滤波中线的偏差曲线,图中明显看出本文方法的滤波中线偏差要比传统方法小(即逼近精度高),并且只经过一级零相移滤波就能完成,计算效率明显提高。

	Figure Option View Download New Window
	图4 表面轮廓、滤波中线和表面粗糙度波形Fig.4 Surface profile、filtering meanline and surface roughness profile

5 结束语

本文为高斯滤波器的设计提供了一种新的有理逼近设计方法,该方法具有较高的逼近精度、简捷高效的计算效率,得出的有理逼近分式是高斯函数的优化逼近函数。与传统的基于中心极限定理的逼近方法相比,不需级联,结构简单,在精度和效率两方面都具有优势。在此基础上,应用零相移滤波技术,设计了表面粗糙度测量中所需的高斯滤波器,从设计过程中可以看出该套方法条理清晰、步骤规范,具有推广实用意义。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	ISO16610-2006. Geometrical product specifications (GPS) -Filtration-Part 1: Overview and basic concepts[S]. [本文引用:1]
[2]	Raja J, Muralikrishnan B, Fu Shengyu. Recent advances in separation of roughness, waviness and form[J]. Prec Eng, 2002, 26(2): 222-235. [本文引用:2]
[3]	Yuan Y B, Qiang X F, Song J F, et al. A fast algorithm for determining the Gaussian filtered mean line in surface metrology[J]. Prec Eng, 2000, 24(1): 62-69. [本文引用:2]
[4]	Basu Mitra. Gaussian-based edge-detection methods─a survey[J]. IEEE Transactions on Systems, Man, and Cybernetics─Part C: Applications and Reviews, 2002, 32(3): 252-260. [本文引用:2] [JCR: 2.548]
[5]	Shen Jun, Shen Wei, Castan Serge, et al. Sum-box technique for fast linear filtering[J]. Signal Processing, 2002, 82(8): 1109-1126. [本文引用:2] [JCR: 1.851]
[6]	Cheney Ward, Light Will. 逼近论教程[M]. 北京: 机械工业出版社, 2004. [本文引用:1]
[7]	邱宏安. 随机海浪模型的建立及仿真分析[J]. 系统仿真学报, 2000, 12(3): 226-228. Qiu Hong-an. Establishing and simulation for rand om ocean state model[J]. Journal of System Simulation, 2000, 12(3): 226-228. [本文引用:1] [CJCR: 0.914]
[8]	Young Ian T, van Vliet Lucas J. Recursive implementation of the Gaussian filter[J]. Signal Processing, 1995, 44(2): 139-151. [本文引用:1] [JCR: 1.851]
[9]	陈淑珍, 杨涛. 零相移滤波器的改进及实现方法[J]. 武汉大学学报: 理学版, 2001, 47(3): 373-376. Chen Shu-zhen, Yang Tao. Improvement & realization of the zero-phase filter[J]. Journal of Wuhan University(Nat Sci Ed), 2001, 47(3): 373-376. [本文引用:1]
[10]	乐静, 杨洁, 王建, 等. 基于多层序列图像的三维表面粗糙度检测[J]. 仪器仪表学报, 2010, 31(9): 2036-2041. Le Jing, Yang Jie, Wang Jian, et al. Three-dimensional surface roughness measurement based on sequence multi-images[J]. Chinese Journal of Scientific Instrument, 2010, 31(9): 2036-2041. [本文引用:1] [CJCR: 0.785]
[11]	曹健渭, 卢荣胜, 雷丽巧, 等. 基于散斑纹理变差函数的平磨表面粗糙度测量技术[J]. 仪器仪表学报, 2010, 31(10): 2302-2306. Cao Jian-wei, Lu Rong-sheng, Lei Li-qiao, et al. Grinding surface roughness measurement based on the variogram of speckle pattern texture[J]. Chinese Journal of Scientific Instrument, 2010, 31(10): 2302-2306. [本文引用:1] [CJCR: 0.785]
[12]	尚秀辉, 郭爱煌, 李广宇. 基于零相位数字滤波器的边界问题的分析[J]. 电子测量技术, 2010, 33(4): 25-27. Shang Xiu-hui, Guo Ai-huang, Li Guang-yu. Analysia of the boundary problems based on zero-phase digital filter[J]. Electronic Measurement Technology, 2010, 33(4): 25-27. [本文引用:1] [CJCR: 0.9801]

0.0

... 0 引言在表面粗糙度测量中,国际标准ISO16610将高斯滤波器列为一种标准滤波器^[1],用以建立表面轮廓中线,表面粗糙度参数据此定义并计算 ...

2002

0.0

. 2002, 26(2):null-null

Recent advances in separation of roughness, waviness and form

... 4%^[2,3,4,5],而移动平均滤波器通过8级的级联得到的逼近滤波器与高斯滤波器最大幅度偏差达到了1 ...

... 2%^[2,3,4,5] ...

2000

0.0

. 2000, 24(1):null-null

A fast algorithm for determining the Gaussian filtered mean line in surface metrology

... 4%^[2,3,4,5],而移动平均滤波器通过8级的级联得到的逼近滤波器与高斯滤波器最大幅度偏差达到了1 ...

... 2%^[2,3,4,5] ...

2002

2.548

0.0

... 4%^[2,3,4,5],而移动平均滤波器通过8级的级联得到的逼近滤波器与高斯滤波器最大幅度偏差达到了1 ...

... 2%^[2,3,4,5] ...

2002

1.851

0.0

. 2002, 82(8):null-null

Sum-box technique for fast linear filtering

... 4%^[2,3,4,5],而移动平均滤波器通过8级的级联得到的逼近滤波器与高斯滤波器最大幅度偏差达到了1 ...

... 2%^[2,3,4,5] ...

2004

0.0

... 根据逼近理论^[6],采用有理分式逼近模型,通过插值逼近方法对高斯滤波器频率特性逼近,有利于后续滤波器的实现,其中有理分式可设为: ...

2000

0.0

0.914

. 2000, 12(3):226-228

Establishing and simulation for random ocean state model

给出两种简便、有效的建立随机海浪模型的方法,即能量等分法和有理谱法,并对其进行了仿真与对比分析.它对于进一步研究海上舰船航行控制和直升机海面无线电高度悬停控制有重要意义.

... 根据插值逼近原理,应使H(jΩ)和P(jΩ在这些插值点取值相等,即 H(jΩ8,9,10,11)=P(jΩ8,9,10,11),通过矩阵运算可以求得有理逼近分式(3)中的4个待定系数,这样也就建立了有理逼近模型^[7]: ...

1995

1.851

0.0

. 1995, 44(2):null-null

Recursive implementation of the Gaussian filter

... 首先,由得到的模拟高斯逼近滤波器 Gp(s)进行数字滤波器设计,这里根据滤波器S域模型式(8),采用后向差分技术进行设计^[8,9,10] ...

2001

0.0

. 2001, 47(3):373-376 DOI:10.1023/A:1010293819473

Improvement & realization of the zero-phase filter

1.National Academy of Sciences of Ukraine

A two-stage technique was proposed for cultivating producers of microbial exopolysaccharide ethapolan. The practical value of ethapolan is determined by its rheological properties. The use of a formaldehyde-supplemented medium at the second stage of cultivation improved the rheological properties of ethapolan without reducing its yield. This effect of formaldehyde was due to its binding to the exopolysaccharide, which altered the molecular-weight characteristics of the latter and protected cells against the toxic action of formaldehyde. At all stages of its purification, ethapolan had improved rheological properties, suggesting that it was tightly bound to formaldehyde.

... 首先,由得到的模拟高斯逼近滤波器 Gp(s)进行数字滤波器设计,这里根据滤波器S域模型式(8),采用后向差分技术进行设计^[8,9,10] ...

2010

0.0

0.785

. 2010, 31(9):2036-2041

Three-dimensional surface roughness measurement based on sequence multi-images

提出了一种非接触检测工件表面粗糙度的新方法.利用光学测量显微镜景深小这一特点,将CCD沿金属表面垂直方向等间距拍摄部分聚焦的序列图像,然后采用方差聚焦测度算子确定融合图像中每点所属的高度层次,利用高斯插值方法计算微观物体表面更准确的高度信息,重构了三维微观形貌.同时探讨了三维表面粗糙度参数表征的可行性,通过与二维表面粗糙度参数的对比实验,验证了其正确性和可靠性.该方法对表面粗糙度的在线检测和更完整地表征3D形貌等方面具有参考价值.

... 首先,由得到的模拟高斯逼近滤波器 Gp(s)进行数字滤波器设计,这里根据滤波器S域模型式(8),采用后向差分技术进行设计^[8,9,10] ...

2010

0.0

0.785

. 2010, 31(10):2302-2306

Grinding surface roughness measurement based on the variogram of speckle pattern texture

粗糙表面调制激光散射从而形成散斑.从计算机纹理分析的角度出发,对平面磨削加工金属表面激光散斑图像纹理特征与表面粗糙度之间的关系进行了研究.在研究中采用激光照射平磨表面,用CCD获取散斑纹理图,再对散斑图变化窗口进行变差函数的纹理分析和归一化统计分析,分别提取散斑纹理中的平均值、方差、能量和熵4个特征,表征磨削表面粗糙度.研究和实验结果表明,对于不同大小的窗口,上述4种纹理特征与磨削表面粗糙度Ra之间均存在良好稳定的单调关系.

... 对于实时信号处理的因果系统来说是不可能实现零相移滤波的,而对于一些非实时信号处理的情况,利用当前信号点“前面”和“后面”的信息是可以实现零相移滤波的^[11,12] ...

2010

0.0

0.9801