非对称布局形式的涵道尾桨气动特性

引用本文

刘顺安, 贺兴柱, 陈延礼, 杨璐鸿, 李万林. 非对称布局形式的涵道尾桨气动特性. 吉林大学学报: 工学版, 2014, 44(5): 1353-1359[LIU Shun-an, HE Xing-zhu, CHEN Yan-li, YANG Lu-hong, LI Wan-lin. Aerodynamic characteristics of a ducted tail rotor with asymmetric layout. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1353-1359] 复制到剪切板

Permissions

非对称布局形式的涵道尾桨气动特性

刘顺安, 贺兴柱, 陈延礼, 杨璐鸿, 李万林

吉林大学机械科学与工程学院, 长春 130022

通信作者:陈延礼（1983-）,男,讲师.研究方向:流体传动与控制.E-mail:chenyanli@jlu.edu.cn

作者简介:刘顺安（1951-）,男,教授,博士生导师.研究方向:流体传动与控制.E-mail:lsa@jlu.edu.cn

基金:“863”国家高技术研究发展计划项目(SS2013AA060403)

摘要

针对现行涵道尾桨无法提供升力的缺点,提出一种非对称布局形式的涵道尾桨结构。通过理论分析和数值模拟的方法,对该涵道尾桨的拓扑结构进行气动性能研究,得出涵道尾桨升力、拉力和扭矩分别与飞行速度和开口角有关的结论。对称结构和非对称结构的涵道尾桨气动特性对比结果表明:该非对称布局的涵道尾桨不仅可以产生较大的轴向拉力,对飞行器姿态进行操纵,而且还产生一定的径向力,为飞行器提供额外的升力。总之,该非对称布局的涵道尾桨具有一定的可行性和应用价值。

关键词: 计算流体动力学; 涵道尾桨; 非对称布局; 气动特性

中图分类号:V211 文献标志码:A 文章编号:1671-5497(2014)05-1353-07

Aerodynamic characteristics of a ducted tail rotor with asymmetric layout

LIU Shun-an, HE Xing-zhu, CHEN Yan-li, YANG Lu-hong, LI Wan-lin

College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

Abstract

To overcome the shortcoming of the current ducted tail rotor that is unable to provide lift force, a ducted tail rotor with asymmetric layout was proposed. The aerodynamic performance of the topological structure of the ducted tail rotor was theoretically and numerically studied. The effects of the flight speed and opening angular displacement on the lift force, pull force and moment were obtained respectively. The aerodynamic characteristics of the symmetric and asymmetric ducted tail rotors were compared. It was shown that this ducted tail rotor with asymmetric layout can not only produce axial force to control aircraft attitude, but also produce radial force to provide additional lift force for the aircraft. Therefore, proposed ducted tail rotor with asymmetric layout has certain feasibility and application value.

Keyword: computational fluid dynamics; ducted tail rotor; asymmetric layout; aerodynamic characteristics

Show Figures

0 引言

随着飞行器技术的快速发展,涵道尾桨体现出越来越大的优越性。涵道尾桨与常规尾桨相比,在相同功率下,涵道尾桨不仅直径较小,而且垂尾的气动力可以对桨叶进行卸载,减少飞行器的发动机功率损耗。目前,由于涵道尾桨性能优越,已在世界范围内得到广泛应用,如法国的“小羚羊”涵道尾桨直升机和“海豚”直升机,美国的“科曼奇”直升机和欧洲的“EC135”直升机,以色列的“快骡”涵道无人机等。与此同时,国内外学者对此进行了大量理论研究, Kriebel等^{[ 1]}对涵道螺旋桨的动态稳定性进行了探讨;Anita、Allan等^{[ 2, 3]}分别对涵道风扇系统的性能和轴流特性进行了分析;Dyer^{[ 4]}对一种垂直起降的涵道式飞行器的空气动力学进行了分析;Yaggy、Graf等^{[ 5, 6]}对涵道风扇倾斜状态的空气动力学特性和前飞特性进行了分析;李建波等^{[ 7]}运用实验的方法分析了涵道高度、前倾角、桨距对升阻特性的影响;许和勇等^{[ 8]}运用数值模拟的方法分析出涵道螺旋桨相对于孤立螺旋桨能产生更大的升力,降低功率消耗;上官云信等^{[ 9]}对一种采用新翼型的涵道螺旋桨的气动特性进行了分析;曹义华等^{[ 10]}采用CFD方法对涵道尾桨的气动特性进行了分析。

综上所述,大部分国内外学者的研究工作都是针对对称布局形式的涵道尾桨的气动特性以及稳定性进行的,并没有对非对称布局形式的涵道尾桨进行分析。为此,本文对一种涵道上带有豁口的非对称涵道尾桨进行了研究,并运用数学方法和数值模拟将非对称布局与传统的对称布局的涵道尾桨气动特性进行了对比分析。

1 理论分析

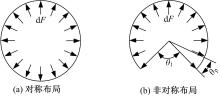
涵道尾桨的周向气动力分布如图1所示。由图1(a)可知,对称布局的涵道尾桨涵道周向的气动力彼此抵消。非对称布局的涵道尾桨如图1(b)所示,由于涵道开设一定角度,致使周向气动力不会完全抵消,即可为飞行器提供额外升力,同时可以有效地限制涡流和回流现象产生。

	Figure Option View Download New Window
	图1 周向气动力分布Fig.1 Circumferential distributions of aerodynamic force

根据涡流理论^{[ 11]},假设条件如下:

(1)螺旋桨为一个前进的桨叶片数无限多的桨盘,理想气流连续地通过桨盘,桨盘拉力分布均匀,桨盘的前、后存在压差,但轴向速度相等。

(2)滑流是均匀的、轴对称的。

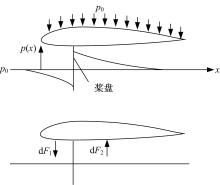
(3)在桨盘上无扭矩,通过桨盘气流无旋转。涵道螺旋桨的轴向气流流动如图2所示,

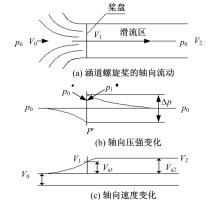	Figure Option '>View Download New Window
'>	图2 涵道螺旋桨的轴向气流流动Fig.2 The ducted propellers' axial flow

根据伯努利方程可得出如下各量的表达式。

桨盘前能量方程为:

$\begin{matrix} p_{0}^{*} = p_{0} + \frac{1}{2} ρ V_{0}^{2} = p' + \frac{1}{2} ρ V_{1}^{2} (1) \end{matrix}$

桨盘后能量方程为:

$\begin{matrix} p_{1}^{*} = p' + Δp + \frac{1}{2} ρ V_{1}^{2} = p_{0} + \frac{1}{2} ρ V_{2}^{2} (2) \end{matrix}$

桨盘前、后的压差为:

$\begin{matrix} \begin{matrix} Δp = p_{1}^{*} - p_{0}^{*} = \\ p_{0} + \frac{1}{2} ρ V_{2}^{2} = p_{0} + \frac{1}{2} ρ V_{0}^{2} = \\ \frac{1}{2} ρ V_{2}^{2} - \frac{1}{2} ρ V_{0}^{2} = \frac{1}{2} ρ (V_{0} + v_{a 2})^{2} - \frac{1}{2} ρ V_{0}^{2} = \\ \frac{1}{2} ρ (2 V_{0} + v_{a 2}) v_{a 2} (3) \end{matrix} \end{matrix}$

螺旋桨拉力 T_P为:

$\begin{matrix} T_{P} = AΔp = ρA (V_{0} + v_{a 2} / 2) v_{a 2} (4) \end{matrix}$

涵道螺旋桨的总拉力 $\begin{matrix} T \end{matrix}$ 为:

$\begin{matrix} T = T_{s} + T_{P} (5) \end{matrix}$

式中: $\begin{matrix} ρ 为来流空气密度; V_{0} 为未受螺旋桨扰动的轴向速度; p_{0} 为未受螺旋桨扰动的轴向压强; p' 为螺旋桨桨盘前的压强; p' + Δp 为螺旋桨桨盘后的压强; v_{a 1} 为桨盘处诱导速度; v_{a 2} 为螺旋桨下游处诱导速度; V_{1} 为桨盘后轴向速度, V_{1} = (V_{0} + v_{a 1}); V_{2} 为滑流区轴向速度, V_{2} = (V_{0} + v_{a 2}); A 为桨盘的面积; T_{s} \end{matrix}$ 为涵道拉力。

将涵道沿弦向进行离化,每段如图3所示,

	Figure Option View Download New Window
	图3 涵道螺旋桨的弦向压力分布Fig.3 Chordwise pressure distribution of the ducted propellers

则每段产生的气动力为:

$\begin{matrix} dF = \int (p (x) - p_{0}) dx (6) \end{matrix}$

桨盘所在位置将涵道沿轴向分成两部分:

$\begin{matrix} \begin{matrix} dF = d F_{1} + d F_{2} = \\ \int_{0}^{h} (p_{1} (x) - p_{0}) dx + \int_{h}^{L} (p_{2} (x) - p_{0}) dx (7) \\ 由图 3 可知 : \\ p_{1} (x) < p_{0}; p_{2} (x) > p_{0} (8) \\ d F_{1} < 0; d F_{2} > 0 (9) \\ dF = d F_{1} + d F_{2} \neq 0 (10) \\ F_{V} = \int_{\frac{θ_{1}}{2}}^{2} \int_{0}^{h} (p_{1} (x) - p_{0}) rcosθdx dθ + \\ \int_{\frac{θ_{1}}{2}}^{2} \int_{h}^{L} (p_{1} (x) - p_{0}) rcosθdx dθ (11) \\ F_{H} = \int_{\frac{θ_{1}}{2}}^{2} \int_{0}^{h} (p_{1} (x) - p_{0}) rsinθdx dθ + \\ \int_{\frac{θ_{1}}{2}}^{2} \int_{h}^{L} (p_{1} (x) - p_{0}) rsinθdx dθ (12) \end{matrix} \end{matrix}$

式中: $\begin{matrix} p_{1} (x) 、 p_{2} (x) 分别为桨盘前、后的轴向压力分布; L 为涵道高度; h 为涵道出口到桨盘距离; θ_{1} 为开口角; d F_{1} 为每微段桨盘前产生的径向力; d F_{2} 为每微段桨盘后产生的径向力; θ 为涵道分布角; F_{V} 为合力的水平分量; F_{H} \end{matrix}$ 为合力的竖直分量。

合力水平分量为零,但是竖直分量不为零。合力竖直分量部分为飞行器提供一部分升力,并且这部分升力随开口角的增大而增大。由于这部分力沿轴向分布方向不同,将会对飞行器产生一个额外力矩。该力矩值与涵道高度有关,当涵道高度变小时,力臂减小,力矩值也将减小。

通过以上分析,可以得出结论:非对称布局的涵道尾桨不但可以产生轴向的拉力,而且可以产生径向的升力。在满足涵道尾桨的功能的同时,既能减轻飞行器重量,又能为飞行器提供额外的升力,降低发动机功率消耗,提高整机效率,但是会对飞行器产生一个附加的力矩。

2 计算模型与数值模拟

2.1 仿真模型

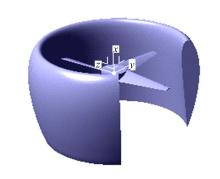
图4为非对称布局的涵道尾桨的计算模型,桨叶采用NACA2412翼型,线性扭转-10°。涵道采用NACA4412翼型旋转产生。非对称布局的涵道尾桨主要参数如下:涵道直径为0.51 m,涵道高度为0.34 m,桨盘距涵道入口距离为0.11 m,涵道开口角为90°,桨叶数为4片。

	Figure Option View Download New Window
	图4 非对称布局的涵道尾桨Fig.4 Asymmetric ducted tail rotor

2.2 网格划分

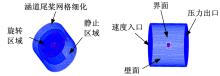
非对称布局的涵道尾桨划分的网格如图5所示。采用非结构网格,为保证计算精度,运用分块处理的方法对螺旋桨和涵道进行网格细化,网格数量为73万左右。其余部分网格数量在42万左右。

	Figure Option View Download New Window
	图5 涵道尾桨网格Fig.5 Grid of ducted tail rotor

2.3 边界条件和求解器参数

边界条件设定如下:计算区域的入口和出口分别采用速度入口和压力出口。螺旋桨设为moving wall,涵道和限制区域均设为station wall,满足无滑移条件。

求解器参数选取如下:分离式、稳态流动、隐式计算、绝对速度公式。参考压力为默认的一个标准大气压,不考虑重力和热交换。为保证鲁棒性和计算精度,选用标准的 $\begin{matrix} k - ε \end{matrix}$ 湍流模型。

采用多重参考系模型(MRF),网格划分包含螺旋桨的旋转区域和涵道的静止区域,对旋转区域进行旋转参数设置(旋转轴、旋转方向、转速、旋转中心位置等)。

3 结果与分析

3.1 流场气动特性对比分析

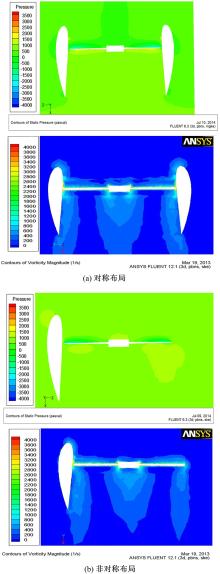
为了研究非对称布局的涵道尾桨的特点,将对称布局和非对称布局的涵道尾桨流场进行对比分析。图6为以轴向对称平面为截面显示的压力和涡量云图。经对比可知,涵道对螺旋桨的桨尖涡有抑制作用,由于非对称布局的涵道尾桨涵道并不完整,在没有涵道保护的部位出现明显桨尖涡,故若要产生与对称布局涵道尾桨相同的拉力,需要更大的功率驱动。由压力云图可知,从涵道入口到桨盘平面,涵道内侧压力小于外侧压力,从桨盘平面到涵道出口,涵道内侧压力略大于外侧压力,在整体上涵道内侧压力应小于外侧压力,存在压力差。

	Figure Option View Download New Window
	图6 涵道尾桨的压力云图和涡量云图Fig.6 Pressure and vortices contour of asymmetric ducted propellers

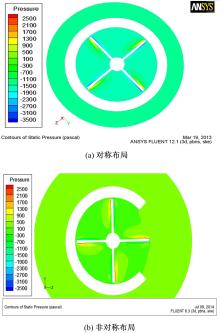图7为对称布局和非对称布局的涵道尾桨以桨盘平面所在截面显示的压力云图。由图可知,桨盘平面涵道内侧压力小于外侧压力,对称布局涵道尾桨布局为圆周对称,由压力差产生的力互相抵消;而非对称布局的涵道尾桨,由于有开口存在,不能完全抵消。对于整个涵道也是如此,由于开口位于上方,故可以产生一个 $\begin{matrix} z \end{matrix}$ 方向的力,为飞行器提供额外的升力。

	Figure Option '>View Download New Window
'>	图7 对称和非对称布局的涵道尾桨桨盘平面压力云图Fig.7 Pressure contour of symmetric and asymmetric ducted propellers' disc flat

为了便于分析,假设非对称布局的涵道尾桨用于推进,定义涵道轴向(即 $\begin{matrix} x 轴方向) 的力为拉力, 涵道径向的力 (即 z 轴方向) 为升力, x 轴扭矩为力矩, y \end{matrix}$ 轴扭矩为俯仰力矩(若涵道尾桨用于平衡反扭矩则为横滚力矩)。来流方向与涵道轴向平行,螺旋桨转速为4000 r/min,螺旋桨的总距为20°,涵道开口位于涵道上方,大小为90°。图8为对称布局与非对称布局的涵道尾桨在不同飞行速度下拉力的变化曲线。由图可知,对称布局与非对称布局的涵道尾桨的拉力相差不大,都随着飞行速度的增加而减小。这是由于随着飞行速度的增加,桨叶的有效迎角减小,故拉力变小。当飞行速度小于6 m/s时,对称布局涵道尾桨产生的拉力比非对称布局的涵道尾桨略小;当飞行速度大于6 m/s时,对称布局涵道尾桨产生的拉力比非对称布局的涵道尾桨略大。

	Figure Option View Download New Window
	图8 拉力随飞行速度的变化曲线Fig.8 Pull force with the change of the speed

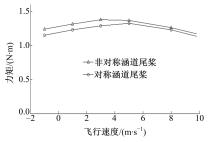
图9为对称布局与非对称布局的涵道尾桨在不同飞行速度下力矩的变化曲线。由图可知,对称布局与非对称布局的涵道尾桨的力矩都随飞行速度的增加先增加而后减小,对称布局涵道尾桨比非对称布局的涵道尾桨所需力矩略小。这是因为非对称布局的涵道尾桨开有豁口,存在气动干扰,造成功率损失,故需要更大的力矩来驱动。

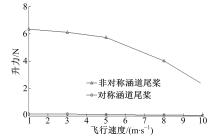
	Figure Option View Download New Window
	图9 力矩随飞行速度的变化曲线Fig.9 Moment with the change of the speed

图10为对称布局与非对称布局的涵道尾桨在不同飞行速度下升力的变化曲线。由图可知,对称布局涵道尾桨产生的升力几乎为零,可以忽略不计。非对称布局的涵道尾桨产生的升力相对较大且随飞行速度的增大而减小。径向升力产生的原因除了螺旋桨旋转使得涵道内部产生负压外,还有涵道自身的作用。即涵道的特殊截面形状,在来流作用下会产生径向升力,径向力的方向与负压产生的升力方向相反,且此径向升力随来流速度的增大而增大。在负压产生的径向升力随来流速度变化不大的情况下,总的径向升力随飞行速度的增大而减小。若将涵道翼型的上下弧线颠倒,使下弧线位于涵道的外侧,上弧线位于涵道的内侧,则涵道产生的径向升力将与负压产生的径向升力同向,会有更大的径向升力产生。

	Figure Option View Download New Window
	图10 升力随飞行速度的变化曲线Fig.10 Lift with the change of the speed

功率增加比(即非对称布局的涵道尾桨相对于对称布局涵道尾桨增加的功率百分比)与升力比(即非对称布局的涵道尾桨产生的升力与对称布局涵道尾桨的拉力的比值)随不同飞行速度下的变化曲线如图11所示。由图可知,非对称布局的涵道尾桨相对于对称布局涵道尾桨功率增加5%,产生相当于25%拉力的额外升力,可以降低功率消耗,提高飞行器效率。

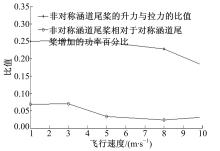	Figure Option View Download New Window
	图11 功率增加比与升力比的变化曲线Fig.11 Ratio of power increased and the ratio of lift with the change of the speed

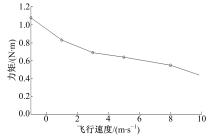
图12为非对称布局的涵道尾桨的俯仰扭矩随飞行速度的变化曲线,由图可知,俯仰力矩随飞行速度的增大而减小,而这个俯仰力矩在对称布局涵道尾桨中并不存在。产生原因已经在前面分析过,其值随飞行速度而减小是因为:随着飞行速度的增大,螺旋桨的诱导速度 $\begin{matrix} v_{a 1} 将减小, 又 v_{a 1} = v_{a 2} / 2, 由式 (3) 可知, Δp \end{matrix}$ 将减小,并且在涵道轴向上分布的不均匀程度将会减弱,体现为俯仰力矩减小。该扭矩的存在将影响到飞行器的操纵性和稳定性,对此可以通过减小涵道高度、增加尾翼的方法来改善。综合图8~图12,可以得出非对称布局的涵道尾桨升力与对称布局的拉力基本相同。通过增加少许功率可以产生较大的额外升力,有利于简化飞行器结构,提高飞行器效率。但是会附加一个俯仰扭矩,为保证飞行器的操纵性和稳定性,可以采用尽量减小涵道高度、增加尾翼的方法来改善附加力矩的影响。

	Figure Option View Download New Window
	图12 俯仰扭矩随飞行速度的变化曲线Fig.12 Pitch moment with the change of the speed

3.2 气动特性随开口角的变化

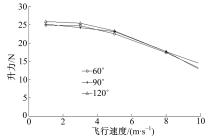
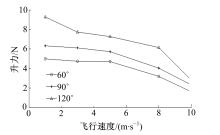
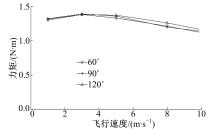
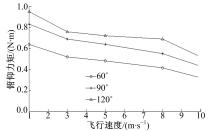
保持转速和总距不变,改变开口角大小,图13~图16分别是不同开口角的非对称布局的涵道尾桨的拉力、升力、扭矩和俯仰力矩随飞行速度的变化曲线。由图13可知,在一定范围内,开口角的大小对非对称布局的涵道尾桨的拉力影响不大,不同开口角下在相同飞行速度时的拉力大体相同。由图14可知,在一定范围内,非对称布局的涵道尾桨的升力随开口角的增大而增大,主要由于开口增大时,不能抵消的气动力增大,因而表现为升力增大。由图15可知,在一定范围内,力矩随开口角的增大略有增大,这是因为随着开口的增大气流扰动变大,因此需要更大的驱动力矩。由图16可知,俯仰力矩随开口角的增大而增大,主要由于随着开口角的增大,在轴向不能被抵消的力变大,导致俯仰力矩增大。

	Figure Option View Download New Window
	图13 不同开口角时的拉力曲线Fig.13 Pull force with various angular displacements

	Figure Option View Download New Window
	图14 不同开口角时的升力曲线Fig.14 Lift with various angular displacements

	Figure Option View Download New Window
	图15 不同开口角时的力矩曲线Fig.15 Moment with various angular displacements

	Figure Option View Download New Window
	图16 不同开口角时的俯仰力矩曲线Fig.16 Pitch moment with various angular displacements

4 结论

(1) 在涵道尾桨开设开口角后,该尾桨的拉力基本不变,升力大幅度增大。

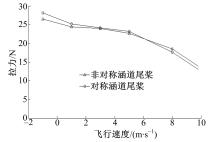
(2) 随着开口角的增大,拉力变化不大,力矩略有增大,而升力增加较大。同时,拉力和升力随飞行速度的增大而减小。

(3) 涵道翼型对升力影响较大,若将涵道翼型的上下弧线颠倒,涵道尾桨的升力将进一步增大。

(4) 非对称布局的涵道尾桨会对飞行器产生一个额外的力矩,力矩的大小随开口角的增大而增大。为减小这个力矩的影响应尽量减小涵道高度。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Kriebel A R, Saeks A H, Nielsen J N. Theoretical investigation of dynamic stability derivatives of ducted propellers[R]. Technical Reports, 1963(1): 63-95. [本文引用:1]
[2]	Anita I Abrego, Robert W. Performance study of a ducted fan system[C]∥Proceeding of American Helicopter Society Aerodynamics, Acoustics, Test and Evaluation Technical Specialists Meeting, San Francisco, CA, 2002. [本文引用:1]
[3]	Allan W R. Axial Flow Fans and Ducts[M]. New York: John Wiley &Sons, Inc, 1983. [本文引用:1]
[4]	Dyer K G. Aerodynamic study of a small ducted VTOL aerial vehicle[D]. Cambridge, UK: Department of Aeronautics and Astronautics, Massachusetts Institute of Technology, 2002. [本文引用:1]
[5]	Yaggy P F, Goodson K W. Aerodynamics of a tilting ducted fan configuration[R]. NASA TND785, 1961. [本文引用:1]
[6]	Graf W, Fleming J, Ng W. Improving ducted fan UAV aerodynamics in forward flight[C]∥46th AIAA Aerospace Science Meeting and Exhibit. Reno: AIAA, 2008: 7-10. [本文引用:1]
[7]	李建波, 高正, 唐正飞, 等. 涵道风扇升力系统的升阻特性实验研究[J]. 南京航空航天大学学报, 2004, 36(2): 164-168. Li Jian-bo, Gao Zheng, Tang Zheng-fei, et al. Experimental investigation on lift and drag of ducted fan system[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2004, 36(2): 164-168. [本文引用:1] [CJCR: 0.3373]
[8]	许和勇, 叶正寅. 涵道螺旋桨与孤立螺旋桨气动特性的数值模拟对比[J]. 航空动力学报, 2011, 26(12): 2821-2825. Xu He-yong, Ye Zheng-yin. Numerical simulation and comparison of aerodynamic characteristics between ducted and isolated propellers[J]. Journal of Aerospace Power, 2011, 26(12): 2821-2825. [本文引用:1] [CJCR: 0.4202]
[9]	上官云信, 钟伯文, 周瑞兴, 等. 采用新翼型的函道螺旋桨气动特性试验与研究[J]. 气动试验与测量控制, 1996, 10(l): 25-29. Shangguan Yun-xin, Zhong Bo-wen, Zhou Rui-xing, et al. Exprimental investigation of Aerodynamic characteristics of shrouded propellers with new aerofoil[J]. Aerodyuamic experiment and measurement & control, 1996, 10(1): 25-29. [本文引用:1]
[10]	曹义华, 陈科. 涵道尾桨气动特性及翼型CFD分析[J]. 航空动力学报, 2004, 19(6): 792-797. Cao Yi-hua, Chen Ke. CFD analysis of aerodynamic characteristics for the ducted tail rotor and its aerofoil[J]. Journal of Aerospace Power, 2004, 19(6): 792-797. [本文引用:1] [CJCR: 0.4202]
[11]	刘沛清. 空气螺旋桨理论及其应用[M]. 北京: 北京航空航天大学出版社, 2006. [本文引用:1]

0.0

... 与此同时,国内外学者对此进行了大量理论研究, Kriebel等^[1]对涵道螺旋桨的动态稳定性进行了探讨 ...

2002

0.0

... Anita、Allan等^[2,3]分别对涵道风扇系统的性能和轴流特性进行了分析 ...

1983

0.0

... Anita、Allan等^[2,3]分别对涵道风扇系统的性能和轴流特性进行了分析 ...

2002

0.0

... Dyer^[4]对一种垂直起降的涵道式飞行器的空气动力学进行了分析 ...

0.0

... Yaggy、Graf等^[5,6]对涵道风扇倾斜状态的空气动力学特性和前飞特性进行了分析 ...

2008

0.0

... Yaggy、Graf等^[5,6]对涵道风扇倾斜状态的空气动力学特性和前飞特性进行了分析 ...

2004

0.0

0.3373

. 2004, 36(2):164-168

Experimental investigation on lift and drag of ducted fan system

近几年出现了许多构形新颖的垂直起降无人飞行器,都以涵道风扇作为升力系统.为了研究涵道风扇系统的气动特性,尤其是在复杂流场中涵道本身的升阻特性,在3.4 m×2.4 m开口风洞中对涵道风扇进行了吹风试验.试验模型由直径1.50 m的可变距风扇系统和外径1.8 m的圆筒状涵道组成.试验状态变量包括涵道高度、吹风速度、涵道前倾角和风扇桨距.试验结果表明:涵道在前飞状态比悬停状态产生更大的升力,但这一优势却被涵道的较大阻力所排斥,因而涵道风扇如果用作升力系统,仅适用于强调悬停和低速飞行的飞行器.

... 李建波等^[7]运用实验的方法分析了涵道高度、前倾角、桨距对升阻特性的影响 ...

2011

0.0

0.4202

... 许和勇等^[8]运用数值模拟的方法分析出涵道螺旋桨相对于孤立螺旋桨能产生更大的升力,降低功率消耗 ...

1996

0.0

... 上官云信等^[9]对一种采用新翼型的涵道螺旋桨的气动特性进行了分析 ...

2004

0.0

0.4202

... 曹义华等^[10]采用CFD方法对涵道尾桨的气动特性进行了分析 ...

2006

0.0

... 根据涡流理论^[11],假设条件如下: ...