作者简介:马尧(1992-),男.研究方向:材料微观性能与3D打印制造.E-mail:myao1992@sina.com
为了有效估计由于粗糙度因素造成纳米压痕测试结果的偏差,对纯铝的纳米压痕进行了有限元仿真研究。利用二维轮廓模型,采用模型轮廓最大高度
To effectively estimate the test deviation of nano-indentation due to surface roughness, a finite element simulation of nano-indentation is carried on pure aluminium. A two dimension model is adopted and the maximum height
纳米压痕技术(Nano-indentation),又称为深度敏感压痕技术,是在特定形状的刚性压头上施加一定的载荷,压入被测样品的表面,同时通过位移传感器采集压入样品的深度信号。纳米压痕测试可以在纳米尺度下测量出材料的力学性能,如硬度、弹性模量、断裂韧性、应变硬化效应以及蠕变行为等[ 1, 2, 3, 4, 5, 6]。在纳米压痕测试中压头压入的深度一般控制在微纳米的尺度下,在实际加载过程中会带来一些误差,特别是在压入深度测量当中存在着偏差。测量误差主要来自测试环境(温度、噪声等)、测试仪器(压头的形状及尖端缺陷、位移和载荷的分辨力、机架柔度等)、被测材料的性质(凹陷、凸起)和材料表面特征(粗糙度等)[ 7, 8]。对于商用的纳米压痕仪来说,载荷和位移分辨力、设备的柔度、噪声等可以看作是固定的,因此,被测材料的性质和表面特征对纳米压痕实验的精度影响尤为重要。Donnelly等[ 9]研究了多孔骨质材料的纳米压痕测试,发现材料表面粗糙度的增加会造成测量数据的分散性的增加,并降低测试精确度。Jiang等[ 10]发现由于材料实际表面粗糙不平,压头的尺寸、压入的深度以及样品的表面形貌都会对纳米压痕结果造成偏差。
有限元仿真方法是分析接触力学的一种有效手段[ 11]。在纳米压痕过程的仿真中,有限元法可以不受实验条件的影响,研究纳米压痕过程中被测试样的应力应变分布,并能够构造单参量变化的材料特性,得出仿真结果进行指导性的试验分析,更好地分析被测材料在压痕实验中的影响因素。Walter等[ 12, 13]分别通过二维和三维有限元模型探究了纳米压痕测试,发现过大的粗糙度对测试硬度和杨氏模量会引入偏差。Chen等[ 14]通过有限元软件ABAQUS模拟了真实表面的粗糙模型,分析了在纳米压痕测试中考虑表面粗糙度的参数识别。本文在前人的基础上,利用有限元软件ABAQUS对塑性材料纯铝的纳米压痕过程进行仿真,研究了不同接触零点对测试结果的影响规律。
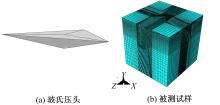
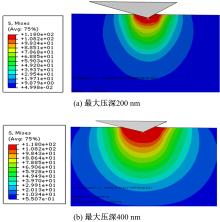
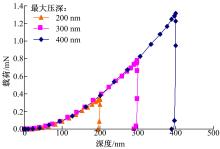
选用纯铝作为仿真被测材料。铝为典型的塑性材料,在室温下,杨氏模量为71 700 MPa,泊松比为0.33,密度为2.7 g/cm3。假设材料为均匀的、各向同性的。根据Bouzakis等[ 15]的研究结果,在其他因素相同的情况下,纳米压痕测试结果与被选压头(维氏压头和玻氏压头)尖端形状无关。本文采用理想形状的玻氏压头和深度控制模式,压深分别为200、300、400 nm。被测试样模型采用棱边长18 μm的正立方体,把压头与试样的接触区域进行了网格细化。将被测试样底面固定作为边界条件,同时给波氏压头施加垂直于试件表面的直线位移。图1(a)为仿真所用的玻氏压头模型,图1(b)为被测试样模型。
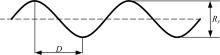
为检测样品表面粗糙度对纳米压痕测试的影响,Jiang等[ 10]采用预制的连续直凹槽来模拟粗糙度的效果,Berke等[ 16]引入正弦函数来模拟样品二维粗糙度形貌,Chen等[ 14]分别采用了单水平的正弦函数和多水平的正弦函数来模拟样品的二维粗糙度形貌,仿真结果证实了以上模型均能在纳米压痕测试中较好地反映真实样品的表面形貌。本文采用轮廓最大高度
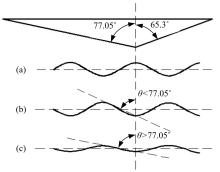
接触零点的确定在纳米压痕测试中是关键的影响因素之一,压头与样品的初始接触位置会对压痕测试结果有着不同的影响[ 14, 15, 16]。在ISO14577[ 17]中推荐两种方法来确定接触零点。方法1:通过拟合函数来确定接触零点(例如二次多项式外推);方法2:通过接触刚度和测试载荷的首次增加量来确定接触零点。本文选用第二种方法。考虑玻氏压头的形状尺寸,玻氏压头棱边与中心线的夹角选为77.05°,引入波谷的垂线与相邻凸面切线之间的夹角
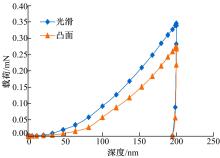
如图6(a)所示,设定压头尖端与粗糙表面波峰接触时即为接触零点。当 D=100 nm, Ry=50 nm, hmax=200 nm时,接触零点在不同表面波峰的深度-载荷曲线图如图7所示。从图中可以看出,接触零点为粗糙表面波峰时,粗糙表面在相同位移下的载荷测试结果比光滑表面的测试结果小。由纳米压痕测试的硬度公式
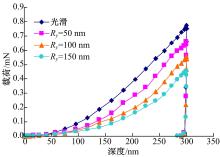
图8为接触零点在不同粗糙度表面波峰仿真得出的深度-载荷曲线图( hmax=300 nm, D=300 nm)。从图中可以看出,相同压入深度下,光滑表面的载荷比粗糙表面的大,粗糙度
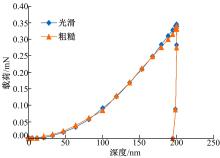
当玻氏压头尖端沿粗糙表面的波谷法线垂直压入,波谷的垂线与相邻凸面切线之间的夹角 θ<77.05°时,如图6(b),压头的尖端还未与粗糙表面底谷接触,其一条棱边就已经与波谷相邻的凸起处发生了接触,载荷开始增加,此时设定压头的棱边与突起接触处为接触零点。当 D=100 nm, Ry=50 nm, hmax=200 nm时,深度-载荷曲线图如图9所示。从图中可以看出,相比光滑表面,此种接触状态下的深度-载荷曲线的偏差较小,两条曲线的吻合性好。
当玻氏压头尖端沿粗糙表面波谷的法线压入,且 θ>77.05°时,设定接触零点在材料表面轮廓的波谷处,如图6(c)所示。由于 θ的大小与
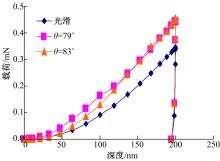
当 hmax=200 nm时,接触零点在不同表面波谷时仿真得出的深度-载荷曲线图如图10所示。从图中可以看出,相比光滑表面的深度-载荷曲线,接触零点在粗糙表面波谷时的最大载荷值比光滑表面的大,说明在此种情况下测得的硬度值偏大。值得注意的是,与光滑表面的曲线相比, θ=79°模型的曲线在深度为20 nm左右时,载荷显现出明显的增加;而 θ=83°模型的曲线在深度为50 nm时载荷才出现明显的增加。推测其原因为:当压头向下移动时,对于 θ=79°的模型,在压深为20 nm时,压头的一条棱边已与波谷相邻的凸起处发生了接触;对于 θ=83°的模型,压深50 nm左右时,压头的一条棱边才与波谷相邻的凸起处发生了接触。
通过对纯铝试样粗糙表面的纳米压痕测试过程进行仿真,发现当模型轮廓最大高度
材料表面粗糙度对纳米压痕的测试结果有显著的影响,越光滑的测试表面越能够精确地反映出材料的真实纳米力学性能。本文通过有限元仿真分析,发现在不同的接触零点,纳米压痕测试结果显示出了不同的效果,仿真结果有助于辨识由于粗糙度因素造成测量参量的偏差,也为合理设计压痕试验提供了指导。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|