目前,大量图像去噪算法的主要研究工作是围绕噪声去除和噪声去除后评估展开。传统的去噪方法根据噪声图像类型不同,分为普通图像、红外图像、医学图像、遥感图像等去噪方法;根据去噪方法所在的信号域,分为空间域去噪和变换域去噪方法;根据噪声类型是否已知,分为已知噪声类型和未知噪声类型去除方法。对已知噪声类型的图像可根据噪声选择空间域或变换域进行噪声去除,如高斯滤波器^{[ 1]}、中值滤波器^{[ 2]}、形态滤波器^{[ 3]}、鲁棒卡尔曼滤波算法(Robust Kalman filter,RKF)^{[ 4]}等。近十多年,噪声去除算法已拓展到偏微分方程(PDE)^{[ 5]}与变分极值最小化^{[ 6]}进行图像自适应滤波,其特点是利用图像是分块光滑的二元函数,以图像边缘为边界,采用分块连续的函数逼近图像中的真实信号,其各向异性扩散能较好地保留边缘和细节。但是由于噪声类型不尽相同,噪声和图像频率常常会发生大范围重叠,或在空间域上图像分块光滑的条件不满足,利用经典滤波技术不可能将噪声频率去除掉,而在空间域也只是使图像本身变得光滑,一部分细节特征信息丢失。使得图像预处理过程中出现了后期分类、检索应用中不希望出现的负面效果,因此设计和选择合适的去噪算法非常关键。更重要的是,现有噪声估计多基于空间白噪声、高斯噪声等已知类型,而实际情况中,噪声的具体信息往往是未知的,即使是噪声协方差矩阵也很难得到。为了解决这类问题,基于噪声的估计方法被提出,一般分为3类:①基于平滑区域方法^{[ 7, 8]},使用有噪图像与去噪后图像的差来估计噪声大小,但纹理和边缘较多的图像易于估计错误。②基于小波估计法^{[ 9, 10]},对图像先进行小波变换,由于噪声多集中在尺度小的高频子带,故将最高频率子带系数认为是噪声,依此估计噪声方差。③基于块的估计法,将噪声图像划分为若干块,并估计每块的噪声,最后用统计方法对整个图像进行估计^{[ 11]},该方法主要依赖于分块区域中的光滑区域,对于纹理、边缘对比度差的图像效果依然很差。

综上所述,对于已知噪声类型的图像去噪研究较为深入,未知噪声图像的去噪主要方法是先估计噪声再去除噪声,但当噪声估计难度过大,直接对图像进行噪声去除也是切实可行的选择方法。

本文探讨如何对夜间远程拍摄获得的实际图像进行有效的降噪处理,以恢复其原始图像的特征信息。但由于该类图像背景与实物的对比度较小,随机噪声干扰大且噪声类型未知,因此给降噪处理带来较大困难。常用的去噪算法是选取背景相对较简单的一个较小区域作为平滑区域进行噪声估计。但其噪声类型估计不准会导致去噪效果降低。文献[12]指出:即使估计时有大量信息可用,估计的概率密度分布函数仍旧可能偏离真实的概率密度分布函数。文献[13]将小波分解的低频子图视为不变,对高频细节进行Meanshift滤波。并提出采用Fourier级数来近似计算高斯函数,提高了去噪声效果。但上述算法对夜间远程拍摄的实际图像的噪声去除效果不明显。为此本文改善了多尺度Meanshift降噪算法,首先对分解的低频子图进行Meanshift平滑;然后对平滑子图进行小波重构,并以Meanshift平滑分析窗为约束完成对未知噪声图像的降噪。

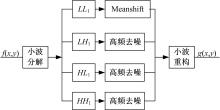
算法采用的是Daubechies正交小波,对原始图像进行一层Mallat塔式分解,分解后得到 LL1、LH1、HL1和 HH1四部分信息。 LL1为原图像的低频子图, LH1、HL1和 HH1分别为图像小波变换的水平高频子图、垂直高频子图和对角线方向高频子图,如图1所示是对一幅红外图像进行Daubechies正交小波变换所得的结果。注意到,在三个高频子图中包含信息较少,只在左上角数字、中间车尾等部分包含有效信息,低频子图则包含了图像的大部分信息,包括图中的噪音信息。这说明在此类图像中,噪音并非存在于高频区域,相比于能发光或反光的物体,噪音的频率反而较低。因此,使用Daubechies正交小波变换后,噪音大部分保留在低频子图中,而在高频子图中更多保留的是边缘信息。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 夜景图的Daubechies正交小波变换结果Fig.1 Orthogonal Daubechies wavelet transform results of night image

本文提出使用Meanshift平滑处理去除残留在低频子图中的噪声分量,将三部分含有高频边缘细节信息通过有某种高频滤波去除噪声,将小波域去噪处理后的4个子图进行小波重构,得到去噪后的重构图像。本文算法框架如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 基于多尺度的Meanshift图像去噪算法框架Fig.2 Denoising framework based on multi-scale Meanshift

本文针对噪声统计特性未知图像提出一种多尺度Meanshift降噪算法,该算法扩大了Meanshift算法的适用范围,解决了未知噪声统计特性的噪声去除问题。具体是通过小波变换抑制高频噪声,利用Meanshift算法的平滑分析窗为约束完成对未知噪声的低频子图进行平滑,重构平滑子图和高频子图。实验结果证明,本文算法具有较强的图像降噪能力。

设 ϕ为尺度函数, φ为小波函数,一幅二维图像的尺度函数为 φ(x,y)以及水平、垂直和对角三个方向的小波函数为 φH(x,y),φV(x,y),φD(x,y),表示如下:

ϕ(x,y)=ϕ(x)ϕ(y)(1)φH(x,y)=φ(x)φ(y)(2)φV(x,y)=φ(x)φ(y)(3)φD(x,y)=φ(x)φ(y)(4)

基于式(1)~(4)的小波和尺度函数的形式,定义可平移与伸缩的基函数如下:

ϕi,m,n(x,y)=2j/2ϕ(2jx-m,2jy-n)=ϕj,m(x)ϕj,n(y)(5)φDi,m,n(x,y)=2j/2φD(2jx-m,2jy-n)=φj,m(x)φj,n(y)(6)φHi,m,n(x,y)=2j/2φH(2jx-m,2jy-n)=φj,m(x)ϕj,n(y)(7)φi,m,nV(x,y)=2j/2φV(2jx-m,2jy-n)=ϕj,m(x)φj,n(y)(8)

根据二元可分离多分辨分析和双尺度方程,可以推导出任意一个二维图像信号 f(x,y)∈L2(R×R)在分辨 2j下进行二维小波变换的Mallat算法,式(5)~(8)又可以表示为:

A2jf=<f(x,y),Φj,n,m(x,y)>=<<f(x,y),Φj,n(x)>,Φj,m(y)>(n,m)∈Z29Dh2jf=<f(x,y),ψhj,n,m(x,y)>=<<f(x,y),Φj,n(x)>,ψj,m(y)>(n,m)∈Z210Dv2jf=<f(x,y),ψvj,n,m(x,y)>=<<f(x,y),ψj,n(x)>,Φj,m(y)>(n,m)∈Z211Dd2jf=<f(x,y),ψdj,n,m(x,y)>=<<f(x,y),ψj,n(x)>,ψj,m(y)>(n,m)∈Z212

再次设给定 d维空间 Rd中的 n个样本点,在某 x点的Meanshift向量为:

Mh(Ajf(x,y))=1k∑(xi,yi)(Ajf(xi,yi)-Ajf(x,y))(13)

式中: Ajf(x,y)为当前样本点灰度值; k表示在这 n个样本点 (xi,yi)中有 k个点落入 Sh区域, Sh为一个半径为 h的高维球区域。

从式(13)可以看出,只要落入 Sh的采样点,无论其距离 (x,y)远近,对 Mh的计算是一样的,但离 (x,y)越近的采样点对估计 Ajf(x,y)周围的统计特性越有效,因此引入单位均匀核函数或单位高斯函数 KH(X),考虑距离影响,并对每个样本都引入一个权重系统^{[ 13]}。为此Meanshift扩展形式为:

Mh(Ajf(x,y))={∑i=1nKHAjf(xi,yi)-Ajf(x,y)hw[Ajf(xi,yi)][Ajf(xi,yi)-Ajf(x,y)]}/{∑i=1nkHAjf(xi,yi)-Ajf(x,y)hw[Ajf(xi,yi)]}(14)

将式(14)的 Ajf(x,y)提到求和号外面来,可得:

Mh(Ajf(x,y))=mh(Ajf(x,y))-Ajf(x,y)(15)式中:mh(Ajf(x,y))=∑i=1nKHAjf(xi,yi)-Ajf(x,y)hw(Ajf(xi,yi))(Ajf(xi,yi))∑i=1nkHAjf(xi,yi)-Ajf(x,y)hw(Ajf(xi,yi))

实验1 为了验证在处理夜间监控图像时只在低频部分进行Meanshift平滑处理的合理性,图3给出了其他两种处理方式(即高频部分平滑和高低频部分均平滑)的对比结果。

由图3可知,只进行低频平滑处理的图像效果最好,能够有效去除夜空、地面上的噪音。为了量化各去噪算法的优劣,本文从性能和效率两个方面对其进行评估。性能方面采用信噪比(Signal to noise ratio,SNR),即图像信号与噪声的方差之比,效率方面统计各个算法的时间开销。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 平滑频段对去噪效果的影响Fig.3 Influence of band smoothing on the performance of de-noising

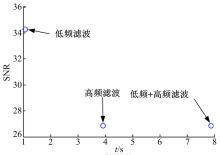
本实验的环境是:DELL t7400+Windows XP+MATLAB(R2009b)。为了降低运行环境对时间开销统计的影响,在图4中所给出的时间均为算法运行5次的平均值。根据图4的横纵坐标可知,数据点越靠近左上角,表明算法的性能和效率越高,反之则越低。从该图可知:①低频滤波算法与其他两种算法比较更接近于左上角,说明该算法优于后两种算法。②低频+高频滤波算法与高频滤波算法比较,性能几乎无提升,但时间开销有所提高。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 各算法在时间与SNR上的比较结果Fig.4 Comparisons on time consumption and SNR

综上所述,三者按从优到劣的排序为:低频滤波算法,高频滤波算法,低频+高频滤波算法。

实验2 图5为本文算法与几种典型去噪算法的比较图。由图可知,本文算法与传统算法相比优势明显,与单一Meanshift去噪方法相比,在纹理区域(如行人的小腿到脚部,地上的小石头)本文算法纹理细节保留较好,这是因为小波变换能把高频细节区分加以保留,Meanshift去除了低频噪声,因此,重构图像比较完整地保留了图像的细节特征。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 几种去噪算法对比图Fig.5 Contrast figure of several denoising algorithm

实验3 图6为本文算法与单一Meanshift算法去噪效果对比的局部截图,观察图6可以发现,对于Lena帽子上的毛织物,与图6(c)相比本文的效果与原图更接近。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 本文算法与单一Meanshift算法去噪效果的局部放大对比图Fig.6 Local contrast figure between the proposed algorithm and single Meanshift algorithm

实验4 图7为本文算法与文献[13]的比较。高频子图保护不变,对低频子图进行Mean shift分析窗平滑,最后合成高频子图与低频滤波后图像,形成去噪声后的图像。可以看出,本文算法获得了较清晰的去噪图像。与未知噪声类型有关,不同噪声类型其噪声分布频率不同,针对实际夜晚拍照图像的噪声,本文算法可以较好地保持图像细节。图8所示是对织物图案的背景平滑及相应去噪后的图像。可以看出,本文对未知噪声图像更具去噪能力。图9为加入椒盐噪声的Brodatz图像及去噪图像,也可看出本文算法对已知噪声图像同样具有较强的去噪能力。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 应用不同多尺度Meanshift图像去噪比较Fig.7 De-noising result based on different multi-scale Meanshift

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 织物图案去噪效果Fig.8 Fabric design denoising result

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 椒盐噪声图像去噪效果Fig.9 Salt & pepper noise image denoising result

本文基于一组在夜间远程拍摄的实际图像展开了复杂背景下的未知噪声类型的图像去噪研究。由于实际图像具有背景与实物对比度小、噪声干扰大的特点,本文进行了大量噪声去除的仿真实验,通过多尺度Meanshift算法有效地去除了实际图像的噪声。同时仿真了中值滤波、均值滤波、维纳滤波等常用滤波去噪,与多尺度Meanshift算法进行实验效果对比,本文算法的信噪比SNR为34.29,优于其他算法,表现出本文的Meanshift去噪算法的优越性,但是也发现高频与低频进行Meanshift平滑存在的差异。如何优化或组合Meanshift去噪算法是下一步研究的方向。同时也可以通过选择平滑区域进行噪声方差估计,再合理推导出未知噪声模型,从而确定Meanshift滤窗的大小是后期的研究工作。