现代互谱估计方法及仿真分析

引用本文

董浩, 迟学芬, 曲良东, 石要武, 赵晓晖, 董超. 现代互谱估计方法及仿真分析. 吉林大学学报: 工学版, 2014, 44(5): 1423-1428[DONG Hao, CHI Xue-fen, QU Liang-dong, SHI Yao-wu, ZHAO Xiao-hui, DONG Chao. Modern cross spectrum estimation method and simulation analysis. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1423-1428] 复制到剪切板

Permissions

现代互谱估计方法及仿真分析

董浩, 迟学芬, 曲良东, 石要武, 赵晓晖, 董超

吉林大学通信工程学院, 长春 130012

通信作者:曲良东（1980-）,男,讲师,博士.研究方向:通信系统,车载网络.E-mail:qld001a@163.com

作者简介:董浩（1981-）,男,讲师,博士.研究方向:通信系统,信号处理,车联网.E-mail:donghao004@163.com

基金:吉林省博士后科研项目（RB201336）

摘要

提出了一种现代互谱估计方法——基于互谱自回归(AR)模型参数估计的SVD算法,相比作者之前提出的基于互谱AR模型参数估计的Levinson算法,本文提出的方法有效地克服了互相关函数r_xy(m)估计误差带来的影响。仿真结果表明:谱估计精度有了很大提高。搭建了测量噪声背景下的仿真平台,对基于该方法的变换域通信系统(TDCS)抗干扰性能进行了仿真研究。结果表明:该方法下TDCS能够有效地抑制测量噪声,在不同干扰下的误码率大大降低,提高了抗干扰能力。

关键词: 通信技术; 变换域通信系统; 自回归模型; 误码率

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2014)05-1423-06

Modern cross spectrum estimation method and simulation analysis

DONG Hao, CHI Xue-fen, QU Liang-dong, SHI Yao-wu, ZHAO Xiao-hui, DONG Chao

College of Communication Engineering, Jilin University, Changchun 130012, China

Abstract

A modern cross spectrum estimation method is proposed, which is the SVD algorithm based on cross-spectrum of the Auto-Regressive (AR) model for parameter estimation. Compared to previously proposed Levinson algorithm based on cross-spectrum of the AR model, the new method of this study can effectively overcome the influence of the estimation error of the cross correlation functionr_xy(m). Simulation results show that the spectrum estimation accuracy of the proposed method is much better. A simulation platform in the measurement noise background is established. The anti-jamming performance of the Transform Domain Communication System (TDCS) based on the proposed method is studied. The results show that the TDCS can effectively suppress the measurement noise, greatly reduce the error rate under different disturbances, and improve the capacity of antidisturbance.

Keyword: communication technology; transform domain communication system; autoregressive model; error rate

Show Figures

0 引言

变换域通信系统(TDCS)由于可以有效抑制通信传输中的干扰问题,近年来针对其抗干扰性能的研究已成为国内外通信系统领域的研究热点^{[ 1, 2]}。信道估计是TDCS的最关键环节,而谱估计法是信道估计的核心方法,谱估计法分为自谱估计法和互谱估计法。自谱估计法分为两种:传统自谱估计法和现代自谱估计法,后者相比前者,大大提高了谱的分辨率,且不受限于数据长度,然而对测量噪声抑制效果很差。在这种背景下,互谱估计法被提出,互谱估计法分为传统互谱估计法和现代互谱估计法,前者虽然能抑制测量噪声,但缺点是谱估计方差较大,谱的分辨率较低。本文对互谱估计理论及方法进行了深入研究,提出一种基于互谱自回归模型的SVD算法的现代互谱估计方法,并对TDCS如何有效抑制测量噪声、降低误码率、提高频谱资源的利用率和通信质量进行了仿真验证。

1 互谱估计理论及方法

1.1 互谱估计问题转化

文献[3]指出,通常为了对信号进行互谱估计运算,首先要将其转化为互谱估计问题,可以通过独立双通道放大器测量方法解决。

图1中,放大器A和B各采用两个相互独立电源 E_CC1和 E_CC2供电,从而所产生的噪声也相互独立。设A和B的放大倍数分别为 $\begin{matrix} k_{1} \end{matrix}$ 和 $\begin{matrix} k_{2}, \end{matrix}$ 则输出信号 $\begin{matrix} x (t) \end{matrix}$ 和 $\begin{matrix} y (t) \end{matrix}$ 分别为:

$\begin{matrix} \begin{matrix} x (t) = k_{1} s_{i} (t) + n_{1} (t) (1) \\ y (t) = k_{2} s_{i} (t) + n_{2} (t) (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} n_{1} (t) \end{matrix}$ 和 $\begin{matrix} n_{2} (t) \end{matrix}$ 为两个相互独立的零均值观测噪声。

根据式(1)(2)能求出 $\begin{matrix} x (t) \end{matrix}$ 和 $\begin{matrix} y (t) \end{matrix}$ 的互相关函数 $\begin{matrix} r_{xy} (τ) \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} r_{xy} (τ) = E \{x (t) y (t + τ)\} = \\ E \{[k_{1} s_{i} (t) + n_{1} (t)] [k_{2} s_{i} (t + τ) + n_{2} (t + τ)]\} = \\ k_{1} k_{2} r_{si} (τ) (3) \end{matrix} \end{matrix}$

显然,这种方法可以抑制噪声,实现对信号的互谱估计。

	Figure Option View Download New Window
	图1 相互独立的双通道互谱估计器原理图Fig.1 Independent cross spectral estimator diagram

1.2 互相关函数、互功率谱的定义

针对互相关函数和互功率谱的定义方式有许多,本文选用最常用的一种定义。

设时间序列 $\begin{matrix} x (n) 、 y (n) \end{matrix}$ 均为各态历经的广义平稳随机过程,且 $\begin{matrix} x (n) 、 y (n) \end{matrix}$ 是平稳相关的,则 $\begin{matrix} x (n) 、 y (n) \end{matrix}$ 之间的互相关函数由下式定义:

$\begin{matrix} \begin{matrix} r_{xy} (m) = E \{x^{*} (n) y (n + m)\} (4) \\ r_{yx} (m) = E \{y^{*} (n) x (n + m)\} (5) \end{matrix} \end{matrix}$

式中:*表示取其共轭^{[ 4]}。

根据维纳-辛钦定理,可直接得到 $\begin{matrix} x (t) 、 y (t) \end{matrix}$ 的互功率谱的定义为:

$\begin{matrix} \begin{matrix} S_{xy} (ω) = \overset{\infty}{\sum_{m = - \infty}} r_{xy} (m) e^{- jωm} (6) \\ S_{yx} (ω) = \overset{\infty}{\sum_{m = - \infty}} r_{yx} (m) e^{- jωm} (7) \end{matrix} \end{matrix}$

1.3 时间序列的线性模型与互功率谱的关系

现代互谱估计方法成立首先需要满足两个条件,即“互谱计算问题”和“互谱分解问题”。前者是指互功率谱可通过两个“联合平稳”随机序列的线性模型直接求得;后者是指通过互功率谱的分解可求得这两个线性模型。

定理1 设时间序列 $\begin{matrix} x (k) \end{matrix}$ 、 $\begin{matrix} y (k) \end{matrix}$ 均为平稳的ARMA过程,且联合平稳,即:

$\begin{matrix} \begin{matrix} x (k) = \frac{B (z^{- 1})}{A (z^{- 1})} ω_{x} (k) (8) \\ y (k) = \frac{D (z^{- 1})}{C (z^{- 1})} ω_{y} (k) (9) \\ 式中 : \\ \frac{B (z^{- 1})}{A (z^{- 1})} = \frac{1 + b_{1} z^{- 1} + \dots + b_{q} z^{- q}}{1 + a_{1} z^{- 1} + \dots + a_{p} z^{- p}} (10) \\ \frac{D (z^{- 1})}{C (z^{- 1})} = \frac{1 + d_{1} z^{- 1} + \dots + d_{m} z^{- m}}{1 + c_{1} z^{- 1} + \dots + c_{n} z^{- n}} (11) \end{matrix} \end{matrix}$

$\begin{matrix} A (z^{- 1}) \end{matrix}$ 和 $\begin{matrix} C (z^{- 1}) \end{matrix}$ 的零点都处于单位圆内; $\begin{matrix} ω_{x} (k) \end{matrix}$ 和 $\begin{matrix} ω_{y} (k) \end{matrix}$ 都为零均值白噪声。

$\begin{matrix} ω_{x} (k) \end{matrix}$ 和 $\begin{matrix} ω_{y} (k) \end{matrix}$ 的互功率谱密度如下:

$\begin{matrix} S_{ω_{x} ω_{y}} (ω) = σ (12) \end{matrix}$

可得 $\begin{matrix} x (k) 、 y (k) \end{matrix}$ 的互功率谱密度为:

$\begin{matrix} S_{xy} (ω) = σ \frac{B (e^{jω}) D (e^{- jω})}{A (e^{jω}) C (e^{- jω})} (13) \end{matrix}$

如果式(9)采用Z变换形式表示,那么可得:

$\begin{matrix} S_{xy} (z) = σ \frac{B (z) D (z^{- 1})}{A (z) C (z^{- 1})} (14) \end{matrix}$

定义1 若互功率谱 $\begin{matrix} S_{xy} (ω) \end{matrix}$ 存在且不为零,且为 $\begin{matrix} e^{jωT} 的有理函数 (T \end{matrix}$ 为采样周期),则称 $\begin{matrix} S_{xy} (ω) \end{matrix}$ 为有理谱。

定理2(互功率谱分解定理) 若联合平稳的两个随机过程的互功率谱 $\begin{matrix} S_{xy} (ω) \end{matrix}$ 具有有理谱形式,且其互相关函数 $\begin{matrix} r_{xy} (m) (m = 0, \pm 1, \dots) \end{matrix}$ 均为实数,则必存在两个零极点均在单位圆内的实系数有理函数:

$\begin{matrix} \begin{matrix} H_{x} (z^{- 1}) = \frac{B (z^{- 1})}{A (z^{- 1})} = \frac{1 + b_{1} z^{- 1} + \dots + b_{r} z^{- r}}{1 + a_{1} z^{- 1} + \dots + a_{s} z^{- s}} (15) \\ 和 \\ H_{y} (z^{- 1}) = \frac{D (z^{- 1})}{C (z^{- 1})} = \frac{1 + d_{1} z^{- 1} + \dots + d_{m} z^{- m}}{1 + c_{1} z^{- 1} + \dots + c_{n} z^{- n}} (16) \\ 满足 : \\ S_{xy} (z) = σ H_{x} (z) H_{y} (z^{- 1}) = σ \frac{B (z) D (z^{- 1})}{A (z) C (z^{- 1})} (17) \end{matrix} \end{matrix}$

式中: $\begin{matrix} σ \end{matrix}$ 为一个标量因子; $\begin{matrix} S_{x y} (z) \end{matrix}$ 为互功率谱 $\begin{matrix} S_{xy} (ω) \end{matrix}$ 的Z变换,该互功率谱分解是唯一的。

2 基于互谱AR模型的SVD算法

2.1 互相关函数的Yule-Walker方程

目前很多“现代”自谱估计法都是在自相关函数的Yule-Walker方程基础上提出的,要构造“现代”互谱估计法,需先创立互相关函数的Yule-Walker方程,具体有下面相关定理。

定理3(互相关函数的Yule-Walker方程) 设时间序列 $\begin{matrix} x (k) 、 y (k) \end{matrix}$ 均为零均值、平稳且联合平稳的实AR过程,即:

$\begin{matrix} \begin{matrix} x (k) = \frac{ω_{x} (k)}{A (z^{- 1})} (18) \\ y (k) = \frac{ω_{y} (k)}{B (z^{- 1})} (19) \\ A (z^{- 1}) = 1 + a_{1} z^{- 1} + \dots + a_{p} z^{- p}; a_{p} \neq 0 (20) \\ B (z^{- 1}) = 1 + b_{1} z^{- 1} + \dots + b_{q} z^{- q}; b_{q} \neq 0 (21) \end{matrix} \end{matrix}$

$\begin{matrix} A (z^{- 1}) \end{matrix}$ 和 $\begin{matrix} B (z^{- 1}) \end{matrix}$ 的根都处于单位圆内; $\begin{matrix} ω_{x} (k) \end{matrix}$ 和 $\begin{matrix} ω_{y} (k) \end{matrix}$ 均为零均值噪声序列,且 $\begin{matrix} E [ω_{x} (k) ω_{y} (k + n)] = σ_{xy} δ (n), δ (n) \end{matrix}$ 为Kronecker Delta函数,则互相关函数序列 $\begin{matrix} r_{xy} (k) 、 r_{yx} (k) (k = 0,1, \dots) \end{matrix}$ 满足下列Yule-Walker方程:

$\begin{matrix} \begin{matrix} [\begin{matrix} r_{xy} (0) & r_{yx} (1) & \dots & r_{yx} (q) \\ r_{xy} (1) & r_{xy} (0) & \dots & r_{yx} (q - 1) \\ ⁞ \\ r_{xy} (q) & r_{xy} (q - 1) & \dots & r_{xy} (0) \end{matrix}] [\begin{matrix} 1 \\ b_{1} \\ ⁞ \\ b_{q} \end{matrix}] = [\begin{matrix} σ_{xy} \\ 0 \\ ⁞ \\ 0 \end{matrix}] (22) \\ 简写为 : \\ R_{xy} B = σ (23) \\ [\begin{matrix} r_{yx} (0) & r_{xy} (1) & \dots & r_{xy} (p) \\ r_{yx} (1) & r_{yx} (0) & \dots & r_{xy} (p - 1) \\ ⁞ \\ r_{yx} (p) & r_{yx} (p - 1) & \dots & r_{yx} (0) \end{matrix}] [\begin{matrix} 1 \\ a_{1} \\ ⁞ \\ a_{p} \end{matrix}] = [\begin{matrix} σ_{xy} \\ 0 \\ ⁞ \\ 0 \end{matrix}] (24) \\ 简写为 : \\ R_{yx} A = σ (25) \end{matrix} \end{matrix}$

2.2 基于互谱AR模型参数估计的SVD算法

设 $\begin{matrix} x (k) 、 y (k) \end{matrix}$ 分别为由式(18)(19)所定义的AR( p)、AR( q)过程,其扩阶Yule-Walker方程分别为:

$\begin{matrix} \begin{matrix} [\begin{matrix} {\hat{r}}_{yx} (0) & {\hat{r}}_{xy} (1) & \dots & {\hat{r}}_{xy} (p_{e} - 1) \\ {\hat{r}}_{yx} (1) & {\hat{r}}_{yx} (0) & \dots & {\hat{r}}_{xy} (p_{e} - 2) \\ ⁞ & ⁞ & ⁞ \\ {\hat{r}}_{yx} (p_{e} - 1) & {\hat{r}}_{yx} (p_{e} - 2) & \dots & {\hat{r}}_{yx} (0) \end{matrix}] \cdot \\ [\begin{matrix} {\hat{a}}_{1} \\ {\hat{a}}_{2} \\ ⁞ \\ {\hat{a}}_{p_{e}} \end{matrix}] = - [\begin{matrix} {\hat{r}}_{yx} (1) \\ {\hat{r}}_{yx} (2) \\ ⁞ \\ {\hat{r}}_{yx} (p_{e}) \end{matrix}] (26) \\ [\begin{matrix} {\hat{r}}_{xy} (0) & {\hat{r}}_{yx} (1) & \dots & {\hat{r}}_{yx} (q_{e} - 1) \\ {\hat{r}}_{xy} (1) & {\hat{r}}_{xy} (0) & \dots & {\hat{r}}_{yx} (q_{e} - 2) \\ ⁞ & ⁞ & ⁞ \\ {\hat{r}}_{xy} (q_{e} - 1) & {\hat{r}}_{xy} (q_{e} - 2) & \dots & {\hat{r}}_{xy} (0) \end{matrix}] \cdot \\ [\begin{matrix} {\hat{b}}_{1} \\ {\hat{b}}_{2} \\ ⁞ \\ {\hat{b}}_{q_{e}} \end{matrix}] = - [\begin{matrix} {\hat{r}}_{xy} (1) \\ {\hat{r}}_{xy} (2) \\ ⁞ \\ {\hat{r}}_{xy} (q_{e}) \end{matrix}] (27) \end{matrix} \end{matrix}$

式中: $\begin{matrix} p_{e} > p; q_{e} > q, \end{matrix}$ 其值不妨取得大些。

式(20)(21)可分别简写为:

$\begin{matrix} \begin{matrix} {\hat{R}}_{yx} A = - {\hat{r}}_{yx} (28) \\ {\hat{R}}_{xy} B = - {\hat{r}}_{xy} (29) \end{matrix} \end{matrix}$

根据矩阵的奇异值分解定理,有:

$\begin{matrix} \begin{matrix} {\hat{R}}_{yx} = UΛ V^{*} (30) \\ 式中 : \\ {\hat{R}}_{yx} {\hat{R}}_{yx}^{*} u_{i} = σ_{i} u_{i} (31) \\ y x^{*} {\hat{R}}_{yx} v_{i} = σ_{i} v_{i} (32) \end{matrix} \end{matrix}$

$\begin{matrix} Λ = diag [σ_{1}, σ_{2}, \dots, σ_{pe}], \end{matrix}$ 且 $\begin{matrix} σ_{i} \end{matrix}$ 按递减顺序排列,即 $\begin{matrix} σ_{1} > σ_{2} > \dots > σ_{pe} 。 \end{matrix}$

将 $\begin{matrix} {\hat{R}}_{yx} 按秩为平 p \end{matrix}$ 的奇异值展开为:

$\begin{matrix} {\hat{R}}_{yx} = \overset{p}{\sum_{i = 1}} σ_{i} u_{i} v_{i}^{*} (33) \end{matrix}$

将 $\begin{matrix} A 用 {U_{i}} \end{matrix}$ 的线性组合表示为:

$\begin{matrix} A = \overset{p}{\sum_{i = 1}} a_{i} v_{i} (34) \end{matrix}$

由式(28)(30)(33),可得:

$\begin{matrix} \begin{matrix} a_{i} = \frac{u_{i}^{*} {\hat{r}}_{yx}}{σ_{i}} (35) \\ 所以有 : \\ A = \overset{p}{\sum_{i = 1}} \frac{u_{i}^{*} {\hat{r}}_{yx}}{σ_{i}} v_{i} (36) \end{matrix} \end{matrix}$

根据矩阵理论,用这种方法求得的 $\begin{matrix} A \end{matrix}$ 为矩阵方程(22)的最小二乘解。

若 $\begin{matrix} {\hat{R}}_{xy} \end{matrix}$ 的奇异值分解式为:

$\begin{matrix} {\hat{R}}_{xy} = \tilde{U} \dot{Λ} {\tilde{V}}^{*} (37) \end{matrix}$

用相同的方法可求得:

$\begin{matrix} B = \overset{q}{\sum_{i = 1}} \frac{{\tilde{u}}_{i}^{*} {\hat{r}}_{xy}}{{\tilde{σ}}_{i}} {\tilde{v}}_{i} (38) \end{matrix}$

实际应用中,通常可取 $\begin{matrix} p_{e} = q_{e}, \end{matrix}$ 这时有:

$\begin{matrix} {\hat{R}}_{xy}^{*} = {\hat{R}}_{yx} (39) \end{matrix}$

因此,只需作一次SVD分解即可,从而大大减少了奇异值分解的计算量。

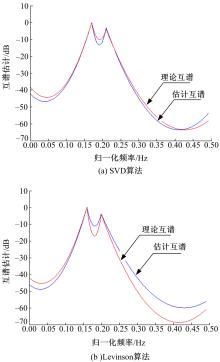
2.3 SVD算法的谱估计性能验证

在之前的研究中^{[ 5]},作者提出的基于互谱AR模型参数估计的Levinson算法忽略了互相关函数 $\begin{matrix} r_{xy} (m) \end{matrix}$ 的估计误差,而本文提出的互谱AR模型参数估计的SVD算法可以有效克服这种估计误差带来的影响,所以SVD算法的谱估计精度要比Levinson算法有很大的提高。

为了验证这一结论,应用和验证Levinson算法谱估计性能采用的相同两个数字仿真模型为:

$\begin{matrix} \begin{matrix} x (k) = 1.58566 x (k - 1) - 2.5573 x (k - 2) + \\ 1.55411 x (k - 3) - 0.9 60596 x (k - 4) + \\ ω (k) + n_{x} (k) \\ y (k) = 1.54515 y (k - 1) - 2.47666 y (k - 2) + \\ 1.48397 y (k - 3) - 0.922368 y (k - 4) + \\ ω (k) + n_{y} (k) \end{matrix} \end{matrix}$

其中,时间序列 $\begin{matrix} x (k) \end{matrix}$ 和 $\begin{matrix} y (k) \end{matrix}$ 的AR模型的极点均在单位圆附近,分别为:

$\begin{matrix} \begin{matrix} [0.99 \exp (\pm j 0.9)] [0.99 \exp (\pm j 0.2)] \\ [0.98 \exp (\pm j 0.95)] [0.98 \exp (\pm j 0.1)] \end{matrix} \end{matrix}$

$\begin{matrix} n_{x} (k) 、 n_{y} (k) \end{matrix}$ 均为测量噪声,分别由方差为1的相互独立的零均值白噪声 $\begin{matrix} ω_{x} (k) \end{matrix}$ 和 $\begin{matrix} ω_{y} (k) \end{matrix}$ 通过两个带通滤波器产生,即:

$\begin{matrix} \begin{matrix} n_{x} (k) = \\ \frac{1}{1 - 1.12117 z^{- 1} + 1.27852 z^{- 2} - 0.549375 z^{- 3} + 0.4076 z^{- 4}} ω_{x} (k) \\ n_{y} (k) = \\ \frac{1}{1 - 1.26135 z^{- 1} + 1.65042 z^{- 2} - 0.80726 z^{- 3} + 0.4096 z^{- 4}} ω_{x} (k) \end{matrix} \end{matrix}$

$\begin{matrix} ω (k) = ω_{x} (k + 4096), ω (k) 、 ω_{x} (k) 、 ω_{y} (k) \end{matrix}$ 是相互独立的,取 $\begin{matrix} x (k) 、 y (k) \end{matrix}$ 的信噪比为0 dB,数据长度为512 ,基于互谱AR模型参数估计的SVD算法和Levinson算法分别得到互谱(幅度谱)估计曲线如图2所示。

	Figure Option View Download New Window
	图2 互谱估计Fig.2 Cross spectral estimation

由图可见,即使在测量噪声和信噪比为0 dB的情况下,本文提出的方法也具有良好的谱估计性能,能有效抑制测量噪声,由于克服了估计误差的影响,其谱估计性能强于互谱Levinson算法。

3 仿真实验

3.1 实验条件

在有测量噪声的背景下,采用数据流仿真和MATLAB软件搭建仿真平台,研究TDCS在不同干扰下的抗干扰能力。

(1)数据源采用随机二进制数。

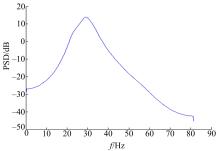
(2)测量噪声 $\begin{matrix} ω_{x} (n) 、 ω_{x} (n) \end{matrix}$ 采用方差为1的白噪声通过一带通滤波器

$\begin{matrix} \begin{matrix} H (z) = \\ \frac{k (1 - 2 z^{- 2} + z^{- 4})}{1 - 1.637 z^{- 1} + 2.237 z^{- 2} - 1.307 z^{- 3} + 0.641 z^{- 4}} \end{matrix} \end{matrix}$ 生成,其功率谱密度曲线如图3所示。

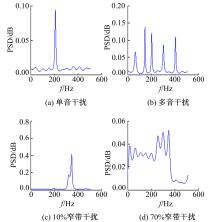
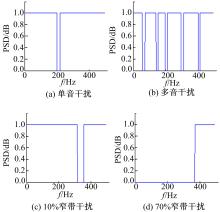
	Figure Option View Download New Window
	图3 测量噪声的功率谱Fig.3 Power spectrum of the measurement noise

(3)干扰分别选用单音干扰、多音干扰、10%窄带干扰和70%窄带干扰。

(4)信噪比 E_b/ N₀=4 dB,干信比 $\begin{matrix} J / E \end{matrix}$ 为0,…,30 dB。

(5)随机相位的范围是:

$\begin{matrix} \begin{matrix} e^{jθ (ω)} = {e^{j θ_{i} (ω)} {|θ}_{i} (ω) \in [0, \frac{2 π}{2^{r}}, \dots, \\ \frac{2 π (2^{r} - 1)}{2^{r}}]} \end{matrix} \end{matrix}$

(6)选用直接序列扩频的抗干扰性能为比较对象。

3.2 实验方法

(1)应用本文提出的方法作为信道谱估计法。

(2)随机序列为9阶的 $\begin{matrix} m \end{matrix}$ 序列,周期是2⁹-1=511。

(3)分别选用双极性调制、二元循环移位键控(BSCK)调制和二元循环翻转移位键控(BCASK)调制方法。

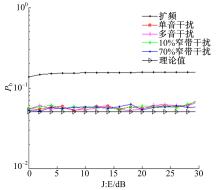
4 仿真结果与比较

由图4可知,在测量噪声背景下,应用本文提出的方法进行谱估计,可以有效抑制测量噪声,谱分辨率较高。由图5可知,针对信道单音干扰、多音干扰、10%窄带干扰和70%窄带干扰,应用幅度谱成型法可以有效抑制这些干扰。

	Figure Option View Download New Window
	图4 在不同干扰下信道的功率谱Fig.4 Channel power spectrum under different interference

	Figure Option View Download New Window
	图5 幅度谱图Fig.5 Amplitude spectrum

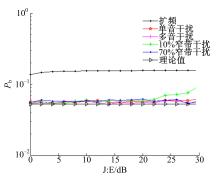
由图6可知,采用双极性调制,TDCS针对多音干扰的抑制效果最好。由图7可知,采用BCSK调制,TDCS针对单音干扰、多音干扰和70%窄带干扰的抑制效果较好,而对10%窄带干扰的抑制效果较差。

	Figure Option View Download New Window
	图6 基于双极性调制的误码率Fig.6 Error rate based on bipolar modulation

	Figure Option View Download New Window
	图7 基于BCSK调制的误码率Fig.7 Error rate based on BCSK modulation

由图8可知,采用BCASK调制,针对不同的干扰,TDCS的误码率都远远低于直接序列扩频通信系统的理论最小误码率。

	Figure Option View Download New Window
	图8 基于BCASK调制的误码率Fig.8 Error rate based on BCASK modulation

5 结束语

对互谱估计理论及方法进行了研究,提出一种现代互谱估计方法。该方法有效克服了互相关函数 $\begin{matrix} r_{xy} (m) \end{matrix}$ 估计误差带来的影响,仿真结果表明其谱估计精度比Levinson算法有了很大提高。在有测量噪声的背景下,应用本文提出的方法对TDCS的抗干扰能力进行了仿真,结果表明:该方法下的TDCS能够有效抑制测量噪声,大大降低了在不同干扰下的误码率,提高了抗干扰能力。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Hu S, Wu G, Xiao Y, et al. Design of low PAPR fundamental modulation waveform for transform domain communication system[J]. Wireless Personal Communications, 2013, 71(3): 2215-2229. [本文引用:1] [JCR: 0.428]
[2]	Hu S, Bi G A, Guan Y L, et al. Spectrally efficient transform domain communication system with quadrature cyclic code shift keying[J]. IET Communications, 2013, 7(4): 382-390. [本文引用:1] [JCR: 0.637]
[3]	赵艳, 张兴周, 缪善林. 基于小波包的变换域通信系统窄带干扰抑制技术[J]. 应用科技, 2007, 34(2): 13-16. Zhao Yan, Zhang Xing-zhou, Miao Shan-lin. The narrowband interference suppression technique of the transform domain communication system based on the wavelet packet[J]. Applied Science and Technology, 2007, 34(2): 13-16. [本文引用:1] [CJCR: 0.3826]
[4]	Han C, Jun W, Shuping G, et al. Detection and performance of the OFDM-based transform domain communication system[C]∥Proceedings of 2006 International Conference on Communications, Circuits and Systems, Beijing, China, 2006: 1332-1336. [本文引用:1]
[5]	董浩, 迟学芬, 曲良东, 等. 基于互谱自回归模型的Levinson算法的变换域通信系统抗干扰性能[J]. 吉林大学学报: 工学版, 2014, 44(3): 812-817. Dong Hao, Chi Xue-fen, Qu Liang-dong, et al. Anti-interference performance of TDCS based on Levinson algorithm of cross pectrum AR model parameter estimation[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(3): 812-817. [本文引用:1] [CJCR: 0.701]

2013

0.428

0.0

. 2013, 71(3):2215-2229 DOI:10.1007/s11277-012-0932-8

Design of low PAPR fundamental modulation waveform for transform domain communication system

1. National Key Laboratory of Science and Technology on Communications, University of Electronic Science and Technology of China (UESTC), Chengdu, Sichuan, China 2. National Mobile Communications Research Laboratory, Southeast University, Nanjing, Jiangsu, China

Abstract To utilize white space spectrum in radio environment, transform domain communication system (TDCS) has been proposed to realize an overlay cognitive radio communication system by using spectrum bin nulling and frequency domain spreading. Being similar to OFDM systems, TDCSs still suffer from the problem of high peak to average power ratio (PAPR) in present of high power amplifier. In this paper, a distortionless PAPR reduction method is proposed for TDCS, namely clipping and phase replacement (CPR). Following this method, the clipping noise-dirty phase vector is replaced by an appropriate replacement, which is selected from the identical phase mapping space to avoid systematic performance degradation. Owing to the high computational complexity from exhaust search, an efficient implementation of CPR method is proposed through the iterative PAPR reduction and phase replacement. Moreover, some considerations for practical applications, such as imperfect spectrum sensing and the number of phase taps, are considered. Analytic and simulation results demonstrate that the distortionless CPR PAPR reduction method is a preferable candidate for TDCSs in both the single-user and multi-user scenarios.

... 0 引言变换域通信系统(TDCS)由于可以有效抑制通信传输中的干扰问题,近年来针对其抗干扰性能的研究已成为国内外通信系统领域的研究热点^[1,2] ...

2013

0.637

0.0

... 0 引言变换域通信系统(TDCS)由于可以有效抑制通信传输中的干扰问题,近年来针对其抗干扰性能的研究已成为国内外通信系统领域的研究热点^[1,2] ...

2007

0.0

0.3826

2006

0.0

... 式中:*表示取其共轭^[4] ...

2014

0.0

0.701

. 2014, 44(3):812-817 DOI:10.13229/j.cnki.jdxbgxb201403037

Anti-interference performance of TDCS based on Levinson algorithm of cross pectrum AR model parameter estimation

College of Communication Engineering, Jilin University, Changchun 130022, China

In this paper, the cross power spectrum estimation theory and method were studied in detail. The Levinson algorithm based on cross-spectrum of the Autoregressive (AR) model parameter estimation was proposed. The good spectral estimation performance of the proposed Levinson algorithm was verified by constructed digital simulation models. Then, the simulation platform was constructed in the measurement of noise background, and the anti-jamming performance of the Transform Domain Communication System (TDCS) based on the proposed Levinson algorithm was investigated. Simulation results show that the proposed method can effectively suppress the measurement noise and the TDCS maintains a strong anti-jamming capability. Thus, the proposed method can improve the communication quality and utilization of the spectrum resources.

对互功率谱估计理论及方法进行了深入研究,提出了基于互谱自回归(AR)模型参数估计的Levinson算法,构建数字仿真模型验证互谱Levinson算法的谱估计性能,结果表明:该方法具有良好的谱估计性能。搭建了测量噪声背景下的仿真平台,对基于互谱AR模型参数估计的Levinson算法的变换域通信系统(TDCS)的抗干扰性能进行了研究,仿真结果表明:该方法下TDCS能够保持较强的抗干扰能力,提高了通信质量和频谱资源的利用率。

... 3 SVD算法的谱估计性能验证在之前的研究中^[5],作者提出的基于互谱AR模型参数估计的Levinson算法忽略了互相关函数 rxy(m)的估计误差,而本文提出的互谱AR模型参数估计的SVD算法可以有效克服这种估计误差带来的影响,所以SVD算法的谱估计精度要比Levinson算法有很大的提高 ...