基于四元数MUSIC算法的声矢量传感器阵列二维波达角估计

引用本文

李新波, 孙海欣, 李晓青, 赵洋, 梁亮, 房小朋. 基于四元数MUSIC算法的声矢量传感器阵列二维波达角估计. 吉林大学学报:工学版, 2014, 44(5): 1453-1459[LI Xin-bo, SUN Hai-xin, LI Xiao-qing, ZHAO Yang, LIANG Liang, FANG Xiao-peng. 2D direction of arrival estimation with acoustic vector sensor array based on quarternions MUSIC algorithm. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1453-1459] 复制到剪切板

Permissions

基于四元数MUSIC算法的声矢量传感器阵列二维波达角估计

李新波¹, 孙海欣², 李晓青¹, 赵洋¹, 梁亮¹, 房小朋¹

1.吉林大学通信工程学院, 长春 130022

2.长春大学电子信息工程学院, 长春 130022

作者简介:李新波(1980-),男,讲师,博士.研究方向:阵列信号处理.E-mail:cinple@126.com

基金:国家自然科学基金项目(51375207); 吉林省青年科研基金项目(20140520064JH)

摘要

利用声矢量传感器导向矢量和四元数之间的相似性,推导并建立了以四元数形式表示的导向矢量,给出了声矢量传感器阵的四元数模型,理论分析了导向矢量与噪声子空间的正交性,在此基础上提出了基于四元数MUSIC空间谱的二维波达角估计方法。仿真实验表明,四元数MUSIC算法的分辨力要优于矢量MUSIC算法,在低信噪比下具有较高的DOA估计精度,验证了四元数的正交性优势,同时本文方法不局限于L线阵和面阵,对其他阵型也具有普遍适用性。

关键词: 信息处理技术; 四元数; 声矢量传感器; MUSIC算法; DOA估计

中图分类号:TN911.7 文献标志码:A 文章编号:1671-5497(2014)05-1453-07

2D direction of arrival estimation with acoustic vector sensor array based on quarternions MUSIC algorithm

LI Xin-bo¹, SUN Hai-xin², LI Xiao-qing¹, ZHAO Yang¹, LIANG Liang¹, FANG Xiao-peng¹

1.College of Communication Engineering, Jilin University, Changchun 130022, China

2.College of Electronics and Information Engineering, Changchun University 130022, China

Abstract

The similarity between the steering vector and quaternion of acoustic vector sensor is utilized to derive and establish the quaternion expressing form of the steering vector, and the quaternion model of the acoustic vector sensor array is proposed. Moreover, the orthogonality of the steering vector and noise subspace is theoretically analyzed. Based on the quaternion Multiple Signal Classification (MUSIC) spatial spectrum, a 2-D Direction of Arrival (DOA) estimation method is proposed. Experiment results show that the resolution of the quaternion MUSIC algorithm is better than that of the vector MUSIC algorithm. In low Signal-to-Noise Ratio (SNR), the quaternion MUSIC algorithm has higher accuracy of DOA estimation. At the same time, this method can be applied not only to the L-shape array and plane array, but also to other array formations.

Keyword: information processing; quaternion; acoustic vector sensor; MUSIC algorithm; DOA estimation

Show Figures

0 引言

近些年,随着声矢量传感器技术的发展及其在军工中潜在的应用前景,水声阵列信号参数估计问题成为了热门研究方向。声矢量传感器能够同步、共点地拾取声场中某点处的声压和振速信息,且各输出分量之间具有正交性。传统的声矢量传感器阵列信号处理方法都是基于声矢量传感器的长矢量模型进行研究的,但长矢量模型没有考虑声矢量传感器输出的各个分量之间的正交关系,而四元数的表达方式能很好地体现这一点。研究表明^{[ 1, 2, 3]},四元数具有较强的正交性约束能力,能更好地描述矢量传感器各通道的正交性结构。用四元数描述声矢量传感器输出的各个分量,增加了正交性约束条件,意味着基于四元数理论的参数估计算法会具有更好的模型误差容错性能。

随着四元数理论在阵列信号处理方面的研究深入,使得基于四元数理论的矢量阵列信号处理方法层出不穷。文献[4]提出的四元数域MVDR算法和改进算法减小了内存需求和计算复杂度,提高了方位估计精度和对相干声源的分辨能力,但是MVDR算法不是超分辨估计算法,受瑞利限的制约;文献[5-6]研究表明,与基于长矢量模型的阵列相比,基于四元数模型的电磁矢量传感器阵列参数估计能获得更高的估计精度和较少的计算量,体现了四元数模型的优势;文献[7]提出了基于四元数的声压振速联合方位估计算法,算法可以在无需平滑处理的情况下分辨相干信号,并且算法的抗各向同性干扰的能力较强;文献[8]提出了基于四元数MUSIC算法的均匀线阵二维波达方向估计算法,减小了运算量并降低了内存需求,但在仿真中导向矢量采用的是常规导向矢量形式。可见,用四元数表示矢量声信息将有助于提高算法的性能。

针对声矢量传感器阵列分析中存在的问题,本文在四元数分析的基础上,开展了基于四元数理论的声矢量传感器阵列信号估计方法研究。将声矢量传感器的声压和三维质点振速信息表示为四元数形式,给出了一种新的导向矢量四元数模型,并在此基础上给出了二维角度的估计方法。

1 四元数理论

1.1 四元数简介

四元数是一种由复数扩维而成的四维超复数,它由一个实部和三个虚部构成,并且三个虚部间满足一定的转换关系。

四元数有以下两种表示形式:

$\begin{matrix} \begin{matrix} q = a + ib + jc + kd (1) \\ a, b, c, d \in R \\ q = α + iβ = a + ib + (c + id) j (2) \end{matrix} \end{matrix}$

虚部间的转换关系为:

$\begin{matrix} \{\begin{matrix} ij = - ji = k \\ jk = - kj = i \\ ki = - ik = j \\ i^{2} = j^{2} = k^{2} = - 1 \end{matrix} (3) \end{matrix}$

四元数的全体称为四元数集,记为 $\begin{matrix} Q 。 \end{matrix}$ 四元数的共轭与模值的定义与复数域中的定义类似。从代数学观点看,四元数是复数域的一种扩展,虽然四元数的运算规则与复数很类似,但是四元数的乘法不满足交换律。

1.2 四元数的正交性

对于四元数的列矢量 $\begin{matrix} w, y \in Q^{N \times 1}, \end{matrix}$ 定义矢量乘积为:

$\begin{matrix} < w, y >_{Q} = y^{H} w (4) \end{matrix}$

如果它们的矢量乘积为零,则就可以认为两个四元数形式的列矢量是正交的。

四元数列矢量 $\begin{matrix} w, y \in Q^{N \times 1} \end{matrix}$ 的复数表示形式为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} w = w_{1} + i w_{2} \\ y = y_{1} + i y_{2} \end{matrix} (5) \\ 记 : \tilde{w} = [\begin{matrix} w_{1} \\ w_{2} \end{matrix}]; \tilde{y} = [\begin{matrix} y_{1} \\ y_{2} \end{matrix}]; \tilde{w}, \tilde{y} \in C (6) \end{matrix} \end{matrix}$

四元数的列矢量 $\begin{matrix} w, y \in Q^{N \times 1} \end{matrix}$ 正交满足^{[ 5, 6]}:

$\begin{matrix} \begin{matrix} (y_{1}^{H} - i y_{2}^{H}) (w_{1} + i w_{2}) = 0 (7) \\ 即 : \\ \{\begin{matrix} y_{1}^{H} w_{1} + y_{2}^{H} w_{2} = 0 \\ y_{1}^{H} w_{2} = y_{2}^{H} w_{1} \end{matrix} (8) \end{matrix} \end{matrix}$

在复数域 $\begin{matrix} C \end{matrix}$ 情况下, $\begin{matrix} \tilde{w}, \tilde{y} \end{matrix}$ 正交满足 $\begin{matrix} < \tilde{w}, \tilde{y} >_{C} = 0, \end{matrix}$ 可得:

$\begin{matrix} y_{1}^{H} w_{1} + y_{2}^{H} w_{2} = 0 (9) \end{matrix}$

对比式(8)(9)可以看出,四元数正交关系和复数正交关系相比具有更多的约束条件,这是四元数正交性优于复数的理论依据。

由表达形式可以看出四元数有更“紧凑”的数据表达形式,一个四元数比复数多包含两个分量,使得它能够在一个运算中包含更多的信息。文献[1,4]就是采用了式(2)形式表示的四元数,由于四元数乘法不满足交换性,将四元数用式(2)的这种复数形式可将四元数转换到复数域中,便于借助成熟的复数理论对四元数理论进行研究。文献[3,5,6,8]采用的是式(1),该形式与声矢量传感器输出分量固有的正交性一致。从四元数正交性的证明可以看出,四元数具有更强的正交性约束条件。

2 声矢量传感器阵列四元数模型

2.1 四元数形式的导向矢量

假设有 $\begin{matrix} N \end{matrix}$ 个远场窄带声源信号入射到 $\begin{matrix} M \end{matrix}$ 个声矢量传感器构成的任意阵列上,声源的入射角为 $\begin{matrix} (θ_{n}, φ_{n}) (n = 1,2, \dots, N), θ_{n} \end{matrix}$ 和 $\begin{matrix} φ_{n} \end{matrix}$ 分别为第 $\begin{matrix} n \end{matrix}$ 个入射声源的方位角和俯仰角,且满足 $\begin{matrix} θ_{n} \in (0,2 π), φ_{n} \in (- π / 2, π / 2) 。 \end{matrix}$ 声源的波长记为 $\begin{matrix} λ_{n} 。第 n \end{matrix}$ 个声源的声压强度表示为 $\begin{matrix} p_{n} (t), \end{matrix}$ 其方向向量 $\begin{matrix} \vec{u_{n}} \end{matrix}$ 记为 $\begin{matrix} (\sin φ_{n} \cos θ_{n}, \sin φ_{n} \sin θ_{n}, \cos φ_{n}), \end{matrix}$ 声源作用在第 $\begin{matrix} m \end{matrix}$ 个声矢量传感器上的质点振速在 $\begin{matrix} X, Y, Z \end{matrix}$ 上的分量分别表示为 $\begin{matrix} v_{xm}^{n} (t), v_{ym}^{n} (t), v_{zm}^{n} (t) \end{matrix}$ 。

设位于坐标原点的阵元为参考阵元,阵元间距为半波长,第 $\begin{matrix} m \end{matrix}$ 个阵元在坐标系中的坐标表示为 $\begin{matrix} (x_{m}, y_{m}, z_{m}) \end{matrix}$ ,第 $\begin{matrix} n \end{matrix}$ 个声源在第 $\begin{matrix} m \end{matrix}$ 个阵元相对于参考阵元的波程差用四元数表示为:

$\begin{matrix} \begin{matrix} Θ_{m}^{n} = \frac{2 π}{λ_{n}} (i x_{m} \sin φ_{n} \cos θ_{n} + j y_{m} \sin φ_{n} \sin θ_{n} + \\ k z_{m} \cos φ_{n}) (10) \end{matrix} \end{matrix}$

相对于参考阵元,第 $\begin{matrix} n \end{matrix}$ 个声源的导向矢量为:

$\begin{matrix} a (Θ^{n}) = {(1, \exp (- Θ_{2}^{n}), \dots, \exp (- Θ_{M}^{n}))}^{T} (11) \end{matrix}$

声矢量传感器阵列的导向矢量矩阵为:

$\begin{matrix} A (Θ) = [a (Θ^{1}), a (Θ^{2}), \dots, a (Θ^{N})] (12) \end{matrix}$

定理若 $\begin{matrix} A (m, n) \end{matrix}$ 表示第 $\begin{matrix} n \end{matrix}$ 个信号在第 $\begin{matrix} m \end{matrix}$ 个阵元上的时延,那么 $\begin{matrix} A (m, n) \in Q; A \in Q^{M \times N} 。 \end{matrix}$

证明由式(10)可知,信号的相位差为:

$\begin{matrix} \begin{matrix} \exp (- Θ_{m}^{n}) = \exp [- \frac{2 π}{λ_{n}} (i x_{m} \sin φ_{n} \cos θ_{n} + \\ j y_{m} \sin φ_{n} \sin θ_{n} + k z_{m} \cos φ_{n})] (13) \\ 令 : α = \frac{2 π x_{m}}{λ_{n}} \sin φ_{n} \cos θ_{n} \\ β = \frac{2 π y_{m}}{λ_{n}} \sin φ_{n} \sin θ_{n} \\ γ = \frac{2 π z_{m}}{λ_{n}} \cos φ_{n} \end{matrix} \end{matrix}$

则式(13)化为:

$\begin{matrix} \exp (- Θ_{m}^{n}) = \exp (- iα) \exp (- jβ) \exp (- kγ) (14) \end{matrix}$

将式(14)按欧拉公式 $\begin{matrix} \exp (iω) = cosω + isinω \end{matrix}$ 展开,可得:

$\begin{matrix} \{\begin{matrix} \exp (- iα) = cosα - isinα \\ \exp (- jβ) = cosβ - jsinβ \\ e xp (- kγ) = cosγ - ksinγ \end{matrix} (15) \end{matrix}$

将式(15)代入式(14),可得:

$\begin{matrix} \begin{matrix} \exp (- Θ_{m}^{n}) = cosαcosβcosγ + sinαsinβsinγ - \\ i (sinαcosβcosγ + cosαsinβsinγ) - \\ j (cosαsinβcosγ + sinαcosβsinγ) + \\ k (sinαsinβcosγ - c o sαcosβsinγ) (16) \end{matrix} \end{matrix}$

式(16)说明 $\begin{matrix} \exp (- Θ_{m}^{n}) \in Q, 即 A (m, n) \in Q, \end{matrix}$ 那么不难分析 $\begin{matrix} A \in Q^{M \times N}, \end{matrix}$ 证毕。

以上分析说明,声矢量传感器的导向矢量可以表述为四元数形式。

2.2 声矢量阵列的四元数模型

声矢量传感器的质点振速与声压的关系为:

$\begin{matrix} \{\begin{matrix} v_{x}^{n} (t) = \sin φ_{n} \cos θ_{n} p_{n} (t) \\ v_{y}^{n} (t) = \sin φ_{n} \sin θ_{n} p_{n} (t) \\ v_{z}^{n} (t) = \cos φ_{n} p_{n} (t) \end{matrix} (17) \end{matrix}$

忽略噪声影响,在 $\begin{matrix} t \end{matrix}$ 时刻第 $\begin{matrix} n \end{matrix}$ 个声源在参考阵元上产生的输出为:

$\begin{matrix} \begin{matrix} q_{1}^{n} (t) = p_{1}^{n} (t) + i v_{x 1}^{n} (t) + j v_{y 1}^{n} (t) + k v_{z 1}^{n} (t) = \\ (1 + isin φ_{n} \cos θ_{n} + jsin φ_{n} \sin θ_{n} + \\ kcos φ_{n}) p_{n} (t) = ρ (θ_{n}, φ_{n}) p_{n} (t) (18) \\ 式中 : ρ (θ_{n}, φ_{n}) = 1 + isin φ_{n} \cos θ_{n} + \\ jsin φ_{n} \sin θ_{n} + kcos φ_{n} (19) \end{matrix} \end{matrix}$

那么,第 $\begin{matrix} n 个声源在第 m \end{matrix}$ 个声矢量传感器上产生的输出用四元数表示为:

$\begin{matrix} \begin{matrix} q_{m}^{n} (t) = q_{m}^{n} (t) + i v_{xm}^{n} (t) + j v_{ym}^{n} (t) + k v_{zm}^{n} (t) = \\ \exp (- Θ_{m}^{n}) ρ (θ_{n}, φ_{n}) p_{n} (t) (20) \end{matrix} \end{matrix}$

于是,声矢量阵列输出为:

$\begin{matrix} \begin{matrix} Z (t) = \overset{N}{\sum_{n = 1}} q^{n} (t) + \overset{N}{\sum_{n = 1}} v_{n} (t) = \\ A (Θ) Q (t) + V (t) (21) \end{matrix} \end{matrix}$

式中: $\begin{matrix} q (t) = {[\begin{matrix} q_{1}^{n} (t) & q_{2}^{n} (t) & \dots & q_{M}^{n} (t) \end{matrix}]}^{T}, A (Θ) 为四元数形式的导向矢量矩阵; N 个入射声源矢量表达矩阵为 Q (t) = [ρ (θ_{1}, φ_{1}) p_{1} (t), ρ (θ_{2}, φ_{2}) p_{2} (t), \dots, ρ (θ_{N}, φ_{N}) p_{N} {(t)]}^{T}; V (t) \end{matrix}$ 为阵列输出的四元数噪声矩阵,各分量为独立同分布的高斯白噪声,且入射声源信号与噪声之间相互独立。

3 基于四元数的MUSIC算法分析

3.1 协方差矩阵

为了便于分析导向矢量与噪声子空间的正交性,定义一种新的导向矢量:

$\begin{matrix} \begin{matrix} b (Θ^{n}) = a (Θ^{n}) ρ (θ_{n}, φ_{n}) (21) \\ ρ (θ_{n}, φ_{n}) = 1 + isin φ_{n} \cos θ_{n} + \\ jsin φ_{n} \sin θ_{n} + kcos φ_{n} (22) \end{matrix} \end{matrix}$

可见, $\begin{matrix} b (Θ^{n}) \end{matrix}$ 为四元数矢量。那么,式(21)可表示为:

$\begin{matrix} \begin{matrix} Z (t) = \overset{N}{\sum_{n = 1}} b (Θ^{n}) p_{n} (t) + \overset{N}{\sum_{n = 1}} v_{n} (t) = \\ B (Θ) P (t) + V (t) (23) \end{matrix} \end{matrix}$

式中: $\begin{matrix} B (Θ) = [b (Θ^{1}), b (Θ^{2}), \dots, b (Θ^{N})] \end{matrix}$ 为一种新的声矢量传感器阵列导向矢量形式; $\begin{matrix} P (t) = {[\begin{matrix} p_{1} (t) & p_{2} (t) & \dots & p_{N} (t) \end{matrix}]}^{T} \end{matrix}$ 为在采样时刻 $\begin{matrix} t \end{matrix}$ 时入射声源信号的声压矩阵,且声压分量间相互统计独立。

阵列数据输出矩阵的协方差矩阵为:

$\begin{matrix} \begin{matrix} R = E [Z (t) Z^{H} (t)] = \\ E {B (Θ) P (t) {[B (Θ) P (t)]}^{H}} + \\ E [V (t) V^{H} (t)] (24) \end{matrix} \end{matrix}$

若定义:

$\begin{matrix} \begin{matrix} Ω = B (Θ) E [P (t) P^{H} (t)] B^{H} (Θ) \\ Γ = E [V (t) V {(t)}^{H}] \end{matrix} \end{matrix}$

式(24)可写为:

$\begin{matrix} R = Ω + Γ (25) \end{matrix}$

式中:矩阵 $\begin{matrix} Γ \end{matrix}$ 为由噪声分量构成的对角矩阵。

3.2 子空间与正交性分析

$\begin{matrix} \begin{matrix} 若定义 : d_{n} = b (Θ^{n}) (26) \\ σ_{n}^{2} = E \{| p_{n} (t) |^{2}} (27) \end{matrix} \end{matrix}$

那么不难分析得到:

$\begin{matrix} Ω = \overset{N}{\sum_{n = 1}} σ_{n}^{2} d_{n} d_{n}^{H} = DΣ D^{H} (28) \end{matrix}$

式中: $\begin{matrix} D = [\begin{matrix} d_{1} & d_{2} & \dots & d_{N} \end{matrix}] \in Q^{M \times N}; Σ = diag (\begin{matrix} σ_{1}^{2} & σ_{2}^{2} & \dots & σ_{N}^{2} \end{matrix}) 。 \end{matrix}$

式(24)变为:

$\begin{matrix} R = DΣ D^{H} + Γ (29) \end{matrix}$

对式(29)中的 $\begin{matrix} R \end{matrix}$ 进行四元数特征分解可得:

$\begin{matrix} R = U D_{λ} U^{H} (30) \end{matrix}$

式中: $\begin{matrix} U = [{\begin{matrix} u_{1} & u_{2} & \dots & u \end{matrix}}_{M}] \in Q^{M \times M} 。 \end{matrix}$

定义两个四元数矩阵 $\begin{matrix} S \in Q^{M \times N}, G = Q^{M \times (M - N)}, 其中, S = [\begin{matrix} u_{1} & u_{2} & \dots & u_{N} \end{matrix}], G = [\begin{matrix} u_{N + 1} & u_{N + 2} & \dots & u_{M} \end{matrix}] 。 \end{matrix}$ 若四元数矩阵 $\begin{matrix} S \end{matrix}$ 为 $\begin{matrix} N \end{matrix}$ 个大特征值对应的特征矢量构成的信号子空间,四元数矩阵 $\begin{matrix} G \end{matrix}$ 为剩余的 $\begin{matrix} M - N \end{matrix}$ 个特征值对应的特征矢量构成的噪声子空间,那么,式(30)可表示为:

$\begin{matrix} R = S D_{S} S^{H} + G D_{G} G^{H} (31) \end{matrix}$

式中: $\begin{matrix} D_{S} 、 D_{G} \end{matrix}$ 分别为信号与噪声子空间对应的特征值所组成的对角矩阵。

式(31)两边乘四元数矩阵 $\begin{matrix} G \end{matrix}$ 可得:

$\begin{matrix} RG = S D_{S} S^{H} G + G D_{G} G^{H} G (32) \end{matrix}$

将式(29)右乘四元数矩阵 $\begin{matrix} G \end{matrix}$ 可得:

$\begin{matrix} RG = DΣ D^{H} G + ΓG (33) \end{matrix}$

比较式(32)和式(33),且 $\begin{matrix} S^{H} G = 0, \end{matrix}$ 得:

$\begin{matrix} \begin{matrix} D^{H} G = 0 (34) \\ 即 : b^{H} (Θ_{n}) G = 0 (35) \end{matrix} \end{matrix}$

式(35)表明,本文定义的导向矢量(21)与噪声子空间 $\begin{matrix} G \end{matrix}$ 正交。

3.3 MUSIC空间谱

将式(35)右乘 $\begin{matrix} (b^{H} (Θ_{n} {) G)}^{H}, \end{matrix}$ 可得:

$\begin{matrix} b^{H} (Θ_{n}) G G^{H} b (Θ_{n}) = 0 (36) \end{matrix}$

定义噪声投影矩阵 $\begin{matrix} Π_{N} = G G^{H} \in Q^{M \times M}, \end{matrix}$ 则四元数MUSIC算法的谱估计公式为^{[ 9]}:

$\begin{matrix} P_{qmusic} = \frac{1}{b^{H} (Θ_{n}) Π_{N} b (Θ_{n})} (37) \end{matrix}$

实际中,阵列接收的数据长度有限,阵列数据的协方差矩阵用下式估计:

$\begin{matrix} \hat{R} = \frac{1}{L} \overset{L}{\sum_{i = 1}} Z Z^{H} (38) \end{matrix}$

式中: $\begin{matrix} L \end{matrix}$ 为快拍数。

对 $\begin{matrix} \hat{R} \end{matrix}$ 进行特征值分解得到噪声子空间 $\begin{matrix} {\hat{U}}_{2} 。 \end{matrix}$ 考虑到噪声的影响, $\begin{matrix} B (Θ) \end{matrix}$ 与 $\begin{matrix} {\hat{U}}_{2} \end{matrix}$ 不完全正交,即式(36)不完全为零。

文献[8]研究表明,基于四元数模型的算法比基于长矢量模型的算法的计算量明显降低,并对其计算量和存储空间进行了详细说明,所以本文未深入探讨。

4 仿真实验

4.1 基于L型声矢量传感器阵列的仿真实验

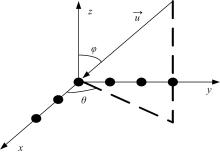
L型阵列如图1所示。各阵元在坐标轴上等间距排列。实验中,阵列由9个阵元组成,阵元间距取为波长的一半,传播介质为水,背景噪声为零均值的高斯白噪声,快拍数为1024。

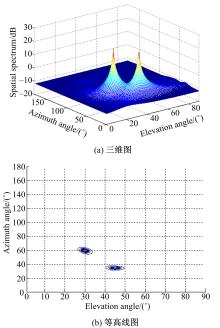
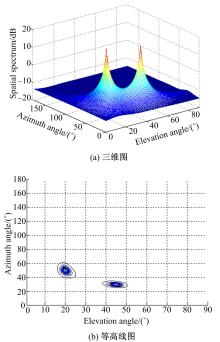
	Figure Option View Download New Window
	图1 L型声矢量传感器阵列分布Fig.1 distribution of acoustic vector sensor array

实验1 四元数MUSIC算法对多声源DOA估计实验。两个待测声源信号的入射角分别为(30°,60°)和(45°,35°),两个声源的载波频率分别为: $\begin{matrix} f_{1} = 200 Hz, f_{2} = 250 Hz 。 \end{matrix}$ 信噪比SNR为5 dB。仿真结果如图2、图3所示。可见,四元数MUSIC算法仿真图形的峰值与分辨率的仿真结果都好于传统的V-MUSIC算法^{[ 1, 10]}。文中提出的四元数MUSIC算法能够成功分辨出两个入射声源信号的入射角度。

	Figure Option View Download New Window
	图2 双声源V-MUSIC算法的DOA实验Fig.2 V-MUSIC algorithm DOA experiment for double sources

	Figure Option View Download New Window
	图3 双声源Q-MUSIC算法的DOA实验Fig.3 Q-MUSIC algorithm DOA experiment for double sources

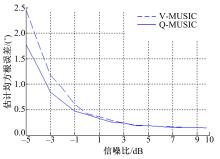
实验2 四元数MUSIC算法在不同信噪比条件下对入射声源信号DOA估计性能实验。信噪比SNR从-5 dB到10 dB变化,变化间隔为1 dB。

使用四元数MUSIC算法以及矢量MUSIC算法在每个信噪比下分别进行100次独立的蒙特卡洛实验。采用联合均方根误差作为评判准则,其中联合均方根误差公式如下:

$\begin{matrix} RMSE = \sqrt[]{E [{(\hat{θ} - θ)}^{2} + {(\hat{φ} - φ)}^{2}]} (39) \end{matrix}$

从图4可以看出,在信噪比小于3 dB的情况下四元数MUSIC算法的估计误差小于矢量MUSIC算法的估计误差,在低信噪比情况下四元数正交性带来了优势。

	Figure Option View Download New Window
	图4 均方根误差估计Fig.4 RMSE of DOA versus SNR

4.2 基于面阵的声矢量传感器阵列的仿真实验

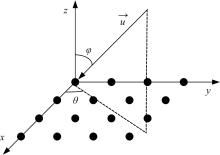
面阵的阵元分布如图5所示,各阵元在坐标轴上等间距排列。实验中,阵列由16个阵元组成,阵元间距取为波长的一半,传播介质为水,背景噪声为零均值的高斯白噪声,快拍数为1024。此处为了简便,只给出双声源的仿真实验。

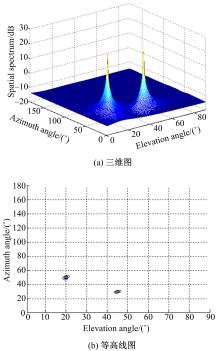
	Figure Option View Download New Window
	图5 面阵中阵元分布Fig.5 array element distribution in Plane array

实验3 四元数MUSIC算法对多声源DOA估计实验。两个待测声源信号的入射角分别为(20°,50°)和(45°,30°),其余条件与L型中的实验条件相同。仿真结果见图6和图7。

	Figure Option View Download New Window
	图6 双声源V-MUSIC算法的DOA实验Fig.6 V-MUSIC algorithm DOA experiment for double sources

	Figure Option View Download New Window
	图7 双声源Q-MUSIC算法的DOA实验Fig.7 Q-MUSIC algorithm DOA experiment for double sources

从结果可以看出,四元数MUSIC算法仿真图形的峰值与分辨力的仿真结果都好于V-MUSIC算法。

实验4 基于平面声矢量传感器阵列的四元数MUSIC算法在不同信噪比条件下对声源信号DOA估计的性能分析实验。实验条件及方法与L型阵列仿真实验相同。仿真结果如图8所示。

从图8可以看出,在信噪比较小的情况下四元数MUSIC算法的估计误差小于矢量MUSIC算法的估计误差。

	Figure Option View Download New Window
	图8 均方根误差估计Fig.8 RMSE of DOA versus SNR

5 结束语

研究了基于声矢量传感器阵列的四元数MUSIC算法,分析了导向矢量的四元数模型,并在此基础上定义了一种新的导向矢量,分析了在此情况下MUSIC空间谱的正交性。算法利用四元数的数据表达形式和较强的正交性约束能力,获得了较之于常规MUSIC算法较好的DOA估计效果。仿真结果表明:本文提出的算法在低信噪比的情况下对声源信号的DOA估计性能优于传统的MUSIC算法,并且四元数MUSIC算法的分辨力要优于矢量MUSIC算法,实验验证了四元数的正交性强于复数的理论。此外,本论文所提出的算法不局限于L阵和平面阵,还可以拓展到圆阵、双平行线阵等其他阵型。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	何光进, 程锦房, 张炜. 基于四元数的声压振速联合方位估计算法[J]. 武汉理工大学学报, 2012, 36(4): 712-716. He Guang-jin, Cheng Jin-fang, Zhang Wei. Sound pressure and velocity joint estimation algorithm based on quaternion[J]. Journal of Wuhan University of Technology, 2012, 36(4): 712-716. [本文引用:2] [CJCR: 0.529]
[2]	刘兆霆, 阮谢永. 色噪声背景下基于声矢量阵列孔径扩展的相干目标波达方向估计[J]. 兵工学报, 2011, 32(3): 257-263. Liu Zhao-ting, Ruan Xie-yong. Direction of arrival estimation of coherent target based on aperture extension of acoustic vector array under colored noise background[J]. Journal of Armaments Factories, 2011, 32(3) : 257-263. [本文引用:1]
[3]	Sebastian Miron, Nicolas Le Bihan. High resolution vector-sensor array processing using quarternions[C]∥IEEE Workshop Statistical Signal Processing, Bordeaux, 2005. [本文引用:1]
[4]	何光进, 程锦房, 刘毅. 声矢量阵方位估计算法及其改进[J]. 计算机仿真, 2012, 29(11): 162-165. He Guang-jin, Cheng Jin-fang, Liu Yi. Azimuth estimation algorithm and its improvement of acoustic vector array[J]. Computer Simulation, 2012, 29(11) : 162-165. [本文引用:1] [CJCR: 0.5628]
[5]	Miron Sebastian, Bihan Nicolas Le. Quarternion MUSIC of vector sensor array processing[J]. IEEE Transactions on Signal Processing, 2006, 54(4): 1218-1229. [本文引用:1] [JCR: 2.813]
[6]	Bihan Nicolas Le, Miron Sebastian, Mars Jerome I. MUSIC algorithm for vector sensors array using biquaternions[J]. IEEE Transactions on Signal Processing, 2007, 55(9): 4523-4533. [本文引用:1] [JCR: 2.813]
[7]	刘靖, 崔晗, 陈芳炯. 一种基于声矢量传感器阵列的二维来波方向和阵列增益联合估计算法[J]. 科学技术与工程, 2009, 9(9): 2332-2335. Liu Jing, Cui Han, Chen Fang-jiong. 2-D direction of arrival and array gain joint estimation algorithm based on acoustic vector sensor array[J]. Science, Technology and Engineering, 2009, 9(9) : 2332-2335. [本文引用:1]
[8]	Wang You-hua, Zhang Jian-qiu, Hu Bo, et al. Hypercomplex model of acoustic vector sensor array with its application for the high resolution two dimensional direction of arrival estimation[C]∥IEEE International Instrumentation and Measurement Technology Conference, Canada, 2008. [本文引用:1]
[9]	张揽月, 杨徳森. 基于MUSIC算法的矢量水听器阵源方位估计[J]. 哈尔滨工程大学学报, 2004, 25(1): 30-33. Zhang Lan-yue, Yang De-sen. Azimuth estimation of vector hydrophone array based on MUSIC algorithm[J]. Journal of Harbin Engineering University, 2004, 25(1): 30-33. [本文引用:1] [CJCR: 0.464]