作者简介:康晓涛(1957-),女,教授.研究方向:信号处理.E-mail:kxt511@sohu.com
在高斯色噪声背景下,提出了高阶累积量最小范数算法,实现了均匀线阵双基MIMO雷达的波离方向和波达方向的联合估计。最小范数算法利用双基MIMO雷达的联合导向矢量矩阵与噪声子空间正交,用噪声子空间的全部噪声奇异矢量构成最小范数矢量,相比MUSIC算法计算量小。仿真结果也表明在低信噪比时,最小范数算法的估计性能较好。
A minimum norm algorithm is proposed to implement the joint estimation of direction of departure and direction of arrive under the background of Gaussian color noise. The minimum norm algorithm is based on the higher order cumulant aimed at the Uniform Linear Array (ULA) double-based MIMO radar. By utilizing the orthogonality between joint steering vector matrix and the noise subspace, a minimum norm vector is obtained from the all noise singular vectors. So the calculation complexity is reduced and the parameter estimation accuracy is improved. The simulation results show that the performance of the proposed minimum norm algorithm is better when SNR is low.
随着MIMO技术理论的逐渐成熟以及先进雷达技术的不断涌现,MIMO雷达应运而生。特别地,双基地MIMO雷达接收和发射阵列分开部署,进行目标探测定位,因其具有灵活性、生存性和隐蔽性而受到了越来越多的关注[ 1]。Yan等[ 2]给出了Capon算法在MIMO雷达中的应用,进行空间谱估计,但其计算量太大。Chen等[ 3]给出了ESPRIT方法在MIMO雷达中的应用,但要确定目标位置,必须参数配对。用经典MUSIC算法实现MIMO雷达的DOA和DOD的联合估计[ 4],在进行谱峰搜索时,计算量较大,角度分辨率较低。
目前,高阶统计量的研究主要集中于三阶和四阶的累积量及其相应的高阶谱方面。高阶统计量具有盲高斯性、相位可检测性和更多的高阶信息等特点。在阵列测向中,利用高阶累积量的盲高斯性可以抑制空间色高斯噪声。洪振清等[ 5]利用四阶累积量有效地扩展阵列孔径,并且适用于任意加性高斯噪声环境。梁浩等[ 6]利用MIMO雷达的接收数据计算出四阶累积量,构造出累积量切片矩阵,具有自动抑制加性高斯噪声和任意高斯色噪声的能力。徐定杰等[ 7]从累积量的基本定义出发,构造出四阶累积量矩阵,通过特征值分解有效地分离出噪声子空间抑制高斯色噪声的影响,提高目标的角度估计性能。
本文利用四阶累积量将噪声子空间的全部噪声奇异矢量构成最小范数矢量,解决了MUSIC算法因谱峰搜索计算量大的问题,且提高了参数估计的精度。
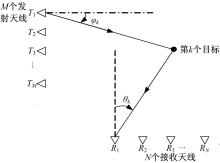
双基MIMO雷达由
设有
式中:发射阵列方向矩阵为
双基MIMO雷达由
式中:
当发射端发射
式中:
定义矩阵
式中:cum{·}表示累积量运算符;“*”表示共轭。
将式(4)代入式(5),可得:
在式(6)中,由于
式中:
将式(8)代入式(7),可得:
式中:
假设存在列向量
对矩阵
式中:
所有奇异矢量构成一个正交集,且有:
矩阵
将奇异矢量矩阵
同样,将奇异矢量矩阵
由式(11)可得:
根据前面结论,
由上述结论可知,若
由上述讨论可知,满足条件的列向量
令
由式(15)
特征矢量
则均匀线阵MIMO雷达联合DOA和DOD估计可从下式得到:
式中:
对基于高阶累积量最小范数算法的性能进行分析,并与MUSIC算法的性能进行比较。参数如下:发射天线
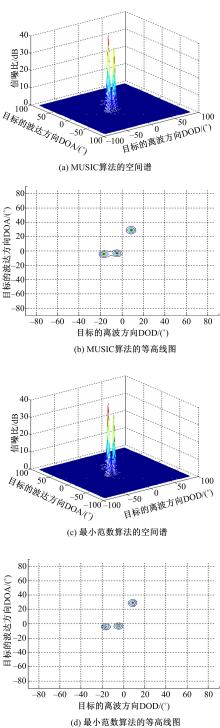
假设目标数
从图2(a)(c)可见,在信噪比为-5 dB的条件下,MUSIC算法和最小范数算法均能估计出对应目标的频谱,从图2(b)(d)可以看出,最小范数可以将目标1和目标2很好地分辨出来,而MUSIC算法就没有最小范数的分辨力强。
快拍数变化时,分析最小范数算法在DOA和DOD上的估计性能,并与MUSIC算法比较。
定义
同理,定义:
式中:
假定有4个目标,即
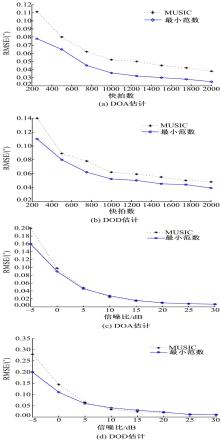
图3(a)(b)为MUSIC算法和最小范数算法对DOA和DOD的角度估计随快拍数变化的均方根误差。由该误差曲线可以看出,MUSIC算法和最小范数算法都随着快拍数的增加而获得较高的估计精度,但最小范数估计精度相对较高。
图3(c)(d)为随信噪比变化时,MUSIC算法和最小范数算法对DOA和DOD的均方根误差。由图可知,在低信噪比时,最小范数算法对DOA与DOD的估计性能优于利用MUSIC算法的估计性能;但是最小范数算法随着信噪比的增大,其估计性能会下降,达到某值以后,与MUSIC算法估计性能基本相同。
讨论了双基MIMO雷达波达方向估计问题,提出了最小范数算法,实现了双基MIMO雷达DOA和DOD的联合估计。最小范数算法利用双基MIMO雷达的联合导向矢量矩阵与噪声子空间正交,用噪声子空间的全部噪声奇异矢量构成最小范数矢量,这样就避免了MUSIC算法中由于谱峰搜索带来的计算量大的问题,而且还减少了噪声奇异矢量本身的误差,使谱峰更陡峭,提高了对参数估计的精度。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|