作者简介:燕学智(1972-),男,副教授.研究方向:信号参量估计.E-mail:yanxz@jlu.edu.cn
提出一种基于对称均匀线阵与二阶循环统计量相结合的远近场混合源定位新方法。该方法首先将均匀线阵划分为两个对称子阵,获得仅包含方位角信息的旋转矩阵,以此为基础,构造谱峰搜索函数,实现远场源和近场源角度的同时估计,将获得的方位角信息代入二维MUSIC谱函数,实现近场源距离估计。所提算法计算复杂度低,估计精度较高,且无需参数配对及二维搜索。均方根误差的仿真结果验证了该算法的有效性。
Based on the symmetric Uniform Linear Array (ULA) and the second-order cyclic statistic, an efficient algorithm is proposed to deal with the localization of the mixed far-field and near-field cyclostationary sources. First, by exploiting the symmetric property of the divided subarrays, a rotational matrix is constructed, in which only the Direction-of-Arrival (DOA) information is contained. Then, the DOA estimations for both far-field and near-field sources are performed from a spectral search procedure. Finally, by substituting the obtained azimuth back into the two-dimensional MUSIC spectral function, the range estimations for the near-field sources is performed. Compared with previous works, the proposed algorithm saves computation cost, provides high estimation accuracy, and requires neither two-dimensional search nor parameter-pairing procedure. Computer simulations confirm the feasibility of the proposed algorithm.
依据观测目标与接收阵列之间的距离远近,信源定位主要分为远场源定位[ 1](主要是波达方向估计)和近场源定位[ 2]两种。当信源与传感器阵列之间的距离
本文考虑观测目标为循环平稳信号的情况,提出一种可有效解决远近场混合循环平稳信源定位问题的新方法。该算法将均匀线阵划分成两个对称子阵,利用两对称子阵间的旋转矩阵仅与角度有关的特性,构造一个与信号子空间相关的旋转矩阵,通过重构谱峰搜索函数同时求解远场源和近场源的角度参数,在此基础上,将获得的方位角信息代入二维MUSIC谱函数,无需参数配对及二维搜索就可实现近场源距离估计。与文献[10]相比,本文算法可有效提高参量估计精度,降低计算复杂度且能抑制循环平稳干扰和平稳噪声。与文献[11]相比,本文算法可明显提高参量估计精度。
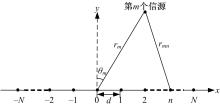
如图1所示,考虑
式中:
式中:
若第
由于远场源时距离相对很大(
将式(1)表示为矩阵形式:
式中:
假设有
为保证算法的可行性,作如下假设:①信源信号为相互独立的窄带循环平稳随机过程。②加性背景噪声为平稳过程,且与信号独立。③阵元间距
本文将均匀线阵分成两个对称子阵,选取前
子阵2观测数据矩阵为:
式中:
根据前面假设及二阶循环相关函数定义[ 12],接收数据二阶循环相关矩阵
它的第
式中:
对循环相关矩阵
式中:
由式(4)易知,存在一个
式中:
根据广义ESPRIT算法[ 13]构造旋转矩阵:
当
式中:
只需通过一维搜索就能实现远场源和近场源角度的同时估计,并且充分利用循环相关矩阵的全部信息,就提高了算法的估计性能。
前面的估计角度
理论上谱峰搜索时近场源角度
(1)计算复杂度
本文算法相对文献[10]具有更低的计算复杂度,而相比文献[11]本文计算复杂度略高,为了说明这一问题,考虑二阶统计量矩阵构建、特征值或奇异值分解以及谱峰搜索涉及的主要乘法次数。文献[10]需构造一个
文献[11]需构造两个
本文算法只需构造一个
式中:
(2)参数估计精度
文献[10]在估计近场角度时,仅利用观测数据协方差矩阵的交叉对角线元素,并将其划分为
(3)抑制平稳噪声及循环平稳干扰
文献[10]利用协方差矩阵的交叉对角线元素构造一维谱峰搜索函数,实现信源参量估计,适用于高斯白噪声,对平稳噪声及循环平稳干扰比较敏感。文献[11]利用三阶循环相关矩阵特性,根据信源的循环平稳特性,设定循环频率,能滤除平稳噪声及循环平稳干扰。本文算法充分利用二阶循环相关矩阵的全部信息,同样能有效滤除平稳噪声及循环频率不同的循环平稳干扰。
仿真实验中,信源数
本文所有仿真信噪比(SNR)与均方根误差(Root mean square error,RMSE)定义分别为:
式中:
实验一 验证本文算法在指数分布噪声通过参数为(-1.8,0.9)的二阶AR模型产生的非高斯色噪声下的参量估计性能。两个信源的方位角与距离参数为
 | 图2 非高斯色噪声下参数均方根误差随信噪比的变化曲线Fig.2 RMSE of estimated parameters versus SNR under the color non-Gaussian noise |
 | 图3 非高斯色噪声下参数均方根误差随快拍数的变化曲线Fig.3 RMSE of estimated parameters versus snapshots number under the color non-Gaussian noise |
实验二 验证本文算法在循环平稳干扰下的参量估计性能。两个信源的方位角与距离参数为
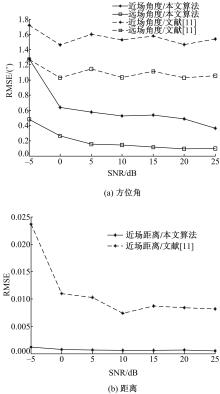 | 图4 循环平稳干扰下参数均方根误差随信噪比的变化曲线Fig.4 RMSE of estimated parameters versus SNR under the cyclostationarity interference |
 | 图5 循环平稳干扰下参数均方根误差随快拍数的变化曲线Fig.5 RMSE of estimated parameters versus snapshots number under the cyclostationarity interference |
仿真及分析结果表明:
(1)由图2和图3可知,在非高斯色噪声条件下,本文算法对角度和距离均具有良好的性能且明显优于文献[10]和文献[11]。在快拍数一定的条件下,随着信噪比的提高,混合源角度和距离的均方根误差明显减小。在信噪比一定的条件下,混合源角度和距离的均方根误差同样随快拍数增加而减小。可见本文算法有效抑制了加性平稳噪声,提高了估计精度。
(2)由图4和图5可知,相比文献[11],本文算法对循环平稳干扰具有更好的抑制能力。快拍数一定时,混合循环平稳信源参量的均方根误差随信噪比的提高而减小。当SNR达到0 dB时,远近场角度的RMSE分别低于0.578°和0.637°,近场距离的RMSE低于0.0007
(3)从两个实验的角度和距离均方根误差变化曲线可以看出,所提算法在低信噪比及较少快拍数下仍具有较高的参数估计精度。与文献[10]和文献[11]相比,本文算法随SNR和快拍数变化的曲线更加平滑,波动更小,稳定性更强。验证了本文混合循环平稳信源定位参量估计算法的有效性与估计性能的可靠性。
提出了一种远近场混合循环平稳信源定位参量估计方法。该方法将均匀线阵划分为两个对称子阵,获得仅包含方位角信息的旋转矩阵,以此为基础构造谱峰搜索函数,实现远场源和近场源角度的同时估计,将获得的方位角信息代入二维MUSIC谱函数,实现近场源距离估计。该算法基于二阶循环统计量,无需参数配对及二维搜索,有效降低了计算复杂度,并且充分利用循环相关矩阵的全部信息,提高了算法的估计性能。仿真实验结果表明,本文算法在低信噪比及较少快拍数下仍具有较高的参数估计精度。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|