基于DF中继的认知OFDM协作系统的资源分配算法

引用本文

赵晓晖, 沙京祺. 基于DF中继的认知OFDM协作系统的资源分配算法. 吉林大学学报:工学版, 2014, 44(5): 1481-1487[ZHAO Xiao-hui, SHA Jing-qi. Resource allocation algorithm in DF relay assisted OFDM cognitive radio systems. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1481-1487] 复制到剪切板

Permissions

基于DF中继的认知OFDM协作系统的资源分配算法

赵晓晖, 沙京祺

吉林大学通信工程学院信息科学实验室, 长春 130012

作者简介:赵晓晖(1957-),男,教授,博士生导师.研究方向:信号处理理论在通信中的应用. E-mail:xhzhao@jlu.edu.cn

基金:国家自然科学基金项目(61171079)

摘要

针对多中继认知OFDM协作系统的中继和功率分配采用的拉格朗日对偶分解法虽然具有较好的性能,但计算复杂度较高这一问题,提出了一种低复杂度的资源分配算法。该算法放宽了中继选择因子的整数约束条件,综合考虑认知用户各子载波的信道条件和对主用户的干扰进行中继选择。根据系统总功率和干扰约束的特点,提出一种次优功率分配算法对功率进行分步求解,在保证系统容量有所增加的基础上降低了算法的计算复杂度。仿真结果表明:本文提出的算法不仅保证了认知用户对主用户产生的干扰在临界值以内,而且使认知用户的系统容量得到了较大的提升,具有一定的可行性。

关键词: 通信技术; 多中继OFDM系统; 认知无线电; 中继选择; 功率分配

中图分类号:TN929 文献标志码:A 文章编号:1671-5497(2014)05-1481-07

Resource allocation algorithm in DF relay assisted OFDM cognitive radio systems

ZHAO Xiao-hui, SHA Jing-qi

Laboratory of Information Science, College of Communication Engineering, Jilin University, Changchun 130012, China

Abstract

For resource allocation in multi-relay assisted OFDM radio systems, most current relay and power allocation algorithms use Lagrangian dual decomposition technique to find the optimal solutions. This approach has good performance but the computational complexity is higher. To solve this problem, a resource allocation algorithm with low computational complexity is proposed. The proposed algorithm relaxes the integrality constraint on the relay selection factor. It takes both subcarriers channel conditions and the interference to the primary users introduced by the secondary users into account in the relay selection. A sub-optimal power allocation scheme is given on the basis of the properties of the total system power and interference constraints, in which the power allocation is conducted step by step. The system capacity is guaranteed with lower computational complexity. Simulation results show that the proposed algorithm can ensure that the interference introduced to the primary users is within the threshold, and can also improve the system capacity of the secondary users at the same time. Thus, the feasibility of the proposed algorithm is verified.

Keyword: communication technology; multi-relay-assisted OFDM systems; cognitive radio; relay selection; power allocation

Show Figures

0 引言

随着无线通信业务需求的持续增长,各种新型无线接入方式不断出现,使得无线频谱资源变得越来越稀缺。作为一种新的无线通信设计理念,认知无线电具有较高的灵活性和智能性,它能通过感知无线通信环境来发现空闲频谱资源,并实时自适应地改变系统工作参数,为实现频谱的动态共享和提高频谱利用率开辟了新的研究方向^{[ 1]}。

在带宽受限的无线信道中,多输入多输出(MIMO)通信技术^{[ 2]}通过空间分集使系统容量和传输质量有了大幅提高。然而受到节点尺寸以及发射功率的限制,使MIMO通信技术的实现变得复杂和困难,严重阻碍了多天线技术在移动通信领域中的应用和发展。而协作通信^{[ 3]}通过多用户之间共享天线和其他网络资源构造了一个虚拟多天线系统,再经分布式处理获得一定的空间分集增益,有效地解决了上述问题。因此,协作通信作为一种新型的通信模式受到人们越来越多的关注。

在协作通信系统中,中继节点的选取以及功率分配一直是人们研究的热点^{[ 4, 5, 6]}。目前对于认知OFDM协作系统^{[ 7]}的资源分配问题已经有了一些研究成果,文献[8]提出一种子载波和功率分配联合优化的资源分配算法,但其只适用于单中继认知OFDM协作系统。文献[9]采用拉格朗日对偶理论对多中继认知OFDM协作系统的中继选择及功率分配进行了研究,这种算法取得了很好的性能,但是计算复杂度很大,系统实现比较困难。文献[10]提出一种启发式的中继选择算法,这种算法放宽了中继选择因子的整数约束条件,根据不同准则定义中继选择因子,降低了计算复杂度。

本文在文献[10]的基础上,综合考虑认知用户的信道条件和对主用户的干扰进行中继选择。为了进一步降低复杂度,本文提出一种次优的分步功率分配算法。仿真结果表明,本文提出的优化算法在保证主用户服务质量不受影响的同时,使认知用户的系统容量得到了较大提升。

1 系统模型

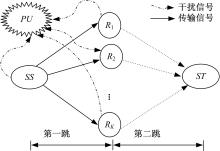
图1为一个两跳多中继认知OFDM协作系统。此系统含有一个认知用户网络和一个主用户网络,两个网络之间使用相互独立的频段进行数据传输。认知用户网络中含有一个源节点 $\begin{matrix} SS, \end{matrix}$ 一个目的节点 $\begin{matrix} ST \end{matrix}$ 和 $\begin{matrix} K \end{matrix}$ 个中继节点 $\begin{matrix} {R_{1}, R_{2}, \dots, R_{K}} 。 \end{matrix}$ 主用户网络中含有1个主用户节点 $\begin{matrix} PU 。 \end{matrix}$ 当认知用户网络中的源节点 $\begin{matrix} SS \end{matrix}$ 及各中继节点向目的节点发送数据信息时,将会对主用户网络的数据传输造成干扰,反之,主用户也会对认知用户产生干扰。本文的目标是在确保主用户服务质量的前提下,最大限度满足认知用户的发送请求。

	Figure Option View Download New Window
	图1 系统模型Fig.1 System model

假设信道衰落系数在每个传输时隙是不变的,考虑到无线信道的路径损耗特性,假定第 $\begin{matrix} l \end{matrix}$ 径衰落信道的信道衰落系数 $\begin{matrix} h_{l} \end{matrix}$ 服从复高斯分布:

$\begin{matrix} h_{l} ∶ CN (0, \frac{1}{L {(1 + d_{mn})}^{α}}) \forall l \in [1 ∶ L] (1) \end{matrix}$

式中: $\begin{matrix} d_{mn} \end{matrix}$ 为节点 $\begin{matrix} m \end{matrix}$ 到节点 $\begin{matrix} n \end{matrix}$ 的距离; $\begin{matrix} L \end{matrix}$ 为信道抽头系数; $\begin{matrix} α \end{matrix}$ 为路径损耗因子。

对式(1)进行 $\begin{matrix} N \end{matrix}$ 点FFT变换,即可得到信道增益的频域响应。

假设主用户的信道带宽为 $\begin{matrix} B, \end{matrix}$ 认知用户的信道被分成 $\begin{matrix} N \end{matrix}$ 个正交的子信道,且所有子信道均服从瑞利平坦衰落,每个子载波的带宽为 $\begin{matrix} Δf 。 \end{matrix}$ 中继节点采用半双工方式,中继方式为译码转发(DF),即将一帧分成两个等长的时隙,在第一个时隙,源节点通过广播方式将数据传输到各中继节点,在第二个时隙,中继节点对接收到的信号进行译码并经过重新编码后转发给目的节点。本文不考虑源节点和目的节点直接通信的情况,只研究源节点通过中继和目的节点进行通信的情况。假设整个系统模型中源节点、中继节点和目的节点三者都通过单天线通信。

在DF中继模式下,如果第 $\begin{matrix} i \end{matrix}$ 个子载波选择第 $\begin{matrix} k \end{matrix}$ 个中继进行译码转发,则该链路的速率可表示为:

$\begin{matrix} \begin{matrix} R_{k}^{i} = \\ \min [\frac{1}{2} lo g_{2} (1 + P_{s, i} γ_{sk, i}), \frac{1}{2} lo g_{2} (1 + P_{k, i} γ_{kd, i})] (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} P_{s, i} \end{matrix}$ 和 $\begin{matrix} P_{k, i} \end{matrix}$ 分别为源节点和第 $\begin{matrix} k \end{matrix}$ 个中继节点在第 $\begin{matrix} i \end{matrix}$ 个子载波上的发射功率; $\begin{matrix} γ_{sk, i} = \frac{{|G_{sk, i}|}^{2}}{σ_{k}^{2} + J_{k, i}} 、 γ_{kd, i} = \frac{{|G_{kd, i}|}^{2}}{σ_{d}^{2} + J_{d, i}} \end{matrix}$ 分别为第 $\begin{matrix} i \end{matrix}$ 个子载波在第 $\begin{matrix} k \end{matrix}$ 个中继节点和目的节点的瞬时信道噪声比, $\begin{matrix} σ_{k}^{2} \end{matrix}$ 和 $\begin{matrix} σ_{d}^{2} \end{matrix}$ 分别表示第 $\begin{matrix} k \end{matrix}$ 个中继节点和目的节点加性高斯白噪声(AWGN)的方差, $\begin{matrix} J_{k, i} \end{matrix}$ 和 $\begin{matrix} J_{d, i} \end{matrix}$ 分别为主用户网络对第 $\begin{matrix} k \end{matrix}$ 个中继节点和目的节点产生的干扰。

对于这个两跳多中继认知OFDM协作系统,第 $\begin{matrix} i \end{matrix}$ 个子载波对主用户网络产生的干扰可以表示为:

$\begin{matrix} \begin{matrix} I_{m, i} = \int_{d_{i}}^{-} {|G_{m, i}|}^{2} T_{s} P_{m, i} {(\frac{sinπf T_{s}}{πf T_{s}})}^{2} df = \\ P_{m, i} {|G_{m, i}|}^{2} Ω_{i} (3) \end{matrix} \end{matrix}$

式中: $\begin{matrix} d_{i} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 个子载波到主用户频段的频谱距离; $\begin{matrix} G_{m, i} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 个子载波在认知用户 $\begin{matrix} m (m \in {s, k}) \end{matrix}$ 和主用户之间的信道增益; $\begin{matrix} P_{m, i} \end{matrix}$ 为认知用户 $\begin{matrix} m \end{matrix}$ 在第 $\begin{matrix} i \end{matrix}$ 个子载波上的发射功率; $\begin{matrix} T_{s} \end{matrix}$ 为一个OFDM符号的持续时间;定义 $\begin{matrix} Ω_{i} = \int_{d_{i}}^{-} T_{s} {(\frac{sinπf T_{s}}{πf T_{s}})}^{2} df \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 个子载波对主用户的干扰因子。

相应地,主用户对认知用户的干扰可表示为:

$\begin{matrix} J_{m, i} = \int_{d_{i}}^{-} {|G_{m, i}|}^{2} γ (e^{jω}) dω (4) \end{matrix}$

式中: $\begin{matrix} γ (e^{jω}) \end{matrix}$ 为主用户的功率谱密度;根据大数定律,假设 $\begin{matrix} J_{m, i} \end{matrix}$ 为AWGN模型。

本文研究的内容是在主用户干扰门限和系统总功率的约束下,通过合理的资源优化分配最大化认知用户的系统容量。这类优化问题可以表示为:

$\begin{matrix} \begin{matrix} \max_{ρ_{k}^{i} P_{s, i}} \overset{K}{\sum_{k = 1}} \overset{N}{\sum_{i = 1}} ρ_{k}^{i} R_{k}^{i} \\ s . t . \{\begin{matrix} C 1 : \overset{K}{\sum_{k = 1}} \overset{N}{\sum_{i = 1}} ρ_{k}^{i} (P_{s, i} + P_{k, i}) \leq P \\ C 2 : \begin{matrix} P_{s, i} \geq 0, \begin{matrix} P_{k, i} \geq 0 & \forall k, i \end{matrix} \end{matrix} \\ C 3 : \overset{N}{\sum_{i = 1}} ρ_{k}^{i} P_{s, i} {|G_{s, i}|}^{2} Ω_{i} \leq I_{t h} \\ C 4 : \overset{K}{\sum_{k = 1}} \overset{N}{\sum_{i = 1}} ρ_{k}^{i} P_{k, i} {|G_{k, i}|}^{2} Ω_{i} \leq I_{th} \\ C 5 : \overset{K}{\sum_{k = 1}} ρ_{k}^{i} = 1 \begin{matrix} , & \forall i \end{matrix} \\ C 6 : ρ_{k}^{i} \in {0,1}, \begin{matrix} \forall k, i \end{matrix} \end{matrix} (5) \end{matrix} \end{matrix}$

式中: $\begin{matrix} ρ_{k}^{i} \end{matrix}$ 为中继选择因子; $\begin{matrix} C 1 \end{matrix}$ 和 $\begin{matrix} C 2 \end{matrix}$ 表示为源节点和中继节点的总功率约束条件; $\begin{matrix} I_{t h} \end{matrix}$ 为主用户网络所允许的平均最大干扰; $\begin{matrix} C 5 \end{matrix}$ 和 $\begin{matrix} C 6 \end{matrix}$ 表示每个子载波对只能选择一个中继节点。

假设第 $\begin{matrix} i \end{matrix}$ 个子载波选择中继 $\begin{matrix} k \end{matrix}$ 进行译码转发,由式(2)可知,当两跳链路速率相等时可以获得链路最大容量,也就是:

$\begin{matrix} P_{s, i} γ_{sk, i} = P_{k, i} γ_{kd, i}, P_{k, i} = η_{k}^{i} P_{s, i} (6) \end{matrix}$

式中: $\begin{matrix} η_{k}^{i} = \frac{γ_{sk, i}}{γ_{kd, i}} 。 \end{matrix}$

优化模型可以进一步转化为:

$\begin{matrix} \begin{matrix} \max_{ρ_{k}^{i} P_{s, i}} \overset{K}{\sum_{k = 1}} \overset{N}{\sum_{i = 1}} \frac{1}{2} ρ_{k}^{i} lo g_{2} (1 + P_{s, i} γ_{sk, i}) \\ s . t . \{\begin{matrix} C 1 : \overset{K}{\sum_{k = 1}} \overset{N}{\sum_{i = 1}} ρ_{k}^{i} P_{s, i} (1 + η_{k}^{i}) \leq P \\ C 2 : P_{s, i} \geq 0, \begin{matrix} \forall i \end{matrix} \\ C 3 : \overset{N}{\sum_{i = 1}} ρ_{k}^{i} P_{s, i} a^{i} \leq I_{t h} \\ C 4 : \overset{K}{\sum_{k = 1}} \overset{N}{\sum_{i = 1}} ρ_{k}^{i} P_{s, i} b_{_{k}}^{i} \leq I_{t h} \\ C 5 : \overset{K}{\sum_{k = 1}} ρ_{k}^{i} = 1 \begin{matrix} , & \forall i \end{matrix} \\ C 6 : ρ_{k}^{i} \in {0,1}, \begin{matrix} \forall k, i \end{matrix} \end{matrix} (7) \end{matrix} \end{matrix}$

式中: $\begin{matrix} a^{i} = {|G_{s, i}|}^{2} Ω_{i}, b_{k}^{i} = \frac{γ_{sk, i} {|G_{k, i}|}^{2} Ω_{i}}{γ_{kd, i}} 。 \end{matrix}$

2 资源分配算法

2.1 中继选择

在上述问题的模型中涉及了连续变量和二进制变量,这是一个混合整数规划问题,考虑到计算的复杂性,很难找到一个最优解。

本文采取一种低复杂度的中继选择算法,暂时放宽对中继选择因子 $\begin{matrix} ρ_{k}^{i} \end{matrix}$ 的整数限制,重新定义一个中继选择因子,根据中继选择因子进行最优中继选择。首先假设各子载波功率均等分配, $\begin{matrix} ξ_{k}^{i} = \frac{γ_{sk, i} γ_{kd, i}}{γ_{sk, i} + γ_{kd, i}} \end{matrix}$ 为子载波 $\begin{matrix} i \end{matrix}$ 选择中继 $\begin{matrix} k \end{matrix}$ 时的有效信干比, $\begin{matrix} a^{i} \end{matrix}$ 和 $\begin{matrix} b_{k}^{i} \end{matrix}$ 分别与源节点和中继节点 $\begin{matrix} k \end{matrix}$ 对主用户产生的干扰成正比。综合考虑认知用户的信道状况以及对主用户网络产生的干扰,可以把中继选择因子定义为:

$\begin{matrix} ρ_{k}^{i} = \frac{ξ_{k}^{i}}{a^{i} + b_{k}^{i}} (8) \end{matrix}$

式中: $\begin{matrix} ρ_{k}^{i} \end{matrix}$ 为子载波 $\begin{matrix} i \end{matrix}$ 选择第 $\begin{matrix} k \end{matrix}$ 个中继节点的有效信道增益与数据传输过程中认知用户对主用户产生干扰的比值。可以直观地看出, $\begin{matrix} ρ_{k}^{i} \end{matrix}$ 越大的中继,能够在对主用户网络产生较低干扰的条件下获得更高的容量。因此,第 $\begin{matrix} i \end{matrix}$ 个子载波选择具有最大 $\begin{matrix} ρ_{k}^{i} \end{matrix}$ 的中继作为最优中继,即:

$\begin{matrix} K (i) = \arg \max_{k} ρ_{k}^{i}, \forall i (9) \end{matrix}$

2.2 子载波配对

对于两跳链路的中继协作网络,信道的传输特性在第一跳和第二跳中可能会相差很大,这样就会在一定程度上限制系统容量。因此,在中继选择方案确定之后,令选择中继 $\begin{matrix} k \end{matrix}$ 的两跳子载波按信道增益的大小进行配对。通过子载波配对,可以进一步提高系统容量。

2.3 功率分配

前面中继选择方案确定后,在主用户干扰门限和系统总功率的约束下,可进一步对源节点和各中继节点进行功率分配。这时,优化模型转化为:

$\begin{matrix} \begin{matrix} \max_{P_{s, i}} \overset{N}{\sum_{i = 1}} \frac{1}{2} lo g_{2} (1 + P_{s, i} γ_{s k^{*}, i}) \\ s . t . \{\begin{matrix} C 1 : \overset{N}{\sum_{i = 1}} P_{s, i} (1 + η_{k^{*}}^{i}) \leq P \\ C 2 : P_{s, i} \geq 0, \forall i \\ C 3 : \overset{N}{\sum_{i = 1}} P_{s, i} a^{i} \leq I_{t h} \\ C 4 : \overset{N}{\sum_{i = 1}} P_{s, i} b_{_{k^{*}}}^{i} \leq I_{t h} \end{matrix} (10) \end{matrix} \end{matrix}$

这个问题的拉格朗日函数为:

$\begin{matrix} \begin{matrix} L = \overset{N}{\sum_{i = 1}} \frac{1}{2} lo g_{2} (1 + P_{s, i} γ_{s k^{*}, i}) + \\ λ [P - \overset{N}{\sum_{i = 1}} P_{s, i} (1 + η_{k^{*}}^{i})] + \\ μ (I_{t h} - \overset{N}{\sum_{i = 1}} P_{s, i} a^{i}) + δ (I_{t h} - \overset{N}{\sum_{i = 1}} P_{s, i} b_{k^{*}}^{i}) (11) \end{matrix} \end{matrix}$

式中: $\begin{matrix} λ > 0, μ > 0, δ > 0 \end{matrix}$ 分别是 $\begin{matrix} C 1 、 C 3 \end{matrix}$ 和 $\begin{matrix} C 4 \end{matrix}$ 约束条件的拉格朗日乘子。

求解上述问题需要求解多个拉格朗日乘子,此算法的时间复杂度为 $\begin{matrix} O (N^{3}), \end{matrix}$ 尤其当子载波个数较多时,计算量会急剧增加。因此,本文提出一种低复杂度的分步功率分配算法,并与等功率分配方案和最优功率分配方案^{[ 9]}进行性能比较。

2.3.1 分步功率分配算法

本文提出的分步功率分配算法,每次只考虑一个约束条件,对每个约束条件利用KKT条件进行求解,得到一个功率集合进而求得功率分配。

先忽略源节点和中继节点对主用户的干扰约束,只考虑总功率约束,那么优化问题转化为:

$\begin{matrix} \begin{matrix} \max \overset{N}{\sum_{i = 1}} \frac{1}{2} lo g_{2} (1 + P_{s, i} γ_{s k^{*}, i}) \\ s . t . \{\begin{matrix} \overset{N}{\sum_{i = 1}} P_{s, i} (1 + η_{k^{*}}^{i}) \leq P \\ P_{s, i} \geq 0, \forall i \end{matrix} (12) \end{matrix} \end{matrix}$

上述凸优化问题通过KKT条件^{[ 11]}进行求解,可以得到:

$\begin{matrix} P_{s, i} (T 1) = {[\frac{1}{2 \ln (2) ω_{1} (1 + η_{k^{*}}^{i})} - \frac{1}{γ_{s k^{*}, i}}]}^{+} (13) \end{matrix}$

式中: $\begin{matrix} ω_{1} = \frac{N}{2 \ln (2) (P + \overset{N}{\sum_{i = 1}} \frac{1 + η_{k^{*}}^{i}}{γ_{s k^{*}, i}})}; {[x]}^{+} = \max (0, x) 。 \end{matrix}$

类似地,分别只考虑源节点和中继节点对主用户的干扰约束条件,可得:

$\begin{matrix} P_{s, i} (T 2) = {[\frac{1}{2 \ln (2) ω_{2} a^{i}} - \frac{1}{γ_{s k^{*}, i}}]}^{+} (14) \end{matrix}$

式中: $\begin{matrix} ω_{2} = \frac{N}{2 \ln (2) (I_{t h} + \overset{N}{\sum_{i = 1}} \frac{a^{i}}{γ_{s k^{*}, i}})} 。 \end{matrix}$

$\begin{matrix} P_{s, i} (T 3) = {[\frac{1}{2 \ln (2) ω_{3} b_{k^{*}}^{i}} - \frac{1}{γ_{s k^{*}, i}}]}^{+} (15) \end{matrix}$

式中: $\begin{matrix} ω_{3} = \frac{N}{2 \ln (2) (I_{t h} + \overset{N}{\sum_{i = 1}} \frac{b_{k^{*}}^{i}}{γ_{s k^{*}, i}})} 。 \end{matrix}$

初步功率分配过程如下:

(1)对于源节点和中继节点的总功率约束条件,根据式(13)计算 $\begin{matrix} P_{s, i} (T 1) 。 \end{matrix}$

(2)对于主用户干扰约束条件,分别根据式(14)和式(15)计算 $\begin{matrix} P_{s, i} (T 2) \end{matrix}$ 和 $\begin{matrix} P_{s, i} (T 3) 。 \end{matrix}$

(3)寻找满足源节点和中继节点干扰约束的 $\begin{matrix} P'_{s, i} 。 \end{matrix}$ 如果 $\begin{matrix} P_{s, i} (T 2) \end{matrix}$ 满足主用户网络第二个时隙的干扰约束条件 $\begin{matrix} \overset{N}{\sum_{i = 1}} \end{matrix}$ P_s,i(T2) $\begin{matrix} b_{k^{*}}^{i} \end{matrix}$ ≤I _th,则令 $\begin{matrix} P'_{s, i} = P_{s, i} (T 2), \end{matrix}$ 否则 $\begin{matrix} P'_{s, i} = \min {P_{s, i} (T 2), P_{s, i} (T 3 \end{matrix}$ )}。

(4)为了使每个子载波满足所有约束条件,令源节点各子载波的发射功率为:

$\begin{matrix} P_{s, i} = \min \{P_{s, i} (T 1), P'_{s, i}\} (16) \end{matrix}$

至此,所有约束条件均已满足。但是根据上述的功率分配算法,各子载波的发射功率并不一定达到某一约束条件的临界值,也就是功率并未分配完全。因此各子载波的发射功率可进一步增加,进而认知用户网络的系统容量也可得到提高。

令 $\begin{matrix} ΔI (T 1) \end{matrix}$ 和 $\begin{matrix} ΔI (T 2) \end{matrix}$ 分别为源节点和中继节点相对于干扰临界值的残余干扰,即:

$\begin{matrix} \begin{matrix} ΔI (T 1) = I_{t h} - \overset{N}{\sum_{i = 1}} P_{s, i} a^{i} (17) \\ ΔI (T 2) = I_{t h} - \overset{N}{\sum_{i = 1}} P_{s, i} b_{k^{*}}^{i} (18) \end{matrix} \end{matrix}$

根据每个子载波对主用户产生干扰的比例进一步分配最小残余干扰,从而更新源节点各子载波的发射功率。令 $\begin{matrix} ΔI = \min {ΔI 1, ΔI 2\} \end{matrix}$ 为最小残余干扰,则源节点各子载波发射功率更新为:

$\begin{matrix} P_{s, i}^{update} = \{\begin{matrix} P_{s, i} + \frac{ΔI P_{s, i}}{\overset{N}{\sum_{i = 1}} P_{s, i} a^{i}}, ifΔI = ΔI (T 1) \\ P_{s, i} + \frac{ΔI P_{s, i}}{\overset{N}{\sum_{i = 1}} P_{s, i} b_{k^{*}}^{i}}, ifΔI = ΔI (T 2) \end{matrix} (19) \end{matrix}$

类似地,令 $\begin{matrix} ΔP \end{matrix}$ 为源节点和中继节点相对于总功率临界值的残余功率,即:

$\begin{matrix} ΔP = P - \overset{N}{\sum_{i = 1}} P_{s, i} (1 + η_{k^{*}}^{i}) (20) \end{matrix}$

根据每个子载波分得功率的比例进一步分配残余功率,从而更新源节点各子载波的发射功率,也就是:

$\begin{matrix} P_{s, i}^{update} = P_{s, i} + \frac{ΔP P_{s, i}}{\overset{N}{\sum_{i = 1}} P_{s, i} (1 + η_{k^{*}}^{i})} (21) \end{matrix}$

进一步的功率分配过程如下:

(1)分别计算 $\begin{matrix} ΔI (T 1) \end{matrix}$ 和 $\begin{matrix} ΔI (T 2) \end{matrix}$ ,找到最小的残余干扰,并根据式(19)更新源节点各子载波发射功率。

(2)如果上述求得的各子载波的发射功率不满足源节点和中继节点的总功率约束条件:

①计算残余功率 $\begin{matrix} ΔP \end{matrix}$ ,并根据式(21)更新源节点各子载波发射功率。

②如果上述求得的各子载波的发射功率不满足源节点和中继节点的干扰约束条件,则根据式(16)更新源节点各子载波发射功率。

至此,功率分配结束。分步功率分配方案的算法复杂度为 $\begin{matrix} O (N), \end{matrix}$ 与拉格朗日乘子法的算法复杂度为 $\begin{matrix} O (N^{3}) \end{matrix}$ 相比,本文提出的次优功率分配算法大大降低了计算量。

2 .3 .2 等功率分配方案

在等功率分配方案中,源节点各子载波分得相等的发射功率。根据源节点和中继节点对主用户网络的干扰约束条件,有 $\begin{matrix} P_{s, uni} (T 1) = I_{t h} (\overset{N}{\sum_{i = 1}} a^{i}) \end{matrix}$ 和 $\begin{matrix} P_{s, uni} (T 2) = I_{t h} (\overset{N}{\sum_{i = 1}} b_{k^{*}}^{i} 。) \end{matrix}$ 类似地,根据源节点和中继节点的总功率约束条件,有 $\begin{matrix} P_{s, uni} (T 3) = P / [N (1 + η_{k^{*}}^{i})] 。 \end{matrix}$ 令 $\begin{matrix} P_{s, uni} = \min {P_{s, uni} (T 1), P_{s, uni} (T 2), P_{s, uni} (T 3)}, \end{matrix}$ 至此,所得的功率分配满足源节点和中继节点的所有约束条件。

3 仿真实验与分析

本文的仿真结果是通过10 000次蒙特卡洛仿真实验统计得到的。无线衰落信道增益服从式(1)定义的复高斯指数分布,其中参数设定为 $\begin{matrix} α = 3, L = 4 。 \end{matrix}$ 主用户和认知用户分布如图2所示,认知中继随机分布在半径为r =100 m的圆形区域里,此圆形区域的圆心与源节点的距离为 $\begin{matrix} d_{sr}, \end{matrix}$ 而且同源节点和目的节点在一条直线上,中继个数 $\begin{matrix} K = 5 。 \end{matrix}$ 源节点与目的节点的距离为d =1000 m。 OFDM系统中子载波数为 $\begin{matrix} N = 8 。 \end{matrix}$

	Figure Option View Download New Window
	图2 主用户和认知用户分布Fig.2 PU and CR distribution

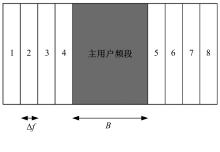
主用户和认知用户使用相邻频段,频谱分布如图3所示,带宽分别为 $\begin{matrix} B = 1 MHz, Δf = 0.3125 MHz 。 \end{matrix}$ 中继节点和目的节点的噪声方差和干扰分别为 $\begin{matrix} σ_{r}^{2} = σ_{d}^{2} = 1 \times 10^{- 14} W, J_{k, i} = J_{d, i} = 1 \times 10^{- 13} W 。 \end{matrix}$

	Figure Option View Download New Window
	图3 主用户和认知用户的频谱分布Fig.3 PU and CR distribution in frequency domain

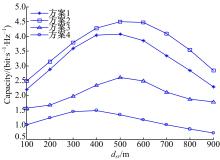
图4为系统容量在不同方案随中继位置变化的曲线。图中的方案1:采用本文的中继选择方法和次优功率分配;方案2:采用本文的中继选择方法和最优功率分配;方案3:采用随机中继选择和次优功率分配;方案4:采用本文的中继选择方法和等功率分配。仿真条件为 $\begin{matrix} P = 2 \times 10^{- 3} W, I_{t h} = 5 \times 10^{- 13} W 。 \end{matrix}$ 从图中可以看出,对于给定的主用户和认知用户分布,当中继节点分布在源节点和目的节点中点附近时,系统容量有最大值。同时方案1的系统容量远远高于方案3和方案4,说明本文提出的中继选择和功率分配方案可以获得显著的性能提升。通过方案1和方案2的比较,最优功率分配所获得的系统容量要略高于本文提出的分步功率分配所获得的系统容量,但分步功率分配算法的计算复杂度要远远小于最优功率分配。尤其当子载波个数较多时,最优功率分配的计算量会急剧增加,而本文提出的次优功率分配方案的计算量随子载波个数线性增加,与最优功率分配相比本文的次优方案更适合实际系统的实现。通过方案3和方案4的比较可知,方案3在性能上要优于方案4,可以看出在多中继协作通信系统中,在中继节点分布相对集中的情况下,相对于最优中继选择,合理的功率分配可以为系统带来更大的性能提升。

	Figure Option View Download New Window
	图4 系统容量随中继位置变化曲线Fig.4 Capacity versus relay distribution

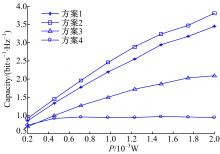
图5给出了系统容量在不同方案下随总功率约束变化的曲线。仿真条件为 $\begin{matrix} d_{sr} = 500 m, I_{t h} = 5 \times 10^{- 13} W 。 \end{matrix}$ 从图中可以看出,方案1、方案2和方案3在 $\begin{matrix} P < 1.2 \times 10^{- 3} W \end{matrix}$ 时系统容量随 $\begin{matrix} P \end{matrix}$ 的增大而线性增加,在 $\begin{matrix} P > 1.2 \times 10^{- 3} W \end{matrix}$ 时,系统容量增加相对缓慢。因为虽然系统总功率逐步增加,但此时认知用户对主用户的干扰约束条件限制了各中继节点的发射功率,从而限制了系统容量的进一步增加。同样可以看出,在方案4中 $\begin{matrix} P < 4 \times 10^{- 4} W \end{matrix}$ 时,系统容量随 $\begin{matrix} P \end{matrix}$ 的增加而线性增加;但 $\begin{matrix} P > 4 \times 10^{- 4} W \end{matrix}$ 时,系统容量基本保持不变。

	Figure Option View Download New Window
	图5 系统容量随总功率约束变化曲线Fig.5 Capacity versus power budget

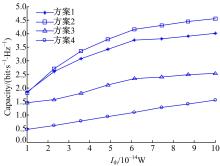
图6给出了系统容量在不同方案下随主用户干扰约束变化的曲线。仿真条件为 $\begin{matrix} d_{sr} = 500 m, P = 2 \times 10^{- 3} W 。 \end{matrix}$ 从图中可以看出:在主用户干扰约束较低时,系统容量随 $\begin{matrix} I_{t h} \end{matrix}$ 的增加线性增加;但当 $\begin{matrix} I_{t h} > 6 \times 10^{- 14} W \end{matrix}$ 时,系统容量增加缓慢。这是因为虽然逐步放宽了认知用户对主用户的干扰约束限制,但系统总功率是一定的,由于各子载波的功率之和逐步接近系统总功率,从而限制了系统容量的进一步提升。

	Figure Option View Download New Window
	图6 系统容量随干扰约束变化曲线Fig.6 Capacity versus interference threshold

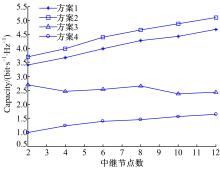
图7给出了不同方案系统容量随中继个数变化的曲线。这里取 $\begin{matrix} d_{sr} = 500 m, P = 2 \times 10^{- 3} W, I_{t h} = 5 \times 10^{- 13} W 。 \end{matrix}$ 从图中可以看出:在方案1、方案2和方案4中,系统容量随中继个数的增加而增加,这是因为系统通过增加中继节点个数获得了分集增益,使系统性能得到了一定提高。而在方案3中由于中继选择是随机的,所以中继个数的增加对系统容量并无明显影响。

	Figure Option View Download New Window
	图7 系统容量随中继个数变化曲线Fig.7 Capacity versus total numbers of relays

仿真结果表明:从各个角度考虑系统容量的增加时,本文提出的算法都具有一定的优越性,可以根据实际问题选择不同的方案来实现多中继的认知 OFDM协作系统的资源分配。

4 结束语

提出了一种低复杂度的资源分配算法。该算法放宽了中继选择因子的整数约束条件,采用认知用户各子载波的有效信道增益与对主用户网络产生干扰的比值作为中继选择的标准,并采取一种次优的功率分配算法对功率进行分步求解,从而进一步降低了计算复杂度。仿真结果表明,本文算法在保证主用户服务质量的前提下,通过中继选择和功率分配提升了认知用户的系统容量。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Mahmoud H, Yucek T, Arslan H. OFDM for cognitive radio: merits and challenges[J]. IEEE Wireless Communications, 2009, 16(2): 6-15 [本文引用:1] [JCR: 3.74]
[2]	Stuber G L, Barry J R, Mclaughlin S W, et al. Broadband MIMO-OFDM wireless communications[J]. Proceedings of the IEEE, 2004, 92(2): 271-294 [本文引用:1] [JCR: 6.911]
[3]	Rayliu K J, Sadke A, Su Wei-feng, et al. Cooperative Communications and Networking[M]. Cambridge: Cambridge University Press, 2009. [本文引用:1]
[4]	Liu Yong, Chen Wen. Limited-feedback-based adaptive power allocation and subcarrier pairing for OFDM DF relay networks with diversity[J]. IEEE Transactions on Vehicular Technology, 2012, 61(6): 2559-2571 [本文引用:1] [JCR: 2.063]
[5]	Li Yong-hui, Vucetic B, Zhou Zhen-dong, et al. Distributed adaptive power allocation for wireless relay networks[J]. IEEE Transactions on Wireless Communications, 2007, 6(3): 948-958 [本文引用:1] [JCR: 2.418]
[6]	Shaat M, Bader F. Joint subcarrier pairing and power allocation for DF-relayed OFDM cognitive systems[C]∥IEEE Global Telecommunications Conference, Houston, Texas, USA, 2011: 1-6 [本文引用:1]
[7]	Letaief K, Zhang Wei. Cooperative communications for cognitive radio networks[J]. Proceedings of the IEEE, 2009, 97(5): 878-893 [本文引用:1] [JCR: 6.911]
[8]	Sidhu G A S, Gao Feifei, Chen Wen, et al. Joint subcarrier pairing and power loading in relay aided cognitive radio networks[C]∥Wireless Communications and Networking Conference, Shanghai, 2012: 669-673 [本文引用:1] [CJCR: 0.486]
[9]	Shaat M, Bader F. Asymptotically optimal resource allocation in OFDM-based cognitive networks with multiple relays[J]. IEEE Transactions on Wireless Communications, 2012, 11(3): 892-897 [本文引用:1] [JCR: 2.418]
[10]	Bharadia D, Bansal G, Kaligineedi P, et al. Relay and power allocation schemes for OFDM-based cognitive radio systems[J]. IEEE Transactions on Wireless Communications, 2011, 10(9): 2812-2817 [本文引用:1] [JCR: 2.418]
[11]	Boyd S, Vand enberghe L. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004. [本文引用:1]

2009

3.74

0.0

... 作为一种新的无线通信设计理念,认知无线电具有较高的灵活性和智能性,它能通过感知无线通信环境来发现空闲频谱资源,并实时自适应地改变系统工作参数,为实现频谱的动态共享和提高频谱利用率开辟了新的研究方向^[1] ...

2004

6.911

0.0

... 在带宽受限的无线信道中,多输入多输出(MIMO)通信技术^[2]通过空间分集使系统容量和传输质量有了大幅提高 ...

2009

0.0

... 而协作通信^[3]通过多用户之间共享天线和其他网络资源构造了一个虚拟多天线系统,再经分布式处理获得一定的空间分集增益,有效地解决了上述问题 ...

2012

2.063

0.0

... 在协作通信系统中,中继节点的选取以及功率分配一直是人们研究的热点^[4,5,6] ...

2007

2.418

0.0

... 在协作通信系统中,中继节点的选取以及功率分配一直是人们研究的热点^[4,5,6] ...

2011

0.0

... 在协作通信系统中,中继节点的选取以及功率分配一直是人们研究的热点^[4,5,6] ...

2009

6.911

0.0

... 目前对于认知OFDM协作系统^[7]的资源分配问题已经有了一些研究成果,文献[8]提出一种子载波和功率分配联合优化的资源分配算法,但其只适用于单中继认知OFDM协作系统 ...

2012

0.0

0.486

2012

2.418

0.0

... 因此,本文提出一种低复杂度的分步功率分配算法,并与等功率分配方案和最优功率分配方案^[9]进行性能比较 ...

2011

2.418

0.0

2004

0.0

... 上述凸优化问题通过KKT条件^[11]进行求解,可以得到: ...