针对M2M业务的IEEE 802.11优化及其性能评价

引用本文

迟学芬, 马丽君, 王雅辉, 石文孝. 针对M2M业务的IEEE 802.11优化及其性能评价. 吉林大学学报:工学版, 2014, 44(5): 1488-1497[CHI Xue-fen, MA Li-jun, WANG Ya-hui, SHI Wen-xiao. IEEE 802.11 optimization and performance evaluation for M2M services. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1488-1497] 复制到剪切板

Permissions

针对M2M业务的IEEE 802.11优化及其性能评价

迟学芬, 马丽君, 王雅辉, 石文孝

吉林大学通信工程学院, 长春 130012

作者简介:迟学芬（1962-）,女,教授,博士生导师.研究方向:宽带无线IP网络的理论和技术,网络建模. E-mail:chixf@jlu.edu.cn

基金:国家自然科学基金项目(61071074); 吉林省科技发展计划项目(20130413052GH)

摘要

为降低IEEE 802.11接入过程中误码引起的竞争失败率,提出一种无退避、快速重传算法,推导了MAC层服务时间概率分布,建立了IBP/G_w/1/K离散时间排队系统,研究了非饱和负载下M2M业务在802.11非理想信道下的传输性能。为了提高海量M2M终端在802.11网络中的接入效率,提出一种动态调整窗口的算法。为模拟802.11接入和IP承载网络传输M2M业务的通信场景,基于串联排队理论,建立了多节点串联排队网络模型,并求解了M2M业务的端到端性能指标。仿真表明:两种改进算法有效提高了802.11的服务效率;异质业务接入802.11网络的场景中,突发度小的M2M业务能获得更好的QoS。

关键词: 通信技术; 服务质量; 串联排队理论; 离去过程

中图分类号:TN925 文献标志码:A 文章编号:1671-5497(2014)05-1488-10

IEEE 802.11 optimization and performance evaluation for M2M services

CHI Xue-fen, MA Li-jun, WANG Ya-hui, SHI Wen-xiao

College of Communication Engineering, Jilin University, Changchun 130012, China

Abstract

To reduce the probability of access failure caused by channel error, an algorithm featured by no backoff and fast retransmission was proposed for the access procedure of IEEE 802.11. The probability distribution of Medium Access Control (MAC) layer service was derived, and IBP/G_w/1/K discrete-time queuing model was established to analyze the QoS performance of M2M under unsaturated traffic condition and imperfect channel in the IEEE 802.11. To improve the transmission efficiency of massive M2M services, a dynamic window adjustment algorithm was put forward. Based on the tandem queuing network theory, a tandem queuing model was established to depict the real communication scenario, which was made up of wireless access network and IP core network. System end-to-end performance indicators were derived from M2M services. Simulation results indicate that the proposed algorithm can effectively improve the service efficiency of IEEE 802.11. The M2M services with low degree of burst canget better QoS when heterogeneous M2M services coexist in the network.

Keyword: communication technology; quality of service; tandem queuing theory; departure process

Show Figures

0 引言

目前,在建模和求解IEEE 802.11服务时间以及串联排队网络的研究方向上,Bianchi提出的二维马尔可夫链模型被广泛应用在有关IEEE 802.11协议DCF(Distributed coordination function)的性能分析中,但这个分析模型存在一些明显的缺陷^{[ 1]},后来很多文献改进了Bianchi的模型。Krezysztof^{[ 2]}在建模时考虑了DCF协议中信道忙时冻结退避计数器的特性;Ali^{[ 3]}提出根据前三次信道状态来改变当前竞争窗口的大小。Hung^{[ 4]}分析了隐藏终端对DCF的影响。王雅辉^{[ 5]}针对时延容忍的M2M小数据业务,提出一种大时间尺度退避的IEEE 802.11 DCF网络分析模型。高峰等^{[ 6]}针对成帧效率和DCF协议效率研究基本接入模式和请求发送/确认发送模式切换门限值。Prakash^{[ 7]}提出一种数据帧出错时不加倍窗口,只在当前退避窗口中选取退避计时器值的优化方案。为了更准确地分析网络状态,很多学者研究非理想信道下的性能^{[ 8, 9, 10, 11]}。在串联研究中,Dooyeong^{[ 12]}将IBP(Interrupted bernoulli process)模型作为串联排队网络的输入,研究了有限容量、服务时间为几何分布的排队系统的性能。Ferng^{[ 13]}用矩阵分析方法研究了有无休假的离去过程。赵莹莹建模承载M2M业务的通信网络,并求解了带有RED机制的串联排队网络模型^{[ 14]}。

M2M的业务特性与传统业务有很大的差异,给IEEE 802.11现有机制带来了挑战,为了提高802.11网络的服务性能,本文根据M2M业务特性提出两种接入改进方案:对于信道错误引起的竞争失败,采用无退避、快速重传机制来优化MAC层服务;针对M2M终端数量庞大的特性,提出根据网络负载状态动态调整退避窗口的算法。借鉴Ferng、Dooyeong等人^{[ 12, 13]}的工作,本文在异质业务背景下,建模IEEE 802.11与IP节点串联的多级网络,探索IEEE 802.11承载突发度不同的业务能力。

1 IEEE 802.11与IP承载网络

模型

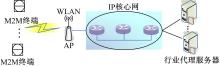M2M业务通过IEEE 802.11接入到IP承载网,网络拓扑如图1所示。本文基于串联排队理论建立M2M业务的端到端串联排队系统模型,见图2,将网络的传输过程建模成到达-排队-服务的过程。其中第一个队列代表无线网络,服务器G_w表示IEEE 802.11服务过程,后边的队列代表有线网络,服务器2到 $\begin{matrix} M \end{matrix}$ 表示IP承载网络的服务过程。

	Figure Option View Download New Window
	图1 IEEE 802.11作为接入网络时M2M业务通信场景Fig.1 M2M communication scenario when IEEE 802.11 is selected as access net

	Figure Option View Download New Window
	图2 IEEE 802.11与IP串联排队网络Fig.2 IEEE 802.11 and IP tandem que uing network

本文主要研究自动售货机、遥感监测等典型的M2M业务,这类业务具有数据量小、时延容忍、时而发包时而不发包的特性,假定每个终端的M2M小数据业务到达为IBP过程,IBP过程中,ON状态时有数据到达,OFF状态时没有任何数据到达,它适合描述M2M业务的突发性。状态转移矩阵 $\begin{matrix} R 和速率转移矩阵 Λ \end{matrix}$ 为:

$\begin{matrix} R = [\begin{matrix} p & 1 - p \\ 1 - q & q \end{matrix}], Λ = [\begin{matrix} α & 0 \\ 0 & 0 \end{matrix}] (1) \end{matrix}$

在IEEE 802.11接入部分,本文优化了媒体访问控制(Media access control,MAC)层接入算法,并推导出优化后IEEE 802.11服务时间的概率分布。有线部分应用串联排队理论,将每一个节点建模成离散时间IBP/Geom/1/K模型。图2中服务器2到 $\begin{matrix} M 服从均值为 σ \end{matrix}$ 的几何分布( $\begin{matrix} σ \end{matrix}$ 表示服务不成功的概率),系统采用先到先服务的FIFO方式服务。

2 无线接入网络建模

2.1 IEEE 802.11 MAC层服务模型改进

在IEEE 802.11标准接入过程中,不管发生错误还是碰撞,终端都根据二进制指数退避算法退避,即竞争窗口加倍后重新退避重传。在业务接入过程中,如果因碰撞数据帧没有成功发送,说明活跃的站点数比较多,将竞争窗口数加倍可以有效地缓解碰撞。但是,仅因数据帧出错没有传输成功,说明当前的退避窗口数已满足活跃站点间的竞争,加倍窗口并不能减少数据帧出错概率,反而使用户等待更长的退避时间。

针对上述问题,本文提出了改进算法1——无退避、快速重传算法,并完成理论推导。帧传输后,如果终端在短帧间间隔(Short interframe spacing,SIFS)内收到确认帧ACK,则此帧传输成功,若没收到确认,则数据帧出错或碰撞,本文根据文献[15]的方法区分误码与碰撞。若数据帧发生误码并且没有发生碰撞,不进行退避,直接占用信道重传;若数据帧出错后超过最大重传次数仍传输失败,或者数据帧发生碰撞,将按照二进制指数算法进行退避、重传。

将每个数据帧在IEEE 802.11中传输过程建模成二维的Markov链。 $\begin{matrix} b (t) 表示在时隙 t 当前站点退避计时器取值过程, b (t) \in (0,1, \dots, W_{i} - 1), 为了增加网络发包的随机性, 在 [0, W_{i} - 1] \end{matrix}$ 服从均匀分布,即 $\begin{matrix} p_{W_{i}, k} = 1 / W_{i}, s (t) 为在时隙 t 数据帧的退避级数, s (t) \in (0,1, \dots, α), 其中 α 为碰撞时最大退避次数, 设最大退避次数为 m 。 \end{matrix}$ 每次发送数据帧时,在竞争窗口中按均匀分布随机选择一个退避值,在下个时隙,当监听到信道中有数据帧传输但没有发生碰撞,计数器冻结 T_s时间;若监听到信道中发生碰撞,计数器冻结 T_c时间;若信道空闲,则退避窗口减1,直至减到0时开始发包。

$\begin{matrix} \begin{matrix} P \{i_{1}, k_{1} | i_{0}, k_{0}\} = \\ P_{r} \{s (t + 1) = i_{1}, b (t + 1) = k_{1} | s (t) = i_{0}, \\ b (t) = k_{0}\} \end{matrix} \end{matrix}$

一步转移概率可以表示为:

$\begin{matrix} \{\begin{matrix} P \{i, k | i, k + 1\} = 1 \\ k \in [0, W_{i} - 2], i \in [0, α] \\ P \{0, k | i, 0\} = (1 - p) / W_{0} \\ k \in [0, W_{0} - 1], i \in [0, α - 1] \\ P \{i, k | i - 1,0\} = p / W_{i} \\ k \in [0, W_{i} - 1], i \in [1, α] \\ P \{0, k | α, 0\} = 1 / W_{0} \\ k \in [0, W_{0} - 1] \end{matrix} (2) \end{matrix}$

式中: $\begin{matrix} p \end{matrix}$ 为每次准备传输数据帧但失败的概率。

假定 $\begin{matrix} p \end{matrix}$ 值始终恒定; p_c为任意时隙发生碰撞的概率; p_e为数据差错概率,则有:

$\begin{matrix} \begin{matrix} p = p_{c} + p_{e}^{m + 1} (1 - p_{c}) (3) \\ p_{c} = 1 - {[1 - (1 - p_{0}) τ]}^{n - 1} (4) \\ p_{e} = 1 - \overset{N_{\max}}{\sum_{n = N_{\min}}} f (n) {(1 - ε)}^{8 n} (5) \end{matrix} \end{matrix}$

式中: $\begin{matrix} p_{0} \end{matrix}$ 为没有包要发送的概率; $\begin{matrix} ε \end{matrix}$ 为比特差错率; $\begin{matrix} f (i) \end{matrix}$ 为帧长度的概率分布函数,单位均为Byte。

当退避计数器为0,开始发包,数据帧出错重传 $\begin{matrix} i 次成功传输的概率为 p_{i}, 其中最大重传次数为 m, 则有 : p_{i} = (1 - p_{c}) p_{e}^{i} (1 - p_{e}), i \in (0, \dots, m), 达到最大重传次数仍传输失败的概率 p_{m 1}, 则 p_{m 1} = (1 - p_{c}) p_{e}^{m + 1} 。 \end{matrix}$

通过对二维马尔可夫链的求解(详见文献[16]),可以得到发包概率 $\begin{matrix} τ : \end{matrix}$

$\begin{matrix} \begin{matrix} τ = \\ \{\begin{matrix} [2 (1 - 2 p) (1 - p^{α + 1})] / \\ [W (1 - {(2 p)}^{α + 1}) (1 - p) + \\ (1 - 2 p) (1 - p^{α + 1})], \\ α \leq m \\ [2 (1 - 2 p) (1 - p^{α + 1})] / \\ [W (1 - {(2 p)}^{m + 1}) (1 - p) + \\ (1 - 2 p) (1 - p^{α + 1}) + \\ 2^{m} W p^{m + 1} (1 - 2 p) (1 - p^{α - m})], \\ α > m \end{matrix} (6) \end{matrix} \end{matrix}$

2.2 MAC层服务时间

将IEEE 802.11网络的传输过程看成一个时延传输系统,数据帧从离开队列时刻到数据帧发送成功或失败的过程就是网络的服务时间。本文先分别求出发送过程、退避计数器递减过程所需时间,然后根据网络传输过程的时延框图求解数据帧在MAC层的服务时间。

由于M2M数据量小,本文采用基本方式传输M2M业务,在基本传输机制中成功传输一个数据帧的时间 T_s为:

$\begin{matrix} \begin{matrix} T_{s} = DIFS + (i + 1) (DAT A_{s} + ACK + SIFS) \\ i \in (1, \dots, m) (7) \end{matrix} \end{matrix}$

式中: DATA_s为成功传输数据帧所需时间; DIFS(DCF interFrame spacing)为分布式协调帧间间隔。

数据帧出错时,改进主要体现在数据帧传输时间、 SIFS、等待确认时间增加 $\begin{matrix} i \end{matrix}$ 倍。数据帧冲突的持续时间 T_c为:

$\begin{matrix} T_{c} = SIFS + DIFS + DAT A_{c} + ACK (8) \end{matrix}$

式中: DATA_c为发生碰撞数据帧的传输时间。

设 σ_min、 σ_max分别为最大数据帧和最小数据帧的长度。则改进后 T_s的概率生成函数包括两种情况,一部分是数据帧成功传输 $\begin{matrix} S_{0} (z) : \end{matrix}$

$\begin{matrix} \begin{matrix} S_{0} (z) = \\ \overset{m}{\sum_{i = 0}} \frac{p_{i}}{1 - p_{c}} [\overset{σ_{\max}}{\sum_{j = σ_{\min}}} f (j) z^{(i + 1) (j + ACK + SIFS) + DIFS}] \\ (9) \end{matrix} \end{matrix}$

另一部分是出错达到最大重传次数后,仍接入失败 $\begin{matrix} S_{1} (z) : \end{matrix}$

$\begin{matrix} S_{1} (z) = \frac{p_{m 1}}{1 - p_{c}} \overset{σ_{\max}}{\sum_{j = σ_{\min}}} f (j) z^{(i + 1) (j + ACK + SIFS) + DIFS} (10) \end{matrix}$

T_c由最长的碰撞帧决定,假定3个或更多帧同时碰撞的概率可以忽略,则有:

$\begin{matrix} C (z) = z^{SIFS + DIFS + ACK} \overset{σ_{\max}}{\sum_{i = σ_{\min}}} (2 f (i) F_{Y} (i) - f {(i)}^{2}) z^{i} (11) \end{matrix}$

式中: $\begin{matrix} f (i) 为数据帧长度的概率密度函数; F_{Y} (i) 为 f (i) \end{matrix}$ 的概率累积分布函数。

将数据帧在MAC层的传输过程看成 $\begin{matrix} z \end{matrix}$ 域时延系统^{[ 16]},则改进算法后IEEE 802.11 MAC层服务时间的概率生成函数为:

$\begin{matrix} \begin{matrix} G (z) = (1 - p) S_{0} (z) \cdot \\ \overset{α}{\sum_{i = 0}} \{{[p_{c} C (z) + (p - p_{c}) S_{1} (z)]}^{i} \overset{i}{\prod_{j = 0}} H_{j} (z)\} + \\ {[p_{c} C (z) + (p - p_{c}) S_{1} (z)]}^{α + 1} \overset{α}{\prod_{j = 0}} H_{j} (z) (12) \end{matrix} \end{matrix}$

令 $\begin{matrix} μ^{- 1} \end{matrix}$ 为MAC层的平均服务时间,由概率生成函数的性质,有 $\begin{matrix} μ^{- 1} = E [G_{w}] = \frac{dG (z)}{dz} |_{z = 1} 。 \end{matrix}$

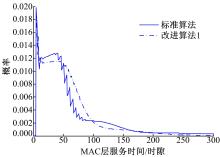
图3是站点数 n=5时MAC层服务时间的概率分布对比图,其中标准算法平均服务时间的均值为86.8586个时隙,改进算法1平均服务时间均值为62.7611个时隙。改进算法的平均服务时间小于标准算法的平均服务时间,使数据获得更快的服务速率。这是因为标准算法中数据帧发生误码或碰撞,竞争窗口都加倍,导致服务时间变化间隔比较大,因此服务时间出现剧烈抖动,而改进算法在数据帧出错时采用无退避、快速重传,避免了不必要的退避时延,服务时间的PDF变化曲线比标准算法平缓。

	Figure Option View Download New Window
	图3 MAC层服务时间的PDFFig.3 Probability distribution of MAC layer service time

2.3 动态调整退避窗口

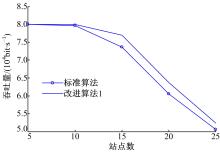
M2M终端数量巨大,本文仿真了当竞争站点数变化时标准算法和改进算法1吞吐量的变化规律。

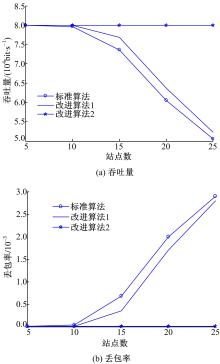
从图4中可以看出,改进算法1网络的吞吐量大于标准算法的吞吐量,提高了网络的传输性能。但是,当竞争站点数不断增加时,两种算法的吞吐量都迅速下降,这是由于当竞争站点数增加时,网络的碰撞概率变大,业务由于碰撞而传输失败。M2M终端数量巨大,当海量终端的M2M业务接入到网络时,网络的吞吐量会迅速恶化,不适合用于传输M2M业务。针对业务特点选择接入网络,是无线资源分配的重要问题,为了保证当海量终端的M2M业务接入网络后,网络仍然有很好的传输性能,本文在改进算法1的基础上提出了改进算法2——动态调整退避窗口算法,即业务在IEEE 802.11网络中传输时区分误码和碰撞,并根据网络负载状态自适应地选择最佳的退避窗口,使网络的传输性能达到最优。

	Figure Option View Download New Window
	图4 吞吐量随站点数变化Fig.4 Throughput changes with site numbers

在IEEE 802.11 DCF协议中,所有终端共享信道,通过竞争接入的方式独占信道传输数据,即每个时隙最多只有一个终端接入成功。为保证每个终端的公平性,当网络中有 $\begin{matrix} n \end{matrix}$ 个终端同时发起竞争接入时,若保证每个终端都能以最大的概率接入到网络,则每个终端在每个时隙的接入概率为 $\begin{matrix} 1 / n 。 \end{matrix}$ 因此,当网络的发包概率为 $\begin{matrix} 1 / n \end{matrix}$ 时,既能保证每个用户公平地接入到信道,而且又能使每个用户在每个时隙的发包概率最大。

当 $\begin{matrix} τ = 1 / n \end{matrix}$ 时,根据式(4)可得碰撞概率 p_c为:

$\begin{matrix} p_{c} = 1 - {[1 - \frac{1 - p_{0}}{n}]}^{n - 1} (13) \end{matrix}$

根据式(6)可以推出退避窗口 $\begin{matrix} W : \end{matrix}$

$\begin{matrix} W = \{\begin{matrix} [\frac{2}{τ} (1 - 2 p) (1 - p^{α + 1}) - \\ (1 - 2 p) (1 - p^{α + 1})] / \\ [(1 - {(2 p)}^{α + 1}) (1 - p)], \\ α \leq m \\ [\frac{2}{τ} (1 - 2 p) (1 - p^{α + 1}) - \\ (1 - 2 p) (1 - p^{α + 1})] / \\ [(1 - {(2 p)}^{m + 1}) (1 - p) + \\ 2^{m} p^{m + 1} (1 - 2 p) (1 - p^{α - m})], \\ α \geq m \end{matrix} (14) \end{matrix}$

根据网络负载状态,为网络选择最佳的退避窗口数 $\begin{matrix} W, \end{matrix}$ 使终端以更快的速度接受服务,提高网络的传输效率。

2.4 采用IBP/ G_w/1/K建模IEEE 802.11 DCF协议

将数据帧离开排队系统的时刻(即成功传输或失败)作为Markov链的嵌入点,在离去时刻根据嵌入式Markov链的方法求解排队模型。将M2M业务在IEEE 802.11 MAC层的传输过程建模成IBP/ G_w/1/K排队系统。每个站点都是以相同参数的IBP过程到达M2M业务,其中,服务时间是根据IEEE 802.11 MAC机制求得的一般分布 $\begin{matrix} G_{w} 。令 J (t) 表示在时隙 t \end{matrix}$ 数据帧离去瞬间IBP的状态,变量 $\begin{matrix} t 的单位是时隙; A (t) 表示在 [0, t) 时间内到达的数据帧数; P_{ij} (n, t) 表示 0 到 t 时间内到达 n 个顾客, 并且相位由 i 转移到 j \end{matrix}$ 的概率,则:

$\begin{matrix} \begin{matrix} p_{ij} (n, t) = P \{A (t) = \\ n, J (t) = j | A (0) = 0, J (0) = i\} \\ i, j \in (1,2) (15) \end{matrix} \end{matrix}$

根据IBP到达,可以得到表征矩阵 $\begin{matrix} D_{0} 和 D_{1}, 分别为在一个时隙内到达 0 个顾客的概率和到达 1 个顾客的概率。通过递推的方法求出 p (n, t) \end{matrix}$ ^{[ 13]}。

$\begin{matrix} p (n, t + 1) = p (n, t) \cdot D_{0} + p (n - 1, t) \cdot D_{1} (16) \end{matrix}$

在数据帧离去时刻分析排队系统的性能,令 $\begin{matrix} X (t) 表示时隙 t 缓存队列中的数据帧数, t_{n} 表示第 n \end{matrix}$ 个数据帧离开瞬间的时刻。令 $\begin{matrix} X_{n} = X (t_{n}^{+}), J_{n} = J (t_{n}^{+}) 分别为 t_{n} 之后的缓存队列状态和业务源所处状态, 可以称 {X_{n}, J_{n}, t \geq 0} 为嵌入马尔可夫链。队列的状态空间为 {0,1, \dots, K - 1} \times {1,2}, \end{matrix}$ 则在嵌入点可得到一步转移概率矩阵^{[ 13]}:

$\begin{matrix} P = [\begin{matrix} B_{0} & B_{1} & B_{2} & \dots & B_{K - 2} & {\bar{B}}_{K - 1} \\ A_{0} & A_{1} & A_{2} & \dots & A_{K - 2} & {\bar{A}}_{K - 1} \\ 0 & A_{0} & A_{1} & \dots & A_{K - 3} & {\bar{A}}_{K - 2} \\ ⁞ & ⁞ & ⁞ & ⁞ & ⁞ \\ 0 & 0 & 0 & \dots & A_{0} & {\bar{A}}_{1} \end{matrix}] (17) \end{matrix}$

式中: A_k= $\begin{matrix} \overset{\infty}{\sum_{t = 1}} \end{matrix}$ P $\begin{matrix} (k, t) \end{matrix}$ p $\begin{matrix} (G_{w} = t) \end{matrix}$ , $\begin{matrix} {\bar{A}}_{k} \end{matrix}$ = $\begin{matrix} \overset{\infty}{\sum_{i = k}} \end{matrix}$ A_i, $\begin{matrix} {\bar{B}}_{k} \end{matrix}$ = $\begin{matrix} \overset{\infty}{\sum_{i = k}} \end{matrix}$ B_i, B_k= $\begin{matrix} (I - D_{0})^{- 1} \end{matrix}$ D₁ A_k。

令 $\begin{matrix} π_{k, j} 为 (X_{n}, J_{n}) 的极限概率, 亦即离去时刻队列长度为 k, 业务源处于相位 j 时的稳态概率。离去时刻的稳态概率矢量 π = (π_{0}, π_{1}, \dots, π_{k - 1}), π_{k} = (π_{k, 1}, π_{k, 2}), 0 \leq k \leq K - 1, 通过求解线性系统 πp = π, πe = 1, 可以得到 π, 其中 e = {(1,1, \dots, 1)}^{T} 为全 1 的列向量, 维数与 π \end{matrix}$ 相同。

根据离去时刻的稳态解与任意时刻稳态解的关系,可以得到 $\begin{matrix} {X (t), J (t)} 任意时刻的极限概率为 x_{k, j} \end{matrix}$ ^{[ 17]}。平均到达率 $\begin{matrix} λ^{*} = θRe, θ \end{matrix}$ 是业务源处于各态的稳态概率,可以得到各 QoS参量,平均队长 $\begin{matrix} Q 、阻塞率 L 、平均等待时间 W 、吞吐量 S \end{matrix}$ 分别为:

$\begin{matrix} \begin{matrix} Q = \overset{K}{\sum_{k = 0}} k x_{k} e (18) \\ L = x_{k} e (1 - \frac{1}{u}) (19) \\ W = Q / S (20) \\ S = (1 - x_{0}) / u (21) \end{matrix} \end{matrix}$

分析无线局域网IEEE 802.11的离去过程并将其拟合成IBP源作为IP核心网络的输入,需要求出IBP源的3个参量: $\begin{matrix} p, q, α 。 \end{matrix}$ 由于IEEE 802.11标准中时隙很小,通过大量仿真试验过很多种拟合方法都不能拟合IEEE 802.11的离去过程。最后发现概率转移法^{[ 12]}可以很好地拟合时隙很小的离去过程。拟合基本思想是:当前处于激活状态,下一时刻离去后队列仍处于激活状态的总概率是 $\begin{matrix} p 。 \end{matrix}$ 当前处于非激活状态,下一时刻离去后队列仍处于非激活状态的总概率是 $\begin{matrix} q 。 \end{matrix}$ 具体实现过程如下:

$\begin{matrix} \begin{matrix} p = \frac{\sum_{(k, s) \in C} π (k, s) {\sum_{(k, s) \in C} x [(k, s) \to (\bar{k}, \bar{s})]}}{\sum_{(k, s) \in C} π (k, s)} (22) \\ q = \frac{\sum_{(k, s) \in I_{1}} π (k, s) {\sum_{(k, s) \in I_{1}} x [(k, s) \to (\bar{k}, \bar{s})]}}{\sum_{(k, s) \in I_{1}} π (k, s)} (23) \end{matrix} \end{matrix}$

式中: $\begin{matrix} π (k, s) 为离去时刻队列处于状态 s 时队长为 k 的概率; x [(k, s) \to (\bar{k}, \bar{s})] \end{matrix}$ 为从状态 $\begin{matrix} (k, s) \end{matrix}$ 转移到状态 $\begin{matrix} (\bar{k}, \bar{s}) 的概率; I_{1} = {(0,0)}; C \end{matrix}$ 为当前状态可以有顾客离去(在这里称为激活态),下一次离去后仍处于这些状态的集合。

估计出 $\begin{matrix} p 和 q 后, 可以拟合下一节点的到达率为 α = h_{d} (2 - p - q) / (1 - q), 其中 h_{d} \end{matrix}$ 是根据离去过程求得的离去率。

3 有线IP网络的建模

在有线网络中,每一个队列都建模成IBP/Geom/1/K。对于离散排队系统,服务总是开始于时隙开始时刻,服务完成在时隙结束时刻之前。一个到达的顾客只有在下一个服务时隙开始时才能接受服务(即使它到达时服务器处于空闲状态)。到达与服务的时隙大小相同,到达时刻假定在服务时隙的中间位置。由于业务源是IBP,队列长度为 $\begin{matrix} K, 所以队长的变化将是一个二维离散时间的马尔可夫链模型。队列的状态为 (s, n), s 代表的是服务时隙结束时到达过程所处的状态, s = 1,2 。 n \end{matrix}$ 代表的是在服务时隙结束时系统中队列的长度。IBP的表征矩阵 $\begin{matrix} D_{0} = (I - Λ) R, D_{1} = ΛR, 一步转移概率 Z \end{matrix}$ ^{[ 13]}为:

$\begin{matrix} Z = [\begin{matrix} R^{1} & Q^{1} & 0 & 0 & 0 & \dots \\ D & R & Q & 0 & 0 & \dots \\ 0 & D & R & Q & 0 & \dots \\ ⋱ & ⋱ & ⋱ & ⋱ & ⋱ \\ \dots & 0 & 0 & D & R & Q^{*} \\ \dots & 0 & 0 & 0 & D & R^{*} \end{matrix}] (24) \end{matrix}$

式中: $\begin{matrix} R^{1} = D_{0}; Q^{1} = D_{1}; D = D_{0} (1 - σ); R = σ D_{0} + D_{1} (1 - σ); Q = D_{1} σ; Q^{*} = D_{1} σ; R^{*} = D_{0} σ + D_{1} 。 \end{matrix}$ 通过 $\begin{matrix} yZ = y, ye = 1, \end{matrix}$ 求得处于各个状态的稳态概率。通过与IEEE 802.11网络相同的方法求出每个节点的平均队长、吞吐量、平均时延和丢包率等。

有线部分服务时间抽象为几何分布,则服务时间的生成函数为 S $\begin{matrix} (z) \end{matrix}$ = $\begin{matrix} \overset{\infty}{\sum_{n = 0}} \end{matrix} \begin{matrix} (1 - σ) \end{matrix} \begin{matrix} σ^{(n - 1)} \end{matrix}$ zⁿ= $\begin{matrix} \frac{1 - σ}{1 - σz} \end{matrix}$ ,根据文献[12]中提到的方法分析有线网络的离去过程。根据离去时间间隔 $\begin{matrix} D 与服务器空闲时间间隔 I 和服务时间 S \end{matrix}$ 的关系,有:

$\begin{matrix} D = I + S (25) \end{matrix}$

根据生成函数的性质,有:

$\begin{matrix} D (z) = z^{D} = z^{I + S} = z^{I} \cdot z^{S} = I (z) \cdot S (z) (26) \end{matrix}$

式中: $\begin{matrix} I (z) \end{matrix}$ 为服务器空闲时间的生成函数。

$\begin{matrix} \begin{matrix} I (z) = 1 - P^{+} (1,0) [1 - I_{1} (z)] - \\ P^{+} (2,0) [1 - I_{2} (z)] (27) \end{matrix} \end{matrix}$

式中: $\begin{matrix} I_{1} 、 I_{2} \end{matrix}$ 分别为系统处于(1,0)、(2,0)状态时服务器处于空闲时间的生成函数; $\begin{matrix} P^{+} (s, n) 为顾客离去后系统处于状态 (s, n) \end{matrix}$ 的概率。

求出离去时间生成函数 $\begin{matrix} D (z) 及其一阶导、二阶导和三阶导 D^{(1)} 、 D^{(2)} 和 D^{(3)}, 最后推出离去后 IBP 参数 (α, p, q) 。 \end{matrix}$

串联排队网络端到端时延和端到端丢包率为:

$\begin{matrix} \begin{matrix} W_{ETE} = \overset{M}{\sum_{i = 1}} W_{i} (28) \\ D_{ETE_prob} = 1 - \overset{M}{\prod_{i = 1}} (1 - D_{prob}^{i}) (29) \end{matrix} \end{matrix}$

式中: $\begin{matrix} W_{i} \end{matrix}$ 为串联节点 $\begin{matrix} i \end{matrix}$ 的平均排队时延; $\begin{matrix} D_{prob}^{i} \end{matrix}$ 为串联节点 $\begin{matrix} i \end{matrix}$ 的丢包率。

4 实验结果分析

4.1 IEEE 802.11网络的性能分析

IEEE 802.11无线部分仿真以IEEE 802.11b FHSS 作为物理层,采用基本接入方式,站点均处于非饱和状态,信道是非理想的。业务源为IBP模型。无线信道为时变信道,本文提出的IEEE 802.11优化方法主要用于在恶劣信道条件下提高通信质量。为此,在下面的仿真实验中无线信道误码率取为4×10^-4。信道条件越差,算法的优势越明显。仿真参数设置如下:信道速率为11 Mbit/s,物理层头部传输时间为192 s,MAC层头部传输时间为224 s,数据帧传输时间为100 s,信道差错为4×10^-4,ACK传输时间为(112+192) s,SIFS为28 μs,DIFS为128 μs,时隙为50 μs,初始竞争窗口为32。

在NS-2仿真平台上搭建承载M2M业务的WLAN,分析大量M2M业务终端并发时的网络侧包到达情况(实验室并行课题),用ON/OFF源配置M2M的发包行为,设置ON状态的平均持续时间、发包速率、包大小,模拟大量M2M业务终端在IEEE 802.11网络中的发包情况,在收集数据时,配置ON状态的系统参数使M2M终端的发包总量接近WLAN的系统容量,并将此场景下收集到的数据拟合为IBP业务源参数,拟合后的参数为 $\begin{matrix} p = 0.5, q = 0.9, 每个时隙的到达率 α 从 0.1 ~ 0.16 。缓存器的容量 K \end{matrix}$ 为20(包括正在被服务的数据帧)。图5、图6是改进算法前、后IEEE 802.11的仿真结果。从图5可以看出:当站点数不断增加时,改进算法1和标准算法的吞吐量会迅速下降,丢包率不断上升,而改进算法2的吞吐量和丢包率随站点数的增加平稳变化。这是由于网络会根据负载状态自适应选择最佳的退避窗口,保证每个用户在每个时隙以最佳的概率发包,因此吞吐量始终保持在最大值附近变化,丢包率几乎为0,有效地缓解了因竞争终端数过多而导致的网络拥塞问题。站点数越大,动态调整窗口算法的优势越明显。

	Figure Option View Download New Window
	图5 吞吐量和丢包率随站点数的变化Fig.5 Throughput and packet loss rate changes with site numbers

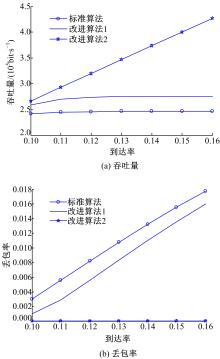
从图6可以看出:动态调整窗口算法的吞吐量会随着到达率的增加而不断增加,丢包率始终在最小值附近变化;标准算法与改进算法1的吞吐量随到达率的变化趋势平缓,但这两种算法的丢包率随到达率增加迅速增加。

	Figure Option View Download New Window
	图6 吞吐量和丢包率随到达率的变化Fig.6 Throughput and packet loss rate changes with arrival rate

4.2 串联网络的传输性能

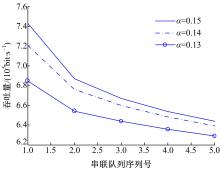
IEEE 802.11网络采用改进算法2,本节探讨802.11以及整个串联网络承载M2M业务的能力。在NS-2仿真平台上,采用与4.1节相同的方法统计M2M业务的发包情况,利用统计结果将M2M的到达拟合为IBP模型,拟合之后的参数为: $\begin{matrix} p = 0.8, q = 0.9, 到达率 α \end{matrix}$ 分别为0.15,0.14,0.13。IEEE 802.11的离去过程即为有线IP网络的第一个节点的到达过程。有线部分所有节点服务器的服务不成功的概率 $\begin{matrix} σ \end{matrix}$ 为0.985。

从图7可以看出:当到达率不变时,随着串联队列的增加,吞吐量不断下降,这是由于前边队列不断丢包(如图8所示),导致下一队列的到达率变小,因此吞吐量不断下降。在同一队列,当到达率不断增加时吞吐量也不断增加,这是由于总的到达率变大,单位时间内服务的用户数变多,因此吞吐量上升。

	Figure Option View Download New Window
	图7 吞吐量Fig.7 Throughput

	Figure Option View Download New Window
	图8 丢包率Fig.8 Packet loss rate

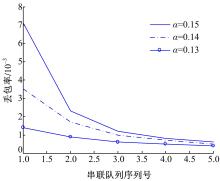
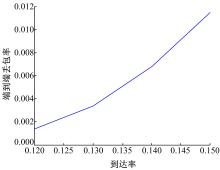
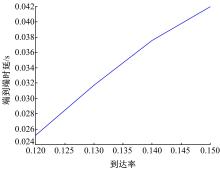
从图8可以看出:同一队列节点,随着到达率的增加,丢包率不断提高。由于有线网络所以队列的服务速率相同,随着串联节点的增加,丢包率呈下降趋势。从图9、图10可以看出:随着到达率不断增加时,端到端的丢包率和端到端的时延也不断增加。这是由于当服务速率不变时,到达率越大,缓存器溢出丢包的用户越多,用户在队列中排队等待的时间越长,这都与理论分析的结果保持一致。

	Figure Option View Download New Window
	图9 端到端的丢包率Fig.9 End-to-end packet loss rate

	Figure Option View Download New Window
	图10 端到端时延Fig.10 End-to-end delay

4.3 突发度不同的异构业务

当大量M2M业务加入到网络时,复合业务流呈现异构特性。本文针对均值相同、突发度(体现为平方变差系数SVC不同)不同时的两种业务研究其网络性能的差异。

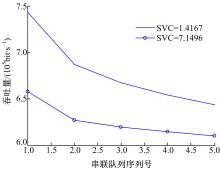
如图11所示,突发度大的业务吞吐量小于突发度小的业务的吞吐量。这是由于突发度小的业务到达比较平缓,所以丢包率也比较小,参数拟合后的到达率会比较大,所以总的吞吐量增大。

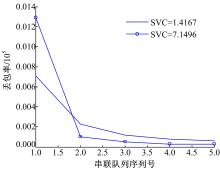
	Figure Option View Download New Window
	图11 吞吐量Fig.11 Throughput

由图12可以看出:突发度较大的业务在IEEE 802.11网络(第一个队列)丢包率比较大,因此参数拟合后的到达率变小,在有线网络服务速率不变的条件下,节点2到5的丢包率会小于突发度小的业务。这与理论分析结果保持一致。从网络吞吐量角度来看,突发度小的业务系统性能优于突发度大的业务系统性能。

	Figure Option View Download New Window
	图12 丢包率Fig.12 Packet loss rate

5 结束语

本文主要研究大量M2M业务接入IEEE 802.11网络的性能优化及评价。针对M2M小数据业务的特性,以IBP过程模拟终端M2M业务的到达分布,并提出两种IEEE 802.11改进算法。在IEEE 802.11的MAC层区分错误和碰撞丢包,数据帧出错时无退避,快速重传。数据帧碰撞时退避重传,基于二维Markov链模型研究DCF的介质访问延迟过程,推导了MAC层服务时间的概率分布,将IEEE 802.11中的M2M终端建模成一个IBP/ G_w/1/K离散时间排队系统,求解了M2M业务的排队特性。为解决海量M2M终端接入网络后吞吐量迅速恶化的问题,本文提出了动态调整窗口的算法,该算法减少了业务在IEEE 802.11中服务时间,有效地提高了网络的传输效率。另外,将承载M2M业务的通信网络建模成离散时间的串联排队网络,研究了异质业务对串联网络性能的影响。仿真结果表明:突发度小的业务在以IEEE 802.11为接入网络的串联系统中有较好的性能。在下一步的研究中,将建模LTE的服务过程,并与IEEE 802.11网络的服务性能做比较,研究异构网络准入控制的问题。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Bianchi G. Performance analysis of IEEE 802. 11 distributed coordination function[J]. IEEE Journal on Selected Areas in Communications, 2000, 18(3): 535-547. [本文引用:1] [JCR: 3.121]
[2]	Krzysztof S, Jozef L. Performance analysis of IEEE 802. 11 DCF networks[J]. Journal of Zhejiang University Science A, 2008, 9(10): 1309-1317. [本文引用:1] [JCR: 0.527] [CJCR: 0.2716]
[3]	Ali B, Ali M. The novel contention window control scheme for IEEE 802. 11 MAC protocol[C]∥The 2th International Conference on Networks Security, Wireless Communications and Trusted Computing, Wuhan, China, 2010: 134-137. [本文引用:1]
[4]	Hung F Y, Ivan M. Performance analysis of the IEEE 802. 11 DCF in the presence of the hidden stations[J]. Computer Networks, 2010, 54(15): 2674-2687. [本文引用:1] [JCR: 1.231]
[5]	王雅辉, 迟学芬. M2M小数据业务的IEEE 802. 11 WLAN分析模型[J]. 通信学报, 2011, 32(12): 122-130. Wang Ya-hui, Chi Xue-fen. IEEE 802. 11 WLAN analytical model for M2M small data service[J]. Journal on Communications, 2011, 32(12): 122-130. [本文引用:1] [CJCR: 0.595]
[6]	高峰, 高泽华, 文柳, 等. IEEE 802. 11a DCF协议吞吐量与时延性能分析[J]. 北京邮电大学学报, 2010, 33(6): 43-47. Gao Feng, Gao Ze-hua, Wen Liu, et al. Performance analysis of WLAN based on IEEE 802. 11a[J]. Journal of Beijing University of Posts and Telecommunications, 2010, 33(6): 43-47. [本文引用:1] [CJCR: 0.62]
[7]	Prakash G, Thangaraj P. Throughput analysis of IEEE 802. 11b WLAN under a non-saturated condition[C]∥International Conference and Workshop on Emerging Trends in Technology, Kochi, 2010: 298-303. [本文引用:1]
[8]	Senthilkumar D, Krishnan A. Enhancement to IEEE 802. 11 distributed coordination function to reduce packet retransmissions under imperfect channel conditions[J]. Wireless Personal Communications, 2012, 65(4) : 929-953. [本文引用:1] [JCR: 0.428]
[9]	Elena L A, Jordi C, Eduard G V. A study on the influence of transmission errors on IEEE 802. 11 IEEE 802. 11 MAC performance[J]. Wireless Communications and Mobile Computing, 2011, 11(10): 1376-1391. [本文引用:1] [JCR: 0.863]
[10]	Zhu Yi-hua, Xu Hui, Chi Kai-kai, et al. Accumulating error-free frame blocks to improve throughput for IEEE 802. 11-based WLAN[J]. Journal of Network and Computer Applications, 2012, 35(2): 743-752. [本文引用:1] [JCR: 1.467]
[11]	杨卫东, 李亚辉, 马建峰. 衰落信道中802. 11 DCF的非饱和吞吐量分析[J]. 吉林大学学报: 工学版, 2008, 38(3): 695-699. Yang Wei-dong, Li Ya-hui, Ma Jian-feng. Non-saturation throughput analysis of 802. 11 DCF in fading channel[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(3): 695-699. [本文引用:1] [CJCR: 0.701]
[12]	Dooyeong P, Harry G P. Approximate analysis of discrete-time tand em queuing networks with customer loss[C]∥In Proc IEEE GLOBE-COM'92, Orland o, Florida, 1992: 1503-1507. [本文引用:3]
[13]	Ferng Huei-Wen, Chang Jin-Fu. The departure process of discrete-time queuing systems with Markov type inputs[J]. Queuing System, 2000, 36(1-3): 201-220. [本文引用:5]
[14]	赵莹莹. 基于串联排队网理论的通信网络建模与性能分析[D]. 长春: 吉林大学通信工程学院, 2010. Zhao Ying-ying. Communication network modeling and performance analysis based on tand em queuing network theory[D]. Changchun: College of Communication Engineering, Jilin University, 2010. [本文引用:1]
[15]	Krishnan M N, Pollin S, Zakhor A. Local estimation of probabilities of direct and staggered collisions in 802. 11 WLAN[C]∥GLOBECOM-IEEE Global Telecommunications Conference, Honolulu, 2009. [本文引用:1]
[16]	王雅辉. IEEE 802. 11 IEEE 802. 11中M2M业务服务质量的研究[D]. 长春: 吉林大学通信工程学院, 2010. Wang Ya-hui. Research on quality of service of M2M in IEEE 802. 11 WLAN[D]. Changchun: College of Communication Engineering, Jilin University, 2010. [本文引用:1]
[17]	Christoph H. Complete analysis of the discrete time finite DBMAP/G/1/N queue[J]. Performance Evaluation, 2001, 43(2/3): 95-121. [本文引用:1] [JCR: 0.841]

2000

3.121

0.0

... 11协议DCF(Distributed coordination function)的性能分析中,但这个分析模型存在一些明显的缺陷^[1],后来很多文献改进了Bianchi的模型 ...

2008

0.527

0.2716

. 2008, 9(10):1309-1317 DOI:10.1631/jzus.A0720128

Performance analysis of IEEE 802.11 DCF networks

1.Warsaw University of Technology Institute of Telecommunications Nowowiejska 15/19 Warsaw 00-665 Poland

This paper presents an analytical saturation throughput model of IEEE 802.11 DCF (distributed coordination function) with basic access in ad hoc mode. The model takes into account freezing of the backoff timer when a station senses busy channel. It is shown that taking into account this feature of DCF is important in modeling saturation throughput by yielding more accurate and realistic results than models known from literature. The proposed analytical model also takes into account the effect of transmission errors. All essential features of the proposed analytical approach are illustrated with numerical results. The presentation of the model is proceeded by an overview of approaches to IEEE 802.11 network performance evaluation presented in the literature.

... Krezysztof^[2]在建模时考虑了DCF协议中信道忙时冻结退避计数器的特性 ...

2010

0.0

... Ali^[3]提出根据前三次信道状态来改变当前竞争窗口的大小 ...

2010

1.231

0.0

. 2010, 54(15):2674-2687 DOI:10.1016/j.comnet.2010.04.015

Performance analysis of the IEEE 802.11 DCF in the presence of the hidden stations

Abstract In this paper, we present an analytical model to evaluate the hidden station effect on the performance of the IEEE 802.11 Distributed Coordination Function (DCF) in both non-saturation and saturation condition. DCF is a random channel-access scheme based on Carrier Sense Multiple Access with Collision Avoidance (CSMA/CA) method and the exponential backoff procedure. DCF is widely used and can support both wireless network with an access point and ad hoc wireless network because of its random channel-access method. On the other hand, this method unavoidably suffers the hidden station effect that causes significant performance degradation. As shown in this paper, hidden stations occur frequently in real-world settings, and the performance impact on the 802.11 DCF is a significant concern, but it has not been adequately studied. We study this problem through a spatial–temporal analysis and a Markov chain model. Our model generalizes the existing work on the performance modeling of 802.11 DCF for both non-saturation and saturation conditions. The scenario of no hidden station can be considered as a special case in our model. The performance of our model is evaluated by comparison with ns-2 simulations.

... Hung^[4]分析了隐藏终端对DCF的影响 ...

2011

0.0

0.595

... 王雅辉^[5]针对时延容忍的M2M小数据业务,提出一种大时间尺度退避的IEEE 802 ...

2010

0.0

0.62

. 2010, 33(6):43-47

Performance analysis of WLAN based on IEEE 802.11a

To improve the accuracy of evaluation on IEEE 802.11a data service supporting capacity and guide network planning work, a modified twodimensional Markov chain model of the backoff window scheme is proposed. By analyzing the IEEE 802.11a wireless local area network (WLAN) system performance in the aspect of framing efficiency and distributed coordination function (DCF) efficiency, the normalized system throughput and average packet delay under the condition of saturation are found. On the basis of that, the handoff thresholds for basic access mode and request to send/clear to send (RTS/CTS) mode for diverse number of nodes are given, thus the system performance is optimized.

为了准确评估IEEE 80211a系统性能，指导同层规划工作，提出了改进二维Markov模型. 从成帧效率和分布式协调功能（DCF）协议效率2个方面对IEEE 802.11a 无线局域网（WLAN）的性能进行分析，得出饱和条件下系统归一化吞吐率和平均分组时延，并以此为基础，给出了不同节点数条件下，基本接入模式和请求发送/确认发送（RTS/CTS）模式切换门限值，使网络性能达到最优.

... 高峰等^[6]针对成帧效率和DCF协议效率研究基本接入模式和请求发送/确认发送模式切换门限值 ...

2010

0.0

... Prakash^[7]提出一种数据帧出错时不加倍窗口,只在当前退避窗口中选取退避计时器值的优化方案 ...

2012

0.428

0.0

. 2012, 65(4):929-953 DOI:10.1007/s11277-011-0320-9

Enhancement to IEEE 802.11 distributed coordination function to reduce packet retransmissions under imperfect channel conditions

1. Department of Electronics and Communication Engineering, K. S. Rangasamy College of Technology, Tiruchengode, Namakkal, TN, 637215, India

Abstract In this paper, we provide an extended model for analytical analysis of IEEE 802.11 wireless local area networks under noisy wireless channel. A reservation stage is introduced in the Markov chain model to reduce unnecessary retransmissions in the case of transmission failure due to channel error. A lot of work has been carried out to enhance the performance of 802.11 distributed coordination function in the error free channel. Throughput enhancement of 802.11 medium access control protocol under error prone channel was still missing in the available literature. Through the analysis result it is shown that the proposed method significantly improves the performance of the backoff algorithm when the reservation stage is employed in the Markov chain model. The analysis result is validated by using the network simulator tool ns-2. The proposed modifications can be employed in the Markov chain model of any backoff algorithm.

... 为了更准确地分析网络状态,很多学者研究非理想信道下的性能^[8,9,10,11] ...

2011

0.863

0.0

. 2011, 11(10):1376-1391

A study on the influence of transmission errors on WLAN IEEE 802.11 MAC performance

Elena Lopez-Aguilera * ,Jordi Casademont andEduard Garcia Villegas

Wireless Networks Group (WNG) - Telematics Department, Technical University of Catalonia (UPC), Barcelona, Spain * Wireless Networks Group (WNG) - Telematics Department, Technical University of Catalonia (UPC), Barcelona, Spain.

> Since the advent of the first IEEE 802.11 standard for WLANs, several papers have been presented that evaluate the IEEE 802.11 DCF access method. In realistic WLAN environments frame errors usually occur due to non-ideal channel conditions; in this way, papers including adverse transmission conditions in the evaluation have been published later in the literature. In this paper, we review existent analytical models that include the influence of transmission errors in IEEE 802.11 DCF performance. We modify current models and provide a more accurate analysis, thus allowing the evaluation in single rate and multi-rate scenarios with stations subject to different link error conditions. Moreover, this paper exposes the unfairness problem that arises in IEEE 802.11 DCF networks with stations subject to different transmission conditions through analytical and simulation results. Stations are not able to distinguish collisions from failed transmissions due to link errors; both result in a missing ACK and, consequently, the transmitting stations apply the exponential backoff algorithm. This fact leads to a lower performance for stations in worse transmission conditions. Copyright © 2010 John Wiley & Sons, Ltd.

... 为了更准确地分析网络状态,很多学者研究非理想信道下的性能^[8,9,10,11] ...

2012

1.467

0.0

. 2012, 35(2):null-null

Accumulating error-free frame blocks to improve throughput for IEEE 802.11-based WLAN

... 为了更准确地分析网络状态,很多学者研究非理想信道下的性能^[8,9,10,11] ...

2008

0.0

0.701

. 2008, 38(3):695-699

Non-saturation throughput analysis of 802.11 DCF in fading channel

Key Laboratory of Computer Network and Information Security，Ministry of Education, Xidian University, Xi'an 710071, China

Using a three dimensional Markov chain, a nonsaturation throughput performance model was proposed for IEEE 802.11 Distributed Coordination Function (DCF) in fading channel. The impacts of different factors, including bit error ratio, traffic loads and packet length, on the throughput of the system were analyzed using this model. Based on the model, a simple formula was derived to calculate the optimized packet length for maximizing the nonsaturation throughput. Simulation results show that this model can effectively predict the nonsaturation throughput of 802.11 DCF in fading channel, and by employing the optimum packet length the system throughput can be enhanced.

利用时间离散的三维马尔可夫链，建立了衰落信道中IEEE 802.11 DCF（分布式协调功能）在非饱和状态下的吞吐量性能模型，分析了位错误率、传输负载和分组长度对系统吞吐量的影响。基于该模型，推导了根据信道质量，计算分组长度最优值的简单公式。仿真结果表明，模型能够有效地预测802.11 DCF在衰落信道下的非饱和吞吐量，采用最优分组长度可以提高系统吞吐量。

... 为了更准确地分析网络状态,很多学者研究非理想信道下的性能^[8,9,10,11] ...

1992

0.0

... 在串联研究中,Dooyeong^[12]将IBP(Interrupted bernoulli process)模型作为串联排队网络的输入,研究了有限容量、服务时间为几何分布的排队系统的性能 ...

... 借鉴Ferng、Dooyeong等人^[12,13]的工作,本文在异质业务背景下,建模IEEE 802 ...

... 最后发现概率转移法^[12]可以很好地拟合时隙很小的离去过程 ...

2000

0.0

Queueing Systems. 2000, 36(1-3):201-220

The departure process of discrete-time queueing systems with Markovian type inputs

Huei-Wen Ferng, Jin-Fu Chang

This paper proposes a unified matrix-analytic approach to characterize the output processes of general discrete-time lossless/lossy queueing systems in which time is synchronized/slotted into fixed length intervals called slots. The arrival process can be continuous- or discrete-time Markovian processes. It can be either renewal or non-renewal. The service of a customer commences at the beginning of a slot, consumes a random number of slots, and completes at the end of a later slot. The service times are independent and follow a common and general distribution. Systems with and without server vacations are both treated in this paper. These queueing systems have potential applications in asynchronous transfer mode (ATM) networks, packet radio networks, etc. Since the output process of a node in a queueing network becomes an input process to some node at the next stage, the results of this paper can be used to facilitate end-to-end performance analysis which has attracted more and more attention in the literature.

... Ferng^[13]用矩阵分析方法研究了有无休假的离去过程 ...

... 借鉴Ferng、Dooyeong等人^[12,13]的工作,本文在异质业务背景下,建模IEEE 802 ...

... 通过递推的方法求出p(n,t)^[13] ...

... 队列的状态空间为{0,1,…,K-1}×{1,2},则在嵌入点可得到一步转移概率矩阵^[13]: ...

... IBP的表征矩阵 D0=(I-Λ)R,D1=ΛR,一步转移概率Z^[13]为: ...

2010

0.0

... 赵莹莹建模承载M2M业务的通信网络,并求解了带有RED机制的串联排队网络模型^[14] ...

2009

0.0

2010

0.0

... 将数据帧在MAC层的传输过程看成 z域时延系统^[16],则改进算法后IEEE 802 ...

2001

0.841

0.0

. 2001, 43(2/3):null-null

Complete analysis of the discrete time finite DBMAP/G/1/N queue

... 根据离去时刻的稳态解与任意时刻稳态解的关系,可以得到 {X(t),J(t)}任意时刻的极限概率为xk,j^[17] ...