认知无线电中继协助网络资源分层优化算法

引用本文

陈健, 樊光辉, 阔永红. 认知无线电中继协助网络资源分层优化算法. 吉林大学学报:工学版, 2014, 44(5): 1498-1505[CHEN Jian, FAN Guang-hui, KUO Yong-hong. Hierarchical optimization algorithm for resource allocation in relay-assisted cognitive radio network. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1498-1505] 复制到剪切板

Permissions

认知无线电中继协助网络资源分层优化算法

陈健, 樊光辉, 阔永红

西安电子科技大学通信工程学院,西安 710071

作者简介:陈健（1968-）,男,教授,博士生导师.研究方向:认知网络.E-mail:jianchen@mail.xidian.edu.cn

基金:国家自然科学基金项目(60972072,61340033); 高等学校学科创新引智计划项目（B08038）

摘要

在认知多用户中继网络系统场景下,针对时变信道完全DF中继两跳传输的差异性问题,采用纳什议价公平性准则效用函数,提出了联合用户传输模式选择、子载波配对、信道分配和功率分配的分层优化模型。利用拉格朗日对偶理论实现模型分层求解,在降低算法复杂度的同时提升了系统效用及吞吐量。仿真结果表明:相对于完全中继、直传网络和非载波配对的中继网络,所提算法在兼顾用户速率需求和公平性的同时可使系统吞吐量获得较大提高。

关键词: 通信技术; 认知无线电; 中继协助; 资源分配; 拉格朗日对偶; 分层优化

中图分类号:TN925 文献标志码:A 文章编号:1671-5497(2014)05-1498-08

Hierarchical optimization algorithm for resource allocation in relay-assisted cognitive radio network

CHEN Jian, FAN Guang-hui, KUO Yong-hong

School of Telecommunications Engineering, Xidian University, Xi'an 710071, China

Abstract

In order to diversity problem of two-hop complete Decode-and-Forward (DF) relay transmission in time-varying channels, a hierarchical optimization model is proposed. This model is based on Nash bargaining fairness criterion, and it combines transmission mode selection, subcarrier pairing, channel assignment and power allocation. Taking the advantage of Lagrange Duality, the proposed model reduces the algorithm complexity, improves the system utility and enhances the overall throughput. Simulation results show that, compared with complete relay transmission models, direct transmission models and non-carrier-pairing transmission models, the proposed algorithm achieves great improvement in system throughput and ensures the users' rate requirement and fairness at the same time.

Keyword: communication technology; cognitive radio; relay assisted; resource allocation; Lagrange dual; hierarchical optimization

Show Figures

0 引言

认知无线电是提高频谱利用率的潜在技术。认知用户通过频谱感知以机会频谱接入方式实现授权频谱的再次利用。然而频谱感知并非完美,会对主用户带来较大干扰,阻碍动态频谱接入技术的应用,引入认知中继后既可以改善链路质量,也可以降低发送功率,即降低对主用户网络的干扰,增强网络覆盖^{[ 1]},因此研究这种情况下的资源分配问题显得尤为重要。

认知中继网络资源分配场景可划分为单用户和多用户场景。针对单用户的资源分配主要是通过合理的调度机制^{[ 2]}和最优化理论^{[ 3, 4]}实现点对点系统中继选择或中继分配、载波分配和功率分配等。多用户认知中继网络资源分配在认知蜂窝网中有着重要的意义,但目前研究较少。文献[5]考虑一个中继节点只为一个用户服务的OFDMA上行链路场景下中继选择与资源分配,但未能解决中继两跳传输差异问题。文献[6]提出认知蜂窝网引入中继构成多个中继簇小区下的子载波分配和功率控制的算法,小区用户采用完全中继传输。文献[7]为兼顾用户公平性,以效用优化为目标,运用对偶理论求解完全认知DF模式下的资源分配策略,但该文献局限于所有用户都通过中继传输来提高效用容量。

上述多用户完全中继网络场景由于信道的时变特性,无法有效提高网络吞吐量。自适应选择传输模式在单用户场景^{[ 8]}得到广泛研究,但不能简单应用到多用户竞争场景,且难以确保用户的QoS及用户公平性。其次,中继两跳采用相同子载波时,存在两跳传输差异问题,通过子载波配对技术可解决该问题^{[ 9]}。基于上述分析,本文基于多个主用户共存下的认知下行OFDMA系统场景,提出自适应选择中继协助策略,为兼顾用户公平性及用户的速率需求,采用纳什议价公平性准则效用函数作为优化目标^{[ 10]},为求解该优化模型,提出分层分配框架,应用层根据当前信道状况自适应调整不同用户速率需求,物理层采用子载波对技术,自适应实现资源最佳分配。通过最优化理论分步对偶求解,有效地解决了用户传输模式选择及子载波对的资源分配问题。此外,本文提出增强型资源分配策略,有效提高了子载波的利用效率,在保证用户公平性和速率需求的同时提高了网络吞吐量。

1 系统模型

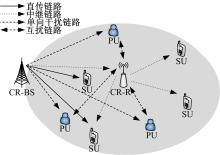
图1为认知Overlay场景下主次用户共享网络资源架构下的传输链路与干扰链路。假设中继、基站配备单天线,认知用户、认知中继节点都具有感知功能,可用频谱和信道状态信息通过认知中继向基站传递,因此在下行传输链路中,基站需根据实时信道状态为中继覆盖范围内的小区用户决策以下信息:传输模式(中继或直传)、用户载波、用户功率。认知网络采用OFDMA的TDD模式,OFDM载波间隔等分为两个时隙,认知DF中继是半双工通信。为避免干扰,在每一时隙每个子载波只能被一个认知节点使用。

	Figure Option View Download New Window
	图1 网络拓扑和信道链路Fig.1 Network topology and channel links

假设主网络用户总带宽为 $\begin{matrix} W_{T}, 有 L \end{matrix}$ 个主用户, $\begin{matrix} M \end{matrix}$ 个认知用户,1个认知中继,每一个主用户占用不同的信道带宽为 $\begin{matrix} W_{l}, l \in [1, L] 。 \end{matrix}$ 当前可用总带宽 $\begin{matrix} W \end{matrix}$ 等分为 $\begin{matrix} K \end{matrix}$ 份,每一部分的带宽为 $\begin{matrix} Δf \end{matrix}$ 。假设认知用户完美感知接入,认知用户采用OFDM调制,而主用户采用非正交调制,认知用户会对主用户带来旁瓣干扰^{[ 11]}。OFDM符号间隔为 $\begin{matrix} T_{s}, \end{matrix}$ 在子载波对 $\begin{matrix} (i, j) (i, j \in [1, K]) \end{matrix}$ 上认知基站、认知中继以单位功率发送信息时,对主用户 $\begin{matrix} l, l \in [1, L] \end{matrix}$ 的旁瓣干扰分别为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} I_{S, i}^{l} = g_{i}^{S P_{l}} T_{s} \int_{d_{i}^{l}}^{-} {(\frac{sinπf T_{s}}{πf T_{s}})}^{2} df \\ I_{R, j}^{l} = g_{j}^{R P_{l}} T_{s} \int_{d_{j}^{l}}^{-} {(\frac{sinπf T_{s}}{πf T_{s}})}^{2} df \end{matrix} \\ (1) \end{matrix} \end{matrix}$

式中: $\begin{matrix} g_{i}^{S P_{l}} 、 g_{j}^{R P_{l}} \end{matrix}$ 分别表示基站和认知中继在子载波 $\begin{matrix} (i, j) \end{matrix}$ 上对主网络用户 $\begin{matrix} l \end{matrix}$ 的干扰信道增益信息; $\begin{matrix} d_{i}^{l} \end{matrix}$ 为载波 $\begin{matrix} i \end{matrix}$ 与主用户 $\begin{matrix} l \end{matrix}$ 所占用载波的中心间距。

2 中继协助网络资源分层优化模型

在现有的基于子载波配对的认知中继资源分配策略中,由于基站分时隙实现载波占用,造成了频谱资源的浪费。与现有的载波配对策略不同,本文提出增强型的载波对分配方案,基站可在第二时隙占用认知中继尚未使用的载波直传部分额外信息,即整个直传链路和中继链路均采用子载波配对技术,从而进一步提高频谱使用效率。

子载波对用户 $\begin{matrix} (i, j, m) \end{matrix}$ 直传链路信噪比为:

$\begin{matrix} \{\begin{matrix} γ_{i, m}^{S} = h_{i}^{S D_{m}} / Γ (N_{0} Δf + \overset{L}{\sum_{l = 1}} J_{i}^{l D_{m}}) \\ γ_{j, m}^{S} = h_{j}^{S D_{m}} / Γ (N_{0} Δf + \overset{L}{\sum_{l = 1}} J_{j}^{l D_{m}}) \end{matrix} (2) \end{matrix}$

式中: $\begin{matrix} J_{i}^{lR} 、 J_{j}^{l D_{m}} \end{matrix}$ 为主用户对认知用户 $\begin{matrix} m \end{matrix}$ 在子载波对 $\begin{matrix} (i, j) \end{matrix}$ 上的单位功率干扰; $\begin{matrix} Γ \end{matrix}$ 为信噪比冗余; $\begin{matrix} N_{0} \end{matrix}$ 为加性噪声单边功率谱密度。

由式(2)可得直传链路传输速率为:

$\begin{matrix} \begin{matrix} R_{i, j, m}^{D} = \\ \frac{Δf}{2} [lo g_{2} (1 + γ_{i, m}^{S} P_{i, j, m}^{1}) + lo g_{2} (1 + γ_{j, m}^{S} P_{i, j, m}^{2})] (3) \end{matrix} \end{matrix}$

接收端根据中继链路第一时隙直传信息和第二时隙中继传输信息最大比合并,得到中继链路的速率为:

$\begin{matrix} \begin{matrix} R_{i, j, m}^{R} = \frac{Δf}{2} \min {lo g_{2} (1 + γ_{i, R}^{S} P_{i, R}^{S}), \\ lo g_{2} (1 + γ_{i, m}^{S} P_{i, R}^{S} + γ_{j, m}^{R} p_{j, m}^{R})} (4) \end{matrix} \end{matrix}$

式中: $\begin{matrix} P_{i, R}^{S} 、 P_{j, m}^{R} \end{matrix}$ 为认知基站、认知中继发送功率。

考虑发送功率总和受限,即 $\begin{matrix} P_{i, j, m}^{3} = P_{i, R}^{S} + P_{j, m}^{R}, \end{matrix}$ 当中继链路速率取最大时,必然存在下式:

$\begin{matrix} \begin{matrix} lo g_{2} (1 + γ_{i, R}^{S} P_{i, R}^{S}) = \\ lo g_{2} (1 + γ_{i, m}^{S} P_{i, R}^{S} + γ_{j, m}^{R} P_{j, m}^{R}) (5) \end{matrix} \end{matrix}$

由式(5)得到等效发送功率为:

$\begin{matrix} \{\begin{matrix} P_{i, R}^{S} = \frac{γ_{j, m}^{R}}{γ_{i, R}^{S} - γ_{i, m}^{S} + γ_{j, m}^{R}} P_{i, j, m}^{3} = γ_{i, j, m}^{S} P_{i, j, m}^{3} \\ P_{j, m}^{R} = \frac{γ_{i, R}^{S} - γ_{i, m}^{S}}{γ_{i, R}^{S} - γ_{i, m}^{S} + γ_{j, m}^{R}} P_{i, j, m}^{3} = γ_{i, j, m}^{R} P_{i, j, m}^{3} \end{matrix} (6) \end{matrix}$

在实际蜂窝网络下行通信场景中,若仅考虑系统容量最大化,基站优先将资源分配给信道质量好的用户,这种基站分配的“贪婪”特性致使系统部分用户无法满足自身传输需求。因此,本文结合用户需求及资源分配公平性,根据纳什议价原理并利用对数函数严格递增特性构建优化模型P1:

$\begin{matrix} \begin{matrix} P 1 : \max_{α, β, ρ, P, R_{\min}} \overset{M}{\sum_{m = 1}} \ln (R_{m} - R_{m, \min}) \\ s . t A 1 : R_{m} \geq R_{m, \min} m \in M \\ A 2 : \overset{M}{\sum_{m = 1}} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} (P_{i, j, m}^{1} + P_{i, j, m}^{2} + P_{i, j, m}^{3}) \leq P_{T} \\ A 3 : P_{i, j, m}^{1}, P_{i, j, m}^{2}, P_{i, j, m}^{3} \geq 0, \forall i, j, m \\ A 4 : \overset{M}{\sum_{m = 1}} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} (P_{i, j, m}^{1} + γ_{i, j, m}^{S} P_{i, j, m}^{3}) I_{S, i}^{l} \leq \\ I_{t h}^{l}, l \in [1, L] \\ A 5 : \overset{M}{\sum_{m = 1}} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} (P_{i, j, m}^{2} I_{S, j}^{l} + γ_{i, j, m}^{R} P_{i, j, m}^{3} I_{R, j}^{l}) \leq \\ I_{t h}^{l}, l \in [1, L] \\ A 6 : \overset{K}{\sum_{i = 1}} α_{i, j} = 1, \forall i \overset{K}{\sum_{j = 1}} α_{i, j} = 1, \forall j α_{i, j} \in {0,1} \\ A 7 : \overset{M}{\sum_{m = 1}} β_{i, j, m} = 1, \forall i, j, β_{i, j, m} \in {0,1} (7) \end{matrix} \end{matrix}$

式中: R_m= $\begin{matrix} \overset{K}{\sum_{i = 1}} \end{matrix} \begin{matrix} \overset{K}{\sum_{j = 1}} \end{matrix}$ α_i,jβ_i,j,m[ρ_i,j,m $\begin{matrix} R_{i, j, m}^{R} \end{matrix}$ +(1-ρ_i,j,m) $\begin{matrix} R_{i, j, m}^{D} \end{matrix}$ ];ρ_i,j,m=1,表示用户子载波对采用中继传输,反之表示直传链路传输;子载波 $\begin{matrix} (i, j) \end{matrix}$ 构成载波对时 $\begin{matrix} α_{i, j} = 1, \end{matrix}$ 否则 $\begin{matrix} α_{i, j} = 0; \end{matrix}$ 子载波对 $\begin{matrix} (i, j) \end{matrix}$ 分配给用户 $\begin{matrix} m \end{matrix}$ 时 $\begin{matrix} β_{i, j, m} = 1, \end{matrix}$ 否则 $\begin{matrix} β_{i, j, m} = 0; R_{m, \min} \end{matrix}$ 为认知用户 $\begin{matrix} m \end{matrix}$ 的速率阈值; $\begin{matrix} P_{T} \end{matrix}$ 为总功率阈值; $\begin{matrix} I_{t h}^{l} \end{matrix}$ 为主用户 $\begin{matrix} l \end{matrix}$ 可承受的干扰阈值。

3 分层优化算法描述

优化模型 P1是含有变量 $\begin{matrix} α 、 β 、 ρ 、 P 、 R_{\min} \end{matrix}$ 的混合二进制整数优化,若采用传统的耗尽搜索算法求解,当用户数和子载波数较大时,算法复杂度呈指数增长。本文基于对偶理论,采用分层对偶方案以降低模型求解复杂度。由于该优化模型非凸特性,运用对偶理论求解存在对偶间隙,但系统子载波数足够大时,通过对偶虚拟近似存在零对偶差异^{[ 12]}。

3 .1 对偶分解实现分层优化

优化模型 P1采用拉格朗日对偶求解时,直接求解具有对数特性的目标函数很困难,因此引入辅助变量 $\begin{matrix} X, X = {[X_{1}, \dots, X_{M}]}^{T}, \end{matrix}$ 则 P1等效为:

$\begin{matrix} \begin{matrix} P 2 : \max_{α, β, ρ, P, X} \overset{M}{\sum_{m = 1}} \ln (X_{m} - R_{m, \min}) \\ s . t A 2 ~ A 7, R_{m} \geq X_{m} \geq R_{m, \min} (8) \end{matrix} \end{matrix}$

显然,当 $\begin{matrix} R_{m} = X_{m} \end{matrix}$ 时, P2取到最大值,此时 P1和 P2等效。 P2中目标效用函数是每一个用户数据流可实现速率 $\begin{matrix} R_{m} \end{matrix}$ 的凹函数,因此可采用局部拉格朗日对偶求解,设 $\begin{matrix} w = [w_{1}, w_{m}, \dots, w_{M}] \end{matrix}$ 为可实现速率的拉格朗日乘子,则对偶函数 $\begin{matrix} D (w) \end{matrix}$ 可表征如下:

$\begin{matrix} \begin{matrix} \max_{α, β, ρ, P, X} L (w) = \overset{M}{\sum_{m = 1}} \ln (X_{m} - R_{m, \min}) + \\ \overset{M}{\sum_{m = 1}} w_{m} (R_{m} - X_{m}) \\ s . t . A 2 ~ A 7 (9) \end{matrix} \end{matrix}$

该优化问题可等效分解为两个子优化问题,其一为应用层的速率自适应优化问题 S1:

$\begin{matrix} \begin{matrix} S 1 : D_{appl} (w) = \\ \underset{X}{m ax} \overset{M}{\sum_{m = 1}} [\ln (X_{m} - R_{m, \min}) - w_{m} X_{m}] \\ s . t . X_{m} \geq R_{m, \min}, \forall m (10) \end{matrix} \end{matrix}$

物理层优化问题 S2涉及子载波配对、载波对分配、功率分配和传输模式选择,其表征如下:

$\begin{matrix} \begin{matrix} S 2 : D_{p h y} (w) = \max_{α, β, ρ, P} \overset{M}{\sum_{m = 1}} w_{m} R_{m} \\ s . t . A 2 ~ A 7 (11) \end{matrix} \end{matrix}$

优化问题 S1和 S2可通过对偶变量 $\begin{matrix} w \end{matrix}$ 实现速率均衡。 P2的局部对偶问题为:

$\begin{matrix} dual problem : \min D (w) s . t . w \geq 0 (12) \end{matrix}$

上述对偶问题可通过次梯度迭代更新乘子 $\begin{matrix} w \end{matrix}$ 求解^{[ 13]}。乘子 $\begin{matrix} w \end{matrix}$ 迭代更新表达式如下:

$\begin{matrix} w^{(n + 1)} = w^{(n)} - t^{T} \times (R^{*} - X^{*}) (13) \end{matrix}$

优化问题 S1中目标函数是 $\begin{matrix} X \end{matrix}$ 的严格递增函数,易求出 S1的解为 $\begin{matrix} X^{*} = \max (R_{\min}, 1 / w + R_{\min}) 。 \end{matrix}$ 下面着重分析物理层优化问题S2。

3.2 物理层优化问题求解

优化问题S2可认为是用户权重自适应变化的资源分配问题,对该问题求解先假定确知子载波匹配和子载波对分配求解功率,然后根据功率分配决策用户传输模式、载波对分配、子载波配对情况。

S2在子载波数足够大时,是一个近似存在零对偶间隙的优化问题,所以仍采用局部拉格朗日对偶分步求解,把原优化问题分解成每一个子问题,且每一个子问题都可获得近似最佳解。S2的对偶函数为:

$\begin{matrix} \begin{matrix} D (λ_{S}, μ_{1}, μ_{2}) = \max_{α, β, ρ, P} L (α, β, ρ, P_{i, j, m}^{1}, P_{i, j, m}^{2}, P_{i, j, m}^{3}) \\ s . t . A 6, A 7 (14) \end{matrix} \end{matrix}$

式中: $\begin{matrix} λ_{S} 、 μ_{1} \end{matrix}$ 和 $\begin{matrix} μ_{2} \end{matrix}$ 为拉氏乘子,分别对应约束条件A2、A4和A5。

式(14)所示的拉氏函数表征如下:

$\begin{matrix} \begin{matrix} L (α, β, ρ, P_{i, j, m}^{1}, P_{i, j, m}^{2}, P_{i, j, m}^{3}) = \\ \overset{M}{\sum_{m = 1}} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} α_{i, j} β_{i, j, m} L_{i, j, m} + λ_{S} P_{T} + \overset{L}{\sum_{l = 1}} (μ_{1}^{l} + μ_{2}^{l}) I_{t h}^{l} (15) \end{matrix} \end{matrix}$

式中: $\begin{matrix} L_{i, j, m} \end{matrix}$ 为混合链路子载波对用户 $\begin{matrix} (i, j, m) \end{matrix}$ 函数。

$\begin{matrix} \begin{matrix} L_{i, j, m} = w_{m} R_{i, j, m} - λ_{S} (P_{i, j, m}^{1} + P_{i, j, m}^{2} + P_{i, j, m}^{3}) - \\ \overset{L}{\sum_{l = 1}} μ_{1}^{l} I_{S, i}^{l} (P_{i, j, m}^{1} + γ_{i, j, m}^{S} P_{i, j, m}^{3}) - \\ \overset{L}{\sum_{l = 1}} μ_{2}^{l} (P_{i, j, m}^{2} I_{S, j}^{l} + γ_{i, j, m}^{R} P_{i, j, m}^{3} I_{R, j}^{l}) (16) \end{matrix} \end{matrix}$

式(14)的对偶函数对应的对偶问题为:

$\begin{matrix} \begin{matrix} dual problem : \min_{λ_{S} \geq 0, μ_{1}, μ_{2} \geq 0} D (λ_{S}, μ_{1}, μ_{2}) \\ s . t . A 6, A 7 (17) \end{matrix} \end{matrix}$

欲求得式(17)最佳解,需做以下分析:假定确知子载波对匹配、用户子载波对分配,式(15)可分解成 $\begin{matrix} M K^{2} \end{matrix}$ 个功率分配子问题。每一个子问题分别得到最优解即式(16)函数取到最大值时,对偶问题取得最优解。因此最佳功率分配可通过求解如下子问题得到:

$\begin{matrix} \begin{matrix} \max_{P_{i, j, m}^{1,2, 3}} L_{i, j, m} \\ s . t . P_{i, j, m}^{1}, P_{i, j, m}^{2}, P_{i, j, m}^{3} \geq 0 (18) \end{matrix} \end{matrix}$

依据式(18)并运用KKT条件可以求得优化模型(17)的功率分配如下:

$\begin{matrix} \{\begin{matrix} P_{i, j, m}^{1 *} = (1 - ρ_{i, j, m}) [w_{m} / 2 \ln 2 (λ_{S} + \\ \overset{L}{\sum_{l = 1}} μ_{1}^{l} I_{S, i}^{l}) - 1 / γ_{i, m}^{S}]^{+} \\ P_{i, j, m}^{2 *} = (1 - ρ_{i, j, m}) [w_{m} / 2 \ln 2 (λ_{S} + \\ \overset{L}{\sum_{l = 1}} μ_{2}^{l} I_{S, j}^{l}) - 1 / γ_{j, m}^{S}]^{+} \\ P_{i, j, m}^{3 *} = ρ_{i, j, m} [w_{m} / 2 \ln 2 (λ_{S} + \\ \overset{L}{\sum_{l = 1}} μ_{1}^{l} I_{S, i}^{l} γ_{i, j, m}^{S} + \overset{L}{\sum_{l = 1}} μ_{2}^{l} I_{R, j}^{l} γ_{i, j, m}^{R}) - 1 / γ_{i, j, m}] \end{matrix} (19) \end{matrix}$

式中: $\begin{matrix} {[x]}^{+} = \max (x, 0) 。 \end{matrix}$

(1)用户传输模式选择

由式(16)可分别求出子载波对用户采用直传链路传输和中继链路传输下函数值,即:

$\begin{matrix} \begin{matrix} L_{i, j, m}^{R} = \frac{1}{2} w_{m} lo g_{2} (1 + γ_{i, j, m} P_{i, j, m}^{3 *}) - \\ (λ_{S} + \overset{L}{\sum_{l = 1}} μ_{1}^{l} I_{S, i}^{l} γ_{i, j, m}^{S} + \overset{L}{\sum_{l = 1}} μ_{2}^{l} I_{R, j}^{l} γ_{i, j, m}^{R}) P_{i, j, m}^{3 *} (20) \\ L_{i, j, m}^{D} = \frac{w_{m}}{2} [lo g_{2} (1 + γ_{i, m}^{S} P_{i, j, m}^{1 *}) + \\ lo g_{2} (1 + γ_{j, m}^{S} P_{i, j, m}^{2 *})] - \\ (λ_{S} + \overset{L}{\sum_{l = 1}} μ_{1}^{l} I_{S, i}^{l}) P_{i, j, m}^{1 *} - (λ_{S} + \overset{L}{\sum_{l = 1}} μ_{2}^{l} I_{S, j}^{l}) P_{i, j, m}^{2 *} (21) \end{matrix} \end{matrix}$

若 $\begin{matrix} L_{i, j, m}^{R} \geq L_{i, j, m}^{D}, \end{matrix}$ 则 $\begin{matrix} ρ_{i, j, m}^{*} = 1, \end{matrix}$ 用户采用中继传输;反之, $\begin{matrix} ρ_{i, j, m}^{*} = 0, \end{matrix}$ 用户采用直传链路传输。故每个子载波对用户可实现的最大函数值为:

$\begin{matrix} L_{i, j, m}^{*} = ρ_{i, j, m}^{*} L_{i, j, m}^{R} + (1 - ρ_{i, j, m}^{*}) L_{i, j, m}^{D} (22) \end{matrix}$

(2)用户子载波对分配

每一个子载波对只能分给一个最佳用户,因此在得到用户传输模式的情况下选择最佳用户与子载波对匹配,使对偶函数值取到最优。把式(22)代入到对偶问题中建立下述优化问题:

$\begin{matrix} \begin{matrix} D (λ_{S}, μ_{1}, μ_{2}) = \\ \max_{α, β} \overset{M}{\sum_{m = 1}} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} α_{i, j} β_{i, j, m} L_{i, j, m}^{*} + \\ λ_{S} P_{T} + \overset{L}{\sum_{l = 1}} (μ_{1}^{l} + μ_{2}^{l}) I_{t h}^{l} \\ s . t . A 6, A 7 (23) \end{matrix} \end{matrix}$

欲使优化问题(23)取得最大值,应使函数 $\begin{matrix} L_{i, j, m}^{*} \end{matrix}$ 值最大,即把子载波对 $\begin{matrix} (i, j) \end{matrix}$ 和最佳用户 $\begin{matrix} m \end{matrix}$ 相匹配。因此可得到下述优化目标:

$\begin{matrix} \max_{α, β} L_{i, j, m}^{*} s . t . A 6, A 7 (24) \end{matrix}$

通过求解优化问题(24),可得到每一个子载波对上的最佳用户,即 $\begin{matrix} m^{*} = \underset{m \in [1, M]}{argmax} L_{i, j, m}^{*}, \end{matrix}$ 此时得到最佳子载波对分配因子 $\begin{matrix} β_{i, j, m^{*}} = 1, 反之 β_{i, j, m^{*}} = 0 。 \end{matrix}$ 每一个可行子载波对都可分配到一个最佳用户。

(3)最佳子载波对匹配

由式(24)得到每一个子载波对上的最大函数值,即 $\begin{matrix} L_{i, j} = \max_{m \in [1, M]} L_{i, j, m^{*}}^{*}, \end{matrix}$ 将其代入对偶问题建立下述子载波对优化问题:

$\begin{matrix} \begin{matrix} \max_{α} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} α_{i, j} L_{i, j} + λ_{S} P_{T} + \overset{L}{\sum_{l = 1}} (μ_{1}^{l} + μ_{2}^{l}) I_{t h}^{l} \\ s . t . A 6 (25) \end{matrix} \end{matrix}$

式中: $\begin{matrix} L_{i, j} \end{matrix}$ 为 $\begin{matrix} K \times K \end{matrix}$ 阶矩阵,如下所示:

$\begin{matrix} L_{i, j} = [\begin{matrix} L_{1,1, m^{*}}^{*} & L_{1,2, m^{*}}^{*} & \dots & L_{1, K, m^{*}}^{*} \\ L_{2,1, m^{*}}^{*} & L_{2,2, m^{*}}^{*} & \dots & L_{2, K, m^{*}}^{*} \\ ⋮ & ⋮ & ⋮ \\ L_{K - 1,1, m^{*}}^{*} & L_{K - 1,2, m^{*}}^{*} & \dots & L_{K - 1, K, m^{*}}^{*} \\ L_{K, 1, m^{*}}^{*} & L_{K, 2, m^{*}}^{*} & \dots & L_{K, K, m^{*}}^{*} \end{matrix}] (26) \end{matrix}$

该矩阵可看作 $\begin{matrix} K \times K \end{matrix}$ 阶效益矩阵,每一行表示不同的工作者,每一列表示不同的任务,因此该线性分配问题等效为任务指派问题,对于上述子载波对匹配可用标准的匈牙利算法^{[ 14]}进行求解,算法复杂度为 $\begin{matrix} O (K^{3}) 。 \end{matrix}$

(4)次梯度迭代更新功率分配

次梯度迭代方法在保证收敛性的情况下得到最小对偶函数值。第 $\begin{matrix} n + 1 \end{matrix}$ 步迭代过程如下:

$\begin{matrix} \begin{matrix} λ_{S}^{(n + 1)} = λ_{S}^{(n)} - t_{1}^{(n)} [P_{T} - \overset{M}{\sum_{m = 1}} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} α_{i, j}^{*} β_{i, j, m^{*}} \cdot \\ (P_{i, j, m}^{1 *} + P_{i, j, m}^{2 *} + P_{i, j, m}^{3 *})] \\ μ_{1}^{l (n + 1)} = μ_{1}^{l (n)} - t_{2}^{(n)} [I_{t h}^{l} - \overset{M}{\sum_{m = 1}} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} α_{i, j}^{*} β_{i, j, m^{*}} \cdot \\ (P_{i, j, m}^{1 *} + P_{i, j, m}^{3 *} γ_{i, j, m}^{S}) I_{S, i}^{l}] \\ μ_{2}^{l (n + 1)} = μ_{2}^{l (n)} - t_{3}^{(n)} [I_{t h}^{l} - \overset{M}{\sum_{m = 1}} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} α_{i, j}^{*} β_{i, j, m^{*}} \cdot \\ (P_{i, j, m}^{2 *} I_{S, j}^{l} + γ_{i, j, m}^{R} P_{i, j, m^{*}}^{3 *} I_{R, j}^{l})] \\ (27) \end{matrix} \end{matrix}$

式中: $\begin{matrix} t_{1}^{(n)}, t_{2}^{(n)}, t_{3}^{(n)} \end{matrix}$ 为第 $\begin{matrix} n + 1 \end{matrix}$ 步迭代步长,本文采用递减步长^{[ 15]},即 $\begin{matrix} t_{k}^{(n)} = t_{k} / \sqrt[]{n}, k = [1,2, 3] 。 \end{matrix}$ 物理层优化问题简要步骤如下:

Step1 $\begin{matrix} n = 1, \end{matrix}$ 初始化乘子 $\begin{matrix} λ_{S}^{(1)} 、 μ_{1}^{(1)} 、 μ_{2}^{(1)}, \end{matrix}$ 初始迭代步长 $\begin{matrix} t_{k}, k = [1,2, 3], 迭代精度为 ε, 最大迭代次数为 N 。 \end{matrix}$

Step2 如果 $\begin{matrix} n \leq N, t_{k}^{(n)} = t_{k} / \sqrt[]{n} k = [1,2, 3] 。 \end{matrix}$

Step3 根据式(19),给定 $\begin{matrix} λ_{S}^{(n)}, μ_{1}^{(n)}, μ_{2}^{(n)} \end{matrix}$ 可求出 $\begin{matrix} P_{i, j, m}^{1}, P_{i, j, m}^{2}, P_{i, j, m}^{3}; \end{matrix}$ 把功率值代入式(20)(21)得参数 $\begin{matrix} ρ, \end{matrix}$ 根据式(24)得到子载波对最佳分配用户参数 $\begin{matrix} β, \end{matrix}$ 再根据式(25)(26)得到子载波对最佳匹配参数 $\begin{matrix} α 。 \end{matrix}$

Step4 将参数 $\begin{matrix} α 、 β \end{matrix}$ 代入式(27),更新乘子。

Step5 若乘子更新满足迭代精度要求,则迭代结束,输出结果。否则, $\begin{matrix} n = n + 1, \end{matrix}$ 返回Step2。

3.3 私有功率限制下的资源分配模型

优化模型P1限定中继和认知基站发送功率受限于总和功率阈值,但在实际中二者功率约束是相互独立的,则此时优化模型存在以下两种情况:

(1)当 $\begin{matrix} lo g_{2} (1 + γ_{i, R}^{S} P_{i, R}^{S}) \geq lo g_{2} (1 + γ_{i, m}^{S} P_{i, R}^{S} + γ_{j, m}^{R} P_{j, m}^{R}), 即 P_{j, m}^{R} \leq (γ_{i, R}^{S} - γ_{i, m}^{S}) P_{i, R}^{S} / γ_{j, m}^{R} \end{matrix}$ 时,目标速率为:

$\begin{matrix} \begin{matrix} R'_{m} = \frac{1}{2} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} α_{i, j} β_{i, j, m} \cdot \\ [ρ_{i, j, m} lo g_{2} (1 + γ_{i, m}^{S} P_{i, R}^{S} + γ_{j, m}^{R} P_{j, m}^{R}) + \\ (1 - ρ_{i, j, m}) R_{i, j, m}^{D}] \end{matrix} \end{matrix}$

(2)当 $\begin{matrix} lo g_{2} (1 + γ_{i, R}^{S} P_{i, R}^{S}) < lo g_{2} (1 + γ_{i, m}^{S} P_{i, R}^{S} + γ_{j, m}^{R} P_{j, m}^{R}), 即 P_{j, m}^{R} > (γ_{i, R}^{S} - γ_{i, m}^{S}) P_{i, R}^{S} / γ_{j, m}^{R} \end{matrix}$ 时,目标速率为:

$\begin{matrix} \begin{matrix} R ″_{m} = \frac{1}{2} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} α_{i, j} β_{i, j, m} [ρ_{i, j, m} lo g_{2} (1 + γ_{i, R}^{S} P_{i, R}^{S}) + \\ (1 - ρ_{i, j, m}) R_{i, j, m}^{D}] \end{matrix} \end{matrix}$

上述两个优化目标虽然不同,但在解优化问题时都以取等为界^{[ 10]}。因此,引入功率总和变量即 $\begin{matrix} P_{i, j, m}^{3} = P_{i, R}^{S} + P_{j, m}^{R}, \end{matrix}$ 结合式(5)(6)构建如下优化模型:

$\begin{matrix} \begin{matrix} P 3 : \max_{α, β, ρ, P} \overset{M}{\sum_{m = 1}} \ln (R_{m} - R_{m, \min}) \\ s . t . A 1 ~ A 7 \\ B 1 : \overset{M}{\sum_{m = 1}} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} (P_{i, j, m}^{1} + P_{i, j, m}^{2} + γ_{i, j, m}^{S} P_{i, j, m}^{3}) \leq P_{BS} \\ B 2 : \overset{M}{\sum_{m = 1}} \overset{K}{\sum_{i = 1}} \overset{K}{\sum_{j = 1}} γ_{i, j, m}^{R} P_{i, j, m}^{3} \leq P_{R} (28) \end{matrix} \end{matrix}$

优化模型P3对应的对偶问题如下:

$\begin{matrix} \begin{matrix} \min_{λ_{S}, λ_{R} \geq 0, μ_{1}, μ_{2} \geq 0} D (λ_{S}, λ_{R}, μ_{1}, μ_{2}) \\ s . t . A 6, A 7 (29) \end{matrix} \end{matrix}$

运用KKT条件可以求解该优化模型。每个用户在相应子载波对上的功率分配如下式:

$\begin{matrix} \{\begin{matrix} P_{i, j, m}^{1 *} = (1 - ρ_{i, j, m}) [w_{m} / 2 \ln 2 (λ_{S} + \\ {\overset{L}{\sum_{l = 1}} μ_{1}^{l} I_{S, i}^{l}) - 1 / γ_{i, m}^{S}]}^{+} \\ P_{i, j, m}^{2 *} = (1 - ρ_{i, j, m}) [w_{m} / 2 \ln 2 (λ_{S} + \\ {\overset{L}{\sum_{l = 1}} μ_{2}^{l} I_{S, j}^{l}) - 1 / γ_{j, m}^{S}]}^{+} \\ P_{i, j, m}^{3 *} = ρ_{i, j, m} [w_{m} / 2 \ln 2 (λ_{S} γ_{i, j, m}^{S} + λ_{S} γ_{i, j, m}^{R} + \\ \overset{L}{\sum_{l = 1}} μ_{1}^{l} I_{S, i}^{l} γ_{i, j, m}^{S} + \overset{L}{\sum_{l = 1}} μ_{2}^{l} I_{R, j}^{l} γ_{i, j, m}^{R}) - 1 / γ_{i, j, m}]^{+} \end{matrix} (30) \end{matrix}$

根据式(30)所求得的用户功率值,采用与模型P1相同的对偶分层求解方法,可决策私有功率约束下用户传输模式、载波配对、载波对分配,并通过次梯度迭代保证算法的收敛性能。

3.4 算法复杂度分析

物理层优化问题若采用耗尽搜索算法进行子载波配对和分配,则算法复杂度为 $\begin{matrix} O (2^{K} M^{K} K! TLK) \end{matrix}$ ,其中 $\begin{matrix} T \end{matrix}$ 为迭代次数, $\begin{matrix} K! \end{matrix}$ 为一个用户与子载波对匹配的可能,每一步迭代过程中有 $\begin{matrix} 2 L + 2 \end{matrix}$ 个变量,每一个子载波对上执行一次,所以约为 $\begin{matrix} LK \end{matrix}$ 。采用拉格朗日局部对偶求解算法,在每一步迭代过程中有 $\begin{matrix} 2 L + 2 \end{matrix}$ 个对偶乘子,在子载波匹配过程中采用匈牙利算法,据此分析,物理层算法复杂度为 $\begin{matrix} O (TL (M K^{2} + K^{3})) 。 \end{matrix}$ 应用层速率迭代更新次数为 $\begin{matrix} T' \end{matrix}$ ,整个算法复杂度为 $\begin{matrix} O (T' TL (M K^{2} + K^{3})) 。 \end{matrix}$

4 仿真结果分析

4.1 仿真环境及参数说明

认知基站、中继覆盖半径分别为1、0.5 km。认知簇小区内用户 $\begin{matrix} M \geq 4, \end{matrix}$ 认知中继和认知用户感知范围内的主用户数 $\begin{matrix} L = 4, \end{matrix}$ 其占用带宽分别为1、2、5、10 MHz,认知子载波带宽为0.3125 MHz。 $\begin{matrix} t \end{matrix}$ 时刻认知链路和干扰两节点间的信道增益为:

$\begin{matrix} h (t) = ρ (d) \cdot 10^{φ (t \frac{)}{10}} \cdot w (t) \end{matrix}$

式中: $\begin{matrix} ρ (d) \end{matrix}$ 为距离为 $\begin{matrix} d \end{matrix}$ 的两认知节点间的路径损耗,计算公式为 $\begin{matrix} 128.1 + 37.6 lo g_{10} d \end{matrix}$ (km); $\begin{matrix} 10^{φ (t \frac{)}{10}} \end{matrix}$ 为阴影衰落部分, $\begin{matrix} φ (t) \end{matrix}$ 为服从零均值、方差为 $\begin{matrix} σ_{φ}^{2} \end{matrix}$ =8 dB的正态分布; $\begin{matrix} w (t) \end{matrix}$ 为多径衰落信道增益部分,服从均值为 $\begin{matrix} μ_{w} = 1 \end{matrix}$ 的指数分布。噪声功率谱密度为-174 dBm/Hz。

4.2 仿真分析

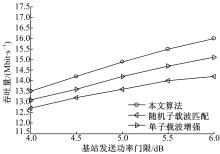
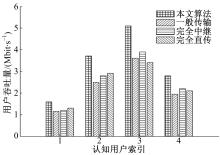
拟将本文所提出的增强传输算法与单子载波增强算法、随机子载波匹配算法进行性能对比。单子载波增强传输指两时隙采用相同子载波传输,子载波匹配参数 $\begin{matrix} α_{i, j} = \{\begin{matrix} 1, i = j \\ 0, i \neq j \end{matrix}, \end{matrix}$ 此时功率分配与本文提出算法相同。传输模式选择及子载波对分配与式(20)(21)(24)相同,进行最佳子载波分配的算法复杂度为 $\begin{matrix} (T' TLMK) 。 \end{matrix}$ 随机子载波匹配传输的资源分配过程与单子载波增强传输过程相同,复杂度也相同。

图2为 P_T=5 dB, $I_{th}^{l}$ =-140 dB, R_m_,min=1 Mbit/s, M=4时,本文提出的自适应增强传输与自适应一般传输、完全中继传输和完全直传时每一个用户吞吐量比较的柱状图。从图中可看出,本文提出增强传输模式下吞吐量要高于其他3种情况,增强传输相对于传统的一般传输在第二时隙有效利用空闲子载波,因此在基于中继协助的认知网络由于信道的时变特性,完全中继模式在某些时刻未必能提高网络的吞吐量,所以建立自适应选择机制既可以保证多用户传输需求,同时也可有效提高网络吞吐量。

	Figure Option View Download New Window
	图2 几种传输模式的用户吞吐量比较Fig.2 Comparision between the proposed mode and others

图3为 $\begin{matrix} I_{th}^{l} \end{matrix}$ =140 dB, R_m_,min=1 Mbit/s, M=4时系统吞吐量随总功率 $\begin{matrix} P_{T} \end{matrix}$ 变化的曲线,系统吞吐量随着发送总功率的增加而增加。但发送总功率值增加到5.5 dB时,吞吐量值趋于平缓,其原因是用户受到主用户旁瓣干扰限制。相比于单一子载波增强和两跳采用随机子载波配对这两种方法,本文算法显著提高了系统吞吐量。

	Figure Option View Download New Window
	图3 总发送功率受限下的吞吐量Fig.3 Thoughput under total transmission power constraint

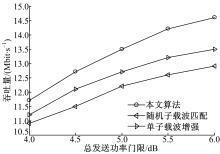
图4给出了目标效用随发送总功率增加的变化曲线,当发送总功率低于5 dB时,效用曲线变化明显是正数函数递增特性所致。

	Figure Option View Download New Window
	图4 总发送功率限制下目标效用值Fig.4 Object utilty under total transmission power constraint

图5为用户公平性随发送总功率增加的变化曲线。采用Jains提出的公平性因子来度量算法的公平性,用户公平性曲线随着发送功率的增加而降低,由于基于对数效用目标的影响在满足用户最低速率需求后,剩余资源分配到信道质量较好的用户,但在资源充足时非线性平滑增长,用户间速率差异不大。虽然基于子载波对的增强传输比其他两种传输策略公平性差异较小,但吞吐量却有明显提升。

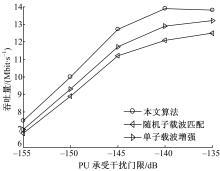
	Figure Option View Download New Window
	图5 总发送功率限制下的公平性Fig.5 The fairness under total transmission power constraint

图6为 P_T=5 dB, R_m_,min=1 Mbit/s, $\begin{matrix} M = \end{matrix}$ 4时在不同旁瓣干扰限制 $\begin{matrix} I_{t h}^{l} \end{matrix}$ 情况下的系统吞吐量曲线。在旁瓣干扰门限增加时,系统吞吐量值都在增加。但当干扰门限增大至-140 dB时,吞吐量值趋于平缓,此时受限于总发送功率。

	Figure Option View Download New Window
	图6 主用户旁瓣干扰限制下的吞吐量Fig.6 Thoughput under sidelobe interference constraint

图7为 P_R=0 dB, R_m_,min=1 Mbit/s, $\begin{matrix} M = 4 \end{matrix}$ 时,在不同基站发送功率门限 $\begin{matrix} P_{BS} \end{matrix}$ 值下的系统吞吐量变化曲线。当 $\begin{matrix} P_{BS} \end{matrix}$ 增加到一定程度时,系统受限于中继发送功率约束。若当私有功率限制总和等于总功率限制时,总功率限制下吞吐量高于私有限制,总功率限制资源分配是私有功率限制分配的理论上界值。

	Figure Option View Download New Window
	图7 私有发送限制下的吞吐量Fig.7 Thoughput under individual transmission power constraint

5 结束语

在认知多用户中继网络场景下,针对时变信道完全DF中继两跳传输的差异性问题,综合考虑用户速率需求及公平性采用纳什议价准则下的效用,提出分层优化模型的资源分配策略。运用局部对偶理论实现分层优化,并通过拉格朗日松弛算法求解用户功率分配,实现传输模式选择、载波配对、信道分配。仿真结果表明:相对于完全中继、直传网络和非载波配对的中继网络,本文所提算法可使系统吞吐量获得较大提升。但是基于纳什议价效用目标当频谱资源紧缺、功率严格受限或用户数较多时,优化模型无可行解,因此下一步将研究接入控制策略,在满足有限用户需求的同时使系统吞吐量得到提升。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Zhang Q, Jia J C, Zhang J. Cooperative relay to improve diversity in cognitive radio networks[J]. IEEE Communications Magazine, 2009, 47(2): 111-117. [本文引用:1] [JCR: 3.661]
[2]	Zou Y L, Zhu J, Zheng B Y, et al. An adaptive cooperation diversity scheme with best-relay selection in cognitive radio networks[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 5438-5445. [本文引用:1] [JCR: 2.813]
[3]	Bharadia D, Bansal G, Kaligineedi P, et al. Relay and power allocation schemes for OFDM-based cognitive radio systems[J]. IEEE Transactions on Wireless Communications, 2011, 10(9): 2812-2817. [本文引用:1] [JCR: 2.418]
[4]	Shaat M, Bader F. Asymptotically optimal resource allocation in OFDM-based cognitive networks with multiple relays[J]. IEEE Transactions on Wireless Communications, 2012, 11(3): 892-897. [本文引用:1] [JCR: 2.418]
[5]	Chen C H, Wang C L, Chen C T. A resource allocation scheme for cooperative multiuser OFDM-based cognitive radio systems[J]. IEEE Transactions on Wireless Communications, 2011, 59(11): 3204-3215. [本文引用:1] [JCR: 2.418]
[6]	Wang R, Lau V K N, Cui Y. Decentralized fair scheduling in two-hop relay-assisted cognitive OFDMA systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(1): 171-181. [本文引用:1]
[7]	Luan T X, Gao F F, Zhang X D. Joint resource scheduling for relay-assisted broadband cognitive radio network[J]. IEEE Transactions on Wireless Communications, 2012, 11(9): 3090-3100. [本文引用:1] [JCR: 2.418]
[8]	Zhao G D, Yang C Y, Li G Y, et al. Power and channel allocation for cooperative relay in cognitive radio networks[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(1): 151-159. [本文引用:1]
[9]	Liu Y, Chen W. Limited-feedback-based adaptive power allocation and subcarrier pairing for OFDM DF relay networks with diversity[J]. IEEE Transactions on Vehicular Technology, 2012, 61(6): 2559-2571. [本文引用:1] [JCR: 2.063]
[10]	Attar A, Nakhai M R, Aghvami A H. Cognitive radio game for secondary spectrum access problem[J]. IEEE Transactions on Wireless Communications, 2009, 8(4): 2121-2131. [本文引用:2] [JCR: 2.418]
[11]	Ngo D T, Le-Ngoc T. Distributed resource allocation for cognitive radio networks with spectrum-sharing constraints[J]. IEEE Transactions on Vehicular Technology, 2011, 60(7): 3436-3449. [本文引用:1] [JCR: 2.063]
[12]	Yu W, Lui R. Dual methods for non-convex spectrum optimization of multicarrier systems[J]. IEEE Transactions on Communications, 2006, 54(7): 1310-1322. [本文引用:1] [JCR: 1.75]
[13]	Ng T C Y, Yu W. Joint optimization of relay strategies and resource allocations in cooperative cellular networks[J]. IEEE Journal on Selected Areas in Communications, 2007, 25(2): 328-339. [本文引用:1] [JCR: 3.121]
[14]	Kuhn H W. The Hungarian method for the assignment problem[J]. Naval Research Logistics Quarterly, 1955, 2(1/2): 83-97. [本文引用:1]
[15]	Tao M X, Liang Y C, Zhang F. Resource allocation for delay differentiated traffic in multiuser OFDM systems[J]. IEEE Transactions on Wireless Communications, 2008, 7(6): 2190-2201. [本文引用:1] [JCR: 2.418]

2009

3.661

0.0

... 然而频谱感知并非完美,会对主用户带来较大干扰,阻碍动态频谱接入技术的应用,引入认知中继后既可以改善链路质量,也可以降低发送功率,即降低对主用户网络的干扰,增强网络覆盖^[1],因此研究这种情况下的资源分配问题显得尤为重要 ...

2010

2.813

0.0

... 针对单用户的资源分配主要是通过合理的调度机制^[2]和最优化理论^[3,4]实现点对点系统中继选择或中继分配、载波分配和功率分配等 ...

2011

2.418

0.0

... 针对单用户的资源分配主要是通过合理的调度机制^[2]和最优化理论^[3,4]实现点对点系统中继选择或中继分配、载波分配和功率分配等 ...

2012

2.418

0.0

... 针对单用户的资源分配主要是通过合理的调度机制^[2]和最优化理论^[3,4]实现点对点系统中继选择或中继分配、载波分配和功率分配等 ...

2011

2.418

0.0

2011

0.0

2012

2.418

0.0

2011

0.0

... 自适应选择传输模式在单用户场景^[8]得到广泛研究,但不能简单应用到多用户竞争场景,且难以确保用户的QoS及用户公平性 ...

2012

2.063

0.0

... 其次,中继两跳采用相同子载波时,存在两跳传输差异问题,通过子载波配对技术可解决该问题^[9] ...

2009

2.418

0.0

... 基于上述分析,本文基于多个主用户共存下的认知下行OFDMA系统场景,提出自适应选择中继协助策略,为兼顾用户公平性及用户的速率需求,采用纳什议价公平性准则效用函数作为优化目标^[10],为求解该优化模型,提出分层分配框架,应用层根据当前信道状况自适应调整不同用户速率需求,物理层采用子载波对技术,自适应实现资源最佳分配 ...

... 上述两个优化目标虽然不同,但在解优化问题时都以取等为界^[10] ...

2011

2.063

0.0

... 假设认知用户完美感知接入,认知用户采用OFDM调制,而主用户采用非正交调制,认知用户会对主用户带来旁瓣干扰^[11] ...

2006

1.75

0.0

... 由于该优化模型非凸特性,运用对偶理论求解存在对偶间隙,但系统子载波数足够大时,通过对偶虚拟近似存在零对偶差异^[12] ...

2007

3.121

0.0

... 上述对偶问题可通过次梯度迭代更新乘子 w求解^[13] ...

1955

0.0

. 1955, 2(1‐2):83-97

The Hungarian method for the assignment problem

H. W. Kuhn

Bryn Mawr College

> Assuming that numerical scores are available for the performance of each of n persons on each of n jobs, the “assignment problem” is the quest for an assignment of persons to jobs so that the sum of the n scores so obtained is as large as possible. It is shown that ideas latent in the work of two Hungarian mathematicians may be exploited to yield a new method of solving this problem.

... 该矩阵可看作 K×K阶效益矩阵,每一行表示不同的工作者,每一列表示不同的任务,因此该线性分配问题等效为任务指派问题,对于上述子载波对匹配可用标准的匈牙利算法^[14]进行求解,算法复杂度为 O(K3) ...

2008

2.418

0.0

... 式中: t1(n),t2(n),t3(n)为第 n+1步迭代步长,本文采用递减步长^[15],即 tk(n)=tk/n,k=[1,2,3] ...