基于指数熵的认知无线电频谱感知算法

引用本文

李一兵, 常国彬, 叶方. 基于指数熵的认知无线电频谱感知算法. 吉林大学学报:工学版, 2014, 44(5): 1506-1511[LI Yi-bing, CHANG Guo-bin, YE Fang. Exponential entropy-based spectrum sensing algorithm in cognitive radio. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1506-1511] 复制到剪切板

Permissions

基于指数熵的认知无线电频谱感知算法

李一兵, 常国彬, 叶方

哈尔滨工程大学信息与通信工程学院, 哈尔滨 150001

通信作者:叶方（1980-）,女,副教授,硕士生导师.研究方向:认知无线电,LTE系统干扰抑制. E-mail:yefang0815@sina.cn

作者简介:李一兵（1967-）,男,教授,博士生导师.研究方向:认知无线电.E-mail:liyibing0920@sina.cn

基金:黑龙江省青年科学基金项目（QC2012C070）

摘要

针对目前认知无线电中频谱感知技术在低信噪比下检测性能差、对噪声功率不确定性鲁棒性差等问题,提出了一种基于指数熵的频谱感知算法。该方法根据H₀、H₁下接收信号熵特性的不同,估计接收信号的指数熵,然后通过与预设的门限进行比较,进而判断主用户信号是否存在。该方法的主要优点为:具有对噪声功率不确定性具有鲁棒性、不需要信号的先验知识以及在低信噪比下可以得到较高的检测概率。Monte Carlo仿真结果表明:在噪声功率不确定性为3 dB,采样点数为1024的情况下,当信噪比大于-8 dB时,可以达到100%的检测概率。

关键词: 通信技术; 频谱感知; 指数熵; 鲁棒性

中图分类号:TN92 文献标志码:A 文章编号:1671-5497(2014)05-1506-06

Exponential entropy-based spectrum sensing algorithm in cognitive radio

LI Yi-bing, CHANG Guo-bin, YE Fang

College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001

Abstract

Current spectrum sensing methods in cognitive radio possess several shortcomings, such as poor detection performance in low Signal-to-Noise Ratio (SNR) simulation and poor robustness to the uncertainty of noise power, etc. To overcome these shortcomings, an exponential entropy-based spectrum sensing algorithm is proposed. According to the difference of exponential entropy between the situation ofH₀ andH₁, the value of the exponential entropy of the received signal is estimated, and then compared with the threshold to judge whether the primary user's signal exists or not. The algorithm has the advantages of robustness to uncertainty of noise power, no requirement of prior information of the primary user's signal, and high detection probability in low SNR, etc. Monte Carlo simulation results show that under the situation of noise power uncertainty of 3 dB, sampling number of 1024, the detection probability can reach 100% when SNR is higher than -8 dB.

Keyword: communication technology; spectrum sensing; exponential entropy; robustness

Show Figures

0 引言

随着无线通信业务的发展,频谱资源变得日益稀缺。原有固定的频谱分配制度将难以满足日益增长的频谱需求。然而,根据美国联邦通信委员会(FCC)的研究报告^{[ 1, 2]},频谱使用率随时间、地区和频段的不同而不同,在15%~85%内取值。认知无线电是针对这一问题应运而生的新技术^{[ 3]}。通过对频谱资源的动态分配,使得认知用户在授权用户不占用授权频段的情况下利用该频段,从而提高了频谱利用率^{[ 4, 5]}。频谱感知(频谱检测)是认知无线电的关键技术之一,它的主要功能在于检测可供未授权用户使用的频谱空穴,同时检测授权用户对该频段的使用情况,使得当授权用户再次使用该频段时认知用户马上退出,保证不干扰授权用户通信。

传统的频谱感知算法有匹配滤波器检测、能量检测、循环平稳特征检测等方法^{[ 6, 7]}。匹配滤波器算法从最大信噪比出发,感知实时性较好,是一种最优的频谱检测算法,但是需要授权用户信号的先验信息。循环平稳特征检测具有较高的信号辨识能力,但是算法复杂度较高,实时性较差。能量检测无需信号的先验信息,复杂度低,在噪声功率确定的情况下,是一种快速有效的盲检测算法,但是对噪声功率的不确定性非常敏感,鲁棒性很差。为了提高检测性能的抗噪声不确定性能力,文献[8-10]提出了基于香农熵的频谱感知算法。但是该算法在计算过程中很容易出现不收敛的现象,造成无效检测。本文将指数熵的概念引入到频谱检测当中,保留了对噪声功率不确定的鲁棒性,同时又有效地避免了无效检测情况的出现。通过仿真实验对本文提出的指数熵的检测算法(Exponential entropy-based detection,EED)进行了详尽分析,并与香农熵检测算法(Shannon entropy-based detection,SED)和能量检测算法(Energy detection,ED)在噪声功率不确定时的检测性能进行了比较。

1 信号的频域分析

在认知无线电系统中,可以把频谱感知归结为一个二元检测的问题:

$\begin{matrix} x (n) = \{\begin{matrix} H_{0} : w (n), n = 0,1, \dots, N - 1 \\ H_{1} : s (n) + w (n), n = 0,1, \dots, N - 1 \end{matrix} (1) \end{matrix}$

式中: $\begin{matrix} s (n) \end{matrix}$ 为授权用户信号; $\begin{matrix} w (n) \end{matrix}$ 为高斯白噪声; $\begin{matrix} H_{0} / H_{1} \end{matrix}$ 代表频段空闲/被占用。

对式(1)进行傅里叶变换,得到:

$\begin{matrix} \vec{X} (k) = \{\begin{matrix} H_{0} : \vec{W} (k), k = 0,1, \dots, N - 1 \\ H_{1} : \vec{S} (k) + \vec{W} (k), k = 0,1, \dots, N - 1 \end{matrix} (2) \end{matrix}$

式中: $\begin{matrix} \vec{X} (k) 、 \vec{S} (k) \end{matrix}$ 和 $\begin{matrix} \vec{W} (k) \end{matrix}$ 分别代表接收信号、授权用户信号以及噪声的复频率谱。

$\begin{matrix} \begin{matrix} \vec{X} (k) = X_{r} (k) + j X_{i} (k) = \\ \frac{1}{N} \overset{N - 1}{\sum_{n = 0}} x (n) \exp (- j \frac{2 π}{N} kn) (3) \\ k = 0,1, \dots, N - 1 \end{matrix} \end{matrix}$

由于 $\begin{matrix} w (n) \end{matrix}$ 是独立同分布服从高斯分布的随机变量,因此噪声复频谱的实部和虚部 $\begin{matrix} W_{r} (k) 、 W_{i} (k) \end{matrix}$ 也是服从高斯分布的随机变量^{[ 10]}:

$\begin{matrix} W_{r} (k) ~ N (0, \frac{σ_{0}^{2}}{2 N}); W_{i} (k) ~ N (0, \frac{σ_{0}^{2}}{2 N}) (4) \end{matrix}$

因此,在假设 $\begin{matrix} H_{0} \end{matrix}$ 下噪声复频谱的幅值 $\begin{matrix} W (k) \end{matrix}$ 服从参数为 $\begin{matrix} σ_{0}^{2} / (2 N) \end{matrix}$ 的瑞利分布。

在假设 $\begin{matrix} H_{1} \end{matrix}$ 下,接收信号包括授权用户信号和噪声。此时接收信号复频谱的实部和虚部都服从如下的高斯分布:

$\begin{matrix} X_{r} (k) ~ N (S_{r} (k), \frac{σ_{0}^{2}}{2 N}); X_{i} (k) ~ N (S_{i} (k), \frac{σ_{0}^{2}}{2 N}) (5) \end{matrix}$

一般地,对于载荷信息的授权用户信号,复频谱的实部和虚部都不为0,因此在假设 $\begin{matrix} H_{1} \end{matrix}$ 下复频谱的幅值 $\begin{matrix} X (k) \end{matrix}$ 服从莱斯分布。由于莱斯分布的熵与瑞利分布的熵不同,因此可以根据信息熵来进行授权用户信号检测。

2 基于指数熵的频谱检测算法

2.1 基于香农熵的频谱检测算法

香农熵用来衡量信息平均不确定性的大小。一个系统越有序,香农熵就越低,反之,一个系统越是混乱,香农熵就越高。对于一个样本空间为 $\begin{matrix} [x_{1}, x_{2}, \dots, x_{L}] \end{matrix}$ 的离散随机变量 $\begin{matrix} X \end{matrix}$ 来说,其香农熵为:

$\begin{matrix} H (X) = E [lo g_{2} \frac{1}{P (x_{i})}] = - \overset{L}{\sum_{i = 1}} P (x_{i}) lo g_{2} P (x_{i}) (6) \end{matrix}$

文献[8-10]提出了基于香农熵的频谱检测算法,利用香农熵的估计值作为判决统计量来确定主用户信号是否存在。判决规则为:

$\begin{matrix} {\hat{H}}_{SHAN} (X) = - \overset{L}{\sum_{j = 1}} \frac{k_{j}}{N} lo g_{2} (\frac{k_{j}}{N}) \{\begin{matrix} \leq λ ∶ H_{1} \\ > λ ∶ H_{0} \end{matrix} (7) \end{matrix}$

式中: $\begin{matrix} k_{j} \end{matrix}$ 为落在第 $\begin{matrix} j \end{matrix}$ 个区间的观测值个数; $\begin{matrix} L \end{matrix}$ 为分段数目。

通过一系列复杂的数学推导^{[ 8, 9]},可以得到 $\begin{matrix} H_{0} \end{matrix}$ 下香农熵的估计值:

$\begin{matrix} H_{SHAN} (X) = \ln (\frac{L}{C_{1} \sqrt[]{2}}) + \frac{γ}{2} + 1 (8) \end{matrix}$

式中: $\begin{matrix} C_{1} \end{matrix}$ 和 $\begin{matrix} γ \end{matrix}$ 均为常数; $\begin{matrix} H_{SHAN} (X) \end{matrix}$ 只与分段数目 $\begin{matrix} L \end{matrix}$ 有关,与噪声功率无关。

噪声功率的不确定性影响检测性能主要是因为虚警概率即 $\begin{matrix} P_{f} = P (H_{1} | H_{0}) \end{matrix}$ 对其非常敏感,因此该方法克服了噪声功率不确定性对检测性能所造成的影响。

2.2 香农熵的频谱检测算法存在的问题

香农熵在解决实际问题时存在一定的缺陷。在香农熵的定义中,如果事件 $\begin{matrix} x_{i} \end{matrix}$ 出现的概率趋近于0,按照定义,信息熵的增量 $\begin{matrix} ΔI (P_{i} = 0) = lo g_{2} (\frac{1}{P_{i}}) \end{matrix}$ 趋于¥,所以尽管通过式(8)可以得到 $\begin{matrix} X \end{matrix}$ 的香农熵估计值在 $\begin{matrix} L \end{matrix}$ 一定的情况下是一个固定值,然而在实际对香农熵进行估计计算的过程中,很容易出现不收敛的情况,即 $\begin{matrix} k_{i} = 0, lo g_{2} (\frac{k_{i}}{N}) = - \infty \end{matrix}$ 而导致本次检测失效。在信号采样、变换等工作都完成后,若不能有效地对信号存在情况做出判断,将必然导致资源的浪费以及系统时效性和检测效率的降低。

2.3 基于指数熵的频谱检测算法

2.3.1 指数熵的提出

为了解决基于香农熵的频谱检测算法的检测失效问题,本文将指数熵的概念引入到检测算法中。通过下面的定义可以发现,指数熵增量在概率为0时其值为0,因此在估计计算的过程中不存在不收敛的现象,也就是完全避免了检测失效的现象。

指数熵是基于以下原则定义的^{[ 11]}:

(1)设每个状态 $\begin{matrix} x_{i} \end{matrix}$ 出现的概率为 $\begin{matrix} P_{i}, \end{matrix}$ 则其所携带的信息量 $\begin{matrix} ΔI (P_{i}) \end{matrix}$ 在 $\begin{matrix} [0,1] \end{matrix}$ 之间的所有点都有定义。

(2) $\begin{matrix} \lim_{P_{i} \to 0} ΔI (P_{i}) = ΔI (P_{i} = 0) = k_{1}, k_{1} \geq 0 \end{matrix}$ 且有限。

(3) $\begin{matrix} ΔI (P_{i} = 1) = k_{2}, k_{2} \geq 0 \end{matrix}$ 且有限。

(4) $\begin{matrix} k_{2} < k_{1} 。 \end{matrix}$

(5)随着 $\begin{matrix} P_{i} \end{matrix}$ 的增大, $\begin{matrix} ΔI (P_{i}) \end{matrix}$ 呈指数形式减少。

(6) $\begin{matrix} ΔI (P_{i}) \end{matrix}$ 和熵 $\begin{matrix} H \end{matrix}$ 在 $\begin{matrix} [0,1] \end{matrix}$ 上是连续的。

(7)当 $\begin{matrix} P_{i} (i = 1,2, \dots, n) \end{matrix}$ 相等时,熵 $\begin{matrix} H \end{matrix}$ 取最大值。

为了满足以上7个原则,指数熵被定义为:

$\begin{matrix} H_{EXP} = \overset{n}{\sum_{i = 1}} P_{i} e^{(1 - P_{i})} (9) \end{matrix}$

指数熵的提出有效规避了用对数定义信息熵中的无定义值和零值的问题,克服了香农熵的不足。将指数熵应用到频谱检测中来,巧妙地解决了2.2节中提到的检测失效问题。而且,指数运算相对对数运算较快,检测的时效性也可以得到提升。

2.3.2 算法流程

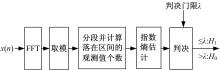
基于指数熵的频谱检测算法系统框图如图1所示。具体过程如下:

(1)对接收信号 $\begin{matrix} x (n) \end{matrix}$ 进行傅里叶变换,得到接收信号的复频谱 $\begin{matrix} \vec{X} = FFT [x (n)] 。 \end{matrix}$

(2)取其幅值 $\begin{matrix} X = |\vec{X}| = \sqrt[]{X_{r}^{2} (k) + X_{i}^{2} (k)} \end{matrix}$ 作为观测值。

(3)令 $\begin{matrix} X_{\max} 、 X_{\min} \end{matrix}$ 分别代表观测值 $\begin{matrix} X \end{matrix}$ 的最大值和最小值,将范围 $\begin{matrix} [X_{\min}, X_{\max}] \end{matrix}$ 分为 $\begin{matrix} L \end{matrix}$ 个区间,分段间隔满足 $\begin{matrix} Δ = \frac{X_{\max} - X_{\min}}{L}, \end{matrix}$ 然后计算表示落在第 $\begin{matrix} j \end{matrix}$ 个区间的观测值个数 $\begin{matrix} k_{j} \end{matrix}$ 。

(4)估计 $\begin{matrix} X \end{matrix}$ 的指数熵:

$\begin{matrix} {\hat{H}}_{EXP} (X) = \overset{L}{\sum_{j = 1}} \frac{k_{j}}{N} e^{(1 - \frac{k_{j}}{N})} (10) \end{matrix}$

(5)通过式(8)计算的指数熵估计值与门限比较,判断授权用户信号是否存在。判决规则为:

$\begin{matrix} {\hat{H}}_{EXP} (X) = \overset{L}{\sum_{j = 1}} \frac{k_{j}}{N} e^{(1 - \frac{k_{j}}{N})} \{\begin{matrix} \leq λ ∶ H_{1} \\ > λ ∶ H_{0} \end{matrix} (11) \end{matrix}$

指数熵估计值 $\begin{matrix} {\hat{H}}_{EXP} (X) \end{matrix}$ 与香农熵估计值 $\begin{matrix} {\hat{H}}_{SHAN} (X) \end{matrix}$ 具有相似的性质。式(8)表明, $\begin{matrix} X \end{matrix}$ 的香农熵估计值与噪声功率无关,且是分段数目 $\begin{matrix} L \end{matrix}$ 的增函数。事实上, $\begin{matrix} X \end{matrix}$ 的指数熵估计值与噪声功率大小也是无关的,说明基于指数熵的频谱检测算法对噪声功率的不确定性也有鲁棒性。而且指数熵估计值也是分段数目 $\begin{matrix} L \end{matrix}$ 的增函数。这两点可以通过第3节的仿真实验证明。

	Figure Option View Download New Window
	图1 指数熵检测系统框图Fig.1 System chart of exponential entropy-based detection

2.3.3 判决门限的确定

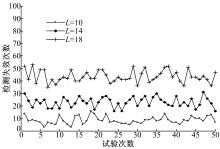
在采样点数 $\begin{matrix} N \end{matrix}$ 和实验分段数 $\begin{matrix} L \end{matrix}$ 确定时,指数熵的估计值就可以确定。再根据系统虚警概率的要求,式(11)中的门限值 $\begin{matrix} λ \end{matrix}$ 即可确定。门限越高,主用户信号的检测概率和虚警概率越高,反之亦然。具体应根据系统对检测概率和虚警概率的要求而定。

3 仿真实现及分析

图2是对基于香农熵检测失效情况的一个仿真实验。实验分为3组,每组独立实验50次,每次又进行100次检测。实验中接收信号是高斯白噪声,采样点数 $\begin{matrix} N = 512, \end{matrix}$ 三组实验分段数分别为 $\begin{matrix} L = 10,14,18 。 \end{matrix}$ 通过图2可以看出,每组实验的100次实验都有存在失效检测,而且随着分段数的增加,失效次数明显增加,这是由于当 $\begin{matrix} L \end{matrix}$ 增加时,分段区间的长度 $\begin{matrix} Δ \end{matrix}$ 变小,落在 $\begin{matrix} iΔ \end{matrix}$ 区间的检测值个数 $\begin{matrix} k_{i} \end{matrix}$ 为0的概率变大。当分段数为18时,平均失效比例达到40%以上。

	Figure Option View Download New Window
	图2 香农熵检测法检测失效实验Fig.2 Detection failure experiment of Shannon entropy-based detection method

图3给出了噪声功率与指数熵估计值之间的关系,噪声序列长度 $\begin{matrix} N = 512 。 \end{matrix}$ 可以看出,与香农熵一样,采样值的指数熵估计值也是不随着噪声功率的变化而变化的。也就是说,基于指数熵的频谱检测算法对噪声功率不确定性具有鲁棒性。

	Figure Option View Download New Window
	图3 噪声功率对指数熵估计值的影响Fig.3 Effect of noise power on the exponential entropy’s estimated value

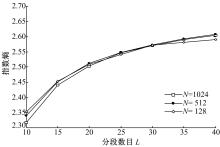从图3中两条曲线的对比以及图4曲线的变化趋势可以看出,指数熵的估计值是随着分段数目的增加而变大的。从图4还可以看出,指数熵估计值随着采样点数 $\begin{matrix} N \end{matrix}$ 的增加略有减小,所以当门限确定以后,采样点数的变化对虚警概率的影响很小。

	Figure Option View Download New Window
	图4 H₀下分段数目对指数熵估计值的影响Fig.4 Effect of bin number L on the exponential entropy’s estimated value under H₀

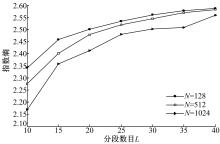图5给出了当主用户信号存在,信噪比为-10 dB时指数熵估计值与分段数目的关系。本文仿真中所有主用户信号均为BPSK信号,码元速率为 $\begin{matrix} R_{b} = 8 kbit / s, \end{matrix}$ 载波频率为 $\begin{matrix} f_{c} = 16 kHz, \end{matrix}$ 采样频率为 $\begin{matrix} f_{s} = 256 kHz 。 \end{matrix}$ 可以看出,指数熵估计值随着 $\begin{matrix} L \end{matrix}$ 的增加而变大。对比3条曲线还可以看出,随着采样点数的增加,熵值减小,而且不同于 $\begin{matrix} H_{0} \end{matrix}$ 条件下,此时的变化是比较明显的。说明当门限确定以后,检测概率随着采样点数的增加将有明显提高。通过图4、图5的指数熵估计值大小对比还可以看出, $\begin{matrix} H_{1} \end{matrix}$ 下的值小于 $\begin{matrix} H_{0} \end{matrix}$ 下的值,说明了判决规则即式(11)的合理性。

	Figure Option View Download New Window
	图5 H₁下分段数目对指数熵估计值的影响Fig.5 Effect of bin number L on the exponential entropy’s estimated value under H₁

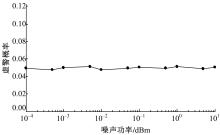
图6为虚警概率与噪声功率之间的关系。仿真实验中信号采样点数 $\begin{matrix} N = 512 \end{matrix}$ ,分段数 $\begin{matrix} L = 20, \end{matrix}$ 门限 $\begin{matrix} λ \end{matrix}$ 按照噪声功率为1、虚警概率为0.05时设定。门限设定以后通过改变噪声功率来分析噪声功率不确定性对虚警概率的影响。实验中采用Monte carlo法,独立实验10 000次。通过仿真实验结果可以发现,虚警概率基本保持在0.05,不随着噪声功率的变化而变化。从而又一次说明了基于指数熵的检测算法不会受到噪声功率不确定性的影响,具有较强的鲁棒性。

	Figure Option View Download New Window
	图6 噪声功率对虚警概率的影响Fig.6 Effect of noise power on false alarm probability

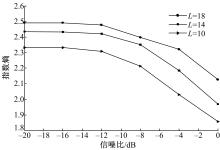
图7为有授权用户信号存在下的指数熵与信噪比的变化关系。可以看出,随着信噪比的增加,指数熵越来越小。所以当判决门限确定后,检测概率将随着信噪比的增加而提高。同时还可以看出,随着分段数目的增加,指数熵变大,这与从图3、图5得到的结论是一致的。

	Figure Option View Download New Window
	图7 指数熵估计值与信噪比的关系Fig.7 Relationship between exponential entropy’s estimated value of and SNR

图8给出了基于指数熵(EED)的频谱检测算法与基于香农熵(SED)的频谱检测算法和能量检测算法(ED)在噪声功率不确定情况下的检测性能对比。仿真中采用Monte carlo法,仿真次数为10 000次。采样点数分别为1024、512,分段数 $\begin{matrix} L = 20 \end{matrix}$ ,噪声功率不确定度 $\begin{matrix} ρ = 3 dB \end{matrix}$ ,分别选择合适的门限使 $\begin{matrix} P_{f} \end{matrix}$ 保持在0.1。在统计香农熵检测算法的检测概率时,若本次检测失效,由于无法对主用户信号是否存在做出判决,所以香农熵检测法的检测概率应该定义为: $\begin{matrix} P_{d} = N_{Dec} / (N_{Tal} - N_{Fail}) | H_{1}, \end{matrix}$ 虚警概率应该定义为: $\begin{matrix} P_{f} = N_{Dec} / (N_{Tal} - N_{Fail}) | H_{0} \end{matrix}$ ,其中 $\begin{matrix} N_{Dec} \end{matrix}$ 为判决主用户信号存在的次数, $\begin{matrix} N_{Tal} \end{matrix}$ 为总的实验次数, $\begin{matrix} N_{Fail} \end{matrix}$ 为失效检测次数。从图8可以看出,EED的检测性能优于SED,二者在噪声功率不确定情况下的检测性能都明显优于ED,即对噪声功率不确定性都具有鲁棒性,但是EED可以克服SED检测失效的问题,提高了检测效率。

	Figure Option View Download New Window
	图8 噪声功率不确定条件下指数熵检测与香农熵检测和能量检测检测性能对比Fig.8 Comparison of detection performance between EED and SED,ED in the situation of noise power uncertain

当 $\begin{matrix} N = 1024 \end{matrix}$ 时,EED在信噪比为-8 dB时的检测概率为1,达到了最优检测,而此时ED的检测概率几乎为0。当信噪比约为-5 dB时,ED才达到最优检测,说明EED在低信噪比下有较好的抗噪声功率不确定性能力,采样点数 $\begin{matrix} N = 512 \end{matrix}$ 时的曲线也说明了这一点。通过图8还可以看出,随着采样点数的增加,EED在低信噪比下的检测性能也得到了提高,但这是以检测的时效性为代价的。

4 结束语

噪声功率的不确定性是限制频谱感知性能的主要因素之一。基于香农熵的频谱感知算法对噪声功率不确定性具有鲁棒性,但是在实际对香农熵进行估计计算时,容易出现不收敛的情况,进而造成检测失效的现象。为此本文引入指数熵的概念,既保留了香农熵检测鲁棒性的优点,又有效地避免了检测失效的问题。仿真结果显示,虚警概率随着噪声功率的变化基本保持恒定,说明基于指数熵的频谱感知算法对噪声功率不确定性也具有鲁棒性。通过与能量检测法在噪声功率波动情况下检测性能的对比,再一次说明提出的基于指数熵的频谱检测算法在低信噪比下具有很好的抗噪声功率不确定的能力。另外,随着采样点数的增加,检测性能得到了提高,但这是以牺牲时效性为代价的,实际中需要在检测性能与时效性之间进行权衡。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	FCC. reporting of the spectrum efficiency working group[R/OL]. [2012-11-05]. Spectrum Policy Task Force, 2002. http:www.fcc.gov/sptf/reports/html. [本文引用:1]
[2]	Fu S, Li Y B, Ye F. spectrum sensing technology defending against SNR attack based on geographic location information[J]. Journal of Information and Computational Science, 2012, 9(13): 3721-3729. [本文引用:1]
[3]	Mchenry M. Report on spectrum occupancy measurements[R]. Shared Spectrum Company Report, Virginia, 2005. [本文引用:1]
[4]	Mitola J, Maguire G Q. Cognitive radio: aking software radios more personal[J]. IEEE Personal Communications, 1999, 6(4): 13-18. [本文引用:1]
[5]	Haykin S. Cognitive radio: brain-empowered wireless communications[J]. IEEE Sel Areas Commun, 2005, 23: 201-220. [本文引用:1] [JCR: 3.121]
[6]	李文生, 李一兵. 一种认知无线电频谱检测新算法[J]. 应用科技, 2011, 38(1): 49-52. Li Wen-sheng, Li Yi-bing. A new algorithm for spectrum detection in cognitive radio system[J]. Applied Science and Technology, 2011, 38(1): 49-52. [本文引用:1] [CJCR: 0.3826]
[7]	赵春晖, 腾志军, 马爽. 基于广义功率谱密度的分布压缩宽带频谱感知[J]. 吉林大学学报: 工学版, 2012, 42(4): 1015-1020. Zhao Chun-hui, Teng Zhi-jun, Ma Shuang. Distributed compressive wideband spectrum sensing based on generalized power density[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(4): 1015-1020. [本文引用:1] [CJCR: 0.701]
[8]	Zhang Ya-lin, Zhang Qin-yu, Melodia Tommaso. A frequency-domain entropy-based detector for robust spectrum sensing in cognitive radio networks[J]. Communications Letters, IEEE, 2010, 14: 533-535. [本文引用:1] [JCR: 1.16]
[9]	Zhang Ya-lin, Zhang Qin-yu, Wu Shao-hua. Entropy-based robust spectrum sensing in cognitive radio[J]. Communications, IET, 2010, 4(4): 428-436. [本文引用:1] [JCR: 0.637]
[10]	Sabat Samrat L, Srinu S, Raveendranadh A, et al. Spectrum sensing based on entropy estimation using cyclostationary features for Cognitive radio[C]∥Communication Systems and Networks. 2012 Fourth International Conference on, Bangalore, 2012: 1-6. [本文引用:1]
[11]	潘喆, 吴一全. 二维指数熵图像阈值选取方法及其快速算法[J]. 计算机应用, 2007, 27(4): 982-985. Pan Zhe, Wu Yi-quan. Method of thresholding using two-dimensional exponential entropy and its fast algorithm[J]. Computer Applications, 2007, 27(4): 982-985. [本文引用:1] [CJCR: 0.1916]

2012

0.0

... 然而,根据美国联邦通信委员会(FCC)的研究报告^[1,2],频谱使用率随时间、地区和频段的不同而不同,在15%~85%内取值 ...

2012

0.0

... 然而,根据美国联邦通信委员会(FCC)的研究报告^[1,2],频谱使用率随时间、地区和频段的不同而不同,在15%~85%内取值 ...

2005

0.0

... 认知无线电是针对这一问题应运而生的新技术^[3] ...

1999

0.0

... 通过对频谱资源的动态分配,使得认知用户在授权用户不占用授权频段的情况下利用该频段,从而提高了频谱利用率^[4,5] ...

2005

3.121

0.0

... 通过对频谱资源的动态分配,使得认知用户在授权用户不占用授权频段的情况下利用该频段,从而提高了频谱利用率^[4,5] ...

2011

0.0

0.3826

. 2011, 38(1):49-52

A new algorithm for spectrum detection in cognitive radio system

认知无线电(cognitive radio, CR)是一种革命性智能频谱共享技术,可显著提高频谱使用率.该文提出一种基于似然比判决的协同频谱检测算法用于多用户认知无线电系统的主用户检测.该算法特别考虑了主用户和多个认知用户之间不同的信道衰落和路径衰减状况,并根据最优的似然比判决法组建数学模型,保证了检测算法的高度精确性.随后,对相关参数进行了合理简化,降低了算法复杂性.实验表明,该文算法拥有非常高的检测精度,复杂度也不高,能够更加有效地服务于实际的认知无线电系统.

... 传统的频谱感知算法有匹配滤波器检测、能量检测、循环平稳特征检测等方法^[6,7] ...

2012

0.0

0.701

. 2012, 42(4):1015-1020

Distributed compressive wideband spectrum sensing based on generalized power density

College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China

In order to achieve wideband spectrum sensing under Alpha stable noise, generalized power spectrum density is proposed, based on which the distributed compressive wideband spectrum sensing is put forward. This method can effectively restrain the Alpha stable noise. First, the received wideband signal is processed by fractional lower order, then, the autocorrelation vectors are calculated. Combined with the compressed sensing theory, the fractional generalized power spectrum density is derived by Fourier transform. Simulation results show that the method performs well in the estimation of the wideband power spectrum density, and can achieve wideband spectrum sensing under Alpha stable noise.

为实现在Alpha稳定分布噪声下宽带频谱感知,扩展了传统功率谱密度概念,提出广义功率谱密度的概念,在此基础上提出基于广义功率谱密度的分布压缩宽带频谱感知。此方法能有效地抑制Alpha稳定分布噪声。首先,将接收的宽带信号进行分数低阶处理,计算自相关函数,再结合压缩感知原理将分数低阶自相关向量压缩和融合重构,最后经傅立叶变换得到广义功率谱密度。仿真结果表明,该方法具有良好的宽带功率谱密度估计性能,在Alpha稳定分布噪声下能较好地完成宽带频谱感知。

... 传统的频谱感知算法有匹配滤波器检测、能量检测、循环平稳特征检测等方法^[6,7] ...

2010

1.16

0.0

... 通过一系列复杂的数学推导^[8,9],可以得到 H0下香农熵的估计值: ...

2010

0.637

0.0

... 通过一系列复杂的数学推导^[8,9],可以得到 H0下香农熵的估计值: ...

2012

0.0

... 由于 w(n)是独立同分布服从高斯分布的随机变量,因此噪声复频谱的实部和虚部 Wr(k)、Wi(k)也是服从高斯分布的随机变量^[10]: ...

2007

0.0

0.1916

... 指数熵是基于以下原则定义的^[11]: ...