一种新的恒模信号OFDM系统的盲频偏估计算法

引用本文

周游, 朱世磊, 胡捍英. 一种新的恒模信号OFDM系统的盲频偏估计算法. 吉林大学学报:工学版, 2014, 44(5): 1512-1516[ZHOU You, ZHU Shi-lei, HU Han-ying. Novel blind carrier frequency offset estimation algorithm for OFDM systems with constant modulus signaling. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1512-1516] 复制到剪切板

Permissions

一种新的恒模信号OFDM系统的盲频偏估计算法

周游, 朱世磊, 胡捍英

解放军信息工程大学, 郑州 450002

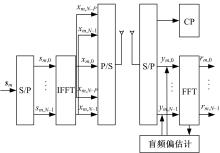
作者简介:周游（1986-）,男,博士研究生.研究方向:无线移动通信.E-mail:emailzhouyou@sina.com

基金:“863”国家高技术研究发展计划项目（2012AA01A502,2012AA01A505）

摘要

载波频偏(CFO)的存在直接影响正交频分复用(OFDM)系统的性能,为了提高CFO的估计精度,提出一种新的适用于恒模信号OFDM系统的盲频偏估计算法。该算法假设连续两个OFDM符号之间的信道变化缓慢,根据相邻OFDM符号各子载波的信号功率差建立代价函数,通过使得代价函数最小化完成CFO的盲估计。通过理论分析获得了该代价函数的闭式解,从而达到有效降低算法复杂度的目的。仿真结果表明:所提算法在高信噪比下与经典算法相比具有较高的估计精度,且对信道阶数变化具有鲁棒性。

关键词: 通信技术; 恒模信号; 正交频分复用; 盲频偏估计; 代价函数; 闭式解

中图分类号:TN929.5 文献标志码:A 文章编号:1671-5497(2014)05-1512-05

Novel blind carrier frequency offset estimation algorithm for OFDM systems with constant modulus signaling

ZHOU You, ZHU Shi-lei, HU Han-ying

PLA Information Engineering University, Zhengzhou 450002, China

Abstract

Carrier Frequency Offset (CFO) has great influence on the performance of OFDM system. In order to improve the accuracy of the CFO estimation, a novel blind CFO estimation algorithm is proposed for OFDM systems with constant modulus signaling. It is assumed that the channel changes slowly in time domain. The cost function based on the difference between signal powers of the two consecutive OFDM symbols in the frequency domain is derived, and the blind CFO estimation is accomplished by minimizing the cost function. Closed form solution to the proposed cost function is given theoretically, which greatly reduces the complexity. Simulation results show the performance of proposed algorithm is better than that of the classical one in high SNR circumstances, and it is robust to the changing order of channel responses.

Keyword: communication technology; constant modulus signaling; orthogonal frequency division multiplexing(OFDM); blind carrier frequency offset estimation; cost function; closed form solution

Show Figures

0 引言

由于正交频分复用(OFDM)具有高传输效率以及抗频率选择性衰落能力而受到广泛关注,已成为新一代宽带移动通信的首选传输方式之一。然而,它对CFO非常敏感,即使较小的CFO也会导致子载波间干扰,严重损害系统的误码率性能^{[ 1]}。为了解决这一问题,已有大量文献对OFDM系统CFO估计进行了相应的研究,主要包括基于数据辅助的CFO估计^{[ 2]}和盲CFO估计^{[ 3]}。

盲CFO估计不需要额外传输辅助数据,节省了系统带宽,近年来成为研究热点。文献[4]提出了一种基于OFDM循环前缀(Cyclic prefix,CP)的CFO估计算法,该算法复杂度较低,但其假设条件过于理想,无法适用于复杂的实际环境。文献[5]利用频率补偿后频域接收数据非高斯性要强于补偿前的特性完成CFO估计,但是其性能受频率选择性衰落的影响较为严重。文献[6]利用子空间的方法完成CFO估计,但是其收敛速度较慢。文献[7]利用过采样以及循环前缀建立盲估计的代价函数,在一定程度上提高了估计精度,但其由于需要对信号进行多倍采样,实现复杂度较高。

本文提出一种新的适用于恒模信号OFDM系统的盲CFO估计算法。算法的基本思路为:假设连续OFDM符号的信道变化缓慢,根据连续对应子载波的功率差建立代价函数,并通过理论推导获得代价函数的闭式解,从而有效降低CFO估计的复杂度。

1 系统模型

子载波数为 $\begin{matrix} N \end{matrix}$ 的OFDM基带系统框图如图1所示,图中省去了成型滤波的部分。

	Figure Option View Download New Window
	图1 OFDM系统框图Fig.1 OFDM system diagram

第 $\begin{matrix} m \end{matrix}$ 组待传输数据用 $\begin{matrix} s_{m} = [s_{m, 0}, s_{m, 1}, \dots, s_{m, N - 1}]^{T} \end{matrix}$ 表示,满足 $\begin{matrix} | s_{i} (m) | = 1 \end{matrix}$ ,即星座图具有恒模特性。IFFT处理后的数据用 $\begin{matrix} x_{m} = [x_{m, 0}, x_{m, 1}, \dots, x_{m, N}]^{T} \end{matrix}$ 表示,添加长度为 $\begin{matrix} P \end{matrix}$ 的CP后经过并串转换发射。用 $\begin{matrix} h_{m} = [h_{m, 0}, h_{m, 1}, \dots, h_{m, L}] \end{matrix}$ 表示频率选择性衰落信道的冲激响应,信道阶数满足 $\begin{matrix} L \leq P 。用 u \end{matrix}$ 表示接收端的CFO估计结果,则经过频率补偿、去除CP以及FFT处理之后的频域数据可以表示为:

$\begin{matrix} r_{m} (u) = e^{j θ_{m, ε}} FΛ (\tilde{ε}) F^{H} H_{m} s_{m} + w_{m} (1) \end{matrix}$

式中: $\begin{matrix} θ_{m, ε} = 2 πε [(m - 1) (N + P) + P] / N \end{matrix}$ 为 $\begin{matrix} ε \end{matrix}$ 在前 $\begin{matrix} m - 1 \end{matrix}$ 个OFDM符号引入的相位误差, $\begin{matrix} \tilde{ε} = ε - u, \end{matrix}$ 表示CFO估计误差,其中 $\begin{matrix} ε \in (- 0.5,0.5] \end{matrix}$ 表示归一化CFO; $\begin{matrix} F \end{matrix}$ 为归一化的FFT矩阵,元素 $\begin{matrix} {[F]}_{mn} = e^{- j 2 πmn / N} / \sqrt[]{N}; Λ_{N} (x) = diag ([1, e^{j 2 πx / N}, \dots, e^{j 2 πx (N - 1) / N}]), \end{matrix}$ 对角矩阵 $\begin{matrix} H_{m} = diag ([H_{m, 0}, H_{m, 1}, \dots, H_{m, N - 1}]^{T}) \end{matrix}$ 表示多径信道频域响应,满足 H_m_, _k= $\begin{matrix} \overset{L}{\sum_{l = 0}} \end{matrix}$ h_m,le^-j2 ^π^kl/N; $\begin{matrix} w_{m} = [w_{m, 0}, w_{m, 1}, \dots, w_{m, N - 1}]^{T} \end{matrix}$ 为零均值的加性高斯白噪声,满足 $\begin{matrix} w_{m} ~ CN (0, σ_{w}^{2} I_{N}), I_{N} \end{matrix}$ 表示维数是 $\begin{matrix} N \times N \end{matrix}$ 的单位矩阵。

2 盲频偏估计算法

2.1 算法原理

从式(1)可以看出,由于估计误差的存在, $\begin{matrix} FΛ (\tilde{ε}) F^{H} \neq I_{N}, \end{matrix}$ 即引入了子载波间干扰。假设估计理想,即 $\begin{matrix} u = ε, \end{matrix}$ 则式(1)可以简化为:

$\begin{matrix} r_{m} (u = ε) = e^{j θ_{ε} (m)} H_{m} s_{m} + w_{m} (2) \end{matrix}$

不考虑噪声,则第 $\begin{matrix} k \end{matrix}$ 个子载波的数据可以表示为:

$\begin{matrix} r_{m, k} (u = ε) = e^{j θ_{m, ε}} H_{m, k} s_{m, k} (3) \end{matrix}$

根据信号的恒模特性,有:

$\begin{matrix} | r_{m, k} (u = ε) |^{2} = | H_{m, k} |^{2} (4) \end{matrix}$

假设信道冲激响应在时域上变化缓慢,则可认为相邻 OFDM符号的对应子载波的冲激响应近似相等,即有:

$\begin{matrix} \begin{matrix} H_{m, k} \approx H_{m + 1, k} (5) \\ 从而有 : \\ | r_{m, k} (u = ε) |^{2} \approx | r_{m + 1, k} (u = ε) |^{2} (6) \end{matrix} \end{matrix}$

从上述分析可以看出,欲提高 CFO的估计精度,尽量减小估计误差,可通过最小化相邻子载波上的信号功率之差实现。因此,定义代价函数如下:

$\begin{matrix} J (u) = \overset{m + M - 1}{\sum_{i = m}} \overset{N - 1}{\sum_{n = 0}} (| r_{i + 1, n} (u) |^{2} - | r_{i, n} (u) |^{2})^{2} (7) \end{matrix}$

其中 $\begin{matrix} (M + 1) \end{matrix}$ 是用于盲频偏估计的连续 OFDM的符号个数。最终估计结果满足:

$\begin{matrix} \hat{ε} = \underset{u \in (- 0.5,0.5]}{argmin} J (u) (8) \end{matrix}$

式(8)可以通过一维搜索的方式求解^{[ 8]},在无限精度的搜索条件下,能够获取 $\begin{matrix} \hat{ε} \end{matrix}$ 的最优解。然而,实际中无法做到无限精度,只能以一定步长进行搜索。如果步长较小,则可以获取较高的估计精度,但是由此带来了较大的计算量;反之,当步长较大时,虽然能够在一定程度上降低计算量,但是估计精度变差,在高信噪比的情况下,还会出现地板效应,即 CFO的估计精度不再随着信噪比的升高而降低。

2.2 闭式解推导

为了便于推导,不妨令 $\begin{matrix} M = 1, \end{matrix}$ 其他情况可通过推广得到。将式(7)展开,有:

$\begin{matrix} \begin{matrix} J (u) = \\ \overset{N - 1}{\sum_{n = 0}} (| r_{m + 1, n} |^{4} + | r_{m, n} |^{4} - 2 | r_{m, n} |^{2} | r_{m + 1, n} |^{2}) (9) \end{matrix} \end{matrix}$

在不致混淆的情况下,式中省略了变量 $\begin{matrix} u, \end{matrix}$ 后面描述中采用相同的方法。

由式(1)可知:

$\begin{matrix} r_{m, n} = \frac{e^{j θ_{m, ε}}}{N} \overset{N - 1}{\sum_{k = 0}} H_{m, k} s_{m, k} \overset{N - 1}{\sum_{i = 0}} e^{j 2 π (\tilde{ε} + k - n) i / N} (10) \end{matrix}$

令 $\begin{matrix} {\tilde{s}}_{m, k} ≜ H_{m, k} s_{m, k}, \end{matrix}$ 则:

$\begin{matrix} \begin{matrix} \overset{N - 1}{\sum_{n = 0}} | r_{m, n} |^{4} = \frac{1}{N^{4}} \overset{N - 1}{\sum_{k_{1}, k_{2}, l_{1}, l_{2} = 0}} {\tilde{s}}_{m, k_{1}} {\tilde{s}}_{m, k_{2}}^{*} {\tilde{s}}_{m, l_{1}} {\tilde{s}}_{m, l_{2}}^{*} \cdot \\ \overset{N - 1}{\sum_{p_{1}, p_{2}, q_{1}, q_{2} = 0}} \exp {j \frac{2 π}{N} [\tilde{ε} (p_{1} - p_{2} + q_{1} - q_{2}) + (k_{1} p_{1} - \\ k_{2} p_{2} + l_{1} q_{1} - l_{2} q_{2}) - n (p_{1} - p_{2} + q_{1} - q_{2})]} (11) \end{matrix} \end{matrix}$

式中: $\begin{matrix} {(\cdot)}^{*} \end{matrix}$ 表示共轭。

令 $\begin{matrix} g ≜ p_{1} - p_{2} + q_{1} - q_{2}, \end{matrix}$ 定义集合 $\begin{matrix} Ω_{0} ≜ {p_{1}, p_{2}, q_{1}, q_{2}} 、 Ω_{1} ≜ {g = 0} 、 Ω_{2} ≜ {g = N} 、 Ω_{3} ≜ {g = - N} 、 Ω_{4} ≜ {g \neq 0, - N, N}, 则有 Ω_{0} = Ω_{1} ⋃ Ω_{2} ⋃ Ω_{3} ⋃ Ω_{4}, 且 Ω_{i} (i = 1, \dots, 4) \end{matrix}$ 两两互斥。令u^(m) $≜ \begin{matrix} \overset{N - 1}{\sum_{n = 0}} \end{matrix}$ |r_m,n|⁴, $\begin{matrix} u_{Ω_{i}}^{(m)} \end{matrix}$ 表示 $\begin{matrix} \overset{N - 1}{\sum_{n = 0}} \end{matrix}$ |r_m,n|⁴取集合 $\begin{matrix} Ω_{i} \end{matrix}$ 中的组合时的数值。容易得知 $\begin{matrix} u_{Ω_{1}}^{(m)} \end{matrix}$ 是与 $\begin{matrix} \tilde{ε} \end{matrix}$ 无关的实数, $\begin{matrix} u_{Ω_{2}}^{(m)} = (u_{Ω_{3}}^{(m)})^{*}, u_{Ω_{4}}^{(m)} = 0 。 \end{matrix}$ 从而式(11)可以化简为:

$\begin{matrix} u_{Ω_{0}}^{(m)} = 2 R (e^{- j 2 π \tilde{ε}} A_{1}^{(m)}) / N^{3} + u_{Ω_{1}}^{(m)} (12) \end{matrix}$

式中: $\begin{matrix} R (\cdot) \end{matrix}$ 表示取实部。

$\begin{matrix} \begin{matrix} A_{1}^{(m)} = \overset{N - 1}{\sum_{k_{1}, k_{2}, l_{1}, l_{2} = 0}} {\tilde{s}}_{m, k_{1}} {\tilde{s}}_{m, k_{2}}^{*} {\tilde{s}}_{m, l_{1}} {\tilde{s}}_{m, l_{2}}^{*} \cdot \\ \overset{N - 1}{\sum_{p_{1} = 0}} \overset{N - 1}{\sum_{p_{2} = p_{1} + 1}} \overset{p_{2} - p_{1} - 1}{\sum_{q_{1} = 0}} e^{j 2 π \frac{(k_{1} - l_{2}) p_{1}}{N}} e^{- j 2 π \frac{(k_{2} - l_{2}) p_{2}}{N}} e^{j 2 π \frac{(l_{1} - l_{2}) q_{1}}{N}} (13) \end{matrix} \end{matrix}$

同理,令v^(m) $≜ \begin{matrix} \overset{N - 1}{\sum_{n = 0}} \end{matrix}$ |r_m,n|²|r_m+1,n|²也可得到类似的结论,有:

$\begin{matrix} \begin{matrix} v_{Ω_{0}}^{(m)} = 2 R (e^{- j 2 π \tilde{ε}} A_{2}^{(m)}) / N^{3} + u_{Ω_{1}}^{(m)} (14) \\ 其中 : \\ A_{2}^{(m)} = \overset{N - 1}{\sum_{k_{1}, k_{2}, l_{1}, l_{2} = 0}} {\tilde{s}}_{m, k_{1}} {\tilde{s}}_{m, k_{2}}^{*} {\tilde{s}}_{m + 1, l_{1}} {\tilde{s}}_{m + 1, l_{2}}^{*} \cdot \\ \overset{N - 1}{\sum_{p_{1} = 0}} \overset{N - 1}{\sum_{p_{2} = p_{1} + 1}} \overset{p_{2} - p_{1} - 1}{\sum_{q_{1} = 0}} e^{j 2 π \frac{(k_{1} - l_{2}) p_{1}}{N}} e^{- j 2 π \frac{(k_{2} - l_{2}) p_{2}}{N}} e^{j 2 π \frac{(l_{1} - l_{2}) q_{1}}{N}} (15) \end{matrix} \end{matrix}$

定义集合 $\begin{matrix} Θ_{0} ≜ {k_{1}, k_{2}, l_{1}, l_{2}} 、 Θ_{1} ≜ {k_{1} = k_{2}, l_{1} = l_{2}} 、 Θ_{2} ≜ {k_{1} = k_{2}, l_{1} \neq l_{2}} 、 Θ_{3} ≜ {k_{1} \neq k_{2}, l_{1} = l_{2}} 、 Θ_{4} ≜ {k_{1} \neq k_{2}, l_{1} \neq l_{2}} 、且 Θ_{i} (i = 1, \dots, 4) \end{matrix}$ 两两互斥,从而有:

$\begin{matrix} \{\begin{matrix} A_{1}^{(m)} = A_{1, Θ_{1}}^{(m)} + A_{1, Θ_{2}}^{(m)} + A_{1, Θ_{3}}^{(m)} + A_{1, Θ_{4}}^{(m)} \\ A_{1}^{(m + 1)} = A_{1, Θ_{1}}^{(m + 1)} + A_{1, Θ_{2}}^{(m + 1)} + A_{1, Θ_{3}}^{(m + 1)} + A_{1, Θ_{4}}^{(m + 1)} \\ A_{2}^{(m)} = A_{2, Θ_{1}}^{(m)} + A_{2, Θ_{2}}^{(m)} + A_{2, Θ_{3}}^{(m)} + A_{2, Θ_{4}}^{(m)} \end{matrix} (16) \end{matrix}$

在式(5)的假设条件下,有:

$\begin{matrix} \{\begin{matrix} A_{1, Θ_{1}}^{(m)} \approx A_{1, Θ_{1}}^{(m + 1)} \approx A_{2, Θ_{1}}^{(m)} \\ A_{1, Θ_{2}}^{(m)} = A_{3, Θ_{3}}^{(m)} \approx A_{2, Θ_{3}}^{(m)} \\ A_{1, Θ_{2}}^{(m + 1)} \approx A_{1, Θ_{3}}^{(m + 1)} \approx A_{2, Θ_{2}}^{(m)} \end{matrix} (17) \end{matrix}$

在集合 $\begin{matrix} Θ_{4} \end{matrix}$ 中,由 $\begin{matrix} k_{1} \end{matrix}$ 和 $\begin{matrix} k_{2} \end{matrix}$ 以及 $\begin{matrix} l_{1} \end{matrix}$ 和 $\begin{matrix} l_{2} \end{matrix}$ 的对称性容易得知, $\begin{matrix} A_{1, Θ_{4}}^{(m)} 、 A_{1, Θ_{4}}^{(m + 1)} \end{matrix}$ 以及 $\begin{matrix} A_{2, Θ_{4}}^{(m)} \end{matrix}$ 都是实数,且满足:

$\begin{matrix} A_{1, Θ_{4}}^{(m)} + A_{1, Θ_{4}}^{(m + 1)} - 2 A_{2, Θ_{4}}^{(m)} < 0 (18) \end{matrix}$

将式(14)代入式(9),并利用式(16) ~(18)可得:

$\begin{matrix} \begin{matrix} J (u) \approx A^{(m)} \cos [2 π (ε - u)] + B^{(m)} (19) \\ 式中 : \\ \{\begin{matrix} A^{(m)} = 2 (A_{1, Θ_{4}}^{(m)} + A_{1, Θ_{4}}^{(m + 1)} - 2 A_{2, Θ_{4}}^{(m)}) / N^{3} \\ B^{(m)} = u_{Ω_{1}}^{(m)} + u_{Ω_{1}}^{(m + 1)} - 2 v_{Ω_{1}}^{(m)} \end{matrix} (20) \end{matrix} \end{matrix}$

不难看出, $\begin{matrix} A^{(m)} \end{matrix}$ 和 $\begin{matrix} B^{(m)} \end{matrix}$ 与 $\begin{matrix} ε \end{matrix}$ 以及 $\begin{matrix} u \end{matrix}$ 无关。当发射数据以及信道一定时, $\begin{matrix} A^{(m)} \end{matrix}$ 和 $\begin{matrix} B^{(m)} \end{matrix}$ 的值是固定的。当 $\begin{matrix} u = ε \end{matrix}$ 时, $\begin{matrix} J (u) \end{matrix}$ 取到最小值,进一步说明了代价函数的合理性。

上面给出了当 $\begin{matrix} M = 1 \end{matrix}$ 时的代价函数闭式解,当 $\begin{matrix} M > 1 \end{matrix}$ 时,式(19)变为:

$\begin{matrix} J (u) \approx Acos [2 π (ε - u)] + B (21) \end{matrix}$

式中:A= $\begin{matrix} \overset{m + M - 1}{\sum_{i = m}} \end{matrix}$ A⁽ⁱ⁾;B= $\begin{matrix} \overset{m + M - 1}{\sum_{i = m}} \end{matrix}$ B⁽ⁱ⁾。

综上所述,式(21)即为本文所设代价函数的闭式解,至此推导过程结束。

2.3 算法描述

通过式(21)可以看出,其仅有 $\begin{matrix} A 、 B \end{matrix}$ 以及 $\begin{matrix} ε \end{matrix}$ 三个未知量,因此仅试验3个 $\begin{matrix} u \end{matrix}$ 值就可以求解出 $\begin{matrix} \hat{ε} 。 \end{matrix}$ 本文选择 $\begin{matrix} u = - 1 / 4 、 u = 0 \end{matrix}$ 以及 $\begin{matrix} u = 1 / 4, \end{matrix}$ 则有:

$\begin{matrix} \{\begin{matrix} J (- 1 / 4) = - Asin [2 πε] + B \\ J (0) = - Acos [2 πε] + B \\ J (1 / 4) = - Asin [2 πε] + B \end{matrix} (22) \end{matrix}$

当 $\begin{matrix} A < 0 \end{matrix}$ 时,令 $\begin{matrix} a ≜ [J (1 / 4) + J (- 1 / 4)] / 2 - J (0); b ≜ [J (- 1 / 4) - J (1 / 4)] / 2, \end{matrix}$ 则估计值 $\begin{matrix} \hat{ε} \end{matrix}$ 可按下式获取:

$\begin{matrix} \hat{ε} = \{\begin{matrix} \arctan (b / a) / (2 π), a \geq 0 \\ [\arctan (b / a) + π] / (2 π), a < 0, b \geq 0 \\ [\arctan (b / a) - π] / (2 π), a < 0, b < 0 \end{matrix} (23) \end{matrix}$

基于上述分析,本文所提算法的步骤可以简述如下:

Step1 先分别用 $\begin{matrix} u = - 1 / 4 、 u = 0 \end{matrix}$ 以及 $\begin{matrix} u = 1 / 4 \end{matrix}$ 对接收数据完成频偏补偿,并分别计算式(7)的值。

Step2 根据式(23)完成 CFO的估计。

值得注意的是,当系统中有虚拟子载波存在时, $\begin{matrix} J (u) \end{matrix}$ 需要改写为:

$\begin{matrix} \begin{matrix} J (u) = \\ \overset{M - 1}{\sum_{m = 0}} \overset{k_{0} + D - 1}{\sum_{k = k_{0}}} (| r_{m + 1, k} (u = ε) |^{2} - | r_{m, k} (u = ε) |^{2})^{2} (24) \end{matrix} \end{matrix}$

式中: $\begin{matrix} k_{0} \end{matrix}$ 为承载数据的起始子载波的序号; $\begin{matrix} D \end{matrix}$ 为承载数据的子载波个数。

此时,式(17)(18)仍然近似成立,所以式(21)的结论也近似成立。但与一维搜索相比,此时性能会略有损失,这一点也可以从后文的仿真中得到进一步的验证。

3 仿真结果

为了分析算法性能,本文针对所提算法以及文献[5]算法进行了性能差异的仿真。仿真环境除非特殊说明,否则 $\begin{matrix} M = 1, D = 64, N = 64, P = 16, L = 8, k_{0} = 0; \end{matrix}$ 信道抽头系数 $\begin{matrix} h_{m, l} \end{matrix}$ 独立同分布,且满足 $\begin{matrix} h_{m, l} ~ CN (0, σ_{l}^{2}), σ_{l}^{2} = a e^{- l / 10}, l = 0, \dots, L, 其中的 a \end{matrix}$ 是使抽头系数功率归一化的因子^{[ 9]}; $\begin{matrix} ε \end{matrix}$ 在( -0 .5,0 .5]范围内以0 .001为间隔均匀分布;数据符号采用 QPSK调制。

利用归一化的均方误差对算法性能进行评价:

$\begin{matrix} NMSE = \overset{N_{m}}{\sum_{i = 1}} \frac{{(ε - \hat{ε})}^{2}}{N_{m} ε^{2}} (25) \end{matrix}$

式中: $\begin{matrix} N_{m} \end{matrix}$ 为仿真次数,仿真中 $\begin{matrix} N_{m} = 500 。 \end{matrix}$

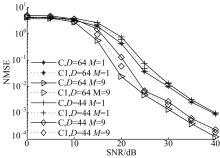
为对算法性能进行对比,噪声方差 $\begin{matrix} σ_{w}^{2} \end{matrix}$ 与信噪比 SNR之间的关系表示为:

$\begin{matrix} SNR = 10 \lg \frac{D}{(N + P) σ_{w}^{2}} (26) \end{matrix}$

仿真1 本文算法通过一维搜索和闭式解进行 CFO估计的性能仿真结果如图2所示。“ C1”表示一维搜索的结果,“ C”表示闭式解的结果。为了保证一维搜索过程中始终能够试验真实的频偏值,步进选择为0 .001。图中分别对比了虚拟子载波数为0和20、 $\begin{matrix} M \end{matrix}$ 为1和9时的算法性能。从图中可以看出,当虚拟子载波数为0时,一维搜索和闭式解的估计结果几乎重合;当虚拟子载波数为20时,闭式解的估计性能略有损失。进一步说明了可以用推导得到的闭式解代替一维搜索。另外,当用于估计的 OFDM符号数从2个增加到10个时,所提算法性能得到提升。之后的仿真中,系统中均假设不存在虚拟子载波,且算法采用闭式解估计的结果。

	Figure Option View Download New Window
	图2 一维搜索和闭式解性能对比Fig.2 Performance comparison between 1-D search and closed-form solution

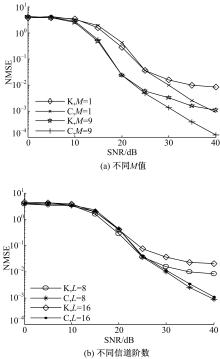
仿真2 本文算法与文献[5]算法性能对比的仿真结果如图3所示。“ K”表示文献[5]算法的结果。仿真过程中,文献[5]算法采用一维搜索的方式进行估计。图3( a)给出了两种算法在不同 OFDM符号个数下的性能。从图中可以看出,在数据子载波个数以及用于估计的 OFDM符号个数相同的情况下,低信噪比时两种算法性能相当,而在高信噪比时本文算法均远优于文献[5]的算法。

	Figure Option View Download New Window
	图3 本文算法与文献[5]算法性能对比Fig.3 Performance comparison between proposed algorithm and the algorithm in [5]

图3( b)给出了两种算法在不同信道阶数下的性能。从图中可以看出,文献[5]算法性能受信道阶数影响较大,而本文算法受其影响较小。主要是由于本文算法利用了连续 OFDM符号经过的信道变化缓慢的特点,只要信道阶数未超出 CP长度,对算法性能的影响不大。文献[5]利用的是频率补偿后 FFT输出数据高斯特性要弱于补偿前的特性,当信道阶数增加时,补偿后的 FFT输出数据的高斯特性会增强,代价函数的检测性能变差,导致性能下降。

4 结束语

针对恒模信号 OFDM系统提出一种新的盲频偏估计算法,并给出了算法的闭式解,大大降低了算法的复杂度。仿真表明了闭式解的正确性,算法性能随着用于估计的 OFDM符号个数的增

加而提升;与经典算法相比,算法在高信噪比下具有较大的性能优势,且对信道阶数的变化具有鲁棒性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Pollet T, Van Bladel M, Moeneclaey M. BER sensitivity of OFDM systems to carrier frequency offset and Wiener phase noise[J]. IEEE Transactions on Communications, 1995, 43(24): 191-193 [本文引用:1] [JCR: 1.75]
[2]	Yu J, Su Y. Pilot-assisted maximum-likelihood frequency-offset estimation for OFDM systems[J]. IEEE Transactions on Communications, 2004, 52(11): 1997-2008 [本文引用:1] [JCR: 1.75]
[3]	Pantos G D. A numerical technique for blind estimation of carrier frequency offset in OFDM systems[J]. IEEE Transactions on Broadcasting, 2009, 52(4): 566-569 [本文引用:1] [JCR: 2.087]
[4]	Lashkarian N, Kiaei S. Class of cyclic-based estimators for frequency offset estimations of OFDM systems[J]. IEEE Transactions on Communications, 2006, 52(2): 236-244 [本文引用:1] [JCR: 1.75]
[5]	Yao Y, Giannakis G B. Blind carrier frequency offset estimation in SISO, MIMO, and multiuser OFDM systems[J]. IEEE Transactions on Communications, 2005, 53(1): 173-183 [本文引用:1] [JCR: 1.75]
[6]	Zhang W L, Gao F F, Yin Q Y, et al. Blind carrier frequency offset estimation for interleaved OFDMA uplink[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3616-3627 [本文引用:1] [JCR: 2.813]
[7]	Jeon H G, Kim K S, Serpedin E. An efficient blind deterministic frequency offset estimator for OFDM systems[J]. IEEE Transactions on Communications, 2011, 59(4): 1133-1141 [本文引用:1] [JCR: 1.75]
[8]	Sun P F, Zhang L. Low complexity pilot aided frequency synchronization for OFDMA uplink transmission[J]. IEEE Transactions on Wireless Communications, 2009, 8(7): 3758-3769 [本文引用:1] [JCR: 2.418]
[9]	Huang W C, Pan C H, Li C P, et al. Subspace-based semi-blind channel estimation in uplink OFDMA systems[J]. IEEE Transactions on Broadcasting, 2010, 56(1): 58-65 [本文引用:1] [JCR: 2.087]